Quickfur's renders

[mr_e_man]

On your Uniform Polyhedra page, the "portrait" description is missing the 20-gon prism in the 2nd row.

Haha, I'm not particularly inclined to add it, since there are an infinite number of prisms, and the ones shown are just a few selected ones.

I mean the description doesn't match the picture. The 20-gon prism is in the picture, but it's not in the description.

[mr_e_man]

viewtopic.php?p=19492#p19492

In the past few days I kinda got back into dabbling with 4D stuff -- considering how to represent polytope cell complexes as a way of interactively finding 4D CRFs by hand ("4D lego", if you will). Found some interesting theorems; but I'll have to post about that another time.

Have you posted that anywhere yet? (Or, do you even remember what you were talking about then?)


viewtopic.php?p=26001#p26001

Also, when coloring a very large polytope, often the surtope subset that needs coloring contains elements that are touching each other, so individual elements have to be assigned different colors. The program currently has no automation for this, so I end up having to solve the graph coloring problem by hand over and over, once per subset of cells to color.

You could add a slight random variation to the colours, so that different cells look different, but still similar enough if they're in the same subset.


viewtopic.php?p=26132#p26132

Nothing new here, but this is the last of the known scaliform polychora on my website, so it seems like a natural thing to follow after spidrox.

Actually, there's one more convex scaliform polytope you haven't posted yet - tutcup (truncated tetrahedral cupolipirsm), which has 2 truncated tetrahedra, 6 tetrahedra, and 8 triangular cupolae. It is a segmentotope whose bases are two oppositely oriented truncated tetrahedra.

Ooh! Thanks for the tip! I'll be sure to post that next month!

Are all of the convex scaliforms already known? Or are these only the currently-known ones?

Definitely yes in 4D. They are related to a specific convex uniform polychoron (ex. tutcup-sircope, bidex-ex, and prissi-prico).

Not sure I understand. Are you saying we know all of them, or these are the only ones we know of? If the former, do we have proof that there are no others?

I also want an answer to this. I didn't find anything on Klitzing's site saying that all 4D convex scaliforms have been found. (Surely not all 4D scaliforms have been found, as the search for 4D non-convex uniforms is on-going.)

[Klitzing]

viewtopic.php?p=26132#p26132

Nothing new here, but this is the last of the known scaliform polychora on my website, so it seems like a natural thing to follow after spidrox.

Actually, there's one more convex scaliform polytope you haven't posted yet - tutcup (truncated tetrahedral cupolipirsm), which has 2 truncated tetrahedra, 6 tetrahedra, and 8 triangular cupolae. It is a segmentotope whose bases are two oppositely oriented truncated tetrahedra.

Ooh! Thanks for the tip! I'll be sure to post that next month!

Are all of the convex scaliforms already known? Or are these only the currently-known ones?

Definitely yes in 4D. They are related to a specific convex uniform polychoron (ex. tutcup-sircope, bidex-ex, and prissi-prico).

Not sure I understand. Are you saying we know all of them, or these are the only ones we know of? If the former, do we have proof that there are no others?

I also want an answer to this. I didn't find anything on Klitzing's site saying that all 4D convex scaliforms have been found. (Surely not all 4D scaliforms have been found, as the search for 4D non-convex uniforms is on-going.)

No proof is known to me either. Wrt. the convex polychora it is. For the non-convex ones the search obviously is on-going.
--- rk

[quickfur]

I've been meaning to do this, but haven't gotten to around to it until now: my website has moved. The website itself hasn't changed, but I've switched to a different domain name: https://www.qfbox.info/4d/. The old domain name will remain active until next year, then it will be permanently deleted. Please update your bookmarks! All URL paths remain the same, except for the hostname. So it shouldn't be too hard to update any existing bookmarks/links you have. (In theory, anyway. )

[username5243]

I've been meaning to do this, but haven't gotten to around to it until now: my website has moved. The website itself hasn't changed, but I've switched to a different domain name: https://www.qfbox.info/4d/. The old domain name will remain active until next year, then it will be permanently deleted. Please update your bookmarks! All URL paths remain the same, except for the hostname. So it shouldn't be too hard to update any existing bookmarks/links you have. (In theory, anyway. )

Someone on the Polytope Wiki already seems to have changed it a while ago. I let Klitzing know elsewhere and all his links should be fixed whenever he next updates. I let Bowers know too so he hopefully will when he updates in the near future (we've been doing a lot of non-convex searching lately, he's got a lot of things to update). I can't think of any other links that need updated...

[quickfur]

It's been a while, but I finally got around to updating my website again. I'm starting the Catalan project -- to cover all the Catalans: 3D first, then the dual prisms and antiprisms, then the 4D catalans. Starting out small, with the relatively small triakis tetrahedron:



I actually already have the next 3 Catalans lined up, but will post only one per month to give myself enough buffer to keep things going. Hopefully I'll be able to keep going until I finish the 4D catalans!

[quickfur]

Don't know if anybody still follows this thread, but I've posted the next Catalan solid on my website:



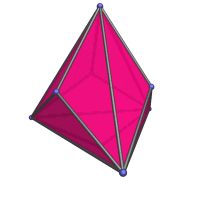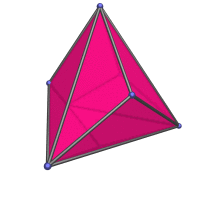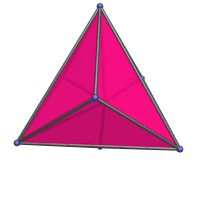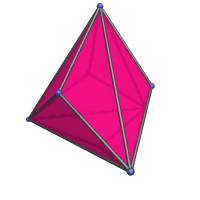
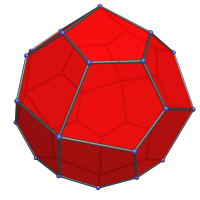
This is, of course, the rhombic dodecahedron, which everybody here should already know about. But it's nice to finally have an actual page to link to in the various mentions of the rhombic dodecahedron, like in the projection of the tesseract and the 24-cell.

That, and also I'm using these relatively simple 3D catalans as buffer to work on the pages for the 4D catalans. Well, relatively simple except for the pentagonal icositetrahedron (dual of the snub cube), which needed a bit of work to wrangle with due to the cubic equations involved, and the pentagonal hexecontahedron (dual of the snub dodecahedron), which gave me a big headache for maybe a week or two because it involves 12th degree polynomials (square roots of cubics involving the golden ratio). I'm still not 100% sure I've completely picked it apart yet, but at least I've figured out enough to have algebraic expressions for its coordinates and edge length ratios. The pages for all the catalans are in fact already ready, I'm just publishing them one per month.

I'm also doing the duals of uniform prisms and antiprisms, and already one of them will definitely feature as cells in one of the 4D catalans, with at least another one that I suspect will also be cells to another 4D catalan.

[Mecejide]

Will you ever do nonconvex stuff?

[quickfur]

Will you ever do nonconvex stuff?

I would, if I could find a simple way to construct them. Currently all of the polytopes on my website are made from specifying vertices or hyperplanes and passing them through a convex hull algorithm followed by a face lattice enumeration algorithm that creates the entire structure automatically. But for non-convex stuff a convex hull algorithm obviously wouldn't work. But without that it would be too tedious to construct the face lattice by hand (esp. for the 600-cell family polytopes, which have a large number of elements). For symmetrical polytopes I suppose I could just do faceting... but still, currently I don't really have a good solution for constructing these things in a way that doesn't involve tons of error-prone manual work.

[Klitzing]

There is a free polytope software miratope (https://github.com/galoomba1/miratope-rs), which allows to generate the full element structure of a given polytope and even allows to facet a given polytope. In fact it was set up (and there even can be joined to further code it) by members of the polytope discord.

--- rk

[mr_e_man]

I generally dislike non-convex polytopes, because we can't even agree on what they are! There are many different definitions, and many different ways to render them, even in 3D.

[quickfur]

I generally dislike non-convex polytopes, because we can't even agree on what they are! There are many different definitions, and many different ways to render them, even in 3D.

Reminds me of Grünbaum's Are Your Polyhedra the Same as My Polyhedra?. I think eventually this boils down to the divide between abstract polyhedra (polytopes) vs actual realizations of them as concrete polyhedra that exist in some kind of ambient space (be it euclidean, hyperbolic, spherical, or I dunno, parabolic or projective). A concrete polyhedron (polytope) always has an associated abstract polyhedron (polytope), but the reverse may not always be true (some abstract polytopes may be impossible to realize faithfully in any kind of space, e.g., Coxeter's 11-cell). Sorta reminds me of the split between ordinals and cardinals in set theory. As long as you stay within the realm of the finite (resp. convex) the two remain equivalent. But once you step out into the realm of the infinite (resp. nonconvex) the two become inherently, irreconcilibly different, and their relationship with each other becomes complicated. And "monsters" like the Cantor set appear (resp. Bowers' "wild" polychora, with fissary / degenerate / etc. cases -- or for that matter, the 11-cell and other such things that can't be faithfully realized in any space).

[quickfur]

This month's polytope is the tetrakis hexahedron, dual of the truncated octahedron:



It's also the projection envelope of the vertex-first perspective projection of the 24-cell into 3D.

I actually already have one of the 4D catalans rendered and ready, but decided to give myself a bit more time to polish it before posting it publicly. Probably will do it next month.

[mr_e_man]

Your Catalan pages don't mention some nice properties that follow from duality:

• All vertex figures are regular polygons.
• All 2-dyad (dihedral) angles are equal.
• All 1-dyad angles around a given vertex are equal.

The tetrakis cube could be constructed directly (not dually), by erecting pyramids on the cube's faces, and varying the height of the pyramids until all dihedral angles are equal.

[quickfur]

Your Catalan pages don't mention some nice properties that follow from duality:

• All vertex figures are regular polygons.
• All 2-dyad (dihedral) angles are equal.
• All 1-dyad angles around a given vertex are equal.

Added, thanks!

The tetrakis cube could be constructed directly (not dually), by erecting pyramids on the cube's faces, and varying the height of the pyramids until all dihedral angles are equal.

Nice!

[quickfur]

Already posted this on my website 10 days ago, but only just gotten around to posting it here:



This is the joined bidecachoron, the first 4D Catalan on my website. Relatively simple, but has nice connections with 3D Catalans.

[mr_e_man]

Your Catalan pages don't mention some nice properties that follow from duality:

• All vertex figures are regular polygons. [But this depends on the definition of vertex figures.]
• All 2-dyad (dihedral) angles are equal.
• All 1-dyad angles around a given vertex are equal.

Similarly, for the Catalan polychora:

• All 3-dyad (dichoral) angles are equal.
• All 2-dyad angles around a given edge are equal.

[quickfur]

Done, thanks for the info!

[mr_e_man]

Ahh, that's not quite right:

Being the duals of the uniform polychora confers these polytopes the following properties:

• They are cell-transitive;
• All dichoral angles are equal;
• All dihedral angles around each edge are equal;
• The angles between adjacent edges around a vertex are all equal.

Sorry if my previous (March 6) post wasn't clear; it applies only to 3D, not higher dimensions. In a 4D Catalan, the 1-dyad angles around a vertex may be unequal.

These properties of uniform N-polytopes and Catalan N-polytopes are related by duality.

• Uniform: All 0-dimensional elements (vertices) are equivalent by symmetry. Catalan: All (N-1)-dimensional elements are equivalent by symmetry.
• Uniform: All 0-dyads (edges) are congruent. Catalan: All (N-1)-dyads are congruent.
• Uniform: All 1-dyads contained in a given 2-dimensional element (angles in a given face) are congruent. Catalan: All (N-2)-dyads containing a given (N-3)-dimensional element are congruent.

(In fact this also applies to scaliforms and their duals. In addition to scaliformity, uniform N-polytopes have uniform [-1, N-1]-subpolytopes. But I'm less sure about the duality here, because the subpolytopes are off-centre. If the duality still applies, Catalan N-polytopes should have Catalan [0, N]-subpolytopes (i.e. vertex figures).)

[wendy]

the catalans are duals of the uniforms.

Face transitive face in solid-1 or s-1 d
single margin angle. angle over surtope s-2

After the tegum products, and the polygonal antiregums, there are the wythoff mirror margins, and a few scattered others

[username5243]

Already posted this on my website 10 days ago, but only just gotten around to posting it here:



This is the joined bidecachoron, the first 4D Catalan on my website. Relatively simple, but has nice connections with 3D Catalans.

I think the name here should be joined pentachoron (or joined 5-cell, if you prefer), since that is what it is based on and there are no decachoric symmetries in the thing. Am looking forward to whatever you have next (even if it's only back to 3D).

[wendy]

join means too many things. The thing looks like a surtegmated pentochoron. it is the dual of E4, and the 4d elements of the E8 voroni cells.

[quickfur]

Yall probably already saw this, but just in case:



This is this month's Polytope of the Month: the deltoidal icositetrahedron, the dual of the rhombicuboctahedron. Just a boring ole 3D object, but nevertheless interesting in its own right IMO.

[quickfur]

Here's the next one:



This is the triakis octahedron, dual of the truncated cube. Not much to say here, other than that it's a pretty little Catalan solid.

I haven't had much time to work on the 4D Catalans, so filling in with the 3D ones for now. Hopefully I'll get enough 4D Catalans into my buffer before I run out of the 3D ones!

[quickfur]

I'm burning through my buffer of 3D Catalans, but haven't even started on the next 4D one yet. But anyway, here's this month's:



This is the disdyakis dodecahedron, the dual of the great rhombicuboctahedron (x4x3x). Well, you guys should already know what it is.

[quickfur]

This month I decided to wrap up the cube/octahedron family of Catalans. The last entry is:



the pentagonal icositetrahedron, the dual of the snub cube. Well, you guys already all know that, so I won't bother repeating myself.

This month I actually made some progress on the 4D Catalans: another two are almost ready to be shown to the world. They're sitting in my queue, but just need a little bit more polish before I publish them. Most likely this will happen starting next month -- I'm planning to post them over the course of 2-3 months, so stay tuned! They will be from the tesseract and 24-cell families.

[mr_e_man]

24 scalene pentagons

I've never seen a definition of "scalene" for anything other than triangles.
(...Now I've seen "scalene ellipsoid". Still nothing for polygons.)

Something with no symmetry can be called "asymmetric". Something with only rotation symmetry can be called "chiral". A polygon with no edge lengths equal, I suppose, can be called "scalene". All of these are generalizations of triangle scalenity. (But none of them apply to those 24 pentagons.)

"Isosceles" also is rarely defined for larger polygons, but the obvious meaning is that it has mirror symmetry. https://lexique.netmath.ca/en/isosceles-polygon/

[quickfur]

lol, existing terminology seems very much biased towards triangles. I just chose "scalene" to mean non-regular. Maybe I should just use "non-regular" instead? "Irregular" seems to imply all lengths unequal or having no symmetry at all, but we do have mirror symmetry here. So I don't know.

[Klitzing]

how about "only mirror symmetric"?
perhaps further adding "equilateral"?

--- rk

[quickfur]

Equilateral seems to imply that all edge lengths are equal, which is not the case here.

Anyway, lacking a better word, I changed it to "non-regular". It will have to do for now until I think of something better.