
Below is a table showing the relation between the dimensions:
| person | dimension | view | axis of rotation |
|---|---|---|---|
| --- | 1st | point(0D) | *no rotation* |
| Fred | 2nd | line(1D) | point(0D) |
| Bob | 3rd | plane(2D) | line(1D) |
| Emily | 4th | realm(3D) | plane(2D) |
I'm now going to describe in more detail the worlds of Fred, Bob, and Emily. Fred doesn't actually have much of an area to live in. His little 2D plane is actually hanging on the wall of Bob's living room. Bob can walk over and observe Fred any time he likes. Fred's world has a ceiling, a front, a back, and a floor. Bob's world, actually, isn't very big either. He has a ceiling, 4 walls, and a floor. His 3-D world is also hanging on a wall: in Emily's living room. Emily's world could also be hanging on someone else's wall, and so on. Here is Fred's world on Bob's wall:

If a square is rotated in fred's world, it rotates around a single point. This means that only a single point on the square stays at its original location as the square spins around. Thus, the axis of an object in planespace is zero-dimensional.
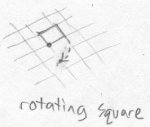
Now imagine that Bob has Fred's world resting flat on a table. Bob has placed a cube on Fred's 2d world, as if the cube is a paperweight to hold down Fred's world from fluttering away in the wind. Fred's world is sandwiched between the table and the cube paperweight. The bottom surface of the cube, which is intersected with Fred's world, appears to Fred to be a simple square. If this cube is rotated, it appears to Fred as though a square is rotating around a point. In reality, it is a cube rotating around a line, whose axis extends perpendicular to Fred's world from the point of rotation. This means that all of the points along the axis will stay at their original location as the cube spins, but every other point in the cube will move in a circle. Thus, the axis of an object in realmspace is one-dimensional.

Now imagine that Emily lays Bob's world flat on a tetral table. The direction towards the table from Bob's world is delta (down in tetraspace), and the opposite direction into the air above the table is upsilon (up in tetraspace). Emily places a tetracube on top of Bob's world on the upsilon side of it. Bob's world is now sandwiched between the tetral table and the tetracube. The tetracube is intersected with Bob's world, so Bob sees a cube floating in mid-air. Now let's say that Emily rotates her tetracube around one of it's edges. Bob will only see a cube rotating, but the tetracube it's attached to is rotating with it. The axis of rotation for the tetracube isn't a line, though. It's a plane formed by extending the linear edge of the cube into Emily's world, perpendicular to realmspace. All of the points on this square stay in place as the tetracube rotates in tetraspace. Thus, the axis of an object in tetraspace is two-dimensional.
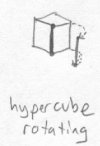
Imagining how the linear axis of a cube could extend into tetraspace is hard. We can try to picture it by imagining its axis shifting off in a random direction as pictured below, even though this isn't what is truly happening:
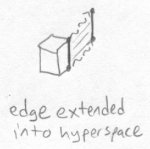
Fred is sitting in his living room the next day, and there is a square object floating in front of him in mid-air. Bob decides to play a trick on Fred. He grabs an edge of the square and pulls it into realmspace, leaving a linear edge in Fred's universe remaining. Fred only sees a line left of the original square. Here is what Bob just did:

Bob completes the rotation and places the square fully back into Fred's world. But, now the edge that had disappeared is on the opposite side. Fred is now astonished to see that the square has been completely inverted. Such an action would be impossible in a two dimensional world. Fred tries to invert the square back to its normal state, but no matter how many times he turns the square around, it doesn't work:
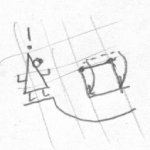
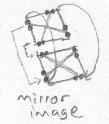
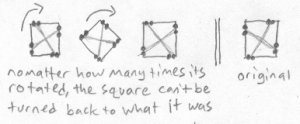
The square has become its mirror image, with its left and right sides swapped. Fred has difficulty understanding how this could have happened to his square. The first way he tries to imagine it is to imagine that one of the sides has been pushed through the middle of the square and to the opposite side, making everything inverted. This is how he imagines it:
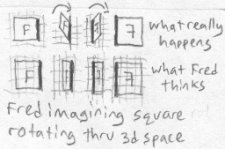
Fred contemplates what happened some more, but can't quite wrap his mind around it. He thinks about another way it might have happened. One side could have been shifted upwards and towards the other one until one side was above the other, then shifted further until it came into place on the other side. The moved side would have made a half circle around the side that stayed. Here is how he imagines it this time:
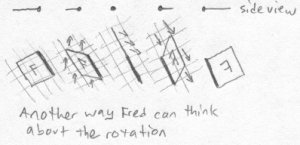
But, this is not what really happened. It is merely a futile attempt of Fred's to understand what's happened in the third dimension using only what he knows of the second dimension. The effects of Bob's actions are easy to see, but explaining them to Fred is not.
Emily sees what Bob did to Fred, and decides to play a similar trick on him. Bob is sitting on his floor staring at a box that he has just filled with his favorite sentimental possessions, when all of a sudden the whole box except one of its sides disappears. Here is what he sees:
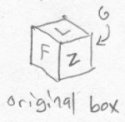
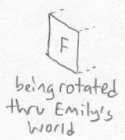
He stares at it astonished, and is even more surprised when all of a sudden the rest of the box appears again. But, the box has just appeared on the opposite side of the face that had remained. All of the lettering on the box has been turned into its mirror image. Here is what the box looks like afterwards:

Bob looks into the box, and finds that something has happened to all the letters in the books that were in the box - they are all their mirror images! He takes one of the books and puts it up to a mirror, and finds that the mirror reverses the letters back to their original state. As Fred did, Bob tries to understand how this could possibly occur. He tries to imagine one side of the box being squished into its opposite side, but being pushed further until it comes into place on the other side of the box from where it was before. All of the letters have been inversed:
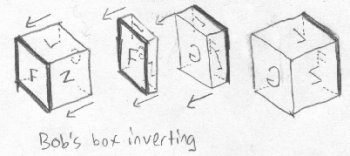
This is analogous to Fred's solution with the disappearing side being squished through the remaining side. It isn't what really happened in tetraspace, though. Bob contemplates further, and again conceives of another idea like Fred did. Maybe one face of the box was shifted in a half circle around the side that remained. All the letters would end up being reversed just like in the previous theory:

As we know by looking at Fred's example, the size and shape of the square don't actually change as it's rotated through realmspace. The only ways that Fred has thought of to explain what happened involve the square changing shape. The real event doesn't require the square to change shape at all. It is the same situation with the cube. As it is rotated through tetraspace, the actual shape of it isn't changed at all; it remains a perfect cube. The only way we can imagine the result, however, is by distortions in realmspace.