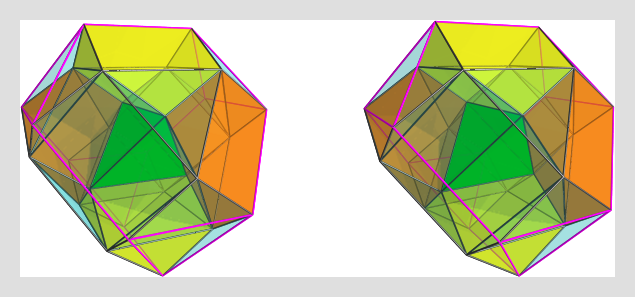
The green tetrahedron is the top cell of this CRF, and the antipodal truncated tetrahedron is outlined in magenta edges. Most importantly, you can see 2 of the 3 pairs of gyrobifastigium (J26) cells sharing edges with the central tetrahedron. The other pair is not shown because it would clutter the image too much.
Here they are, shown separately:

You can easily spot the octahedral cells at the 4 corners of the tetrahedral-like projection envelope, as well as the 4 tetrahedra touching the central one. The triangular face opposite the shared vertices are where these tetrahedra join with the trigonal cupolae that link them to the antipodal truncated tetrahedron. You can also see the 4 trigonal prisms sharing a face with the central tetrahedron, and nestled between the J26 cells.
Here are the coordinates I used (~ denotes vector concatenation; apacs/apecs are Wendy's usual abbreviations):
- Code: Select all
# x3o3o:
apecs<1/√2, 1/√2, 1/√2> ~ <-√(5/2)>
# o3x3o:
apacs<0, √2, √2> ~ <0>
# o3x3x:
apecs<1/√2, 1/√2, -3/√2> ~ <√(5/2)>
All in all, a very neatly-assembled CRF, with 1+4=5 tetrahedra, 4 trigonal prisms, 4 octahedra, 6 J26's, 4 trigonal cupolae, and 1 truncated tetrahedron, for a total of 24 cells.





