A different way to expand an ursatope?
102 posts
• Page 3 of 4 • 1, 2, 3, 4
Re: A different way to expand an ursatope?
... so far I do not see, how to cut off the remaining part of sidpixhi at the far end, while keeping it CRF. Sure, further diminishings are applicable, but no true deep cut. Thus it might be desirable to apply that 21-diminishing twice, i.e. once at each hemiglome. Providing then a 42-diminishing ...
Starting from sidpith then there we had 600 tets, 1200 trips, 720 pips, and 120 does. In that 42-diminishing we clearly cut off 42 does. In order to get a srid facet we ask not only to reduce by 1 doe, but also by 20 tets, by 30 trips, and by 12 pips. But then we have these tedrids, i.e. srids which intersect. This overlap each would overestimate the reduction by 1 pip, by 5 trips, and by 5 tets.
As each of those 2 tedrid layers consistss of 20 tedrids. Any tedrid introduces 3 decagons. But at each decagon there connect 2 tedrids. Thus, at each hemiglome we have 20*3/2 = 30 such overestimations.
Therefore the considered 42-diminishing of sidpith thus would have
600-2*20-2*20*20+2*30*5 = 60 tets,
1200-2*30-2*20*30+2*30*5 = 240 trips,
720-2*12-2*20*12+2*30*1 = 276 pips,
120-2*1-2*20*1+2*30*0 = 78 does,
0+2*1+2*20-2*20 = 2 srids,
0+0*1+0*20+2*20 = 40 tedrids
--- rk
Starting from sidpith then there we had 600 tets, 1200 trips, 720 pips, and 120 does. In that 42-diminishing we clearly cut off 42 does. In order to get a srid facet we ask not only to reduce by 1 doe, but also by 20 tets, by 30 trips, and by 12 pips. But then we have these tedrids, i.e. srids which intersect. This overlap each would overestimate the reduction by 1 pip, by 5 trips, and by 5 tets.
As each of those 2 tedrid layers consistss of 20 tedrids. Any tedrid introduces 3 decagons. But at each decagon there connect 2 tedrids. Thus, at each hemiglome we have 20*3/2 = 30 such overestimations.
Therefore the considered 42-diminishing of sidpith thus would have
600-2*20-2*20*20+2*30*5 = 60 tets,
1200-2*30-2*20*30+2*30*5 = 240 trips,
720-2*12-2*20*12+2*30*1 = 276 pips,
120-2*1-2*20*1+2*30*0 = 78 does,
0+2*1+2*20-2*20 = 2 srids,
0+0*1+0*20+2*20 = 40 tedrids
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
student91 wrote:So far I've got the following tower:.
- Code: Select all
x3o5x||x3o5f||x3f5o||F3x5o||V3x5o||F3f5o||(x3F5o+V3o5f)||f3x5f||o3x5F||(???)||(V+x)3o5x
I'm not sure what should be inserted into the (???), all other is just the tedrids and the completed dodecahedra.
Wrangled it out now, that mentioned 42-diminishing of sidpixhi - with 696 cells and 1560 vertices! - is given by
- Code: Select all
xxxFVF(xV)f(oB)F(oB)f(xV)FVFxxx-3-oofxxf(Fo)x(xo)x(xo)x(Fo)fxxfoo-5-xfoooo(of)f(Fx)x(Fx)f(of)oooofx-&#xt
i.e. could be given as the tower stack
- Code: Select all
x3o5x || x3o5f || x3f5o || F3x5o || V3x5o || F3f5o || (x3F5o + V3o5f) || f3x5f || (o3x5F + B3o5x) || F3x5x || ...
(where the rightmost given layer is the equatorial one, beyond the former ones reoccur in reversed order). Here B = V+x = F+f = 2f+x.
--- rk
Edit: sidpith ought have been sidpixhi, for sure.
Last edited by Klitzing on Fri Apr 08, 2016 7:06 am, edited 1 time in total.
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Klitzing wrote:[...]
Wrangled it out now, that mentioned 42-diminishing of sidpith - with 696 cells and 1560 vertices! - is given by
- Code: Select all
xxxFVF(xV)f(oB)F(oB)f(xV)FVFxxx-3-oofxxf(Fo)x(xo)x(xo)x(Fo)fxxfoo-5-xfoooo(of)f(Fx)x(Fx)f(of)oooofx-&#xt
i.e. could be given as the tower stack
- Code: Select all
x3o5x || x3o5f || x3f5o || F3x5o || V3x5o || F3f5o || (x3F5o + V3o5f) || f3x5f || (o3x5F + B3o5x) || F3x5x || ...
(where the rightmost given layer is the equatorial one, beyond the former ones reoccur in reversed order). Here B = V+x = F+f = 2f+x.
--- rk
Whoa. I definitely have to look into this one! Sounds utterly fascinating!
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
P.S. but surely you mean 42-diminishing of sidpixhi (x5o3o3x), not sidpith (x4o3o3x)?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
quickfur wrote:P.S. but surely you mean 42-diminishing of sidpixhi (x5o3o3x), not sidpith (x4o3o3x)?



 yep, for sure
yep, for sure--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
BTW, for the past few weeks I've been working on and off on completing Klitzing's idea of a trigonal J82 polychoron (attach 3 J82's around a triangular prism and fill in the rest). So far I've gotten up to the bottom of the J82's by filling in the gaps between them with mibdies, cuboctahedra, and truncated tetrahedra, but haven't found a way to close up the bottom of the polytope in a CRF way just yet. I'm getting bottom cells with edge length 2, that suggest incomplete hexagons, but there isn't enough space to actually complete the hexagons in a convex way. Any ideas?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
quickfur wrote:BTW, for the past few weeks I've been working on and off on completing Klitzing's idea of a trigonal J82 polychoron (attach 3 J82's around a triangular prism and fill in the rest). So far I've gotten up to the bottom of the J82's by filling in the gaps between them with mibdies, cuboctahedra, and truncated tetrahedra, but haven't found a way to close up the bottom of the polytope in a CRF way just yet. I'm getting bottom cells with edge length 2, that suggest incomplete hexagons, but there isn't enough space to actually complete the hexagons in a convex way. Any ideas?
Just to provide some links back and one minor correction: --- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Oops you're right, it's J81, not J82. 
OK, here's the lace tower(? - more like a split tower? Not sure) I have so far:
It's not really a lace city because the layout doesn't reflect the actual shape of the polytope, but the edges are intended just to show where the lacing edges are. The CD symbols appear in the order of their 4th coordinate from top to bottom.
The bottom of the J81's is at x2F3x. The other layers that don't lie on the main tower of the J81's were added in order to (try to) make CRF closure of the top layers; there are probably other ways of doing this than what I've done here. Starting from x2o3V and below, the CD symbols probably need to be replaced to make a CRF closure, but the ones I have so far show what I'm currently working with. The x2u3o seems to be a dead end, since I can't find any way of closing it in a CRF way (above it are several incomplete hexagons that, if completed, would produce self-intersections). But the 4D curvature here is quite shallow (almost perpendicular to the axis of the tower), so there's not much wiggling room for adding new cells. Unless we cut the tower all the way back to x2F3x and introduce a rounder "corona" (larger curvature and more vertex layers) in order to close up the shape, I'm not sure.

OK, here's the lace tower(? - more like a split tower? Not sure) I have so far:
- Code: Select all
# x2o3x
# |
# F2o3f
# / \
# A2x3o \
# | V2o3F
# | / \
# B2x3x F2o3A
# | | | \
# W2o3x | | \
# | D2f3x | \
# | /| \ | x2o3B
# | / | V2x3F |
# B2o3u | \ |
# | | f2x3V
# X2x3x | / |
# A2F3o / |
# \ / |
# F2u3f |
# /|\ |
# o2f3F | \ |
# x2F3x \ |
# | \x2o3V
# | \ |
# | u2x3f
# | |
# | F2x3o
# | /
# x2u3o
#
# A = f+2x
# B = f^3
# V = 2f
# W = 3f
# u = 2x
It's not really a lace city because the layout doesn't reflect the actual shape of the polytope, but the edges are intended just to show where the lacing edges are. The CD symbols appear in the order of their 4th coordinate from top to bottom.
The bottom of the J81's is at x2F3x. The other layers that don't lie on the main tower of the J81's were added in order to (try to) make CRF closure of the top layers; there are probably other ways of doing this than what I've done here. Starting from x2o3V and below, the CD symbols probably need to be replaced to make a CRF closure, but the ones I have so far show what I'm currently working with. The x2u3o seems to be a dead end, since I can't find any way of closing it in a CRF way (above it are several incomplete hexagons that, if completed, would produce self-intersections). But the 4D curvature here is quite shallow (almost perpendicular to the axis of the tower), so there's not much wiggling room for adding new cells. Unless we cut the tower all the way back to x2F3x and introduce a rounder "corona" (larger curvature and more vertex layers) in order to close up the shape, I'm not sure.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Considered that one again and did lots of calculations.
Esp. found: your "D" is nothing but "B" again and your "X" is again "A".
For the respective circumradii I got:
And for the heights between edgewise connected layer-vertices I got:
I even derived therefrom an ASCII art to scale stacking - with potential further continuations (layer 22 resp. 22'):
We both tried the general continuation with trips attached to the squares of mabidrid, with tricues (or coes) attached to the triangles, and teddies (or mibdies, gyepip, paps,...) attached to the pentagons. Atop the central trip we thus get in axial direction: |trip-(3)-teddi-(3)-co-(3)-tut-(6)-tricu-(3)->; in radial direction we have |trip-(4)-mabidrid-(4)-trip-(2)-> respectively |trip-(2)-{10}-(2)-mibdi-(2)->.
But you are right. The 2 triangles next to the opposite square of each mabidrid asks for some tricu shaped neighbour.
Therefore the only possibility is indeed to un-build at least down to vertex type 17, then somehow breaking with the above given general attachment rule. But then I fear that the so far already imposed restrictions just force the remaining mabidrid neighbours to be just as so far considered...
--- rk
Esp. found: your "D" is nothing but "B" again and your "X" is again "A".
For the respective circumradii I got:
- Code: Select all
1 = x2o3x - r=0,763762616 = sqrt(7/12)
2 = F2o3f - r=1,608167742 = sqrt((33+13*sqrt(5))/24)
3 = A2x3o - r=1,898914379 = sqrt((53+15*sqrt(5))/24)
4 = V2o3F - r=2,214211969 = sqrt((8+3*sqrt(5))/3)
5 = B2x3x - r=2,342235679 = sqrt((39+12*sqrt(5))/12)
6 = F2o3A - r=2,465140051 = sqrt((81+29*sqrt(5))/24)
7 = W2o3x - r=2,494776505 = sqrt((89+27*sqrt(5))/24)
8 = B2f3x - r=2,496282029 = sqrt((39+16*sqrt(5))/12)
9 = x2o3B - r=2,496282029 (same as 8)
10 = V2x3F - r=2,471587743 = sqrt((21+7*sqrt(5))/6)
11 = B2o3u - r=2,412343531 = sqrt((43+12*sqrt(5))/12)
12 = f2x3V - r=2,357380568 = sqrt((73+27*sqrt(5))/24)
13 = A2x3x - r=2,067012938 = sqrt((23+5*sqrt(5))/8)
14 = A2F3o - r=2,357380568 (same as 12)
15 = F2u3f - r=2,235671297 = sqrt((73+21*sqrt(5))/24)
16 = o2f3F - r=2,137615801 = sqrt((7+3*sqrt(5))/3)
17 = x2F3x - r=1,934092031 = sqrt((27+8*sqrt(5))/12)
18 = x2o3V - r=1,934092031 (same as 17)
19 = u2x3f - r=1,656911583 = sqrt((6+sqrt(5))/3)
20 = F2x3o - r=1,430684740 = sqrt((29+9*sqrt(5))/24)
21 = x2u3o - r=1,258305739 = sqrt(19/12)
And for the heights between edgewise connected layer-vertices I got:
- Code: Select all
1+2 - h=0,467086179 = sqrt((3+sqrt(5))/24) a = f*b
2+3 - h=0,288675135 = sqrt(1/12) b
2+4 - h=0,755761314 = sqrt((7+3*sqrt(5))/24) a+b
3+5 - h=0,755761314 a+b
4+5 - h=0,288675135 b
4+6 - h=0,755761314 a+b
5+7 - h=0,755761314 a+b
5+8 - h=0,934172359 = sqrt((3+sqrt(5))/6) a+a
6+9 - h=0,467086179 a
6+10 - h=0,755761314 a+b
7+8 - h=0,178411045 = sqrt((3-sqrt(5))/24) a-b
7+11 - h=0,755761314 a+b
8+10 - h=0,288675135 b
8+11 - h=0,577350269 = sqrt(1/3) b+b
8+14 - h=0,755761314 a+b
9+12 - h=0,755761314 a+b
10+11 - h=0,288675135 b
10+12 - h=0,467086179 a
10+15 - h=0,755761314 a+b
11+13 - h=0,755761314 a+b
12+15 - h=0,288675135 b
12+16 - h=0,467086179 a
12+18 - h=0,755761314 a+b
13+14 - h=0,577350269 b+b
13+15 - h=0,288675135 b
13+19 - h=0,467086179 a
14+15 - h=0,288675135 b
15+17 - h=0,467086179 a
15+19 - h=0,755761314 a+b
16+17 - h=0,288675135 b
16+18 - h=0,288675135 b
17+19 - h=0,288675135 b
17+21 - h=0,577350269 b+b
18+19 - h=0,288675135 b
19+21 - h=0,288675135 b
13+20 - h=0,645497224 = sqrt(5/12) 2a-b = a+a-b
20+21 - h=0,110264090 = sqrt((7-3*sqrt(5))/24) 2b-a = b+b-a
I even derived therefrom an ASCII art to scale stacking - with potential further continuations (layer 22 resp. 22'):
- Code: Select all
1 = x2o3x - r=0,763762616 ---
|
a
|
|
2 = F2o3f - r=1,608167742 ---
b
|
3 = A2x3o - r=1,898914379 ---
4 = V2o3F - r=2,214211969
5 = B2x3x - r=2,342235679
6 = F2o3A - r=2,465140051
7 = W2o3x - r=2,494776505
8 = B2f3x - r=2,496282029 + 9 = x2o3B
10 = V2x3F - r=2,471587743
11 = B2o3u - r=2,412343531
14 = A2F3o - r=2,357380568 + 12 = f2x3V
15 = F2u3f - r=2,235671297
16 = o2f3F - r=2,137615801
13 = A2x3x - r=2,067012938
18 = x2o3V - r=1,934092031 + 17 = x2F3x
19 = u2x3f - r=1,656911583
20 = F2x3o - r=1,430684740
21 = x2u3o - r=1,258305739 + 22' = x2(-v)3(V-x) : Ansatz 16+17+18+19+21+22'(+23) = co - but see below
22 = o2x3(-v) - r=0,504622639 = sqrt((3-sqrt(5))/3) : Ansatz 16+17+18+19+21 = tricu and 18+19+21+22 = tut - but see below
We both tried the general continuation with trips attached to the squares of mabidrid, with tricues (or coes) attached to the triangles, and teddies (or mibdies, gyepip, paps,...) attached to the pentagons. Atop the central trip we thus get in axial direction: |trip-(3)-teddi-(3)-co-(3)-tut-(6)-tricu-(3)->; in radial direction we have |trip-(4)-mabidrid-(4)-trip-(2)-> respectively |trip-(2)-{10}-(2)-mibdi-(2)->.
But you are right. The 2 triangles next to the opposite square of each mabidrid asks for some tricu shaped neighbour.
- When assumed to be a true tricues (incident vertices then are of type 16+17+18+19+21), the then introduced hexagons (tricu bases) give space for a tut (incident vertices then are of type 18+19+21+22). But then 22 calculates to be o2x3(-v) [where v=f-x=0,618], showing that these tuts would reach beyond the 21-21 edge, q.e. these 2 neighbouring ones would intersect.
- When assuming to be coes instead (incident vertices then are of type 16+17+18+19+21+22'+23), one derives for the type 22' vertices (23 not even was considered then) to be x2(-v)3(V-x) [where V=2f, thus V-x=2.236]. Again that (-v) shows that these coes would reach beyond the 18-18 edge, q.e. these 2 neighbouring ones would intersect.
Therefore the only possibility is indeed to un-build at least down to vertex type 17, then somehow breaking with the above given general attachment rule. But then I fear that the so far already imposed restrictions just force the remaining mabidrid neighbours to be just as so far considered...

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:Klitzing wrote:[...]
Thus, what then would be xfox-2-oxfo-P-oooo-&#xt (P=3,4,5)? - I will have to take a look into these...
--- rk
Good news!! While the case of P=4 doesn't seem to close up in a CRF way, I have just constructed the P=3 case (with a slight modification) and verified that it's CRF!!!!!! The slight adjustment is that the last vertex layer must be x2o3x, not x2o3o, otherwise the mibdies are non-corealmar. So the corrected symbol is xfox-2-oxfo-3-ooox&#xt (note the last x in place of o).
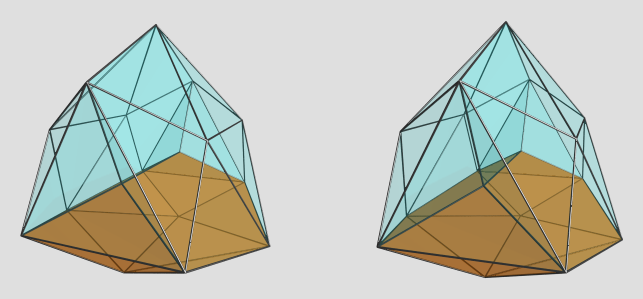
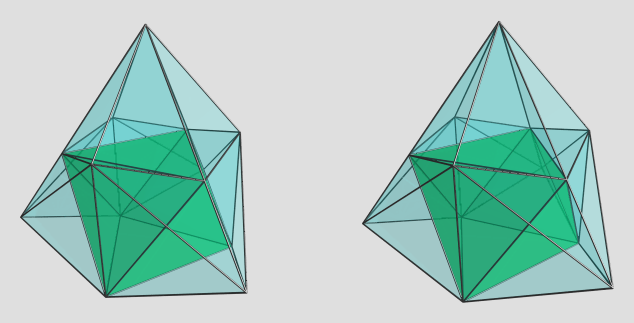
This is a truly beautiful little CRF; it has 3 mibdies and 2 tetrahedra on one side, 1 trigonal prism, 2 octahedra(!), 3 square pyramids, and 6 tetrahedra on the other side. Even better yet, it has 17 vertices and 17 cells -- the same number of vertices as cells!
Here's a look at the 3 mibdies surrounding an edge:
The 2 tetrahedra that fill in the gaps between the mibdies should be obvious.
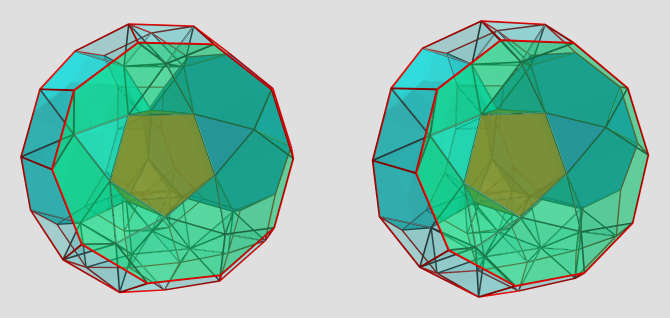
Now here's the far side, which has a most interesting configuration of cells:
I highlighted the trigonal prism which lies antipodal to the edge shared by the 3 mibdies. We see a most interesting pattern of tetrahedron-square pyramid-tetrahedron interfacing each mibdi to the trigonal prism.
Isn't it that the angles between the mibdi and any of the other cells are quite small here? Then one might consider to augment that fellow e.g. by 3 mibdi-pyramids.
As this former polychoron had a total cell count of 3 mibdies + 6+2 tets + 2 octs + 3 squippies + 1 trip the mere augmentation then ought have a total count of 6 peppies + 30+6+2 tets + 2 octs + 3 squippies + 1 trip.
I further considered the position of these 3 additional vertices. The former polychoron has been the tower x o3o || f x3o || o f3o || x o3x. Obviously the additional layer then has to be something of the form o o3#. The lacing conditions then brought up that # has to be x. Thus we'd get x o3o || o o3x || f x3o || o f3o || x o3x here.
But then it might be possible too that we don't have pentagon-wise connected pairs of peppies, but rather 5-fold rosettes of tets. Accordingly the total count well could be instead 15+30+6+2 tets + 2 octs + 3 squippies + 1 trip. (Depends on what would be the convex case.)
In the former case, by mere augmentations, it also becomes obvious, that we could have any number of augmentations, 1 to 3. In case when the rosettes would be needed, we just have the case with all 3 augmentations. Or it might occure that a single augmentation (using the peppies) would be convex, but 2 neighbouring ones would require an filled in rosette between neighbouring augmentations. Then also a bi-augmentation would become possible.
(Suppose quickfur could manage the needed convexity tests quite easy - and potentially even provide renderings of these up to 3 augmentation cases...)

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:Klitzing wrote:[...]
Got a promising idea! What then about teddi || ... || tedrid?
[...]
- Code: Select all
x3o f3o o3x teddi
o3x F3o f3x x3o
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f F3x V3x F3f Vx3oF f3x o3x tedrid
[...]
--- rk
Finally got around to this today. Very nice!!!! It has a beautiful arrangement of pentagonal rotundae connecting the teddi to the tetrid, and a fascinating cluster of octahedra around the bottom.
Here's a projection centered on the top teddi, with other teddies highlighted in yellow and midbies in magenta:
would it be possible to augment the tedrids of magnausaron with teddies?
Klitzing wrote:And here finally is its full Dynkin symbol:
- Code: Select all
xxFVF(Vx)fox-3-ofxxf(oF)xxx-3-xoooo(xo)xfo-&#xt
(Cf. esp. the layers which contained those unknown quantities B,C,D.)
--- rk
I just can't figure the lace city/tower out, sicne magnausaron doesn't have a proper lace city, and the augmentation only a lace city :/
- student5
- Dionian
- Posts: 48
- Joined: Tue Feb 18, 2014 2:48 pm
Re: A different way to expand an ursatope?
hi guys, I think ike||tetrid is a feasible option as well,
Consider as an augmentation of the earlier:
now consider id||ike, which has (according to my 4D insight :p ) a lot of octahedra, and pentagonal pyramids. now, diminish the ike to a pep and the id to a rotunda, and you get an augmentation of the rotunda with lots of octs and peps, which would have the same structure as the bottom part?
now the ike pyramid via diminishing and partial stott gives:
the only question is, if a point can be added to make pep||rotunda, but since ike||id is possible, I hope so
I think the coordinates are:
now, let's hope it's CRF :p
edit: fixed the mistake in the lace city pointed out by Klitzing
Consider as an augmentation of the earlier:
quickfur wrote:Klitzing wrote:[...]
Got a promising idea! What then about teddi || ... || tedrid?
[...]
- Code: Select all
x3o f3o o3x teddi
o3x F3o f3x x3o
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f F3x V3x F3f Vx3oF f3x o3x tedrid
[...]
--- rk
Finally got around to this today. Very nice!!!! It has a beautiful arrangement of pentagonal rotundae connecting the teddi to the tetrid, and a fascinating cluster of octahedra around the bottom.
[...]
Here are the pentagonal rotundae wrapping around the teddi:
Each pair of rotundae shares a triangular face.
now consider id||ike, which has (according to my 4D insight :p ) a lot of octahedra, and pentagonal pyramids. now, diminish the ike to a pep and the id to a rotunda, and you get an augmentation of the rotunda with lots of octs and peps, which would have the same structure as the bottom part?
now the ike pyramid via diminishing and partial stott gives:
- Code: Select all
o5o
o5o x5o o5x o5o
diminish:
o5o
o5o x5o o5x
o5o
o5o (-x)5f o5x
partial stott:
x5o
x5o o5f x5x
the only question is, if a point can be added to make pep||rotunda, but since ike||id is possible, I hope so

I think the coordinates are:
- Code: Select all
x3o o3f f3o o3x ike
o3x x3f F3o f3f o3F f3x x3o id
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f oF3Vx f3F V3x x3V F3f Vx3oF f3x o3x srid
diminish:
x3o o3f f3o o3x ike
o3x x3f F3o f3f o3F f3x x3o id
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f F3x V3x F3f Vx3oF f3x o3x srid
now, let's hope it's CRF :p
edit: fixed the mistake in the lace city pointed out by Klitzing
Last edited by student5 on Sat Jun 25, 2016 2:26 am, edited 1 time in total.
- student5
- Dionian
- Posts: 48
- Joined: Tue Feb 18, 2014 2:48 pm
Re: A different way to expand an ursatope?
on another thought... it looks to me like we are doing a caleidoscopic faceting, but now with mirrors intersecting the polytope!
consider the 2D example of taking a hexagon, and placing two mirrors at 60 degrees inside them. the resulting faceting would then be a rhombic tiling
so, take ike from edge-view

and, using the top middle triangle to rotate around, we get the (augmented) northern hemisphere of this interesting baby
now, in the case of the hexagon, the total angle ouside the mirrors is the same as the angle between the mirrors, so they join perfectly in the middle.
in the case of ike, however, they don't seem to be equal, and therefore are at an angle.
after second thought, the case pentagon-great dodecahedron works better:

you can see here that the mirrors are placed at the diagonals, and subsequently the polygons overlap. in the 4D equivalent this would be polyhedra, which is allowed
consider the 2D example of taking a hexagon, and placing two mirrors at 60 degrees inside them. the resulting faceting would then be a rhombic tiling

so, take ike from edge-view

and, using the top middle triangle to rotate around, we get the (augmented) northern hemisphere of this interesting baby
Klitzing wrote:quickfur wrote:[...]
Here's a look at the 3 mibdies surrounding an edge:
I further considered the position of these 3 additional vertices. The former polychoron has been the tower x o3o || f x3o || o f3o || x o3x. Obviously the additional layer then has to be something of the form o o3#. The lacing conditions then brought up that # has to be x. Thus we'd get x o3o || o o3x || f x3o || o f3o || x o3x here.
But then it might be possible too that we don't have pentagon-wise connected pairs of peppies, but rather 5-fold rosettes of tets. Accordingly the total count well could be instead 15+30+6+2 tets + 2 octs + 3 squippies + 1 trip. (Depends on what would be the convex case.)
--- rk
now, in the case of the hexagon, the total angle ouside the mirrors is the same as the angle between the mirrors, so they join perfectly in the middle.
in the case of ike, however, they don't seem to be equal, and therefore are at an angle.
after second thought, the case pentagon-great dodecahedron works better:

you can see here that the mirrors are placed at the diagonals, and subsequently the polygons overlap. in the 4D equivalent this would be polyhedra, which is allowed

- student5
- Dionian
- Posts: 48
- Joined: Tue Feb 18, 2014 2:48 pm
Re: A different way to expand an ursatope?
Hi student5,
welcome back. Yes, that teddy||...||tedrid - or "arsted biscrox" (the around-symmetrically tridiminished bistratic cap of the rectified hexacosachoron) - was designed as a diminishing of "biscrox" (the bistratic cap of the rectified hexacosachoron). The latter one clearly is nothing but the stack of 2 segmentochora: of ike||id and id||srid.
But it also is already known, that there is a similar segmentochoron id||tedrid = K4.136. Hence, I think you are after nothing else then the corresponding stack: ike||id||tedrid. - And, yes, that latter one truely is the former one, augmented at its 3 peroes by further known segmentochora: by peppy||pero = K4.139 (which likewise is a diminishing of ike||id). - Therefore your lace city looks a bit wrong. As both, the topmost ike and the medial id ought be complete. Just the bottom level should be diminished from srid to tedrid.
--- rk
welcome back. Yes, that teddy||...||tedrid - or "arsted biscrox" (the around-symmetrically tridiminished bistratic cap of the rectified hexacosachoron) - was designed as a diminishing of "biscrox" (the bistratic cap of the rectified hexacosachoron). The latter one clearly is nothing but the stack of 2 segmentochora: of ike||id and id||srid.
But it also is already known, that there is a similar segmentochoron id||tedrid = K4.136. Hence, I think you are after nothing else then the corresponding stack: ike||id||tedrid. - And, yes, that latter one truely is the former one, augmented at its 3 peroes by further known segmentochora: by peppy||pero = K4.139 (which likewise is a diminishing of ike||id). - Therefore your lace city looks a bit wrong. As both, the topmost ike and the medial id ought be complete. Just the bottom level should be diminished from srid to tedrid.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Klitzing wrote:quickfur wrote:Klitzing wrote:[...]
Thus, what then would be xfox-2-oxfo-P-oooo-&#xt (P=3,4,5)? - I will have to take a look into these...
--- rk
[...]
Here's a look at the 3 mibdies surrounding an edge:
The 2 tetrahedra that fill in the gaps between the mibdies should be obvious.
Now here's the far side, which has a most interesting configuration of cells:
I highlighted the trigonal prism which lies antipodal to the edge shared by the 3 mibdies. We see a most interesting pattern of tetrahedron-square pyramid-tetrahedron interfacing each mibdi to the trigonal prism.
Isn't it that the angles between the mibdi and any of the other cells are quite small here? Then one might consider to augment that fellow e.g. by 3 mibdi-pyramids.
[...]
(Suppose quickfur could manage the needed convexity tests quite easy - and potentially even provide renderings of these up to 3 augmentation cases...)
--- rk
Haha, well, computing the coordinates of the augments turned out to be quite hairy, since I didn't know beforehand the exact scaling of the Dynkin symbol for the 3 apices. That is, I know it must be of the form o2o3B for some B, but computing B involves solving 2 simultaneous quadratic equations in 2 variables, which in this case turned out to be particularly ugly. Fortunately, Wolfram Alpha came to the rescue and found two possible solutions, one of which is B=0 which is obviously not what we want, but the other is B=1, yielding o2o3x. Armed with that, computing the height is then relatively easy. And the convex hull algorithm proved that all edge lengths are equal.
So here is a look at this beauty:
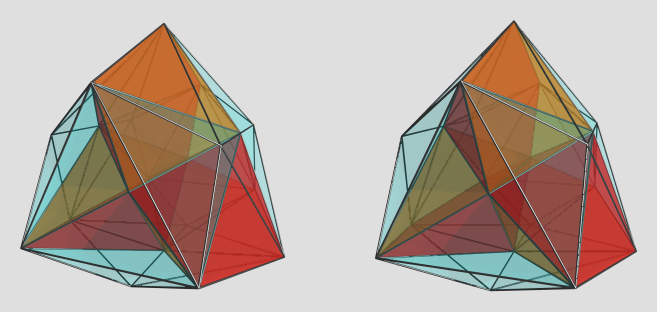
As I indicated to Klitzing via PM, the radius of the apices from the axis of the polytope is unlikely to be large, meaning the augments will be convex, so they retain the external cells of the augment, with only the J62 becoming internal as it attaches to the J62 cells of the original polytope. So each augment contributes 2 pentagonal pyramid cells. Shown above then are the 3 pairs of pentagonal pyramids, in alternating red/brown. The augments add quite a few tetrahedra, 10 each, so that brings the number of tetrahedra to 38. The original mibdies are gone, of course, and 6 pentagonal pyramids are added.
Six of these new tetrahedra, in 3 pairs, lie parallel to the axis of the polytope, i.e., lie on the equator:
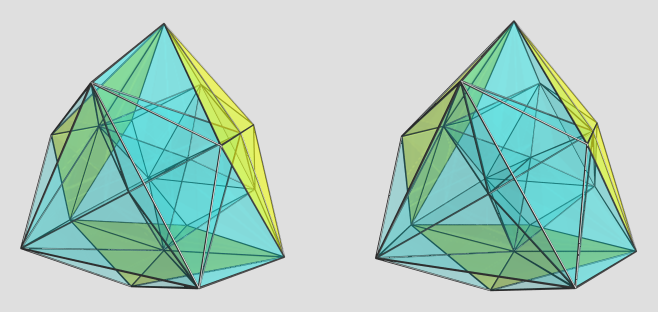
The far side of the polytope is unchanged.
Just for fun, here's a side view:
You can see some of the new tetrahedra here. The green cell is one of the octahedra that connects to the trigonal prism at the bottom. The pentagonal pyramids are actually also visible here, but harder to find because they have been foreshortened into planar scalene triangles. Their shared pentagonal faces project to the 3 long lines meeting at the top of the projection.
And of course, as per my policy of full disclosure, here are the coordinates of the triaugmented mibdi trigonal wedge (that's my tentative name for it
 ):
):- Code: Select all
# x2o3o
<±1, 0, 0, -phi^2/√3>
# f2x3o
<±phi, ±1, -1/√3, 0>
<±phi, 0, 2/√3, 0>
# o2f3o
<0, ±phi, -phi/√3, phi/√3>
<0, 0, 2*phi/√3, phi/√3>
# x2o3x
<±1, ±1, 1/√3, phi^2/√3>
<±1, 0, -2/√3, phi^2/√3>
# o2o3x (the 3 augments)
<0, ±1, 1/√3, (phi-2)/√3>
<0, 0, -2/√3, (phi-2)/√3>
where phi=(1+√5)/2 is the golden ratio.
Note that even though I listed o2o3x last, in terms of height it actually comes between x2o3o and f2x3o. So the lace tower is:
- Code: Select all
x2o3o
o2o3x
f2x3o
o2f3o
x2o3x
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Splendid pics, as usual!
That "B" shouldn't have been too hard - as I already provided to you its solution.
In fact I even provided your last stacking, as my subject line of that PM read:
x o3o || o o3x || f x3o || o f3o || x o3x.
--- rk
That "B" shouldn't have been too hard - as I already provided to you its solution.
In fact I even provided your last stacking, as my subject line of that PM read:
x o3o || o o3x || f x3o || o f3o || x o3x.

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Klitzing wrote:Splendid pics, as usual!
That "B" shouldn't have been too hard - as I already provided to you its solution.
In fact I even provided your last stacking, as my subject line of that PM read:
x o3o || o o3x || f x3o || o f3o || x o3x.
--- rk
I bury my head in shame. Clearly, I have been too long away from working with polytopes, and have forgotten the basics of working with them.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
To conclude, all 3 augmentations,
described as proposals already in http://hi.gher.space/forum/viewtopic.php?p=24760#p24760, do exist.
The total cell count then is (k=0,...,3):
Yeah!
--- rk
described as proposals already in http://hi.gher.space/forum/viewtopic.php?p=24760#p24760, do exist.
The total cell count then is (k=0,...,3):
- 3 - k mibdies (J62)
- 8 + 10*k tets
- 2 octs
- 3 squippies (J1)
- 1 trip
- 0 + 2*k peppies (J2)
Yeah!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
This makes me wonder, do augmented ursatopes exist too? Ostensibly, the tetrahedral teddy should be augmentable by a 5-cell on the top tetrahedron (analogous to the 3D augmented teddi, J64), or up to 3 teddi pyramids on one of the side cells. If these augmentations exist, perhaps augmentations of the expanded ursachora might exist too?
Higher-dimensional teddies might also be augmentable this way with an (n-1)-simplex, or teddy (pseudo)pyramids, if those exist? HIgher-dimensional teddy pyramids seem unlikely to be CRF, though, because they are generally non-orbiform.
The analogy of J64 also suggests that perhaps, a suitably diminished 600-cell might be convexly augmentable with a 5-cell on one of its tetrahedra? Not sure if this would be any different from an augmented tetrahedral teddy, though.
Higher-dimensional teddies might also be augmentable this way with an (n-1)-simplex, or teddy (pseudo)pyramids, if those exist? HIgher-dimensional teddy pyramids seem unlikely to be CRF, though, because they are generally non-orbiform.
The analogy of J64 also suggests that perhaps, a suitably diminished 600-cell might be convexly augmentable with a 5-cell on one of its tetrahedra? Not sure if this would be any different from an augmented tetrahedral teddy, though.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
I just calculated the dichoral angles of the bases of the ursachora, and it turns out all of them can be augmented: if my calculations are correct(EDIT:They're not, look at the bottom of this post), the tetrahedral one has a dichoral angle of exactly 72 degrees, thus adding a pen (dichoral angle of 75.5224) does not make the total exeed 180.quickfur wrote:This makes me wonder, do augmented ursatopes exist too? Ostensibly, the tetrahedral teddy should be augmentable by a 5-cell on the top tetrahedron (analogous to the 3D augmented teddi, J64), or up to 3 teddi pyramids on one of the side cells. If these augmentations exist, perhaps augmentations of the expanded ursachora might exist too?
The octahedral one has a dichoral angle of 112.4555 degrees, thus adding an octpy (dichoral angle of 60) does not make the total exeed 180 either.
The icosahedral one can easilly be seen to be augmentable by looking at ex.
Now for the next question: can the teddi's themself be augmented? I'd say yes, because it can be done in ex, and the dichoral angles get only sharper (i.e. more space to put things), thus adding extra teddi-pyramids shouldn't pose a problem. However,, in ex there are some gaps that can be filled up with peppypys, which can't be done when the angles do not mach up. However, at least one augmentation should be possible I guess.
Then on to the generalization: The tetrahedral ursachoron augmentation looks like o3o3o||x3o3o||(f3o3o||o3x3o), then an expansion makes the teddi's into tridiminished rhombicosidodecahedra, and the x3o3o gets turned into a x3o3x, thus logically the o3o3o should turn into a o3o3x. The only new angles, that thus need to be checked, are the one at the .3o3x and the x3.3x of the x3o3x. If this one is less than 180, the result thus is convex.
Thus it seems the augmented tridiminished icosahedron doesn't have any simple generalizations into 4d.
The generalization of the laminar augmentation is not entirely clear, mostly because a lot changes in the "expansion" from ursachoron to magnaursachoron, thus actually this just gives a related but not similar problem.
EDIT: Whoops, calculated the wrong angle, I calculated the one between two teddi's, the actual angle at a triangle of the tetrahedral ursachoron is arccos(1/(sqrt(10)-3sqrt(2))), approximately 97.7 degrees. So an expansion at the tip is still possible for the tetrahedral ursachoron.
The octahedral one has an angle of arccos(-sqrt(7/4-3sqrt(5)/4)), approximately 105.7<180-60, so that one is also possible. The icosahedral one can be seen to be possible by looking at ex.
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: A different way to expand an ursatope?
@student91: are you sure your calculations are correct? 'cos I just built a model of the tetraaugmented tetrahedral teddy, and AFAICT, it's CRF!!! 




The lace tower is:
The apices of the augments are, obviously, o3o3x. And obviously, there are lacing edges from x3o3o to f3o3o. Each augment introduces 3 pentagonal pyramid cells, so there are 12 pentagonal pyramids in 6 pairs. The octahedron and 4 tetrahedra at the bottom are unchanged.
I'm still trying to find a good 4D viewpoint for rendering it, so pics will have to wait. But this is so awesome I just wanted to get it off my chest first.
Edit: here's a render of this beautiful CRF polychoron:

I'm running out of time, so can't do a more selective coloring of cells just yet, but this should at least show enough of the structure for it to be understood. The green part at the bottom is the octahedron at the bottom of the teddy. The 4 red tetrahedra are the 4 original tetrahedra in the unaugmented teddy. (Well, only one of them is completely seen, actually, the rest are on the far side of the polytope so only some of their faces are seen here. I didn't want to turn off clipping because that would obscure the pentagonal pyramids.) There are 4 new tetrahedra that are now connected to the octahedron where there used to be 4 teddies; these are connected to the exposed green faces in the above image. Both types of tetrahedra share an edge with the pentagonal pyramid cells. If you look carefully you can see 3 of the 6 pairs of pentagonal pyramids here, looping around the central axis of the projection. Each pair shares a triangular face with an adjacent pair. (Sorry, have to find some other time to do a rendering to highlight this.)
One thing very interesting about this CRF: it's almost what I call a "pyramidotope": a generalization of a deltatope by relaxing the restriction of facets to be (n-1)-simplexes to allow other kinds of pyramids as well. The only non-pyramid cell here is the octahedron. Unfortunately I don't think the octahedron is augmentable because of the shallow dichoral angle with the tetrahedra, otherwise it could become a true pyramidotope. But in any case, the rest of this CRF is made of tetrahedra and pentagonal pyramids. If we generalize our definition of corona to allow any kind of pyramids other than (n-1)-simplexes, then this CRF could be construed to be a kind of "octahedron corona", a kind of 4D analogue of things like, say, sphenocorona or sphenomegacorona.
Here's the coordinates:





The lace tower is:
- Code: Select all
x3o3o
o3o3x
f3o3o
o3x3o
The apices of the augments are, obviously, o3o3x. And obviously, there are lacing edges from x3o3o to f3o3o. Each augment introduces 3 pentagonal pyramid cells, so there are 12 pentagonal pyramids in 6 pairs. The octahedron and 4 tetrahedra at the bottom are unchanged.
I'm still trying to find a good 4D viewpoint for rendering it, so pics will have to wait. But this is so awesome I just wanted to get it off my chest first.

Edit: here's a render of this beautiful CRF polychoron:

I'm running out of time, so can't do a more selective coloring of cells just yet, but this should at least show enough of the structure for it to be understood. The green part at the bottom is the octahedron at the bottom of the teddy. The 4 red tetrahedra are the 4 original tetrahedra in the unaugmented teddy. (Well, only one of them is completely seen, actually, the rest are on the far side of the polytope so only some of their faces are seen here. I didn't want to turn off clipping because that would obscure the pentagonal pyramids.) There are 4 new tetrahedra that are now connected to the octahedron where there used to be 4 teddies; these are connected to the exposed green faces in the above image. Both types of tetrahedra share an edge with the pentagonal pyramid cells. If you look carefully you can see 3 of the 6 pairs of pentagonal pyramids here, looping around the central axis of the projection. Each pair shares a triangular face with an adjacent pair. (Sorry, have to find some other time to do a rendering to highlight this.)
One thing very interesting about this CRF: it's almost what I call a "pyramidotope": a generalization of a deltatope by relaxing the restriction of facets to be (n-1)-simplexes to allow other kinds of pyramids as well. The only non-pyramid cell here is the octahedron. Unfortunately I don't think the octahedron is augmentable because of the shallow dichoral angle with the tetrahedra, otherwise it could become a true pyramidotope. But in any case, the rest of this CRF is made of tetrahedra and pentagonal pyramids. If we generalize our definition of corona to allow any kind of pyramids other than (n-1)-simplexes, then this CRF could be construed to be a kind of "octahedron corona", a kind of 4D analogue of things like, say, sphenocorona or sphenomegacorona.
Here's the coordinates:
- Code: Select all
# x3o3o
apecs<1/√2, 1/√2, 1/√2> ~ <phi^2/√2>
# f3o3o
apecs<phi/√2, phi/√2, phi/√2> ~ <0>
# o3x3o
apacs<√2, 0, 0> ~ <-phi/√2>
# o3o3x: teddi pyramid apices
apecs<1/√2, 1/√2, -1/√2> ~ <1/(phi*√2)>
Last edited by quickfur on Sat Jul 02, 2016 4:33 am, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Also, it is possible to augment the tetrahedral teddy with a 5-cell on the top tetrahedron. However, this augment cannot coexist with the teddi pyramid augments, because it would cause a concave curve between the 5-cell augment and the teddi pyramid augments. The dichoral angle between the 5-cell augment and the adjacent teddi is 173.28 deg, which very close to corealmar, so there is no room left to fit a teddi augment and maintain convexity.
EDIT: Here is the 5-cell augmented tetrahedral teddy:
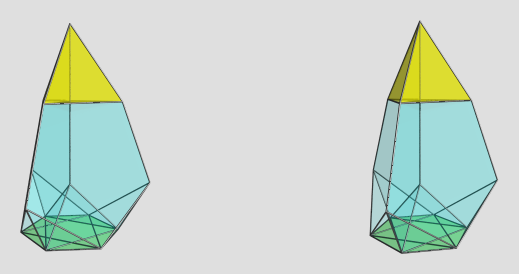
Its projection is very similar to the augmented tridiminished icosahedron in 3D.
Coordinates:
where phi=(1+√5)/2 is the golden ratio, and ~ denotes vector concatenation. (It's mainly just a convenient notation to allow using Wendy's apecs/apacs operators on an initial segment of a vector. Of course, my vector calculator program actually understands this notation, and generates the numerical values correctly.)
EDIT: Here is the 5-cell augmented tetrahedral teddy:

Its projection is very similar to the augmented tridiminished icosahedron in 3D.
Coordinates:
- Code: Select all
# x3o3o
apecs<1/√2, 1/√2, 1/√2> ~ <phi^2/√2>
# f3o3o
apecs<phi/√2, phi/√2, phi/√2> ~ <0>
# o3x3o
apacs<√2, 0, 0> ~ <-phi/√2>
# o3o3o: 5-cell on top of the top cell
<0, 0, 0, phi^2/√2 + (√10)/2>
where phi=(1+√5)/2 is the golden ratio, and ~ denotes vector concatenation. (It's mainly just a convenient notation to allow using Wendy's apecs/apacs operators on an initial segment of a vector. Of course, my vector calculator program actually understands this notation, and generates the numerical values correctly.)
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
I think I've found a proof that augmented teddies ought to exist in all dimensions, at least for the (n-1)-simplex teddies.
Consider a uniform truncated n-simplex (i.e., x3x3o3o...3o). We can augment it with n-simplexes, and obtain a larger n-simplex. Now suppose we only augment one of the truncated ends. Because of the correspondence with the n-simplex, the facets of the augment will be co(hyper)planar with the "side" cells of the truncated n-simplex, so it would blend to produce a cell in the shape of a similarly monoaugmented (n-1)-truncated simplex. Generally, this cell is non-CRF. But compare the truncated n-simplex with the n-simplex teddies. We can imagine a deformation process where the bottom facet of the truncated n-simplex is contracted from a truncated (n-1)-simplex to a rectified (n-1)-simplex (o3x3o3o...3o). This process pulls the side cells inward so that their difacetal angle with the top (n-1)-simplex cell is smaller. In the case of the teddy, these side cells themselves undergo an analogous contraction, but the overall effect is the reduction of the difacetal angle between the top cell and the side cells. Thus, by construction, the augment in the monoaugmented truncated (n-1)-simplex must now be no longer coplanar with the side cells; so where it attaches to what is now the (n-1)-simplex teddy will always be convex: the difacetal angle will always be <180 deg. Therefore it is always possible to augment an (n-1)-simplex teddy with an (n-1)-simplex on its top cell to produce a CRF n-dimensional analogue of the augmented tridiminished icosahedron.
I'm not sure if a similar proof is applicable for the lateral augments, though. One trouble is that starting from 4D, the n-simplex teddies are no longer orbiform, so we cannot simply generalize the augmentation to a teddy pyramid, as the latter won't be CRF anymore. Perhaps there can be some other kind of teddy pseudo-pyramid that might work as an augment, I'm not sure.
Anyway, when I get some free time again, I'll see if I can construct the augmentations of the octahedral/icosahedral teddies. Well, the icosahedral teddy is for sure augmentable, because it's just diminishing of the 600-cell. That seems to suggest that the octahedral teddy ought to be augmentable too. We'll see!
Consider a uniform truncated n-simplex (i.e., x3x3o3o...3o). We can augment it with n-simplexes, and obtain a larger n-simplex. Now suppose we only augment one of the truncated ends. Because of the correspondence with the n-simplex, the facets of the augment will be co(hyper)planar with the "side" cells of the truncated n-simplex, so it would blend to produce a cell in the shape of a similarly monoaugmented (n-1)-truncated simplex. Generally, this cell is non-CRF. But compare the truncated n-simplex with the n-simplex teddies. We can imagine a deformation process where the bottom facet of the truncated n-simplex is contracted from a truncated (n-1)-simplex to a rectified (n-1)-simplex (o3x3o3o...3o). This process pulls the side cells inward so that their difacetal angle with the top (n-1)-simplex cell is smaller. In the case of the teddy, these side cells themselves undergo an analogous contraction, but the overall effect is the reduction of the difacetal angle between the top cell and the side cells. Thus, by construction, the augment in the monoaugmented truncated (n-1)-simplex must now be no longer coplanar with the side cells; so where it attaches to what is now the (n-1)-simplex teddy will always be convex: the difacetal angle will always be <180 deg. Therefore it is always possible to augment an (n-1)-simplex teddy with an (n-1)-simplex on its top cell to produce a CRF n-dimensional analogue of the augmented tridiminished icosahedron.
I'm not sure if a similar proof is applicable for the lateral augments, though. One trouble is that starting from 4D, the n-simplex teddies are no longer orbiform, so we cannot simply generalize the augmentation to a teddy pyramid, as the latter won't be CRF anymore. Perhaps there can be some other kind of teddy pseudo-pyramid that might work as an augment, I'm not sure.
Anyway, when I get some free time again, I'll see if I can construct the augmentations of the octahedral/icosahedral teddies. Well, the icosahedral teddy is for sure augmentable, because it's just diminishing of the 600-cell. That seems to suggest that the octahedral teddy ought to be augmentable too. We'll see!

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Sneaked in some time for 4D geometry tonight...  Discovered that the octahedral teddy is not simultaneously augmentable by 8 teddi pyramids, because augmenting adjacent teddies produces a concave gap between the augments. It seems that for the icosahedral teddy, augmenting with teddi pyramids is also non-convex; however it just so happens to produce concave gaps which can be filled in by CRF pentagonal pyramid pyramids, which fill up the gap leaving only florets of tetrahedra on the surface. So the result is a convex fragment of the 600-cell's surface.
Discovered that the octahedral teddy is not simultaneously augmentable by 8 teddi pyramids, because augmenting adjacent teddies produces a concave gap between the augments. It seems that for the icosahedral teddy, augmenting with teddi pyramids is also non-convex; however it just so happens to produce concave gaps which can be filled in by CRF pentagonal pyramid pyramids, which fill up the gap leaving only florets of tetrahedra on the surface. So the result is a convex fragment of the 600-cell's surface.
However, non-adjacent augmentation does seem to be possible on the octahedral teddy. The maximum augmentation is 4 augments in tetrahedral symmetry (i.e., augment positions corresponding with all non-adjacent faces of the octahedron). I have not confirmed CRF-ness algebraically, because the algebra involved is too ugly and I'm too tired to figure it out right now. However, I derived the coordinates up to 15 decimal places, which, even though it's not proof, is at least a strong indication that the polychoron is CRF. Here's the lace tower:
However, I derived the coordinates up to 15 decimal places, which, even though it's not proof, is at least a strong indication that the polychoron is CRF. Here's the lace tower:
where A = approx 1.05066753090906. As I said, I don't know the algebraic representation of this number yet. Maybe some other time when I work through the algebra. I got this by manual application of Newton's method on a set of layer height / edge length constraints.
I got this by manual application of Newton's method on a set of layer height / edge length constraints.
Here's a quick render:
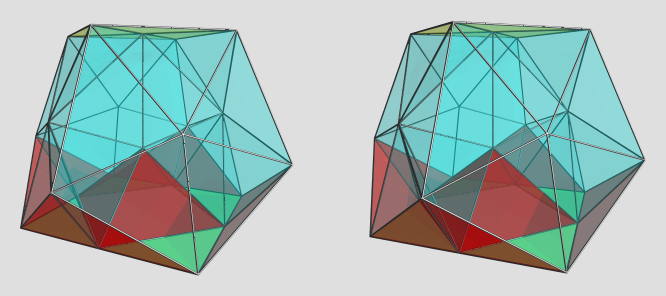
Two of the 4 augments are visible here on the left and right of the image. The front and back teddies are not augmented.
 Discovered that the octahedral teddy is not simultaneously augmentable by 8 teddi pyramids, because augmenting adjacent teddies produces a concave gap between the augments. It seems that for the icosahedral teddy, augmenting with teddi pyramids is also non-convex; however it just so happens to produce concave gaps which can be filled in by CRF pentagonal pyramid pyramids, which fill up the gap leaving only florets of tetrahedra on the surface. So the result is a convex fragment of the 600-cell's surface.
Discovered that the octahedral teddy is not simultaneously augmentable by 8 teddi pyramids, because augmenting adjacent teddies produces a concave gap between the augments. It seems that for the icosahedral teddy, augmenting with teddi pyramids is also non-convex; however it just so happens to produce concave gaps which can be filled in by CRF pentagonal pyramid pyramids, which fill up the gap leaving only florets of tetrahedra on the surface. So the result is a convex fragment of the 600-cell's surface.However, non-adjacent augmentation does seem to be possible on the octahedral teddy. The maximum augmentation is 4 augments in tetrahedral symmetry (i.e., augment positions corresponding with all non-adjacent faces of the octahedron). I have not confirmed CRF-ness algebraically, because the algebra involved is too ugly and I'm too tired to figure it out right now.
 However, I derived the coordinates up to 15 decimal places, which, even though it's not proof, is at least a strong indication that the polychoron is CRF. Here's the lace tower:
However, I derived the coordinates up to 15 decimal places, which, even though it's not proof, is at least a strong indication that the polychoron is CRF. Here's the lace tower:- Code: Select all
o4o3x
A4o3o
o4o3f
o4x3o
where A = approx 1.05066753090906. As I said, I don't know the algebraic representation of this number yet. Maybe some other time when I work through the algebra.
 I got this by manual application of Newton's method on a set of layer height / edge length constraints.
I got this by manual application of Newton's method on a set of layer height / edge length constraints.Here's a quick render:

Two of the 4 augments are visible here on the left and right of the image. The front and back teddies are not augmented.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Oh, and the octahedral teddy can be augmented with an octahedral pyramid; the latter being shallower than the 5-cell, apparently shallower enough to compensate for the increased dichoral angle between the top and side cells compared to the tetrahedral teddy, so that it remains convex. Here's a render:
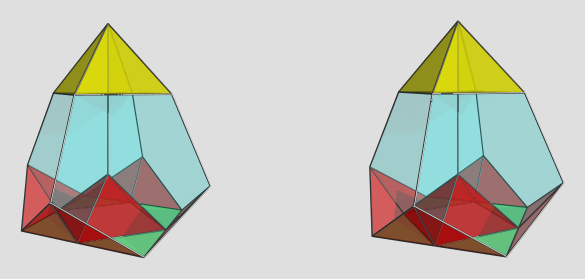
Coordinates:
However, this augment cannot exist simultaneously with the teddi augments and remain CRF, because they will create concave areas on the surface (the dichoral angle between the tetrahedra in the octahedral pyramid and the tetrahedra in the teddi pyramid is > 180 deg). So the octahedral teddy can be augmented either with an octahedral pyramid, or with up to 4 teddi pyramids, but not both, if we want the result to be CRF.

Coordinates:
- Code: Select all
# o4o3o: top augment with octahedral pyramid
<0, 0, 0> ~ <√(2*phi) + √2>
# o4o3x
apacs<0, 0, √2> ~ <√(2*phi)>
# o4o3f
apacs<0, 0, √2*phi> ~ <0>
# o4x3o
apacs<0, √2, √2> ~ <-√(2/phi)>
However, this augment cannot exist simultaneously with the teddi augments and remain CRF, because they will create concave areas on the surface (the dichoral angle between the tetrahedra in the octahedral pyramid and the tetrahedra in the teddi pyramid is > 180 deg). So the octahedral teddy can be augmented either with an octahedral pyramid, or with up to 4 teddi pyramids, but not both, if we want the result to be CRF.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
quickfur wrote:@student91: are you sure your calculations are correct? 'cos I just built a model of the tetraaugmented tetrahedral teddy, and AFAICT, it's CRF!!!



The lace tower is:
- Code: Select all
x3o3o
o3o3x
f3o3o
o3x3o
The apices of the augments are, obviously, o3o3x. And obviously, there are lacing edges from x3o3o to f3o3o. Each augment introduces 3 pentagonal pyramid cells, so there are 12 pentagonal pyramids in 6 pairs. The octahedron and 4 tetrahedra at the bottom are unchanged.
Sorry quickfur, but it seems that you considered the tetra-excavated tetrahedral teddi!
Cause the "mere" (i.e. un-augmented / un-excavated) tetrahedral teddi looks in appropriate lace city like this:
- Code: Select all
o o x x o o
f o o f
x o o x
Accordingly the augmentation ought be some #3o3o (or rather: o # # o), with "#" most probably even larger than f!
On the other hand, your proclaimed "tips" provide a dual tet of the same size and situated parallel to the bottom tet. Therefore the convex hull of just these 2 is nothing but the hex. So this, after all, provides a further interesting interrelation to the "mere" tetrahedral teddi!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:... Anyway, when I get some free time again, I'll see if I can construct the augmentations of the octahedral/icosahedral teddies. Well, the icosahedral teddy is for sure augmentable, because it's just diminishing of the 600-cell. That seems to suggest that the octahedral teddy ought to be augmentable too. We'll see!
quickfur wrote:Oh, and the octahedral teddy can be augmented with an octahedral pyramid ...
Well, we have the tetrahedral, the octahedral, and the icosahedral ursachoron (xfo3ooxPooo&#xt, P=3,4,5); but we have also their Stott expansions xfo3ooxPxxx&#xt, where obviously P can even be 2 as well.
You now have proved that we always can (mono-)augment at the first layer each for the first set, yielding: oxfo3oooxPoooo&#xt. - Then the corresponding mono-augmentation of the second set also should be possible: oxfo3oooxPxxxx&#xt. (The case P=2 there is immediate, as it is nothing but the prism of auteddi.)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Klitzing wrote:quickfur wrote:@student91: are you sure your calculations are correct? 'cos I just built a model of the tetraaugmented tetrahedral teddy, and AFAICT, it's CRF!!!



The lace tower is:
- Code: Select all
x3o3o
o3o3x
f3o3o
o3x3o
The apices of the augments are, obviously, o3o3x. And obviously, there are lacing edges from x3o3o to f3o3o. Each augment introduces 3 pentagonal pyramid cells, so there are 12 pentagonal pyramids in 6 pairs. The octahedron and 4 tetrahedra at the bottom are unchanged.
Sorry quickfur, but it seems that you considered the tetra-excavated tetrahedral teddi!
Cause the "mere" (i.e. un-augmented / un-excavated) tetrahedral teddi looks in appropriate lace city like this:
- Code: Select all
o o x x o o
f o o f
x o o x
Accordingly the augmentation ought be some #3o3o (or rather: o # # o), with "#" most probably even larger than f!
On the other hand, your proclaimed "tips" provide a dual tet of the same size and situated parallel to the bottom tet. Therefore the convex hull of just these 2 is nothing but the hex. So this, after all, provides a further interesting interrelation to the "mere" tetrahedral teddi!
--- rk
Are you sure about this? The height of the teddi pyramid is quite shallow, and note that o3o3x, being in dual configuration, protrudes from x3o3o quite a bit. Conceivably, due to the small dichoral angle between x3o3o and the teddi, the apex of the pyramids would actually fall on o3o3x. In fact I found o3o3x by solving for apex coordinates that are equidistant from each of the 3 cell layers, and yield unit edge lengths. Wouldn't this be the same thing as erecting CRF pyramids on the teddies?
In any case, if o3o3x is wrong, then what should be the correct symbol?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
In fact I found o3o3x by solving for apex coordinates that are equidistant from each of the 3 cell layers, and yield unit edge lengths. Wouldn't this be the same thing as erecting CRF pyramids on the teddies?
It does, but these pyramids either could dimple in or protrude out. (The tips then are mirror images wrt. the to be adjoined teddies.) Either way the "tip" coords would follow your constraint. But at most one of these 2 directions would result in a convex figure.
The total figure clearly is something of the form x3o3o || o3o3# || f3o3o || o3x3o.
I myself did not get that "#" so far, still working on it.
But at least found out that the un-augmented figure x3o3o || f3o3o || o3x3o is circumscribable (with circumradius 1 (in edge units))!
Its coords then are, when centered at the origin:
- (1/sqrt(2), 0, 0; 1/sqrt(2)) & all permutations in first 3 coord.s & all changes of sign in first 3 coord.s
- (f/sqrt(8), f/sqrt(8), f/sqrt(8); 1/(F sqrt(8))) & all even permutations in first 3 coord.s & all changes of sign in first 3 coord.s
- (1/sqrt(8), 1/sqrt(8), 1/sqrt(8); -sqrt(5/8)) & all even permutations in first 3 coord.s & all changes of sign in first 3 coord.s
The latter comes not out as too much an surprise, as that tetrahedral ursachoron happens to be the vertex figure of sadit = o3o3o4s3s = s3s3s4o3o = o4s3s3s4o = s3s3s *b3s4o = s3s3s *b3s *b3s (sadit = snub icositetrachoric tetracomb ).
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Well, then clearly # must be x, because if there is only one convex solution, it must be the one I found, as the polytope viewer would not produce the correct cells if I had found the other solution! 

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
102 posts
• Page 3 of 4 • 1, 2, 3, 4
Who is online
Users browsing this forum: No registered users and 47 guests