I'd like to hear any ideas about what it would be like to be a 4D being viewing 4D surroundings, and other 4D beings.
What would they likely be able to see and perceive?
4D Tetronion Viewing 4D Surroundings
13 posts
• Page 1 of 1
Re: 4D Tetronion Viewing 4D Surroundings
We've talked about this a lot, before.  You can look into the Higher Spatial Dimensions section of this forum to find many discussions along these lines.
You can look into the Higher Spatial Dimensions section of this forum to find many discussions along these lines.
Some of my early musings on this subject led me to the following scenarios. For ease of description, I'm going to describe just a single viewpoint, looking from the eyes of a Tetronian at some specific object in the scene. I'll describe the 4D objects in terms of the shapes of their 3D projections onto the Tetronian's retina.
I. Indoor scene
Looking from the eyes of a Tetronian sitting at his desk in his study, here's what he sees. The wall opposite him appears as a cube at the center of his field of vision. Four of the remaining 5 walls appear as frustums emanating from this cube; the 5th wall is behind him and thus unseen. There's a painting hung on this far wall, which appears as a cuboid somewhere on the upperleft back region of the wall's cubic surface; there's some random 3D objects depicted inside the cuboid of this picture. Below the cube of the far wall is another frustum, the image of the floor. A large part of this frustum is obscured by another brown frustum: the far end of his desk. On the desk is a writing pad, which appears as a white frustum inside the brown frustum, with some 3D curves drawn on it.
Now, on the left and front frustums (two of the 4 side walls connected to the far wall), there are frustum-shaped cutouts: the images of the two windows of the room. There's a crudely-conical shape in the cutout of the front frustum, which is truncated by the faces of the frustum: this is the image of the partially obscured mountain visible through this window. There's a horizontal plane dividing the left window's frustum into two halves; the top half is bluish -- the image of the sky outside -- and the bottom half is green -- the image of a flat grass field outside.
In the right frustum (the 4th side wall) there's a tall frustum cutout that reaches to the floor: this is the image of the doorway exiting the room. The door itself is currently not visible, because it opens outwards into the corridor beyond, and it's currently fully open. In the doorway's frustum image, a cuboid-shaped wall is visible: this is the far wall of the corridor that's partially visible from the desk. The remaining volume of the doorway's frustum is filled by triangular prisms: the one on top of the cuboid image of the wall is the partially-obscured image of the corridor's ceiling; the one below the cuboid is the partially-obscured image of the floor of the corridor. The two remaining ones in front and behind the cuboid are the partially-obscured images of two other corridor walls that are visible from the desk (this last part is a uniquely 4D phenomenon: in 3D, we can only ever see one corridor wall from this viewpoint).
Now, above the frustum-shaped image of the desk, somewhere off to the side, is a hemisphere: this is the image of a 4D ball lying on the floor behind the desk; it's partly obscured by the desk.
The Tetronian's arms are resting on the desk; they appear as truncated cones (or cylinders with unequal top/bottom radii, if you wish) emanating from the bottom of the projection volume, and extending diagonally about halfway to the top face of the frustum image of the desk.
II. Outdoor scene
All that description of indoor objects is getting a bit boring -- there are too many tesseractic shapes (which show up as cubes, frustums, and prisms in the projection image), which get a bit too "boxy" after a while. So now the Tetronian decides to get some fresh air outside. He walks out of the house, in the direction of the mountain described earlier, and looks outward in that direction.
Since the house is behind him, it is currently not visible. Instead, he's looking at the distant mountain, which appears as a roughly conical shape filling the center of his field of vision. There are many smaller cones arranged around the base of this big cone: these are the lower peaks and hills in front of the mountain. Some of them are incomplete cones that appear to have been "eaten out" by other cones that overlap their volumes. These are hills that lie behind, and are therefore partly obscured, by other hills in front of them.
From the bottom of the projection volume, there's a wide cone that covers most of the bottom area, but quickly tapers to a point above, somewhat spiralling as it goes. This is the image of the trail that leads to the mountain. Partway up this spiralling cone is a flattened tube shape that branches off and extends to the front of the projection volume. This is a side-trail that branches off the main one, leading somewhere else. Another branch occurs a little farther up the main trail, leading off to the left of the projection volume. This is a second side-trail that leads in another direction. Below these branches, there's a curious torus-shaped trail that encircle the main trail, but not connected to it. This is a crude jogging track not far from the Tetronian's house, that people use for exercise every now and then. Thanks to the extra dimension available, there's no need to put it off to the side of the main trail; it's more convenient to build it around the trail for easier accessibility. It's not connected to the main trail but can be reached by walking across the grassy area the lies between them.
Now, the entire projection volume has two halves, divided by a horizontal plane. This is the (literal!) horizon of the landscape. It is interrupted by the images of the mountain and hills in the middle (they lie closer to than the horizon and therefore obscure it). The upper half is bluish -- the image of the sky; and the lower half is green toward the bottom, but become brownish near the horizon -- the image of the ground, which is grassy near the Tetronian's house, but gradually become more rocky as you approach the mountain and hills. There's a small, partial sphere that sits on the images of the mountain and hills like a half-buried glowing crystal ball: this is the image of the setting sun, which is beginning to descend toward the horizon, partially behind the mountain. On the opposite side of the mountain's image, there's a dark region in the ground that extends away from the globe: this is the 3D shadow of the mountain cast by the sun behind it upon the ground.
In the upper half of the projection image are some amorphous greyish blobs -- these are the images of 4D clouds. If one looks carefully, one will notice that some blobs have been "carved out" by other blobs, some bigger, some smaller -- the "carved" blobs are clouds that are farther away in the 4th direction than the clouds corresponding to the blobs that carve it.
Around the fringes of the horizon, there's a band of vertical cylinders that are tall at the edges of the projection volume, but shrink to a short height as you move toward the center; they are capped by amorphous green blobs on top. These are trees in a forest that gird the mountain and hills. The taller part are trees near where the Tetronian is standing; the shorter part are trees farther away (and closer to the mountain). It is tempting to say that the forest surrounds the mountain, but that's not strictly true because it only goes around the mountain in a roughly toroidal region around the base of the mountainous area; the closest 3D analogue would be *two* forests on either side of a mountain -- but in 4D, it's possible for a single forest to extend around the sides of the mountain while still leaving an unforested swath of land in front of it.
III. Looking at the house
Argh, this is taking way to long to write down... maybe later.
 You can look into the Higher Spatial Dimensions section of this forum to find many discussions along these lines.
You can look into the Higher Spatial Dimensions section of this forum to find many discussions along these lines.Some of my early musings on this subject led me to the following scenarios. For ease of description, I'm going to describe just a single viewpoint, looking from the eyes of a Tetronian at some specific object in the scene. I'll describe the 4D objects in terms of the shapes of their 3D projections onto the Tetronian's retina.
I. Indoor scene
Looking from the eyes of a Tetronian sitting at his desk in his study, here's what he sees. The wall opposite him appears as a cube at the center of his field of vision. Four of the remaining 5 walls appear as frustums emanating from this cube; the 5th wall is behind him and thus unseen. There's a painting hung on this far wall, which appears as a cuboid somewhere on the upperleft back region of the wall's cubic surface; there's some random 3D objects depicted inside the cuboid of this picture. Below the cube of the far wall is another frustum, the image of the floor. A large part of this frustum is obscured by another brown frustum: the far end of his desk. On the desk is a writing pad, which appears as a white frustum inside the brown frustum, with some 3D curves drawn on it.
Now, on the left and front frustums (two of the 4 side walls connected to the far wall), there are frustum-shaped cutouts: the images of the two windows of the room. There's a crudely-conical shape in the cutout of the front frustum, which is truncated by the faces of the frustum: this is the image of the partially obscured mountain visible through this window. There's a horizontal plane dividing the left window's frustum into two halves; the top half is bluish -- the image of the sky outside -- and the bottom half is green -- the image of a flat grass field outside.
In the right frustum (the 4th side wall) there's a tall frustum cutout that reaches to the floor: this is the image of the doorway exiting the room. The door itself is currently not visible, because it opens outwards into the corridor beyond, and it's currently fully open. In the doorway's frustum image, a cuboid-shaped wall is visible: this is the far wall of the corridor that's partially visible from the desk. The remaining volume of the doorway's frustum is filled by triangular prisms: the one on top of the cuboid image of the wall is the partially-obscured image of the corridor's ceiling; the one below the cuboid is the partially-obscured image of the floor of the corridor. The two remaining ones in front and behind the cuboid are the partially-obscured images of two other corridor walls that are visible from the desk (this last part is a uniquely 4D phenomenon: in 3D, we can only ever see one corridor wall from this viewpoint).
Now, above the frustum-shaped image of the desk, somewhere off to the side, is a hemisphere: this is the image of a 4D ball lying on the floor behind the desk; it's partly obscured by the desk.
The Tetronian's arms are resting on the desk; they appear as truncated cones (or cylinders with unequal top/bottom radii, if you wish) emanating from the bottom of the projection volume, and extending diagonally about halfway to the top face of the frustum image of the desk.
II. Outdoor scene
All that description of indoor objects is getting a bit boring -- there are too many tesseractic shapes (which show up as cubes, frustums, and prisms in the projection image), which get a bit too "boxy" after a while. So now the Tetronian decides to get some fresh air outside. He walks out of the house, in the direction of the mountain described earlier, and looks outward in that direction.
Since the house is behind him, it is currently not visible. Instead, he's looking at the distant mountain, which appears as a roughly conical shape filling the center of his field of vision. There are many smaller cones arranged around the base of this big cone: these are the lower peaks and hills in front of the mountain. Some of them are incomplete cones that appear to have been "eaten out" by other cones that overlap their volumes. These are hills that lie behind, and are therefore partly obscured, by other hills in front of them.
From the bottom of the projection volume, there's a wide cone that covers most of the bottom area, but quickly tapers to a point above, somewhat spiralling as it goes. This is the image of the trail that leads to the mountain. Partway up this spiralling cone is a flattened tube shape that branches off and extends to the front of the projection volume. This is a side-trail that branches off the main one, leading somewhere else. Another branch occurs a little farther up the main trail, leading off to the left of the projection volume. This is a second side-trail that leads in another direction. Below these branches, there's a curious torus-shaped trail that encircle the main trail, but not connected to it. This is a crude jogging track not far from the Tetronian's house, that people use for exercise every now and then. Thanks to the extra dimension available, there's no need to put it off to the side of the main trail; it's more convenient to build it around the trail for easier accessibility. It's not connected to the main trail but can be reached by walking across the grassy area the lies between them.
Now, the entire projection volume has two halves, divided by a horizontal plane. This is the (literal!) horizon of the landscape. It is interrupted by the images of the mountain and hills in the middle (they lie closer to than the horizon and therefore obscure it). The upper half is bluish -- the image of the sky; and the lower half is green toward the bottom, but become brownish near the horizon -- the image of the ground, which is grassy near the Tetronian's house, but gradually become more rocky as you approach the mountain and hills. There's a small, partial sphere that sits on the images of the mountain and hills like a half-buried glowing crystal ball: this is the image of the setting sun, which is beginning to descend toward the horizon, partially behind the mountain. On the opposite side of the mountain's image, there's a dark region in the ground that extends away from the globe: this is the 3D shadow of the mountain cast by the sun behind it upon the ground.
In the upper half of the projection image are some amorphous greyish blobs -- these are the images of 4D clouds. If one looks carefully, one will notice that some blobs have been "carved out" by other blobs, some bigger, some smaller -- the "carved" blobs are clouds that are farther away in the 4th direction than the clouds corresponding to the blobs that carve it.
Around the fringes of the horizon, there's a band of vertical cylinders that are tall at the edges of the projection volume, but shrink to a short height as you move toward the center; they are capped by amorphous green blobs on top. These are trees in a forest that gird the mountain and hills. The taller part are trees near where the Tetronian is standing; the shorter part are trees farther away (and closer to the mountain). It is tempting to say that the forest surrounds the mountain, but that's not strictly true because it only goes around the mountain in a roughly toroidal region around the base of the mountainous area; the closest 3D analogue would be *two* forests on either side of a mountain -- but in 4D, it's possible for a single forest to extend around the sides of the mountain while still leaving an unforested swath of land in front of it.
III. Looking at the house
Argh, this is taking way to long to write down... maybe later.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
Thank you for your reply quickfur, that was quite a detailed explanation.
There is a question I have though with regards to the viewing axes available in 4D space.
In 3D space there is the X, Y and Z axes. In 4D space, there is also the W axis available, but I'm still trying to understand exactly how that fits into a 4D'ers viewpoint.
The way you describe things in your post, that 4th axis gets put into the same visual image for the 4D being as the other 3, but is there another possibility?
Is there any other way that a 4D'er might see and comprehend things?
Let's say he looks forward along Z, with X as the right/left and Y as the up/down.
The W axis needs to be put in there, but the problem is that it is also perpendicular to the X and Y axes, so it is going "away" from him in another direction, but also in a direction that is perpendicular to X and Y too.
It would be a direction that is in a 4D volume "in behind" the X and Y axes, so it might be "hidden" from view as long as one is looking along Z.
In 4D space though, there is a full circle of extra directions with the W axis available, but can one look in all those directions at once?
In another thread you said:
So there would be a way, in 4D, for a 4D'er to keep looking at the same thing, and keep his head pointing up, and feet facing down, but be able to see the same thing from other directions in that 4D space?
But would that necessarily be an "all at once view", (as your original post in the thread implies) or could it possibly be a step by step change of orientational view, depending on how his brain might process it?
When you say you can "spin your body around" in 4D does that imply that a 4D'er would have to "spin his directional focusing viewpoint around" while still looking at the same thing and standing on the same spot, in order to see in those other directions?
There is a question I have though with regards to the viewing axes available in 4D space.
In 3D space there is the X, Y and Z axes. In 4D space, there is also the W axis available, but I'm still trying to understand exactly how that fits into a 4D'ers viewpoint.
The way you describe things in your post, that 4th axis gets put into the same visual image for the 4D being as the other 3, but is there another possibility?
Is there any other way that a 4D'er might see and comprehend things?
Let's say he looks forward along Z, with X as the right/left and Y as the up/down.
The W axis needs to be put in there, but the problem is that it is also perpendicular to the X and Y axes, so it is going "away" from him in another direction, but also in a direction that is perpendicular to X and Y too.
It would be a direction that is in a 4D volume "in behind" the X and Y axes, so it might be "hidden" from view as long as one is looking along Z.
In 4D space though, there is a full circle of extra directions with the W axis available, but can one look in all those directions at once?
In another thread you said:
quickfur wrote:So even while facing the same direction in 4D (and keeping your head pointing up and feet on the floor), you still have 4 distinct orientations you can be in. Or, put another way, you can spin your body around in 4D while standing on the same spot, and facing the same direction, without changing the latter.
So there would be a way, in 4D, for a 4D'er to keep looking at the same thing, and keep his head pointing up, and feet facing down, but be able to see the same thing from other directions in that 4D space?
But would that necessarily be an "all at once view", (as your original post in the thread implies) or could it possibly be a step by step change of orientational view, depending on how his brain might process it?
When you say you can "spin your body around" in 4D does that imply that a 4D'er would have to "spin his directional focusing viewpoint around" while still looking at the same thing and standing on the same spot, in order to see in those other directions?
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: 4D Tetronion Viewing 4D Surroundings
Things will become considerably easier to understand if we consider how one sees the world to begin with.
Our eyes actually don't see 3D at all. What we see are 2D projections of the 3D world around us. So even though the world has 3 cardinal directions, our eyes can only see two at a time; the third is collapsed in the process of projection. Let's make it more concrete. Suppose, for simplicity's sake, that our retina can be contained in a square centered on the XY plane, having 4 corners at (±1,±1). Let's say we're standing upright with our eyes at the origin, and looking straight forward in the +Z direction (that is, in the direction of (0,0,1)), and the +Y direction (0,1,0) is up. +X is on our right, and -X is on our left. So given some object in 3D space at (x,y,z), it would get projected to our retina as (x/d, y/d, 0), where d = √(x2 + y2 + z2). Notice that the last coordinate is zero, meaning that our retina cannot perceive 3D depth; it can only see width along the lateral dimension (+X and -X), and height along the vertical dimension (+Y and -Y). Notice that the direction of the object along the X and Y axes are retained in the projected image.
Now, in order to give a frame of reference about the orientation of things, let's say we take some sticks and glue them together into a 3D cross shape, such that there's a stick pointing in each of the +X, -X, +Y, -Y, +Z, -Z directions -- six directions in total. Let's say we put this cross directly in front of us, at (0,0,10). What would we see? Well, the projection causes the +Z and -Z directions to collapse, so we don't see a 6-armed cross, but a 4-arm cross, with the +X arm projected to our right, the -X arm projected to our left, the +Y arm upwards, and the -Y arm downwards.
Now suppose we are still looking in the same direction, but no longer standing upright, but lying on our side, with our feet pointing in the +X direction. How would the cross appear to us? Again, the +Z and -Z directions collapse to a point, so we only see a 4-arm cross. This time, however, the 4 arms appear to us in a different orientation than before: now the +X arm appears to point downwards, the -X arm appears to point upwards, and the +Y arm appears to point to our right, and the -Y arm appears to point to our left. Note that we are still looking in the same direction, and the image is still the same, except rotated by 90°. So the effect of rotating our body sideways, so that our feet point in -X instead of -Y, is to rotate the projection image in our retina.
Carrying this to 4D now, in 4D there are 8 directions: +W, -W, +X, -X, +Y, -Y, and +Z, -Z. Suppose for simplicity that we are looking in the +W direction, standing upright. Suppose we now make a 4D cross out of sticks, with one stick pointing in each of the 8 directions. So how would this cross appear to a 4D being? Well, just like in 3D our eyes can only see 2D, the eyes of a 4D being can only see 3D. So the +W and -W arms are collapsed into a point, and the 4D being sees not an 8-armed cross, but only a 6-armed cross, with an arm in each of the +X, -X, +Y, -Y, +Z, -Z directions. Let's say +Y is still the vertical direction. So +Y points up, -Y points down, +X points right, -X points left, +Z points front (not front as in where the 4D being is facing, but front as in the front part of the 3D retina centered on the origin), and -Z points back (not behind the 4D being, but in the back of the 3D retina).
If the 4D being were to lie on its side with feet pointing in +X instead of -Y, then, of course, the arms of the 4D cross would appear rotated by 90°: the +X arm now appears pointing down, the -X arm appears pointing up, the +Y arm appears pointing right, and the -Y arm appears pointing left. The +Z and -Z arms still point the same way, but they have (apparently) rotated around their own axis (appearing as if they spun around 90° in-place). This is analogous to the 3D situation, where lying on your side causes the projection image to turn on its side as well.
However, in 4D there's another kind of orientation change that doesn't occur in 3D. This is if the 4D being continues standing upright, with feet pointing in the -Y direction, head in the +X direction, and he continues looking in the same direction: +W. However, he spins his body in-place such that his right arm now points in +Z instead of +X, and his left arm now points in -Z instead of -X. What happens then? Well, the projection image of the 4D cross will still have its +Y and -Y arms pointing up and down, and its +W and -W arms are still collapsed to a point. But now, the other 4 horizontal arms have rotated: the +X arm now appears in the back of the retina instead of the right, and the -X arm now appears in the front (again, these are not back/front as in behind or in front of the 4D being, but rather a description of where they appear in the 3D retina of the 4D being's eye). The +Z arm now appears to the right and the -Z arm now appears to the left. The projection image hasn't changed, you see, but it has rotated 90° in the horizontal plane.
Our eyes actually don't see 3D at all. What we see are 2D projections of the 3D world around us. So even though the world has 3 cardinal directions, our eyes can only see two at a time; the third is collapsed in the process of projection. Let's make it more concrete. Suppose, for simplicity's sake, that our retina can be contained in a square centered on the XY plane, having 4 corners at (±1,±1). Let's say we're standing upright with our eyes at the origin, and looking straight forward in the +Z direction (that is, in the direction of (0,0,1)), and the +Y direction (0,1,0) is up. +X is on our right, and -X is on our left. So given some object in 3D space at (x,y,z), it would get projected to our retina as (x/d, y/d, 0), where d = √(x2 + y2 + z2). Notice that the last coordinate is zero, meaning that our retina cannot perceive 3D depth; it can only see width along the lateral dimension (+X and -X), and height along the vertical dimension (+Y and -Y). Notice that the direction of the object along the X and Y axes are retained in the projected image.
Now, in order to give a frame of reference about the orientation of things, let's say we take some sticks and glue them together into a 3D cross shape, such that there's a stick pointing in each of the +X, -X, +Y, -Y, +Z, -Z directions -- six directions in total. Let's say we put this cross directly in front of us, at (0,0,10). What would we see? Well, the projection causes the +Z and -Z directions to collapse, so we don't see a 6-armed cross, but a 4-arm cross, with the +X arm projected to our right, the -X arm projected to our left, the +Y arm upwards, and the -Y arm downwards.
Now suppose we are still looking in the same direction, but no longer standing upright, but lying on our side, with our feet pointing in the +X direction. How would the cross appear to us? Again, the +Z and -Z directions collapse to a point, so we only see a 4-arm cross. This time, however, the 4 arms appear to us in a different orientation than before: now the +X arm appears to point downwards, the -X arm appears to point upwards, and the +Y arm appears to point to our right, and the -Y arm appears to point to our left. Note that we are still looking in the same direction, and the image is still the same, except rotated by 90°. So the effect of rotating our body sideways, so that our feet point in -X instead of -Y, is to rotate the projection image in our retina.
Carrying this to 4D now, in 4D there are 8 directions: +W, -W, +X, -X, +Y, -Y, and +Z, -Z. Suppose for simplicity that we are looking in the +W direction, standing upright. Suppose we now make a 4D cross out of sticks, with one stick pointing in each of the 8 directions. So how would this cross appear to a 4D being? Well, just like in 3D our eyes can only see 2D, the eyes of a 4D being can only see 3D. So the +W and -W arms are collapsed into a point, and the 4D being sees not an 8-armed cross, but only a 6-armed cross, with an arm in each of the +X, -X, +Y, -Y, +Z, -Z directions. Let's say +Y is still the vertical direction. So +Y points up, -Y points down, +X points right, -X points left, +Z points front (not front as in where the 4D being is facing, but front as in the front part of the 3D retina centered on the origin), and -Z points back (not behind the 4D being, but in the back of the 3D retina).
If the 4D being were to lie on its side with feet pointing in +X instead of -Y, then, of course, the arms of the 4D cross would appear rotated by 90°: the +X arm now appears pointing down, the -X arm appears pointing up, the +Y arm appears pointing right, and the -Y arm appears pointing left. The +Z and -Z arms still point the same way, but they have (apparently) rotated around their own axis (appearing as if they spun around 90° in-place). This is analogous to the 3D situation, where lying on your side causes the projection image to turn on its side as well.
However, in 4D there's another kind of orientation change that doesn't occur in 3D. This is if the 4D being continues standing upright, with feet pointing in the -Y direction, head in the +X direction, and he continues looking in the same direction: +W. However, he spins his body in-place such that his right arm now points in +Z instead of +X, and his left arm now points in -Z instead of -X. What happens then? Well, the projection image of the 4D cross will still have its +Y and -Y arms pointing up and down, and its +W and -W arms are still collapsed to a point. But now, the other 4 horizontal arms have rotated: the +X arm now appears in the back of the retina instead of the right, and the -X arm now appears in the front (again, these are not back/front as in behind or in front of the 4D being, but rather a description of where they appear in the 3D retina of the 4D being's eye). The +Z arm now appears to the right and the -Z arm now appears to the left. The projection image hasn't changed, you see, but it has rotated 90° in the horizontal plane.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
Thank you for that explanation quickfur.
Man, you really go all out to explain and I really appreciate that.
I'm still wondering about an aspect of a 4D'ers visualization though that I was asking about in my previous post but I'm still not sure about.
I'll try to rephrase the question, coming from another angle.
Take this 2D Necker Cube:

Now, because we have a knowledge of 3D, we can turn the orientation of that perceived 3D cube around into 2 different positions, with the red dot being "inside" the box or "outside" the box.
Do you think there is a possible 3D Necker Cube for 4D'ers?
According to your post, they see in 3D.
Based on their knowledge of 4D, can they turn the orientation of their perceived 3D viewpoint around into different positions? How many?
Man, you really go all out to explain and I really appreciate that.
I'm still wondering about an aspect of a 4D'ers visualization though that I was asking about in my previous post but I'm still not sure about.
I'll try to rephrase the question, coming from another angle.
Take this 2D Necker Cube:

Now, because we have a knowledge of 3D, we can turn the orientation of that perceived 3D cube around into 2 different positions, with the red dot being "inside" the box or "outside" the box.
Do you think there is a possible 3D Necker Cube for 4D'ers?
According to your post, they see in 3D.
Based on their knowledge of 4D, can they turn the orientation of their perceived 3D viewpoint around into different positions? How many?
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: 4D Tetronion Viewing 4D Surroundings
The Necker Cube is an illusion that is unrelated to the kind of orientation changes I was talking about. The Necker cube illusion is caused by the visual ambiguity introduced by collapsing one of the dimensions during the scene-to-eye projection.
The orientation changes I refer to is when the entire projection image rotates in-place (e.g., turn your head sideways while looking at a cube, and you see the cube in a sideways orientation). In 3D, because our eyes see in 2D, there is only one possible such rotation: rotating the 2D region around the eye-to-scene axis. In 4D, the retina sees a 3D image, so it can rotate in at least 3 principal ways (about the 3 axes of its 3D volume), many more if you count oblique rotations. Among these, one in particular stands out, because it leaves the vertical axis unchanged, so it has no direct analogue in 3D because in 3D, all such orientation changes also change the vertical axis. This particular orientation change in 4D spins the image around the vertical axis without changing the vertical itself. It's like a horizontal analogue of the 3D "turn your head sideways" orientation change. This change preserves chirality, so there is no inversion of sense such as what happens in the Necker cube illusion. The two are definitely distinct, because mathematically, it is impossible for a rotation to produce a mirror-image, because a rotation is the product of two reflections, whereas making a mirror-image is a single reflection -- reflections are "odd" and rotations are "even". It is possible to compose two odd transformations to make an even one, but no combination of even transformations will ever become odd (unless you compose it with an odd transformation to begin with).
The orientation changes I refer to is when the entire projection image rotates in-place (e.g., turn your head sideways while looking at a cube, and you see the cube in a sideways orientation). In 3D, because our eyes see in 2D, there is only one possible such rotation: rotating the 2D region around the eye-to-scene axis. In 4D, the retina sees a 3D image, so it can rotate in at least 3 principal ways (about the 3 axes of its 3D volume), many more if you count oblique rotations. Among these, one in particular stands out, because it leaves the vertical axis unchanged, so it has no direct analogue in 3D because in 3D, all such orientation changes also change the vertical axis. This particular orientation change in 4D spins the image around the vertical axis without changing the vertical itself. It's like a horizontal analogue of the 3D "turn your head sideways" orientation change. This change preserves chirality, so there is no inversion of sense such as what happens in the Necker cube illusion. The two are definitely distinct, because mathematically, it is impossible for a rotation to produce a mirror-image, because a rotation is the product of two reflections, whereas making a mirror-image is a single reflection -- reflections are "odd" and rotations are "even". It is possible to compose two odd transformations to make an even one, but no combination of even transformations will ever become odd (unless you compose it with an odd transformation to begin with).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
quickfur wrote:The Necker Cube is an illusion that is unrelated to the kind of orientation changes I was talking about. The Necker cube illusion is caused by the visual ambiguity introduced by collapsing one of the dimensions during the scene-to-eye projection.
Could this same type of collapse happen to a 4D'er viewing 4D matter?
Could that result in one of the viewing dimension axes collapsing because of a visual ambiguity?
In another post you said:
quickfur wrote:This is interesting because as long as the radius is not too far below the 3D thickness of the object, then it behaves "normally", but once its radius becomes too small, it has the risk of "falling over" and acquiring strange properties. So there is a size scale at which things start to turn strange (i.e., 3D effects start to show up). Does this remind you of the real world?Macroscopic objects behave "normally", but once you get down past a certain size, things start to act strangely. Conceivably, this is because objects smaller than a certain size starts to exhibit extra-dimensional properties.
And indeed, this is the idea behind "curled up" dimensions and string theory. When the object is big enough, you don't see anything strange because only their 3D properties are manifested. They are too big to "fall over" in the extra, confined dimensions. But when things get small enough, then the effects of the additional dimensions start to show up. Now they can "fall over" in the extra dimensions, and when we try to interpret the effects from our 3D-centric point of view, we find them really strange. But if we interpret them as the effect of having extra dimensions to "fall" or "rotate" in, then a lot of these effects become quite mundane. That's one of the neat things about string theory.
Is it possible that in a 4D world, the particles that make it up are just like you describe above?
Could it be that, like looking at a hose from afar, it only looks like a line, when a 4D'er looks at a particle of matter, he can't see all of the 6 arms of the cross as you described above, but sees less, because of the visual ambiguity?
As more of those 4D particles are added around that particle, what can be actually seen by the 4D'er, with his large scale of vision?
You said "When the object is big enough, you don't see anything strange because only their 3D properties are manifested. They are too big to "fall over" in the extra, confined dimensions."
Could that possibly be the same for a 4D'er?
Let's say that all of that is a possibility.
For a thought experiment, let's say it's true for a 4D'er.
So then, that 4D'er would see less than a 3D "flat" view of what is in front of him (not seeing a large scale 6-armed cross), let's say he'd only see a 2D plane, (seeing a large scale 4-armed cross).
Now, because he would actually be in 4D space, and made up of 4D matter himself, there would be more existing real directions within space than he would be aware of with his limited 2D plane of vision, but he would have access to those real directions that would exist for him.
His vision would see a 3D world around him, but there is a question about how all those other existing directions of space around him would be perceived by his brain.
You mentioned earlier that "The Necker cube illusion is caused by the visual ambiguity introduced by collapsing one of the dimensions during the scene-to-eye projection."
How would this affect what the 4D'er sees of his 4D world, if there is a visual ambiguity introduced by one of the dimensions collapsing because of the particles being so small, thus ambiguous?
What kind of perceived Necker Cube Illusion could result?
I mean, he's kind of "inside" a 3D Necker Cube, which is capable of being seen from different directions within that 4D space, because of that ambiguity caused by the individual particles of matter's dimensions being too small to see individually.
Would this be possible? As a thought experiment.

-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: 4D Tetronion Viewing 4D Surroundings
The Necker cube illusion has nothing to do with particles being big or small. It's an inherent ambiguity in any projection-based sight, that is, any kind of eye that sees based on light reflecting off the surfaces of objects. If you're a dolphin with sonar-sense, you'll have a much different experience.  The reason for the ambiguity is because you're seeing n dimensions with only an (n-1)-dimensional retina, meaning that information about one of the dimensions (depth) is lost, so some projection images can have multiple interpretations that may not necessarily reflect reality.
The reason for the ambiguity is because you're seeing n dimensions with only an (n-1)-dimensional retina, meaning that information about one of the dimensions (depth) is lost, so some projection images can have multiple interpretations that may not necessarily reflect reality.
As for a 4D being confined to a lower-dimensional space -- if he is indeed confined in that way, that means (1) he no longer has access to the extra dimensions of space, since otherwise he's no longer confined ; (2) he is effectively no longer a "4D being" but something lower-dimensional, since all his perception is limited to a lower-dimensional space, and all his movement is also limited thus. So it doesn't matter that he's actually made of 4D (or higher) particles, since in his experience he can never tell the difference. (3) Since he is confined to lower-dimensional space, the effects of 4D (or higher dimensions) such as the reorientation effect I described earlier no longer apply macroscopically; the only way to even begin to notice such effects is to go down to the subatomic level. Nothing in the macroscopic world would behave any differently from a truly lower-dimensional space; it would be as if it were truly only a lower-dimensional space.
; (2) he is effectively no longer a "4D being" but something lower-dimensional, since all his perception is limited to a lower-dimensional space, and all his movement is also limited thus. So it doesn't matter that he's actually made of 4D (or higher) particles, since in his experience he can never tell the difference. (3) Since he is confined to lower-dimensional space, the effects of 4D (or higher dimensions) such as the reorientation effect I described earlier no longer apply macroscopically; the only way to even begin to notice such effects is to go down to the subatomic level. Nothing in the macroscopic world would behave any differently from a truly lower-dimensional space; it would be as if it were truly only a lower-dimensional space.
 The reason for the ambiguity is because you're seeing n dimensions with only an (n-1)-dimensional retina, meaning that information about one of the dimensions (depth) is lost, so some projection images can have multiple interpretations that may not necessarily reflect reality.
The reason for the ambiguity is because you're seeing n dimensions with only an (n-1)-dimensional retina, meaning that information about one of the dimensions (depth) is lost, so some projection images can have multiple interpretations that may not necessarily reflect reality.As for a 4D being confined to a lower-dimensional space -- if he is indeed confined in that way, that means (1) he no longer has access to the extra dimensions of space, since otherwise he's no longer confined
 ; (2) he is effectively no longer a "4D being" but something lower-dimensional, since all his perception is limited to a lower-dimensional space, and all his movement is also limited thus. So it doesn't matter that he's actually made of 4D (or higher) particles, since in his experience he can never tell the difference. (3) Since he is confined to lower-dimensional space, the effects of 4D (or higher dimensions) such as the reorientation effect I described earlier no longer apply macroscopically; the only way to even begin to notice such effects is to go down to the subatomic level. Nothing in the macroscopic world would behave any differently from a truly lower-dimensional space; it would be as if it were truly only a lower-dimensional space.
; (2) he is effectively no longer a "4D being" but something lower-dimensional, since all his perception is limited to a lower-dimensional space, and all his movement is also limited thus. So it doesn't matter that he's actually made of 4D (or higher) particles, since in his experience he can never tell the difference. (3) Since he is confined to lower-dimensional space, the effects of 4D (or higher dimensions) such as the reorientation effect I described earlier no longer apply macroscopically; the only way to even begin to notice such effects is to go down to the subatomic level. Nothing in the macroscopic world would behave any differently from a truly lower-dimensional space; it would be as if it were truly only a lower-dimensional space.- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
quickfur wrote:The Necker cube illusion has nothing to do with particles being big or small. It's an inherent ambiguity in any projection-based sight, that is, any kind of eye that sees based on light reflecting off the surfaces of objects. If you're a dolphin with sonar-sense, you'll have a much different experience.The reason for the ambiguity is because you're seeing n dimensions with only an (n-1)-dimensional retina, meaning that information about one of the dimensions (depth) is lost, so some projection images can have multiple interpretations that may not necessarily reflect reality.
Does smallness not create an ambiguity in itself? Like a hose viewed from a long distance, only an apparent line can be seen, not the curled around dimension.
Just like viewing a wall made out of a hundred hoses, viewed from a long distance away could be seen as only a "flat" wall.
Or a ball made out of rolled up hoses might only be seen as a "flat" circle from a distance.
Close up, the objects can be seen and understood in their real sense, but from a distance, there are different interpretations that one might have of these objects.
So even though our retina sees an object very close up in one instance, that same retina loses a dimension when that object is very far away, or small in another.
Seeing involves the reception of light waves, but there are limits as to the smallness of dimensions that can be interpreted.
Sonar involves the reception of sound waves, but there are limits as to the smallness of dimensions that can be interpreted as well.
Would a dolphin sense the small curled up dimension of the hoses in the wall from a long distance away, or just sense it as a flat wall?
One could make all kinds of detailed objects up close, but from far away, they all are perceived as "flat".
Whatever object that one looks at, one only sees the conglomeration of all of the apparent "flat" surfaces of all of the individual particles put together.
quickfur wrote:As for a 4D being confined to a lower-dimensional space -- if he is indeed confined in that way
I'm not thinking about a 4D being confined to a lower-dimensional space, I'm thinking about a 4D being having access to that 4D space, but being limited in his viewing of that space because of the ambiguity of the tiny particles that make it, and himself up.
We know that ambiguity can cause the loss of the viewing, or sensing, of a dimension.
The lines that make up the 2D Necker Cube can be ambiguous, so there's a loss of dimension, and different orientations to see the perceived cube in.
Could it be similarly so for a 4D'er?
The planes that make up a 3D Necker Cube in his space could be ambiguous (based on the smallness of the particles that make up his space and himself), so there's a loss of dimension, and different orientations to see his perceived space in.
In 3D, two squares share a line.
In 4D, two cubes share a plane, and it is around that plane that a Necker Cube type illusion might appear to a 4D'er.
Would that be possible?
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: 4D Tetronion Viewing 4D Surroundings
Let's not confuse ourselves by conflating the various different things that are going on here.
First, there's the Necker cube illusion, which is caused by a particular configuration of lines having multiple interpretations. The Necker cube is really just one instance of a general phenomenon. If you draw a hexagon with 3 lines that connect opposite corners (so they intersect in the middle), that could be interpreted in a variety of different ways: as a 2D figure (i.e., a hexagon with 3 lines inside), a projection of a cube, a projection of a hexagonal pyramid, or a whole bunch of other things. This has nothing to do with smallness or bigness; the ambiguity is due to the representation of a (possibly) higher-dimensional object in a lower dimensional medium. No matter what the size of the hexagon is, these multiple interpretations exist. Or, to take a more extreme example, say you have a circle with 10cm radius. If you're looking at this circle from a 1 meter distance, it could be interpreted to be a 10cm radius circle 1 meter away, or a planet-sized circle hundreds of thousands of kilometers away. Both project to a similar-sized object, and you can't tell the difference just by the size of the circle alone; you have to take into account circumstantial factors such as light and shade, stereoscopic vision, prior experience (we know the moon is very far away, even it it looks like it's just a few meters behind the trees), etc.. The ambiguity is caused by representing a 3D scene as a 2D projection. It has nothing to do with the size of the object itself.
About the Necker cube illusion itself, though -- a 4D equivalent would be a "Necker tesseract", where the 4D being looks at a transparent tesseract, and the square ridges could be interpreted one of two ways: as lying in front, or lying behind. A 4D being looking at a 3D object will not see any illusions, because the 3D object can be completely and unambiguously represented in his 3D retina.
Second, there's the matter of distant objects having ambiguous shape, not because of the projection itself (mathematically, no matter how far away the tube is, it still has non-zero radius in projection, whereas a mathematical line has zero width), but because of the limited resolution of our retina. Just as the thinnest line you can represent on a computer screen is 1 pixel (you can somewhat go below this by using tricks like antialiasing with greyscale, but that only goes so far), so the thinnest line your eye can discern is 1 retinal cell -- which, incidentally, has far higher resolution than any man-made computer screen thus far. Objects at a distance have unclear shape because their details are too small to be adequately represented by the retina's array of cells (i.e., the eye's "pixels"), not because their shape is inherently ambiguous. Resolution also has nothing to do with loss of dimension; a 3D object that appears as a point because of its distance doesn't suddenly become a lower-dimensional object. It's just that the eye's resolution can't discern its exact shape because of limited resolution. In a mathematical retina with unlimited resolution, there is no dimension loss at all -- it just appears as a very small 2D projection image.
Then there's the matter of 4D orientations, which has nothing to do with any illusions or size ambiguities. It's just a consequence of the extra degree of freedom in 4D making it possible to position your body in many more ways than in 3D. As I've already explained, the only visual effect of this is to rotate the projection image in your retina; it doesn't change what you see. A rotated Necker cube is still a Necker cube, and a rotated non-Necker cube is still a non-Necker cube. It's not any different from standing on your head and seeing the world upside-down -- it's not that the world has turned upside down, or that the directions in 3D space have become "ambiguous", it's just an effect of your body's orientation in space.
Then about the 4D being who only sees in 2D: such a 4D being would be pretty dysfunctional, because a 2D retina is far too inadequate to convey sufficient information about 4D surroundings to allow one to navigate effectively in that space. That's like us trying to navigate in 3D while seeing only a 1D line. Imagine if you were walking around with blinders on both sides of your eyes, each pair of blinders only 0.1mm thick. That is, you can hardly see a thing at all, except two ultrathin lines. You wouldn't even know what you were looking at, since nothing would have any width, and even the slightest turn of your head would completely change what you see through those two lines in such a drastic way that you couldn't tell what part of the new line is connected with what part of the old line. Remember that every direction in an entire 360° of surroundings will give you a completely different slice of the 3D surroundings, and we're not just talking about only 360 directions, because turning even just 0.1° can drastically change what you see. For all you know, you could be looking at a row of LEDs with random colors. Somebody posted a link to the game Auraline some time ago, where you get to experience what it's like having only a 1D retina. Let's just say claustrophobic barely begins to describe the experience, and this is a game set in 2D, the native space for a 1D retina! Now imagine if this barely functional eyesight had to serve in navigating 3D. Being totally lost would be the understatement of the year.
because a 2D retina is far too inadequate to convey sufficient information about 4D surroundings to allow one to navigate effectively in that space. That's like us trying to navigate in 3D while seeing only a 1D line. Imagine if you were walking around with blinders on both sides of your eyes, each pair of blinders only 0.1mm thick. That is, you can hardly see a thing at all, except two ultrathin lines. You wouldn't even know what you were looking at, since nothing would have any width, and even the slightest turn of your head would completely change what you see through those two lines in such a drastic way that you couldn't tell what part of the new line is connected with what part of the old line. Remember that every direction in an entire 360° of surroundings will give you a completely different slice of the 3D surroundings, and we're not just talking about only 360 directions, because turning even just 0.1° can drastically change what you see. For all you know, you could be looking at a row of LEDs with random colors. Somebody posted a link to the game Auraline some time ago, where you get to experience what it's like having only a 1D retina. Let's just say claustrophobic barely begins to describe the experience, and this is a game set in 2D, the native space for a 1D retina! Now imagine if this barely functional eyesight had to serve in navigating 3D. Being totally lost would be the understatement of the year.  You might as well be blind, for the amount of help your sight would give you (i.e., virtually no help at all, except maybe to tell the difference between light and dark). Similarly, a 4D being cursed with a 2D-only eyesight might as well be blind, since the 2D retina can barely even begin to capture the sheer amount of space in 4D, nevermind the objects in it.
You might as well be blind, for the amount of help your sight would give you (i.e., virtually no help at all, except maybe to tell the difference between light and dark). Similarly, a 4D being cursed with a 2D-only eyesight might as well be blind, since the 2D retina can barely even begin to capture the sheer amount of space in 4D, nevermind the objects in it.
Finally, about the size of particles: this has nothing to do with any illusions or size ambiguities or retinas with limited dimension. In everyday life, we don't see any particles at all -- what we see are macroscopic conglomerations of them. Even the smallest speck of dust contains so many particles that billions or trillions barely even begins to describe it. Let's say a particle is the size of a soccer ball, which is about 1 foot in diameter (roughly speaking). Now think about how many soccer balls it would take to fill the entire earth. Now say the Earth is the size of a peppercorn (about 2-3 mm in diameter or so). The size of the solar system, by comparison, would be about half a mile wide. How many earths would it take to fill up the size of the solar system? Now convert that to how many soccerballs it would take to fill up all of these earths. Now let's say the solar system is the size of a grain of sand. Then the size of the Milky Way would be about 100m in diameter. How many solar systems would it take to fill up the entire Milky Way galaxy? Now convert that to the number of soccerballs it would take to fill up the entire galaxy. Guess what? This number is far, far, far, far smaller than the number of particles that exist in the smallest speck of dust that you can see. We're not even close to 0.000001% of the total number of particles that exist in that single speck of dust. Our eyesight is already incapable of seeing anything significantly smaller than that speck of dust, yet the number of particles in it is still a number so large that words fail to describe how many that is! If there's any illusion that might arise from the size of particles, it's all irrelevant to us, because we already can't see anything long before we even get near that size! Or, put another way, any visual effect that we can see must be something so huge relative to the size of particles, that it can't possibly be caused by the size of the particles themselves. (Remember: size of soccerball relative to size of galaxy, and the galaxy is still smaller than the smallest visible speck of dust.) It has to be a macroscopic effect, otherwise we wouldn't be able to notice it in the first place!
We're not even close to 0.000001% of the total number of particles that exist in that single speck of dust. Our eyesight is already incapable of seeing anything significantly smaller than that speck of dust, yet the number of particles in it is still a number so large that words fail to describe how many that is! If there's any illusion that might arise from the size of particles, it's all irrelevant to us, because we already can't see anything long before we even get near that size! Or, put another way, any visual effect that we can see must be something so huge relative to the size of particles, that it can't possibly be caused by the size of the particles themselves. (Remember: size of soccerball relative to size of galaxy, and the galaxy is still smaller than the smallest visible speck of dust.) It has to be a macroscopic effect, otherwise we wouldn't be able to notice it in the first place!
First, there's the Necker cube illusion, which is caused by a particular configuration of lines having multiple interpretations. The Necker cube is really just one instance of a general phenomenon. If you draw a hexagon with 3 lines that connect opposite corners (so they intersect in the middle), that could be interpreted in a variety of different ways: as a 2D figure (i.e., a hexagon with 3 lines inside), a projection of a cube, a projection of a hexagonal pyramid, or a whole bunch of other things. This has nothing to do with smallness or bigness; the ambiguity is due to the representation of a (possibly) higher-dimensional object in a lower dimensional medium. No matter what the size of the hexagon is, these multiple interpretations exist. Or, to take a more extreme example, say you have a circle with 10cm radius. If you're looking at this circle from a 1 meter distance, it could be interpreted to be a 10cm radius circle 1 meter away, or a planet-sized circle hundreds of thousands of kilometers away. Both project to a similar-sized object, and you can't tell the difference just by the size of the circle alone; you have to take into account circumstantial factors such as light and shade, stereoscopic vision, prior experience (we know the moon is very far away, even it it looks like it's just a few meters behind the trees), etc.. The ambiguity is caused by representing a 3D scene as a 2D projection. It has nothing to do with the size of the object itself.
About the Necker cube illusion itself, though -- a 4D equivalent would be a "Necker tesseract", where the 4D being looks at a transparent tesseract, and the square ridges could be interpreted one of two ways: as lying in front, or lying behind. A 4D being looking at a 3D object will not see any illusions, because the 3D object can be completely and unambiguously represented in his 3D retina.
Second, there's the matter of distant objects having ambiguous shape, not because of the projection itself (mathematically, no matter how far away the tube is, it still has non-zero radius in projection, whereas a mathematical line has zero width), but because of the limited resolution of our retina. Just as the thinnest line you can represent on a computer screen is 1 pixel (you can somewhat go below this by using tricks like antialiasing with greyscale, but that only goes so far), so the thinnest line your eye can discern is 1 retinal cell -- which, incidentally, has far higher resolution than any man-made computer screen thus far. Objects at a distance have unclear shape because their details are too small to be adequately represented by the retina's array of cells (i.e., the eye's "pixels"), not because their shape is inherently ambiguous. Resolution also has nothing to do with loss of dimension; a 3D object that appears as a point because of its distance doesn't suddenly become a lower-dimensional object. It's just that the eye's resolution can't discern its exact shape because of limited resolution. In a mathematical retina with unlimited resolution, there is no dimension loss at all -- it just appears as a very small 2D projection image.
Then there's the matter of 4D orientations, which has nothing to do with any illusions or size ambiguities. It's just a consequence of the extra degree of freedom in 4D making it possible to position your body in many more ways than in 3D. As I've already explained, the only visual effect of this is to rotate the projection image in your retina; it doesn't change what you see. A rotated Necker cube is still a Necker cube, and a rotated non-Necker cube is still a non-Necker cube. It's not any different from standing on your head and seeing the world upside-down -- it's not that the world has turned upside down, or that the directions in 3D space have become "ambiguous", it's just an effect of your body's orientation in space.
Then about the 4D being who only sees in 2D: such a 4D being would be pretty dysfunctional,
 because a 2D retina is far too inadequate to convey sufficient information about 4D surroundings to allow one to navigate effectively in that space. That's like us trying to navigate in 3D while seeing only a 1D line. Imagine if you were walking around with blinders on both sides of your eyes, each pair of blinders only 0.1mm thick. That is, you can hardly see a thing at all, except two ultrathin lines. You wouldn't even know what you were looking at, since nothing would have any width, and even the slightest turn of your head would completely change what you see through those two lines in such a drastic way that you couldn't tell what part of the new line is connected with what part of the old line. Remember that every direction in an entire 360° of surroundings will give you a completely different slice of the 3D surroundings, and we're not just talking about only 360 directions, because turning even just 0.1° can drastically change what you see. For all you know, you could be looking at a row of LEDs with random colors. Somebody posted a link to the game Auraline some time ago, where you get to experience what it's like having only a 1D retina. Let's just say claustrophobic barely begins to describe the experience, and this is a game set in 2D, the native space for a 1D retina! Now imagine if this barely functional eyesight had to serve in navigating 3D. Being totally lost would be the understatement of the year.
because a 2D retina is far too inadequate to convey sufficient information about 4D surroundings to allow one to navigate effectively in that space. That's like us trying to navigate in 3D while seeing only a 1D line. Imagine if you were walking around with blinders on both sides of your eyes, each pair of blinders only 0.1mm thick. That is, you can hardly see a thing at all, except two ultrathin lines. You wouldn't even know what you were looking at, since nothing would have any width, and even the slightest turn of your head would completely change what you see through those two lines in such a drastic way that you couldn't tell what part of the new line is connected with what part of the old line. Remember that every direction in an entire 360° of surroundings will give you a completely different slice of the 3D surroundings, and we're not just talking about only 360 directions, because turning even just 0.1° can drastically change what you see. For all you know, you could be looking at a row of LEDs with random colors. Somebody posted a link to the game Auraline some time ago, where you get to experience what it's like having only a 1D retina. Let's just say claustrophobic barely begins to describe the experience, and this is a game set in 2D, the native space for a 1D retina! Now imagine if this barely functional eyesight had to serve in navigating 3D. Being totally lost would be the understatement of the year.  You might as well be blind, for the amount of help your sight would give you (i.e., virtually no help at all, except maybe to tell the difference between light and dark). Similarly, a 4D being cursed with a 2D-only eyesight might as well be blind, since the 2D retina can barely even begin to capture the sheer amount of space in 4D, nevermind the objects in it.
You might as well be blind, for the amount of help your sight would give you (i.e., virtually no help at all, except maybe to tell the difference between light and dark). Similarly, a 4D being cursed with a 2D-only eyesight might as well be blind, since the 2D retina can barely even begin to capture the sheer amount of space in 4D, nevermind the objects in it.Finally, about the size of particles: this has nothing to do with any illusions or size ambiguities or retinas with limited dimension. In everyday life, we don't see any particles at all -- what we see are macroscopic conglomerations of them. Even the smallest speck of dust contains so many particles that billions or trillions barely even begins to describe it. Let's say a particle is the size of a soccer ball, which is about 1 foot in diameter (roughly speaking). Now think about how many soccer balls it would take to fill the entire earth. Now say the Earth is the size of a peppercorn (about 2-3 mm in diameter or so). The size of the solar system, by comparison, would be about half a mile wide. How many earths would it take to fill up the size of the solar system? Now convert that to how many soccerballs it would take to fill up all of these earths. Now let's say the solar system is the size of a grain of sand. Then the size of the Milky Way would be about 100m in diameter. How many solar systems would it take to fill up the entire Milky Way galaxy? Now convert that to the number of soccerballs it would take to fill up the entire galaxy. Guess what? This number is far, far, far, far smaller than the number of particles that exist in the smallest speck of dust that you can see.
 We're not even close to 0.000001% of the total number of particles that exist in that single speck of dust. Our eyesight is already incapable of seeing anything significantly smaller than that speck of dust, yet the number of particles in it is still a number so large that words fail to describe how many that is! If there's any illusion that might arise from the size of particles, it's all irrelevant to us, because we already can't see anything long before we even get near that size! Or, put another way, any visual effect that we can see must be something so huge relative to the size of particles, that it can't possibly be caused by the size of the particles themselves. (Remember: size of soccerball relative to size of galaxy, and the galaxy is still smaller than the smallest visible speck of dust.) It has to be a macroscopic effect, otherwise we wouldn't be able to notice it in the first place!
We're not even close to 0.000001% of the total number of particles that exist in that single speck of dust. Our eyesight is already incapable of seeing anything significantly smaller than that speck of dust, yet the number of particles in it is still a number so large that words fail to describe how many that is! If there's any illusion that might arise from the size of particles, it's all irrelevant to us, because we already can't see anything long before we even get near that size! Or, put another way, any visual effect that we can see must be something so huge relative to the size of particles, that it can't possibly be caused by the size of the particles themselves. (Remember: size of soccerball relative to size of galaxy, and the galaxy is still smaller than the smallest visible speck of dust.) It has to be a macroscopic effect, otherwise we wouldn't be able to notice it in the first place!- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
Thank you for your detailed response quickfur.
I have been working on a reply, but first, I'd like to ask your opinion about this page from Mathematician Alex Bogomolny about the tesseract:
http://www.cut-the-knot.org/ctk/Tesseract.shtml
Specifically, these quotes are of interest to me with regards to this conversation.
"In 4D, a shape can be rotated around a plane."
"It must be understood that in 4D a 3-dimensional cube has neither inside nor outside. All points of a cube are as much exposed in 4D as are the points of a square in 3D."
"Vacuously, in a square there is only 1 square that contains a given edge. In a cube, every edge is shared by 2 squares. In a tesseract, 3 squares meet at every edge. Taken pairwise, squares through the same edge define three cubes. Detecting the three cubes seems akin to shifting a view point when observing the Necker cube."
"I found this observation useful when playing with the applet below. What is it about? Travelling in 4D may have a milder effect on a 3D body than turning it inside out. It may only change its orientation."
I have been working on a reply, but first, I'd like to ask your opinion about this page from Mathematician Alex Bogomolny about the tesseract:
http://www.cut-the-knot.org/ctk/Tesseract.shtml
Specifically, these quotes are of interest to me with regards to this conversation.
"In 4D, a shape can be rotated around a plane."
"It must be understood that in 4D a 3-dimensional cube has neither inside nor outside. All points of a cube are as much exposed in 4D as are the points of a square in 3D."
"Vacuously, in a square there is only 1 square that contains a given edge. In a cube, every edge is shared by 2 squares. In a tesseract, 3 squares meet at every edge. Taken pairwise, squares through the same edge define three cubes. Detecting the three cubes seems akin to shifting a view point when observing the Necker cube."
"I found this observation useful when playing with the applet below. What is it about? Travelling in 4D may have a milder effect on a 3D body than turning it inside out. It may only change its orientation."
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: 4D Tetronion Viewing 4D Surroundings
Hugh wrote:[...]
"In 4D, a shape can be rotated around a plane."
"It must be understood that in 4D a 3-dimensional cube has neither inside nor outside. All points of a cube are as much exposed in 4D as are the points of a square in 3D."
That's correct. Think of it this way: a 2D being confined to the 2D plane would consider that a square has an inside and an outside: the inside is the area surrounded by its 4 edges, and the outside is everything else in the 2D world. The 2D being cannot reach inside the square and pull out a piece of its interior, without first cutting through its edges and tunnelling all the way into where that piece lies, because 2D space does not afford any directions that could allow you to bypass the edges of the square and the stuff that surrounds that piece of the interior. So from a 2Der's point of view, the inside of the square is not exposed to the outside; you cannot reach in and take something out without first breaking a hole through its edges and digging through until you reach that thing.
Also, this square in 2D can only rotate around a point -- because it's confined to 2D space and has no freedom to undergo any other rotation. So in 2D, rotation around a point is the only possibility.
Now consider the very same square, this time immersed in 3D. Does it have an inside or an outside? Not really... well, it does, in the sense that there's a square-shaped area that sits between its 4 edges. But this area is now no longer an "inside", because now, from 3D, you can touch any part of the area without needing to break open its edges and digging through the surrounding material. You can easily cut out a piece of its interior without touching the rest of it.
Furthermore, a square immersed in 3D can rotate not only in the plane that it lies in; it can rotate around its edges, or its diagonals, or any of a whole bunch of different 3D rotational axes. Such rotations are impossible in 2D.
The square itself hasn't changed; the only difference is that it is now immersed in 3D rather than confined to 2D.
Similarly, when we handle a 3D cube in our 3D space, we find that it has an inside and an outside: you cannot reach inside the cube without first breaking through one of its 6 outer faces. And while 3D space affords us many ways to rotate the cube, there is no way to rotate it "around a plane" -- that's a 3D impossibility. However, if this same cube were immersed in 4D space, then things would be different. What we imagine to be its inside now becomes exposed to someone who has access to 4D. A 4D person could reach into (what we think is) the inside of the cube without passing through its 6 faces. The cube could also now rotate "around a plane" -- in a direction that we 3D people cannot perceive nor reach. The cube itself hasn't changed -- these are only the effects of the extra dimension of space that it can now access.
"Vacuously, in a square there is only 1 square that contains a given edge. In a cube, every edge is shared by 2 squares. In a tesseract, 3 squares meet at every edge. Taken pairwise, squares through the same edge define three cubes. Detecting the three cubes seems akin to shifting a view point when observing the Necker cube."
In the context of the page you linked to, the author here is talking about a particular projection of the tesseract, in which one is trying to identify where each of its 8 cells are. The Necker cube illusion here isn't strictly a Necker cube illusion, but a shift in viewpoint because we're trying to "see" cubes that are oriented in 4D space, which causes them to appear in a strange orientation on the screen because normally in 3D, cubes can't have those kinds of orientations. Their actual orientation is actually fixed; there is no real illusion here other than the artificial effect produced by our inability to see them in 4D.
"I found this observation useful when playing with the applet below. What is it about? Travelling in 4D may have a milder effect on a 3D body than turning it inside out. It may only change its orientation."
According to the context of the original page, the author is talking about the possibility of a 3D object getting flipped into its mirror-image in 4D. This is a purely mathematical device -- and comes from an early realization by Möbius, I believe it was, who realized that one could flip a 3D object into its mirror-image by a rigid rotation if only one could access a 4th dimension of space. This is similar to the idea of taking a 2D figure, say the letter R, and flipping it into Я. You can't do this in 2D, because no 2D rotation can do such a flip. But if you could rip the R out of the page, so to speak, then you could spin it around in 3D into Я and then stick it back onto the page.
This says nothing about the physical possibility of flipping, of course: it's merely a mathematical device to illustrate the difference between 2D and 3D, or 3D and 4D. If we really could flip through 4D space, then what happens if we don't perform the full 180° rotation required by the orientation flip, but only a 90° rotation? Then we'd be staring off into the 4th direction, and be in neither orientation! And what about if we got interrupted before we get to the 90° point, say somebody startled us and we're left stuck at 36° from the 3D hyperplane? Now we'd be staring off into 4D in a diagonal direction, and as soon as we tried to move in any of the familiar 3D directions, we'd leave the 3D universe altogether. Since we have no idea how to navigate in 4D space, we'd quickly get lost and be unable to return to the 3D universe -- because even if we did manage to find where it is, we wouldn't know how to rotate ourselves into the right orientation to fit back in!
There's also the question of what we'd see while in the middle of a 180° rotation through 4D that flips our orientation. Clearly, if we really were undergoing such a rotation, then our line-of-sight would be outside the 3D hyperplane between the time that we start the rotation at 0° and the time that we end the rotation at 180°, and so we'd be looking off into 4D space somewhere from 1°, 2°, ..., to ... 178°, 179°. Obviously such a thing would be an absolutely fantastical visual experience of seeing things that don't exist in the 3D universe, and I'd say we'd totally notice it if this happens! Now I can't speak for anybody else, but at least I've never experienced such a thing before, and I'd say that if somebody doesn't experience such a thing, then in all likelihood there isn't any 4D rotation taking place, but it's probably something else.
Also, if somebody was looking at you while you're performing a rotation through 4D, they'd see your body morph and warp in an impossible way, and I'd say they'd totally freak out! Moreover, they won't be any less freaked out after you return to 3D, because they'd see that you've just turned into your mirror-image -- your left hand is now your right hand, and vice versa, and the writing on your shirt has flipped into its mirror-image. (Of course, if I wanted to mess with you, I could secretly swap my wedding ring to my right hand and swap my shirt with another one that has all the writing custom-printed backwards, and perhaps apply some cosmetics to cover up the scar on the right side of my lip and paint its mirror image on the left side, etc.. But I wouldn't be able to do that Terminator morphing thing that a true 4D rotation could do to my body, and I might have forgotten to switch my shoelaces so the kink in the right lace is still on my right shoe, so I probably won't be able to keep up the deception for very long.
 )
)- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 4D Tetronion Viewing 4D Surroundings
Hi quickfur. I really appreciate the time you have spent in your answers in this thread. I’ve mostly been posting in the VRI thread about the latest ways that A.I. has been helping me to understand things in higher dimensions. I’ve always wanted to come back to this thread and give a response, but felt I needed to work on things more.
I asked ChatGPTo1 to look at our conversation in this thread and help me with a response to you, that addresses your points and tries to explain my idea in a better way, that we might be 4D in 4D and that VRIs might be a clue that it may be possible.
ChatGPTo1:
Dear quickfur,
Thank you for your detailed insights into higher-dimensional spaces and how beings might perceive them. Building upon the previous discussions, I’d like to explore how a four-dimensional (4D) being could experience a sudden perceptual flip in their three-dimensional (3D) surroundings—akin to a Necker cube-like Visual Reorientation Illusion (VRI)—where actual North could be perceived where East, South, or West was.
Geometric Explanation of Perceptual Flips in 4D
1. Understanding Rotations in 4D Space
In 3D space, rotations occur around axes (lines), and we have three planes of rotation (XY, XZ, YZ). However, in 4D space, rotations occur around planes, and there are six independent planes of rotation:
• XY Plane
• XZ Plane
• XW Plane
• YZ Plane
• YW Plane
• ZW Plane
This introduces additional degrees of freedom not present in 3D space.
2. The Nature of 4D Rotations
• Double Rotations: In 4D, rotations can occur simultaneously in two orthogonal planes. For example, a rotation can happen in both the XY and ZW planes at the same time.
• Clifford Rotations: A special type of rotation where the rotation angles in two planes are equal. This results in a rotation that is “evenly distributed” across the two planes.
3. Perceptual Framework of a 4D Being
A 4D being perceives their environment through a 3D projection, similar to how we perceive our 3D world via 2D projections on our retinas. Their sensory organs interpret 3D “slices” or cross-sections of the 4D space.
Experiencing a Perceptual Flip
1. Initial Orientation
Let’s define the 4D being’s coordinate axes:
• X-axis: Left-Right
• Y-axis: Up-Down
• Z-axis: Forward-Backward (initially aligned with North-South)
• W-axis: The fourth spatial dimension (perpendicular to X, Y, and Z)
2. Rotation in the XW Plane
Consider a rotation in the XW plane by 90 or 180 degrees:
• Before Rotation:
• The being’s orientation aligns with the standard axes.
• Their perception of directions corresponds to these axes.
• During Rotation:
• The rotation affects both the X (Left-Right) and W dimensions.
• Since the W-axis is not directly perceivable in their 3D cross-section, the effects manifest in their perception of the X-axis.
3. Perceptual Consequences
• After Rotation:
• 90 Degrees Rotation:
• The X-axis (Left-Right) swaps with the W-axis.
• The being’s perception of Left-Right is altered, potentially mapping to directions they cannot directly perceive.
• 180 Degrees Rotation:
• The X-axis inverts its direction.
• What was perceived as “Left” is now “Right,” and vice versa.
• Effect on Other Axes:
• The Y-axis (Up-Down) remains unchanged.
• The Z-axis (Forward-Backward) may also be affected if the rotation includes other planes (e.g., ZW plane).
4. Mapping of Cardinal Directions
• Perceived Shift of North:
• If the rotation causes the being’s Z-axis (initially aligned with North) to align with what was previously their X-axis (East-West), their perception of North shifts to where East or West was.
• This reorientation happens without any physical movement on their part.
5. Analogous to the Necker Cube Illusion
• Ambiguity in Projection:
• Just as the Necker cube flips between two valid 3D interpretations due to ambiguous 2D projections, a 4D being’s brain might interpret ambiguous 3D projections of their 4D environment in multiple ways.
• Perceptual Flip:
• The sudden change in their perception of directions is akin to the Necker cube’s flip between orientations.
Addressing Potential Counterpoints
1. Rotations and Chirality
• As you’ve explained, rotations in 4D cannot produce mirror images or invert chirality.
• The perceptual flip here doesn’t involve a mirror inversion but a re-mapping of directions due to rotation in higher-dimensional planes.
2. Physical vs. Perceptual Changes
• The being isn’t undergoing physical transformations that would result in impossible morphing.
• The change is in their cognitive interpretation of sensory data resulting from rotations in 4D space.
3. Sensory Limitations and Ambiguities
• Even with a 3D retina, a 4D being might experience perceptual ambiguities due to the complexities of interpreting 3D projections of a 4D environment.
• Similar to how we experience VRIs despite accurate sensory input, they might have multiple valid interpretations of their sensory data.
Mathematical Representation
1. Rotation Matrices in 4D
A rotation in the XW plane by angle θ can be represented by the following matrix:
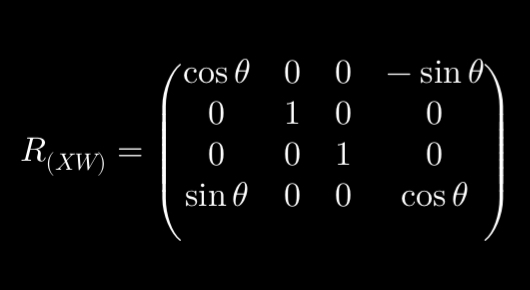
2. Applying the Rotation
• When this matrix is applied to the coordinates of objects in the being’s environment, their positions along the X and W axes change.
• Since the W-axis isn’t directly perceived, changes along this axis affect how the X-axis is represented in their 3D perception.
3. Resulting Perception
• The being’s internal coordinate system has rotated, causing a mismatch between their memory of the environment and their current perception.
• This leads to the sensation that their surroundings have rotated, even though physically, everything remains the same.
Cognitive Interpretation
1. Brain’s Role in Perception
• The brain constructs our perception of space by interpreting sensory inputs.
• In the presence of ambiguous or conflicting information, it might switch between different interpretations.
2. Higher-Dimensional Ambiguity
• The additional degrees of freedom in 4D space introduce more complexity into the sensory data.
• Slight variations or rotations might produce significantly different projections, leading to perceptual flips.
Conclusion
• Perceptual flips in 4D beings can occur due to rotations in higher-dimensional planes, which re-map their internal coordinate system.
• These flips are analogous to the Necker cube illusion but occur in the context of 4D space and 3D perception.
• The phenomenon demonstrates how additional dimensions introduce complexities in perception, even without physical changes in the environment.
I asked ChatGPTo1 to look at our conversation in this thread and help me with a response to you, that addresses your points and tries to explain my idea in a better way, that we might be 4D in 4D and that VRIs might be a clue that it may be possible.
ChatGPTo1:
Dear quickfur,
Thank you for your detailed insights into higher-dimensional spaces and how beings might perceive them. Building upon the previous discussions, I’d like to explore how a four-dimensional (4D) being could experience a sudden perceptual flip in their three-dimensional (3D) surroundings—akin to a Necker cube-like Visual Reorientation Illusion (VRI)—where actual North could be perceived where East, South, or West was.
Geometric Explanation of Perceptual Flips in 4D
1. Understanding Rotations in 4D Space
In 3D space, rotations occur around axes (lines), and we have three planes of rotation (XY, XZ, YZ). However, in 4D space, rotations occur around planes, and there are six independent planes of rotation:
• XY Plane
• XZ Plane
• XW Plane
• YZ Plane
• YW Plane
• ZW Plane
This introduces additional degrees of freedom not present in 3D space.
2. The Nature of 4D Rotations
• Double Rotations: In 4D, rotations can occur simultaneously in two orthogonal planes. For example, a rotation can happen in both the XY and ZW planes at the same time.
• Clifford Rotations: A special type of rotation where the rotation angles in two planes are equal. This results in a rotation that is “evenly distributed” across the two planes.
3. Perceptual Framework of a 4D Being
A 4D being perceives their environment through a 3D projection, similar to how we perceive our 3D world via 2D projections on our retinas. Their sensory organs interpret 3D “slices” or cross-sections of the 4D space.
Experiencing a Perceptual Flip
1. Initial Orientation
Let’s define the 4D being’s coordinate axes:
• X-axis: Left-Right
• Y-axis: Up-Down
• Z-axis: Forward-Backward (initially aligned with North-South)
• W-axis: The fourth spatial dimension (perpendicular to X, Y, and Z)
2. Rotation in the XW Plane
Consider a rotation in the XW plane by 90 or 180 degrees:
• Before Rotation:
• The being’s orientation aligns with the standard axes.
• Their perception of directions corresponds to these axes.
• During Rotation:
• The rotation affects both the X (Left-Right) and W dimensions.
• Since the W-axis is not directly perceivable in their 3D cross-section, the effects manifest in their perception of the X-axis.
3. Perceptual Consequences
• After Rotation:
• 90 Degrees Rotation:
• The X-axis (Left-Right) swaps with the W-axis.
• The being’s perception of Left-Right is altered, potentially mapping to directions they cannot directly perceive.
• 180 Degrees Rotation:
• The X-axis inverts its direction.
• What was perceived as “Left” is now “Right,” and vice versa.
• Effect on Other Axes:
• The Y-axis (Up-Down) remains unchanged.
• The Z-axis (Forward-Backward) may also be affected if the rotation includes other planes (e.g., ZW plane).
4. Mapping of Cardinal Directions
• Perceived Shift of North:
• If the rotation causes the being’s Z-axis (initially aligned with North) to align with what was previously their X-axis (East-West), their perception of North shifts to where East or West was.
• This reorientation happens without any physical movement on their part.
5. Analogous to the Necker Cube Illusion
• Ambiguity in Projection:
• Just as the Necker cube flips between two valid 3D interpretations due to ambiguous 2D projections, a 4D being’s brain might interpret ambiguous 3D projections of their 4D environment in multiple ways.
• Perceptual Flip:
• The sudden change in their perception of directions is akin to the Necker cube’s flip between orientations.
Addressing Potential Counterpoints
1. Rotations and Chirality
• As you’ve explained, rotations in 4D cannot produce mirror images or invert chirality.
• The perceptual flip here doesn’t involve a mirror inversion but a re-mapping of directions due to rotation in higher-dimensional planes.
2. Physical vs. Perceptual Changes
• The being isn’t undergoing physical transformations that would result in impossible morphing.
• The change is in their cognitive interpretation of sensory data resulting from rotations in 4D space.
3. Sensory Limitations and Ambiguities
• Even with a 3D retina, a 4D being might experience perceptual ambiguities due to the complexities of interpreting 3D projections of a 4D environment.
• Similar to how we experience VRIs despite accurate sensory input, they might have multiple valid interpretations of their sensory data.
Mathematical Representation
1. Rotation Matrices in 4D
A rotation in the XW plane by angle θ can be represented by the following matrix:
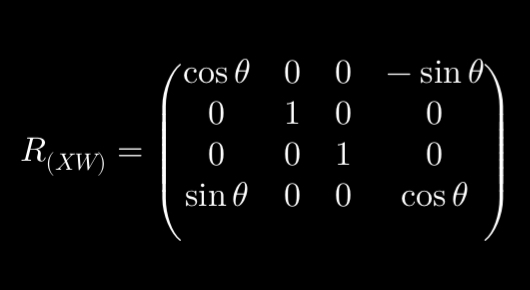
2. Applying the Rotation
• When this matrix is applied to the coordinates of objects in the being’s environment, their positions along the X and W axes change.
• Since the W-axis isn’t directly perceived, changes along this axis affect how the X-axis is represented in their 3D perception.
3. Resulting Perception
• The being’s internal coordinate system has rotated, causing a mismatch between their memory of the environment and their current perception.
• This leads to the sensation that their surroundings have rotated, even though physically, everything remains the same.
Cognitive Interpretation
1. Brain’s Role in Perception
• The brain constructs our perception of space by interpreting sensory inputs.
• In the presence of ambiguous or conflicting information, it might switch between different interpretations.
2. Higher-Dimensional Ambiguity
• The additional degrees of freedom in 4D space introduce more complexity into the sensory data.
• Slight variations or rotations might produce significantly different projections, leading to perceptual flips.
Conclusion
• Perceptual flips in 4D beings can occur due to rotations in higher-dimensional planes, which re-map their internal coordinate system.
• These flips are analogous to the Necker cube illusion but occur in the context of 4D space and 3D perception.
• The phenomenon demonstrates how additional dimensions introduce complexities in perception, even without physical changes in the environment.
My VRI channel: http://youtube.com/channel/UCntWMVVl5wKCx_6CH33_mXg
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
13 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 17 guests
