 by Marek14 » Thu Aug 30, 2012 10:37 pm
by Marek14 » Thu Aug 30, 2012 10:37 pm
Tetrahedral vertices in CRF polychora:
I used Mathematica to check on various tetrahedra for the purpose of CRF polychora:
Even though the list only shows tetrahedral verfs, it already points to several promising areas of research, I think.
They are in form of abcdef, where faces are abd, ace, bcf and def. Allowed faces are:
333, 334, 335, 344, 346, 348, 340, 355, 350, 366, 388, 300, 444, 445, 446, 447, 448, 449, 440, 450, 466, 468, 460, 555 and 566. I'll refer to them with the simplest polyhedron that has them, if there are several.
Seems that euclidean tilings tetrahedra appear here as well (for example 466664). Not sure how to weed them out.
333333: four tetrahedra (verf of pentachoron)
333334: two tetrahedra, two square pyramids
333335: two tetrahedra, two pentagonal pyramids
333344: tetrahedron, two square pyramids, triangular prism
333355: tetrahedron, two pentagonal pyramids, metabidiminished icosahedron
333444: three square pyramids, cube
333445: two square pyramids, pentagonal pyramid, pentagonal prism
334344: tetrahedron, three triangular prisms (verf of tetrahedral prism)
334346: tetrahedron, triangular prism, two triangular cupolas
334348: tetrahedron, triangular prism, two square cupolas
334340: tetrahedron, triangular prism, two pentagonal cupolas
334366: tetrahedron, two triangular cupolas, truncated tetrahedron
334388: tetrahedron, two square cupolas, truncated cube
334434: two square pyramids, two triangular prisms
334436: two square pyramids, two triangular cupolas
334438: two square pyramids, two square cupolas
334430: two square pyramids, two pentagonal cupolas
334444: square pyramid, two triangular prisms, cube
334446: square pyramid, triangular prism, triangular cupola, hexagonal prism
334448: square pyramid, triangular prism, square cupola, octagonal prism
334440: square pyramid, triangular prism, pentagonal cupola, decagonal prism
334466: square pyramid, two triangular cupolas, truncated octahedron
334530: square pyramid, pentagonal pyramid, pentagonal cupola, pentagonal rotunda
334544: pentagonal pyramid, two triangular prisms, pentagonal prism
335355: tetrahedron, three metabidiminished icosahedra
335350: tetrahedron, metabidiminished icosahedron, two pentagonal rotundas
335300: tetrahedron, two pentagonal rotundas, truncated tetrahedron
335450: square pyramid, metabidiminished icosahedron, pentagonal rotunda, diminished rhombicosidodecahedron
335535: two pentagonal pyramids, two metabidiminished icosahedra
335530: two pentagonal pyramids, two pentagonal rotundas
335555: pentagonal pyramid, two metabidiminished icosahedra, dodecahedron
336366: tetrahedron, three truncated tetrahedra (verf of truncated pentachoron)
336444: square pyramid, two triangular cupolas, cube
336446: square pyramid, triangular cupola, truncated tetrahedron, hexagonal prism
336466: square pyramid, two truncated tetrahedra, truncated octahedron
336544: pentagonal pyramid, two triangular cupolas, pentagonal prism
336566: pentagonal pyramid, two truncated tetrahedra, truncated icosahedron
338388: tetrahedron, three truncated cubes (verf of truncated tesseract)
338444: square pyramid, two square cupolas, cube
338448: square pyramid, square cupola, truncated cube, octagonal prism
330300: tetrahedron, three truncated dodecahedra (verf of truncated 120-cell)
330445: square pyramid, pentagonal cupola, pentagonal rotunda, pentagonal prism
330440: square pyramid, pentagonal cupola, truncated dodecahedron, decagonal prism
330450: square pyramid, pentagonal rotunda, truncated dodecahedron, diminished rhombicosidodecahedron
330540: pentagonal pyramid, pentagonal cupola, truncated dodecahedron, diminished rhombicosidodecahedron
330555: pentagonal pyramid, two pentagonal rotundas, dodecahedron
344443: four triangular prisms (verf of 3,3-duoprism)
344444: two triangular prisms, two cubes (verf of 3,4-duoprism)
344445: two triangular prisms, two pentagonal prisms (verf of 3,5-duoprism)
344446: two triangular prisms, two hexagonal prisms (verf of 3,6-duoprism)
344447: two triangular prisms, two heptagonal prisms (verf of 3,7-duoprism)
344448: two triangular prisms, two octagonal prisms (verf of 3,8-duoprism)
344449: two triangular prisms, two enneagonal prisms (verf of 3,9-duoprism)
344440: two triangular prisms, two decagonal prisms (verf of 3,10-duoprism)
34444n: two triangular prisms, two n-gonal prisms (verf of 3,n-duoprism)
344463: two triangular prisms, two triangular cupolas
344464: triangular prism, triangular cupola, cube, hexagonal prism
344466: triangular prism, triangular cupola, hexagonal prism, truncated octahedron
344468: triangular prism, triangular cupola, octagonal prism, truncated cuboctahedron
344460: triangular prism, triangular cupola, decagonal prism, truncated icosidodecahedron
344483: two triangular prisms, two square cupolas
344484: triangular prism, square cupola, cube, octagonal prism
344486: triangular prism, square cupola, hexagonal prism, truncated cuboctahedron
344404: triangular prism, pentagonal cupola, cube, decagonal prism
344405: triangular prism, pentagonal cupola, pentagonal prism, diminished rhombicosidodecahedron
344663: triangular prism, two triangular cupolas, truncated tetrahedron
344664: two triangular cupolas, cube, truncated octahedron
344665: two triangular cupolas, pentagonal prism, truncated icosahedron
344684: triangular cupola, square cupola, cube, truncated cuboctahedron
344883: triangular prism, two square cupolas, truncated cube
345454: triangular prism, metabidiminished icosahedron, two pentagonal prisms
345450: triangular prism, metabidiminished icosahedron, two diminished rhombicosidodecahedra
345404: triangular prism, pentagonal rotunda, pentagonal prism, decagonal prism
345054: pentagonal cupola, metabidiminished icosahedron, pentagonal prism, diminished rhombicosidodecahedron
346444: triangular prism, triangular cupola, cube, hexagonal prism
346446: triangular prism, triangular cupola, hexagonal prism, truncated octahedron
346448: triangular prism, triangular cupola, octagonal prism, truncated cuboctahedron
346440: triangular prism, triangular cupola, decagonal prism, truncated icosidodecahedron
346464: triangular prism, truncated tetrahedron, two hexagonal prisms (verf of truncated tetrahedral prism)
346466: triangular prism, truncated tetrahedron, two truncated octahedra (verf of great rhombated pentachoron)
346468: triangular prism, truncated tetrahedron, two truncated cuboctahedra (verf of great rhombated tesseract)
346460: triangular prism, truncated tetrahedron, two truncated icosidodecahedra (verf of great rhombated 120-cell)
346644: two triangular cupolas, two hexagonal prisms
346646: two triangular cupolas, two truncated octahedra
346648: two triangular cupolas, two truncated cuboctahedra
346640: two triangular cupolas, two truncated icosidodecahedra
346663: two triangular cupolas, two truncated tetrahedra
346664: triangular cupola, truncated tetrahedron, hexagonal prism, truncated octahedron
346844: triangular cupola, square cupola, hexagonal prism, octagonal prism
346846: triangular cupola, square cupola, truncated octahedron, truncated cuboctahedron
346864: square cupola, truncated tetrahedron, hexagonal prism, truncated cuboctahedron
346044: triangular cupola, pentagonal cupola, hexagonal prism, decagonal prism
346046: triangular cupola, pentagonal cupola, truncated octahedron, truncated icosidodecahedron
346064: pentagonal cupola, truncated tetrahedron, hexagonal prism, truncated icosidodecahedron
348444: triangular prism, square cupola, cube, octagonal prism
348446: triangular prism, square cupola, hexagonal prism, truncated cuboctahedron
348484: triangular prism, truncated cube, two octagonal prisms (verf of truncated cubic prism)
348486: triangular prism, truncated cube, two truncated cuboctahedra (verf of great rhombated 24-cell)
348644: triangular cupola, square cupola, hexagonal prism, octagonal prism
348646: triangular cupola, square cupola, truncated octahedron, truncated cuboctahedron
348684: triangular cupola, truncated cube, octagonal prism, truncated cuboctahedron
348846: two square cupolas, two truncated cuboctahedra
348883: two square cupolas, two truncated cubes
348046: square cupola, pentagonal cupola, truncated cuboctahedron, truncated icosidodecahedron
340444: triangular prism, pentagonal cupola, cube, decagonal prism
340445: triangular prism, pentagonal cupola, pentagonal prism, diminished rhombicosidodecahedron
340454: triangular prism, pentagonal rotunda, pentagonal prism, decagonal prism
340404: triangular prism, truncated dodecahedron, two decagonal prisms (verf of truncated dodecahedral prism)
340405: triangular prism, truncated dodecahedron, two diminished rhombicosidodecahedra
340644: triangular cupola, pentagonal cupola, hexagonal prism, decagonal prism
340646: triangular cupola, pentagonal cupola, truncated octahedron, truncated icosidodecahedron
340656: triangular cupola, pentagonal rotunda, truncated icosidodecahedron, truncated icosahedron
340604: triangular cupola, truncated dodecahedron, decagonal prism, truncated icosidodecahedron
340846: square cupola, pentagonal cupola, truncated cuboctahedron, truncated icosidodecahedron
340046: two pentagonal cupolas, two truncated icosidodecahedra
340003: two pentagonal cupolas, two truncated dodecahedra
355553: four metabidiminished icosahedra
355555: two metabidiminished icosahedra, two dodecahedra
355503: two metabidiminished icosahedra, two pentagonal rotundas
355003: metabidiminished icosahedron, two pentagonal rotundas, truncated dodecahedron
356566: metabidiminished icosahedron, truncated tetrahedron, two truncated icosahedra
350054: two pentagonal rotundas, two diminished rhombicosidodecahedra
350003: two pentagonal rotundas, two truncated dodecahedra
366663: four truncated tetrahedra (verf of decachoron)
366664: two truncated tetrahedra, two truncated octahedra (verf of bitruncated tesseract)
366665: two truncated tetrahedra, two truncated icosahedra (verf of bitruncated 120-cell)
368684: truncated tetrahedron, truncated cube, two truncated cuboctahedra [mysterious!]
388883: four truncated cubes (verf of 48-cell)
444444: four cubes (verf of tesseract)
444445: two cubes, two pentagonal prisms (verf of 4,5-duoprism)
444446: two cubes, two hexagonal prisms (verf of 4,6-duoprism)
444447: two cubes, two heptagonal prisms (verf of 4,7-duoprism)
444448: two cubes, two octagonal prisms (verf of 4,8-duoprism)
444449: two cubes, two enneagonal prisms (verf of 4,9-duoprism)
444440: two cubes, two decagonal prisms (verf of 4,10-duoprism)
44444n: two cubes, two n-gonal prisms (verf of 4,n-duoprism)
444450: cube, pentagonal prism, decagonal prism, diminished rhombicosidodecahedron
444466: cube, two hexagonal prisms, truncated octahedron (verf of truncated octahedral prism)
444468: cube, hexagonal prism, octagonal prism, truncated cuboctahedron (verf of truncated cuboctahedral prism)
444460: cube, hexagonal prism, decagonal prism, truncated icosidodecahedron (verf of truncated icosidodecahedral prism)
444555: three pentagonal prisms, dodecahedron (verf of dodecahedral prism)
444566: pentagonal prism, two hexagonal prisms, truncated icosahedron (verf of truncated icosahedral prism)
445544: four pentagonal prisms (verf of 5,5-duoprism)
445540: two pentagonal prisms, two diminished rhombicosidodecahedra
445644: two pentagonal prisms, two hexagonal prisms (verf of 5,6-duoprism)
445640: pentagonal prism, hexagonal prism, diminished rhombicosidodecahedron, truncated icosidodecahedron
445744: two pentagonal prisms, two heptagonal prisms (verf of 5,7-duoprism)
445844: two pentagonal prisms, two octagonal prisms (verf of 5,8-duoprism)
445944: two pentagonal prisms, two enneagonal prisms (verf of 5,9-duoprism)
445044: two pentagonal prisms, two decagonal prisms (verf of 5,10-duoprism)
445n44: two pentagonal prisms, two n-gonal prisms (verf of 5,n-duoprism)
446466: cube, three truncated octahedra (verf of truncated 24-cell)
446468: cube, truncated octahedron, two truncated cuboctahedra
446566: pentagonal prism, two truncated octahedra, truncated icosahedron (verf of great rhombated 600-cell)
446644: four hexagonal prisms (verf of 6,6-duoprism)
446646: two hexagonal prisms, two truncated octahedra (verf of great prismated decachoron)
446648: two hexagonal prisms, two truncated cuboctahedra (verf of great prismated 48-cell)
446744: two hexagonal prisms, two heptagonal prisms (verf of 6,7-duoprism)
446844: two hexagonal prisms, two octagonal prisms (verf of 6,8-duoprism)
446846: hexagonal prism, octagonal prism, truncated octahedron, truncated cuboctahedron (verf of great prismated tesseract)
446944: two hexagonal prisms, two enneagonal prisms (verf of 6,9-duoprism)
446044: two hexagonal prisms, two decagonal prisms (verf of 6,10-duoprism)
446046: hexagonal prism, decagonal prism, truncated octahedron, truncated icosidodecahedron (verf of great prismated 120-cell)
446n44: two hexagonal prisms, two n-gonal prisms (verf of 6,n-duoprism)
447744: four heptagonal prisms (verf of 7,7-duoprism)
447844: two heptagonal prisms, two octagonal prisms (verf of 7,8-duoprism)
447944: two heptagonal prisms, two enneagonal prisms (verf of 7,9-duoprism)
447044: two heptagonal prisms, two decagonal prisms (verf of 7,10-duoprism)
447n44: two heptagonal prisms, two n-gonal prisms (verf of 7,n-duoprism)
448844: four octagonal prisms (verf of 8,8-duoprism)
448846: two octagonal prisms, two truncated cuboctahedra
448944: two octagonal prisms, two enneagonal prisms (verf of 8,9-duoprism)
448044: two octagonal prisms, two decagonal prisms (verf of 8,10-duoprism)
448n44: two octagonal prisms, two n-gonal prisms (verf of 8,n-duoprism)
449944: four enneagonal prisms (verf of 9,9-duoprism)
449044: two enneagonal prisms, two decagonal prisms (verf of 9,10-duoprism)
449n44: two enneagonal prisms, two n-gonal prisms (verf of 9,n-duoprism)
440044: four decagonal prisms (verf of 10,10-duoprism)
440n44: two decagonal prisms, two n-gonal prisms (verf of 10,n-duoprism)
44nn44: four n-gonal prisms (verf of n,n-gonal duoprism)
44mn44: two m-gonal prisms, two n-gonal prisms (verf of m,n-gonal duoprism)
466664: four truncated octahedra
555555: four dodecahedra (verf of 120-cell)
Tetrahedra that are too large or impossible:
333555, 334300, 334468, 334460, 334533, 334540, 334566, 335533, 338544, 330444, 330544, 344403, 344406, 344604, 344003, 346843, 346043, 348843, 348043, 348044, 340446, 340406, 340844, 340043, 340044, 340053, 350053, 360604, 300003, 446460, 446640, 448566, 448046, 440566, 440046, 450054, 450064, 466665, 466684, 466604, 468864, 468064, 460064, 556566, 566665
Tetrahedra that come out planar:
334433, 346643, 348844, 340045

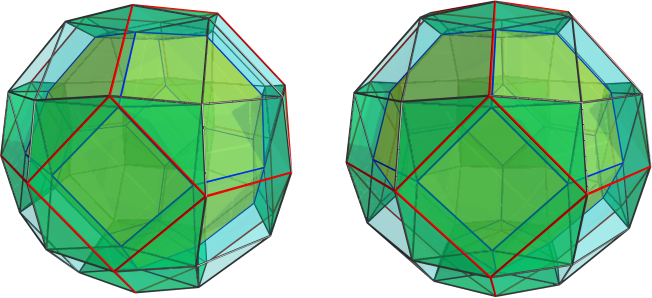




 Or, in my (slightly more readable, if I say so myself) notation, F0100.
Or, in my (slightly more readable, if I say so myself) notation, F0100.

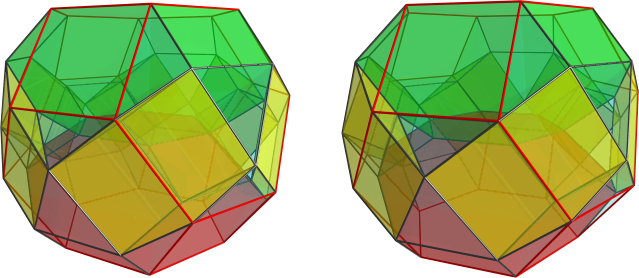
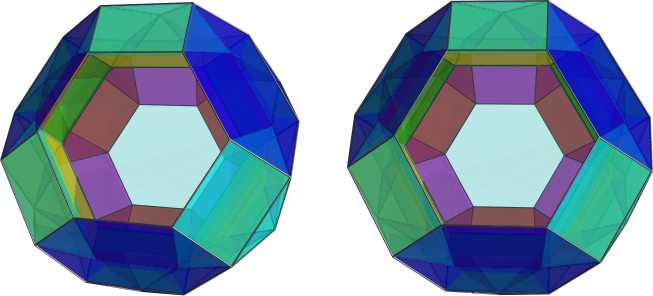

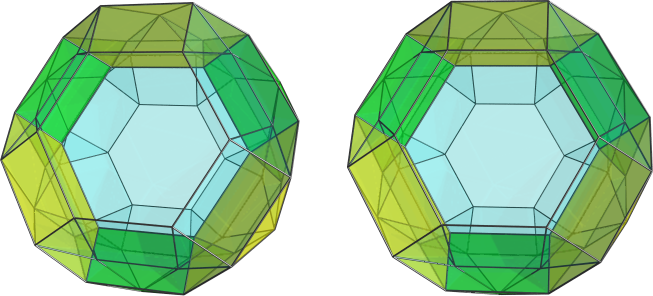

 , a german couple with familyname Blind) in the end 70s and 80s. In fact those did the complete Johnson solid research within higher dimensions. - Just that they extrapolated that definition not in the current sense of CRF, but in the sense of convex regular face
, a german couple with familyname Blind) in the end 70s and 80s. In fact those did the complete Johnson solid research within higher dimensions. - Just that they extrapolated that definition not in the current sense of CRF, but in the sense of convex regular face