Johnsonian Polytopes
Re: Johnsonian Polytopes
P.S. I forgot to add, because I've been working on the code at the same time, the latest release has a new feature in makepoly where you can directly type in coordinates (which can be arbitrary algebraic expressions!) and permutation types, and it will internally generate the points and convert it into Polyhedra format for the convex hull algo. For example, you can now do something like this:
echo 'epacs<0,1,phi>' | makepoly -fperm icosahedron - icosahedron.def
or this:
echo 'apacs<1,1+sqrt(2),1+2*sqrt(2),1+3*sqrt(2)>' | makepoly -fperm omnitruncated_tesseract - omnitesseract.def
This should make it a lot easier to try out new polytopes, you no longer have to hand-edit those cumbersome Polyhedra format files anymore. (Of course, you don't have to use echo, you can put a list of points optionally with permutation types in a file, and specify the filename in place of '-'.)
echo 'epacs<0,1,phi>' | makepoly -fperm icosahedron - icosahedron.def
or this:
echo 'apacs<1,1+sqrt(2),1+2*sqrt(2),1+3*sqrt(2)>' | makepoly -fperm omnitruncated_tesseract - omnitesseract.def
This should make it a lot easier to try out new polytopes, you no longer have to hand-edit those cumbersome Polyhedra format files anymore. (Of course, you don't have to use echo, you can put a list of points optionally with permutation types in a file, and specify the filename in place of '-'.)
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Mrrl wrote:quickfur wrote:[...] Also, I'm more confident now that it is possible to runcinate this rotunda, you will get the same count of rectified dodecahedra, but with pentagonal prisms between them, and the tetrahedra around the top cell become cuboctahedra, and the tetrahedra around the bottom cell become triangular cupola, and the bottom cell is expanded into great rhombicosidodecahedron. It is essentially the diminishing of a cantellated 600-cell (CD diagram is o5x3o3x), some of the cuboctahedra are cut into triangular cupolae.
Yes, I also think that it exists. More, you can cut it in one more level and get great rhombicosidodecahedron|||truncated icosahedron rotundaIt has 12 pentagonal rotunda, 30 pentagonal prisms and 40 triangular cupola as side cells
You're right! So we have at least 3 CRF rotundae (rotundachora?). Icosidodecahedral rotunda, runcinated icosidodecahedral rotunda, and diminished runcinated icosidodecahedral rotunda. (Hmm, I think we need shorter names for them.
 ) I'm going to try to compute coordinates and render them, it shouldn't be too hard since all I need is to find the hyperplane equation parallel to the top of the rotunda, and find depth for cutting.
) I'm going to try to compute coordinates and render them, it shouldn't be too hard since all I need is to find the hyperplane equation parallel to the top of the rotunda, and find depth for cutting.I think we should consider which polyhedra can be diminished into johnson solids by cutting in half, and look for polychora with this kind of cells to see if there's a possibility of creating more non-segmentotopic CRFs.
[...] Like augmentations of something by side cell of segmentotope (that can't be used as base because other side is not parallel to this cell), or, better, combining two segmentotopes by cells (at least one of which is not a base) that have some bichoral angles >90 (like we tried to do with two biantiprasmatic rings). All augmentations can be done after that.
I see. I think the most likely candidates for this kind of "sideways" pasting would be segmentotopes whose top/bottom cells are non-uniform, like rotunda or cupolae, since it's easier to paste stuff onto the side with the larger ridges and still remain convex (like gluing cylinder cut in half vertically, pasting on the cut side can be convex, but pasting on round side can't).
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:[...] I'm going to try to compute coordinates and render them, it shouldn't be too hard since all I need is to find the hyperplane equation parallel to the top of the rotunda, and find depth for cutting.
Alright, I have the coordinates for the icosidodecahedral

Side view:
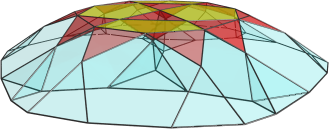
Isn't it so cute? Such a pretty polychoron. I'll find coordinates for the runcinate next. Should be easy 'cos there are cells orthogonal to coordinate axes, so it's just a matter of collecting all vertices of the cantellated 600-cell that have W coordinate with certain values.
Edit: forgot to post coordinates:
- Code: Select all
<(3+sqrt(5))/2, 0, 0, ±1>
<(3+sqrt(5))/2, 0, ±1, 0>
<(3+sqrt(5))/2, ±1, 0, 0>
<(3+sqrt(5))/2, ±(-1+sqrt(5))/4, ±1/2, ±(1+sqrt(5))/4>
<(3+sqrt(5))/2, ±1/2, ±(1+sqrt(5))/4, ±(-1+sqrt(5))/4>
<(3+sqrt(5))/2, ±(1+sqrt(5))/4, ±(-1+sqrt(5))/4, ±1/2>
<(2+sqrt(5))/2, 0, ±(-1+sqrt(5))/4, ±(5+sqrt(5))/4>
<(2+sqrt(5))/2, ±(-1+sqrt(5))/4, ±(5+sqrt(5))/4, 0>
<(2+sqrt(5))/2, ±(5+sqrt(5))/4, 0, ±(-1+sqrt(5))/4>
<(2+sqrt(5))/2, ±(-1+sqrt(5))/4, ±(1+sqrt(5))/4, ±(1+sqrt(5))/2>
<(2+sqrt(5))/2, ±(1+sqrt(5))/4, ±(1+sqrt(5))/2, ±(-1+sqrt(5))/4>
<(2+sqrt(5))/2, ±(1+sqrt(5))/2, ±(-1+sqrt(5))/4, ±(1+sqrt(5))/4>
<(2+sqrt(5))/2, ±(1+sqrt(5))/4, ±1, ±(3+sqrt(5))/4>
<(2+sqrt(5))/2, ±1, ±(3+sqrt(5))/4, ±(1+sqrt(5))/4>
<(2+sqrt(5))/2, ±(3+sqrt(5))/4, ±(1+sqrt(5))/4, ±1>
<(3+3*sqrt(5))/4, 0, ±1/2, ±(3+sqrt(5))/4>
<(3+3*sqrt(5))/4, ±1/2, ±(3+sqrt(5))/4, 0>
<(3+3*sqrt(5))/4, ±(3+sqrt(5))/4, 0, ±1/2>
<(3+3*sqrt(5))/4, ±(1+sqrt(5))/4, ±(1+sqrt(5))/4, ±(1+sqrt(5))/4>
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Alright, here's the runcinated icosidodecahedral rotunda:
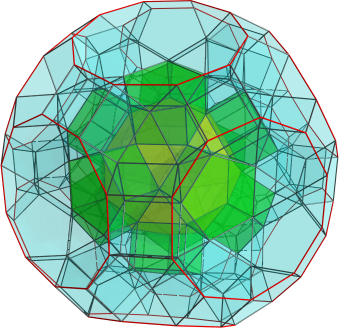
And a nice side view:
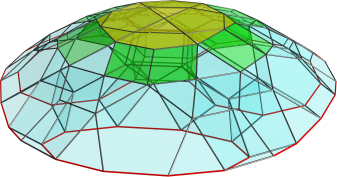
Isn't this a beautiful 4D rotunda?
I'll post the coordinates later, in a separate file (this beauty has a lot of vertices).

And a nice side view:

Isn't this a beautiful 4D rotunda?
I'll post the coordinates later, in a separate file (this beauty has a lot of vertices).
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Post OFF files too, please 

- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:Post OFF files too, please
Here:
Icosidodecahedral rotunda
Runcinated icosidodecahedral rotunda
Sorry, my .off convertor doesn't know how to import povray colors, so you're still getting the randomized per type color assignments.
![Pleased :]](./images/smilies/pleased.gif)
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Marek14 wrote:Post OFF files too, please
Here:
Icosidodecahedral rotunda
Runcinated icosidodecahedral rotunda
Sorry, my .off convertor doesn't know how to import povray colors, so you're still getting the randomized per type color assignments.
Doesn't matter, Stella's recoloring works fine

EDIT: It seems to me that the runcinated cupola could be further split into two shapes: if the cuboctahedra are cut in half, you can replace half of them, the 12 top pentagonal prisms and the icosidodecahedron with a truncated icosahedron.
Last edited by Marek14 on Sat Nov 26, 2011 4:42 pm, edited 1 time in total.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
quickfur wrote:Hmph. You are using a pre-release version of scons, you know that, right?I've tested on SCons 1.0.0 and everything builds fine. But no matter. I've made a different version of the SConscript specifically for you, so install the new sources here:
http://eusebeia.dyndns.org/polyview/polyview-3.0pre-3568.tar.gz
and instead of running 'scons', run 'scons -f SConscript.0.97'. (You only need to do this in the main directory; i've removed the offending rule from the proglib subdir because that file isn't even used anymore anyway, just leftover junk from long ago.)
That's very kind of you, but unfortunately the proglib script still gives the same error.

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Keiji wrote:[...] That's very kind of you, but unfortunately the proglib script still gives the same error.
Alright, this is getting on my nerves. Don't worry, I found a tarball of scons 0.97 and i've just figured out how to run it in my environment. So now I have a way of testing it myself.
 I'm determined to fix this. Just give me a bit of time.
I'm determined to fix this. Just give me a bit of time. 
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Alright, try this:
http://eusebeia.dyndns.org/polyview/polyview-3.0pre-3574.tar.gz
After testing with SCons 0.97, I realized that it has some rather nasty bugs (that have since been fixed in 1.0.0, but no matter). But I discovered a workaround for said bugs. So in both the proglib and main directories, you want to run 'scons -f SConstruct.0.97' instead of just 'scons'. This should work this time, I've actually tested it with SCons 0.97. I've even checked that parallel building works fine (insert -j2 or -j4 or however many processes you want... it's fun to watch ).
).
http://eusebeia.dyndns.org/polyview/polyview-3.0pre-3574.tar.gz
After testing with SCons 0.97, I realized that it has some rather nasty bugs (that have since been fixed in 1.0.0, but no matter). But I discovered a workaround for said bugs. So in both the proglib and main directories, you want to run 'scons -f SConstruct.0.97' instead of just 'scons'. This should work this time, I've actually tested it with SCons 0.97. I've even checked that parallel building works fine (insert -j2 or -j4 or however many processes you want... it's fun to watch
 ).
).- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Marek14 wrote:[...] EDIT: It seems to me that the runcinated cupola could be further split into two shapes: if the cuboctahedra are cut in half, you can replace half of them, the 12 top pentagonal prisms and the icosidodecahedron with a truncated icosahedron.
Yes, mrrl already realized this (see his post earlier in this topic). The result can be considered a
 So we have at least 3 rotundae in 4D.
So we have at least 3 rotundae in 4D.Last edited by quickfur on Sat Nov 26, 2011 6:22 pm, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Coordinates of 4.109. It is some kind of 4-ring (there are point, square, octagon, gyrated square in 4 parallel planes):
0,0,0,-1
±1,±1,1,0
±sqrt(2),0,-1,0
0,±sqrt(2),-1,0
±(1+sqrt(2)),±1,0,1
±1,±(1+sqrt(2)),0,1
It has two square cupolae, two square pyramids and 8 triangular prisms as cells.
I wonder what happens if we replace 3-rd and 4-th lines by single ±1,±1,-1,0 (rotate the second square back). Is there a chance for it to remain CRF? Or some edges will be of length sqrt(2).
0,0,0,-1
±1,±1,1,0
±sqrt(2),0,-1,0
0,±sqrt(2),-1,0
±(1+sqrt(2)),±1,0,1
±1,±(1+sqrt(2)),0,1
It has two square cupolae, two square pyramids and 8 triangular prisms as cells.
I wonder what happens if we replace 3-rd and 4-th lines by single ±1,±1,-1,0 (rotate the second square back). Is there a chance for it to remain CRF? Or some edges will be of length sqrt(2).
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
quickfur wrote:Yes, mrrl already realized this (see his post earlier in this topic). The result can be considered a rhombicosidodecahedral rotunda.So we have at least 3 rotundae in 4D.
Actually we have only two rotunda: runcinated icosidodecahedral rotunda is a chain of rhombicosidodecahedral rotunda and icosidodecadron||rhombicosidodecahedron segmentotope. With some recombined side cells, but we should not afraid such things.
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Here is the truncated icosahedral rotunda (or buckyball rotunda for short  ):
):

And side-view:
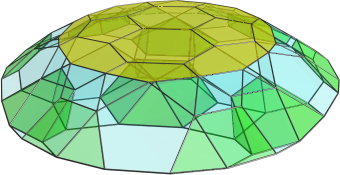
And for Marek: H011_rotunda.off
 ):
):
And side-view:

And for Marek: H011_rotunda.off

- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Mrrl wrote:Coordinates of 4.109. It is some kind of 4-ring (there are point, square, octagon, gyrated square in 4 parallel planes):
0,0,0,-1
±1,±1,1,0
±sqrt(2),0,-1,0
0,±sqrt(2),-1,0
±(1+sqrt(2)),±1,0,1
±1,±(1+sqrt(2)),0,1
It has two square cupolae, two square pyramids and 8 triangular prisms as cells.
I wonder what happens if we replace 3-rd and 4-th lines by single ±1,±1,-1,0 (rotate the second square back). Is there a chance for it to remain CRF? Or some edges will be of length sqrt(2).
Just tested it. I got uneven edge lengths, 2 and 3.2906575520 (unidentified).

- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
And here is the original 4-ring:

Looks like Keiji's gyro square cupolic ring, with the square antiprism replaced by a gyrated pyramid that forms prisms with the original square pyramids. Interesting construction... I wonder if analogous structure exists for pentagonal cupolic rings?
EDIT: another way to think about it, is a gyro- coupling of two square pyramid cupolae (i.e. configuration of square pyramid with 4 prisms and 1 cupola).

Looks like Keiji's gyro square cupolic ring, with the square antiprism replaced by a gyrated pyramid that forms prisms with the original square pyramids. Interesting construction... I wonder if analogous structure exists for pentagonal cupolic rings?
EDIT: another way to think about it, is a gyro- coupling of two square pyramid cupolae (i.e. configuration of square pyramid with 4 prisms and 1 cupola).
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
I realized that I can use the section function in Stella to systematically go through all convex uniform polychora and identify the possible cupolas/rotundas/pyramids, as well as diminishings.
Of course, most of them will be known...
So...
octahedral pyramid (half of hexadecachoron)
octahedral cupola (half of icositetrachoron)
cubic pyramid (vertex cut from icositetrachoron, changing neighbouring octahedra into square pyramids)
icosahedral pyramid (vertex cut from 600-cell)
octahedron||truncated octahedron (half of truncated hexadecachoron, equatorial octahedra cut into square pyramids)
icosahedral rotunda (icosahedron cut from truncated 600-cell, not a segmentochoron: 1 icosahedron, 20 truncated tetrahedra, 12 pentagonal pyramids and 1 truncated icosahedron)
triangular prismatic pyramid and triangular wedge (rectified pentachoron can be cut into these two segmentochora)
tetrahedral cupola (tetrahedron cut off rectified tesseract, if two opposite tetrahedra are cut, segmentochoron 1-1-0||0-1-1 results)
cuboctahedral cupola (cuboctahedron cut off rectified icositetrachoron)
icosidodecahedral rotunda (icosidodecahedron cut off rectified 120-cell)
For rectified 600-cell, three shapes result by cutting off an icosahedral cell. One layer results in icosahedral cupola (1 icosahedron, 20 octahedra, 12 pentagonal pyramids, 1 icosidodecahedron), second layer results in icosidodecahedral copula (1 icosidodecahedron, 20 octahedra, 12 pentagonal antiprisms, 30 square pyramids, 1 rhombicosidodecahedron), but both layers can be taken together into extended icosahedral cupola (1 icosahedron, 40 octahedra, 12 gyroelongated pentagonal pyramids, 30 square pyramids, 1 rhombicosidodecahedron)
pentagonal prismatic pyramid (vertex cut off rectified 600-cell
octahedron||truncated tetrahedron (octahedron cut off small rhombated pentachoron, the rest of the polychoron forms segmentochoron truncated tetrahedron||cuboctahedron
triangle||hexagonal prism (triangular face (cuboctahedron/cuboctahedron) cut off small rhombated pentachoron)
rhombicuboctahedron||truncated cube (rhombicuboctahedron cut off small rhombated tesseract)
square||octagonal prism (square face (rhombicuboctahedron/rhombicuboctahedron) cut off small rhombated tesseract)
cuboctahedron||truncated cube (cuboctahedron cut off small rhombated icositetrachoron)
cutting off second layer of vertices results in truncated cube||great cuboctahedron
cutting both at once will result in a shape consisting of 1 cuboctahedron, 6 elongated square cupolas, 20 triangular prisms (8 + 12), 8 triangular cupolas and 1 great cuboctahedron
rhombicosidodecahedral cupola (rhombicosidodecahedron cut off small rhombated 120-cell)
pentagon||decagonal prism (pentagon cut off small rhombated 120-cell)
icosidodecahedron||truncated icosahedron (icosidodecahedron cut off small rhombated 600-cell)
rhombicosidodecahedral rotunda formed by next layer of small rhombated 600-cell
runcinated icosidodecahedral rotunda, formed by connecting of previous two
truncated tetrahedron||truncated octahedron (truncated tetrahedron cut off prismatorhombated pentachoron)
the rest of the body gives a shape made of 1 cuboctahedron, 4 truncated tetrahedra, 6 hexagonal prisms, 4 triangular prisms, 4 triangular cupolas and 1 truncated cuboctahedron. I suspect it might be possible to glue these two parts of prismatotruncated pentachoron together the "wrong way", so that the the triangular cupolas will be joined to hexagonal prisms and truncated tetrahedra to triangular cupolas instead of combining the cupolas to form cuboctahedra. Not sure if the joins won't blend (into augmented truncated tetrahedra and/or elongated triangular cupolas), but either way, it should be a possible shape!
Prismatotruncated tesseract has an "equatorial region" formed by great cuboctahedral prism and two caps, each of them being formed by 1 rhombicuboctahedron, 6 cubes, 12 hexagonal prisms, 8 truncated tetrahedra, 6 square cupolas and 1 great cuboctahedron.
Prismatotruncated hexadecachoron has caps as truncated cube||great cuboctahedron
Prismatotruncated icositetrachoron has caps as truncated octahedron||great cuboctahedron
Prismatotruncated 120-cell has nonsegmentochoric caps which take 3 layers of vertices. They consist of 1 rhombicosidodecahedron, 12 pentagonal prisms, 20 truncated tetrahedra, 30 hexagonal prisms, 12 pentagonal cupolas and 1 great icosidodecahedron.
Prismatotruncated 600-cell has segmentochoric caps as truncated dodecahedron||great icosidodecahedron.
Small prismated decachoron can be cut in two halves which are tetrahedron||cuboctahedron. It might be possible to glue them together the wrong way.
Small prismated tesseract can be cut in two cube||rhombicuboctahedron and an equatorial rhombicuboctahedral prism.
Small prismated 120-cell has caps formed by dodecahedron||rhombicosidodecahedron.
Small prismated icositetrachoron has caps formed by octahedron||cuboctahedron.
Sorry for hard-to-read list, I was writing as I was discovering
Note that some small rhombated polychora have two different ways of diminishing. Small rhombated 120-cell, in particular, can have either rhombicosidodecahedra removed, which removes 30 triangular prisms and 20 octahedra, diminishes 12 rhombicosidodecahedra around it, and adds 1 great icosidodecahedron, or it can have a pentagon removed, which removes five triangular prisms, cuts in half 5 octahedra, diminishes two rhombicosidodecahedra and adds a decagonal prism. And both types of diminishing can be used at once! That will be a lot of shapes.
Of course, most of them will be known...
So...
octahedral pyramid (half of hexadecachoron)
octahedral cupola (half of icositetrachoron)
cubic pyramid (vertex cut from icositetrachoron, changing neighbouring octahedra into square pyramids)
icosahedral pyramid (vertex cut from 600-cell)
octahedron||truncated octahedron (half of truncated hexadecachoron, equatorial octahedra cut into square pyramids)
icosahedral rotunda (icosahedron cut from truncated 600-cell, not a segmentochoron: 1 icosahedron, 20 truncated tetrahedra, 12 pentagonal pyramids and 1 truncated icosahedron)
triangular prismatic pyramid and triangular wedge (rectified pentachoron can be cut into these two segmentochora)
tetrahedral cupola (tetrahedron cut off rectified tesseract, if two opposite tetrahedra are cut, segmentochoron 1-1-0||0-1-1 results)
cuboctahedral cupola (cuboctahedron cut off rectified icositetrachoron)
icosidodecahedral rotunda (icosidodecahedron cut off rectified 120-cell)
For rectified 600-cell, three shapes result by cutting off an icosahedral cell. One layer results in icosahedral cupola (1 icosahedron, 20 octahedra, 12 pentagonal pyramids, 1 icosidodecahedron), second layer results in icosidodecahedral copula (1 icosidodecahedron, 20 octahedra, 12 pentagonal antiprisms, 30 square pyramids, 1 rhombicosidodecahedron), but both layers can be taken together into extended icosahedral cupola (1 icosahedron, 40 octahedra, 12 gyroelongated pentagonal pyramids, 30 square pyramids, 1 rhombicosidodecahedron)
pentagonal prismatic pyramid (vertex cut off rectified 600-cell
octahedron||truncated tetrahedron (octahedron cut off small rhombated pentachoron, the rest of the polychoron forms segmentochoron truncated tetrahedron||cuboctahedron
triangle||hexagonal prism (triangular face (cuboctahedron/cuboctahedron) cut off small rhombated pentachoron)
rhombicuboctahedron||truncated cube (rhombicuboctahedron cut off small rhombated tesseract)
square||octagonal prism (square face (rhombicuboctahedron/rhombicuboctahedron) cut off small rhombated tesseract)
cuboctahedron||truncated cube (cuboctahedron cut off small rhombated icositetrachoron)
cutting off second layer of vertices results in truncated cube||great cuboctahedron
cutting both at once will result in a shape consisting of 1 cuboctahedron, 6 elongated square cupolas, 20 triangular prisms (8 + 12), 8 triangular cupolas and 1 great cuboctahedron
rhombicosidodecahedral cupola (rhombicosidodecahedron cut off small rhombated 120-cell)
pentagon||decagonal prism (pentagon cut off small rhombated 120-cell)
icosidodecahedron||truncated icosahedron (icosidodecahedron cut off small rhombated 600-cell)
rhombicosidodecahedral rotunda formed by next layer of small rhombated 600-cell
runcinated icosidodecahedral rotunda, formed by connecting of previous two
truncated tetrahedron||truncated octahedron (truncated tetrahedron cut off prismatorhombated pentachoron)
the rest of the body gives a shape made of 1 cuboctahedron, 4 truncated tetrahedra, 6 hexagonal prisms, 4 triangular prisms, 4 triangular cupolas and 1 truncated cuboctahedron. I suspect it might be possible to glue these two parts of prismatotruncated pentachoron together the "wrong way", so that the the triangular cupolas will be joined to hexagonal prisms and truncated tetrahedra to triangular cupolas instead of combining the cupolas to form cuboctahedra. Not sure if the joins won't blend (into augmented truncated tetrahedra and/or elongated triangular cupolas), but either way, it should be a possible shape!
Prismatotruncated tesseract has an "equatorial region" formed by great cuboctahedral prism and two caps, each of them being formed by 1 rhombicuboctahedron, 6 cubes, 12 hexagonal prisms, 8 truncated tetrahedra, 6 square cupolas and 1 great cuboctahedron.
Prismatotruncated hexadecachoron has caps as truncated cube||great cuboctahedron
Prismatotruncated icositetrachoron has caps as truncated octahedron||great cuboctahedron
Prismatotruncated 120-cell has nonsegmentochoric caps which take 3 layers of vertices. They consist of 1 rhombicosidodecahedron, 12 pentagonal prisms, 20 truncated tetrahedra, 30 hexagonal prisms, 12 pentagonal cupolas and 1 great icosidodecahedron.
Prismatotruncated 600-cell has segmentochoric caps as truncated dodecahedron||great icosidodecahedron.
Small prismated decachoron can be cut in two halves which are tetrahedron||cuboctahedron. It might be possible to glue them together the wrong way.
Small prismated tesseract can be cut in two cube||rhombicuboctahedron and an equatorial rhombicuboctahedral prism.
Small prismated 120-cell has caps formed by dodecahedron||rhombicosidodecahedron.
Small prismated icositetrachoron has caps formed by octahedron||cuboctahedron.
Sorry for hard-to-read list, I was writing as I was discovering

Note that some small rhombated polychora have two different ways of diminishing. Small rhombated 120-cell, in particular, can have either rhombicosidodecahedra removed, which removes 30 triangular prisms and 20 octahedra, diminishes 12 rhombicosidodecahedra around it, and adds 1 great icosidodecahedron, or it can have a pentagon removed, which removes five triangular prisms, cuts in half 5 octahedra, diminishes two rhombicosidodecahedra and adds a decagonal prism. And both types of diminishing can be used at once! That will be a lot of shapes.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
quickfur wrote:Just tested it. I got uneven edge lengths, 2 and 3.2906575520 (unidentified).
3.2906575520 = sqrt(8+sqrt(8))

quickfur wrote:Looks like Keiji's gyro square cupolic ring, with the square antiprism replaced by a gyrated pyramid that forms prisms with the original square pyramids. Interesting construction... I wonder if analogous structure exists for pentagonal cupolic rings?
I couldn't find pentagonal ring in the list, but there is triangular ring:
- Code: Select all
4.24 tetrahedron || trigonal cupola
height: sqrt(5/8) = 0.790569
circumradius: 1
comments: kind of diminished half-of runcinated-
pentachoron (tetrahedron as
"tetrahedron - trigon" and trigonal cupola as
"cuboctahedron - trigonal cupola")
cells: 2 tetrahedra + 6 trigonal prisms +
2 trigonal cupolae
And one more object that looks like 4-ring:
- Code: Select all
4.16 square pyramid || gyrated cube
height: sqrt(sqrt(8)-1)/2 = 0.676097
circumradius: sqrt((4+sqrt(2))/7) = 0.879465
other names: -
comments: kind of diminished cubic antiprism
(square pyramid as "octahedron - square
pyramid" and cube as "cube - square")
cells: 4+4+4 tetrahedra + 1+1+4 square
pyramids + 1 square antiprism + 1 cube
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Marek14 wrote:I realized that I can use the section function in Stella to systematically go through all convex uniform polychora and identify the possible cupolas/rotundas/pyramids, as well as diminishings.
Sounds tedious, but since you've done the hard work, ok, sure!

[...] truncated tetrahedron||truncated octahedron (truncated tetrahedron cut off prismatorhombated pentachoron)
the rest of the body gives a shape made of 1 cuboctahedron, 4 truncated tetrahedra, 6 hexagonal prisms, 4 triangular prisms, 4 triangular cupolas and 1 truncated cuboctahedron. I suspect it might be possible to glue these two parts of prismatotruncated pentachoron together the "wrong way", so that the the triangular cupolas will be joined to hexagonal prisms and truncated tetrahedra to triangular cupolas instead of combining the cupolas to form cuboctahedra. Not sure if the joins won't blend (into augmented truncated tetrahedra and/or elongated triangular cupolas), but either way, it should be a possible shape!
This reminds me of the runcinated 5-cell: its two halves are tetrahedral cupola, but it's possible to glue it back the "wrong way" so you get a gyrated form of the runcinated 5-cell.
[...] Sorry for hard-to-read list, I was writing as I was discovering
Maybe you can update the wiki page with your discoveries.

Note that some small rhombated polychora have two different ways of diminishing. Small rhombated 120-cell, in particular, can have either rhombicosidodecahedra removed, which removes 30 triangular prisms and 20 octahedra, diminishes 12 rhombicosidodecahedra around it, and adds 1 great icosidodecahedron, or it can have a pentagon removed, which removes five triangular prisms, cuts in half 5 octahedra, diminishes two rhombicosidodecahedra and adds a decagonal prism. And both types of diminishing can be used at once! That will be a lot of shapes.
Yeah, just the 600-cell alone has who knows how many diminishings... once you start counting the other uniform 600-cell family members, i think this one family alone would totally dominate the number of CRFs in 4D.
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Mrrl wrote:[...]
3.2906575520 = sqrt(8+sqrt(8))
yeah i was just using polyview to calculate the edge lengths, didn't bother to do it algebraically from the coordinates myself.

[...] I couldn't find pentagonal ring in the list, but there is triangular ring: [...]
Hmm. Looks like Klitzing's list covers almost all of the easily-constructible CRFs. Time to search for the truly unique ones...
I wonder if there's a general theory that would allow us to search the space of possible CRFs in a sane way. Such as, given 3 polyhedra joined by some faces, compute some kind of "solid angle" value that tells us what other shapes are possible to fit in there. Also, what combinations of solid angles produce a closeable shape. The thing about 4D is that we inherit the 3D johnson solids, some of which have really strange dihedral angles. It would be nice to know what kind of closed shapes can be built from them.
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Marek14 wrote:Of course, most of them will be known...
[...]
icosahedral rotunda (icosahedron cut from truncated 600-cell, not a segmentochoron: 1 icosahedron, 20 truncated tetrahedra, 12 pentagonal pyramids and 1 truncated icosahedron)
This one is new
Marek14 wrote:truncated tetrahedron||truncated octahedron (truncated tetrahedron cut off prismatorhombated pentachoron)
the rest of the body gives a shape made of 1 cuboctahedron, 4 truncated tetrahedra, 6 hexagonal prisms, 4 triangular prisms, 4 triangular cupolas and 1 truncated cuboctahedron.
It will be cuboctahedral rotunda
 I guess that cutting hyperplane goes through the center on pentachoron - and it's splitted in two different bodies!
I guess that cutting hyperplane goes through the center on pentachoron - and it's splitted in two different bodies!Marek14 wrote: I suspect it might be possible to glue these two parts of prismatotruncated pentachoron together the "wrong way", so that the the triangular cupolas will be joined to hexagonal prisms and truncated tetrahedra to triangular cupolas instead of combining the cupolas to form cuboctahedra. Not sure if the joins won't blend (into augmented truncated tetrahedra and/or elongated triangular cupolas), but either way, it should be a possible shape!
We should check if it is convex or not
Marek14 wrote:Prismatotruncated tesseract has an "equatorial region" formed by great cuboctahedral prism and two caps, each of them being formed by 1 rhombicuboctahedron, 6 cubes, 12 hexagonal prisms, 8 truncated tetrahedra, 6 square cupolas and 1 great cuboctahedron.
For me it looks like elongated rhombicuboctahedral prism that has 6-prism cells augmented by (non-CRF) 6-prism||3-prism cupola. And the result somehow gets CRF!
Note that some small rhombated polychora have two different ways of diminishing. Small rhombated 120-cell, in particular, can have either rhombicosidodecahedra removed, which removes 30 triangular prisms and 20 octahedra, diminishes 12 rhombicosidodecahedra around it, and adds 1 great icosidodecahedron, or it can have a pentagon removed, which removes five triangular prisms, cuts in half 5 octahedra, diminishes two rhombicosidodecahedra and adds a decagonal prism. And both types of diminishing can be used at once! That will be a lot of shapes.
Ok, you have it for cantellated tesseract, simplex and 120-cell. This ridge-centered diminishing is very unexpected! Isn't there any example of edge-centered one?
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:Note that some small rhombated polychora have two different ways of diminishing. Small rhombated 120-cell, in particular, can have either rhombicosidodecahedra removed, which removes 30 triangular prisms and 20 octahedra, diminishes 12 rhombicosidodecahedra around it, and adds 1 great icosidodecahedron, or it can have a pentagon removed, which removes five triangular prisms, cuts in half 5 octahedra, diminishes two rhombicosidodecahedra and adds a decagonal prism. And both types of diminishing can be used at once! That will be a lot of shapes.
Ok, you have it for cantellated tesseract, simplex and 120-cell. This ridge-centered diminishing is very unexpected! Isn't there any example of edge-centered one?
I haven't been able to find any. They obviously exist for prisms, though...
Another shape with multiple possible diminishings is rectified 600-cell, where it's possible to diminish by cells (in two stages, no less), AND by vertices (by removing pentagonal prismatic pyramids).
First-stage icosahedral diminishing takes away an icosahedron and twenty octahedra, diminishes twelve other icosahedra and adds an icosidodecahedron. Second-stage icosahedral diminishing removes an icosahedron and 40 octahedra, cuts further 30 octahedra in half, reduces 12 icosahedra to just pentagonal pyramids and adds a rhombicosidodecahedron.
Vertex diminishing cuts five octahedra in half, diminishes two icosahedra and adds a pentagonal prism.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Mrrl wrote:Marek14 wrote:[...]
icosahedral rotunda (icosahedron cut from truncated 600-cell, not a segmentochoron: 1 icosahedron, 20 truncated tetrahedra, 12 pentagonal pyramids and 1 truncated icosahedron)
This one is new [...]
And here's a render:

Side-view:

And for Marek: http://teamikaria.com/hddb/dl/9QE2WR85KFF8GT98S98CTMQCY7.off
I like this one, it's pretty. It's almost a cupola, so i temporarily name it the "icosahedral-truncated icosahedral cupoloid". It's sorta between a cupola and a rotunda.
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
For the cube||icosahedron segmentochoron, how many different ways there are of gluing the two icosahedra together?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:For the cube||icosahedron segmentochoron, how many different ways there are of gluing the two icosahedra together?
Two ways. Two different cubes inscribed in a dodecahedron always have coinciding pair of verices, so projections of cubes to icosahedron space are either the same, or they have two common vertices (and there are only two possible inscribed cubes with the particular vetrex exist).
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Another idea: for the ridge diminishings of cantellated polychora, is it possible to gyrate them? For example, in cantellated 120-cell, after you cut off pentagon||decagonal prism, you could turn it 36 degrees and glue it back on. Triangular prisms would join with square pyramids and two rhombicuboctahedra would become gyrated.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
The three polytopes a3e4o3x contain the same vertices, edges and some of the faces as a3e3a4x, but with the large faces being different.
For example, x3o4o3x is the same as o3xo3o4x, except that the the eight rCO faces of the latter are replaced by octahedron-rCO cupola (ie xx3oo4ox).
This suggests that you could replace or diminish x3o4o3x in several differnet ways, by capping faces of o3x3o4x, (as this has four axies, one gets
1000, 1100, 1110, 1111, 2000, 2100, 2111, 2200, 2210, 2211, 2220, 2221, for which 0000 and 2222 are both uniform.
One can apply this sequence of 12 uniforms to each of x3o4o3x, x3x4o3x, and o3x4o3x.
Moreover, since the first is reversable, one can diminish various combinations of a figure and its inverse.
Likewise, one can take something like x3o3o5o, which offers no fewer than two different diminishings, and apply these in unison. For example, the rings of the GAP that form the great circles of pentagon antiprisms, correspond to pentagons of the icosahedron, the GAP being the para-diminished Icosahedron, or pentagonal antiprism itself. There is still the diminished, the ortho-bi-diminished and tri-diminished cases (with 10, 20 and 30 paps)
One can also replace such a circle with as many as five vertex-diminished clusters, as many ways as one can place shortchords in a decagon.
The order of replacing the x3o4o3x with peaks, applies to the x3o3o5o, since the 24 faces of the snub-24ch, correspond to three sets of the above, each of which can be appiculated in separate. One has eg, 12*3 + 4 = 40 different ways of apiculating the 24ch's icosahedra, which all lead to different johnson-figures,
For example, x3o4o3x is the same as o3xo3o4x, except that the the eight rCO faces of the latter are replaced by octahedron-rCO cupola (ie xx3oo4ox).
This suggests that you could replace or diminish x3o4o3x in several differnet ways, by capping faces of o3x3o4x, (as this has four axies, one gets
1000, 1100, 1110, 1111, 2000, 2100, 2111, 2200, 2210, 2211, 2220, 2221, for which 0000 and 2222 are both uniform.
One can apply this sequence of 12 uniforms to each of x3o4o3x, x3x4o3x, and o3x4o3x.
Moreover, since the first is reversable, one can diminish various combinations of a figure and its inverse.
Likewise, one can take something like x3o3o5o, which offers no fewer than two different diminishings, and apply these in unison. For example, the rings of the GAP that form the great circles of pentagon antiprisms, correspond to pentagons of the icosahedron, the GAP being the para-diminished Icosahedron, or pentagonal antiprism itself. There is still the diminished, the ortho-bi-diminished and tri-diminished cases (with 10, 20 and 30 paps)
One can also replace such a circle with as many as five vertex-diminished clusters, as many ways as one can place shortchords in a decagon.
The order of replacing the x3o4o3x with peaks, applies to the x3o3o5o, since the 24 faces of the snub-24ch, correspond to three sets of the above, each of which can be appiculated in separate. One has eg, 12*3 + 4 = 40 different ways of apiculating the 24ch's icosahedra, which all lead to different johnson-figures,
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Johnsonian Polytopes
wendy wrote:[...] The order of replacing the x3o4o3x with peaks, applies to the x3o3o5o, since the 24 faces of the snub-24ch, correspond to three sets of the above, each of which can be appiculated in separate. One has eg, 12*3 + 4 = 40 different ways of apiculating the 24ch's icosahedra, which all lead to different johnson-figures,
And furthermore, one doesn't have to stick with the 24 apices of the snub 24-cell alone. One could, for example, diminish the 600-cell at an apex that lies between two of the snub 24-cell's icosahedra, leading to a different kind of diminishing. Adding in these other possibilities greatly expand the number of diminishings of the 600-cell (I think mrrl estimated the number to be close to a million).
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:And furthermore, one doesn't have to stick with the 24 apices of the snub 24-cell alone. One could, for example, diminish the 600-cell at an apex that lies between two of the snub 24-cell's icosahedra, leading to a different kind of diminishing. Adding in these other possibilities greatly expand the number of diminishings of the 600-cell (I think mrrl estimated the number to be close to a million).
No, these were closer to 2^100
 but rectified 600-cell (using only one type of diminishing) beats them - there are proven 2^156 different CRFS with estimations up to 2^500
but rectified 600-cell (using only one type of diminishing) beats them - there are proven 2^156 different CRFS with estimations up to 2^500 
Last edited by Mrrl on Mon Nov 28, 2011 7:25 pm, edited 1 time in total.
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:[...] No, these were closer to 2^100but rectified 120-cell (using only one type of diminishing) beats them - there are proven 2^156 different CRFS with estimations up to 2^500
These crazy huge numbers make me think that there must be a lot of "unique" CRFs in 4D... unique as in, not obviously derived from uniform polytopes and not in the set of segmentotopes. There's got to be a large number of these (though probably not as large as the uniform diminishings). We should've found some of them by now!
- quickfur
- Pentonian
- Posts: 3020
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Who is online
Users browsing this forum: No registered users and 31 guests
