The slices in these images should be stacked one atop the other to make a three dimensional cube. In the last image there, the three-dimensional retina is 73x73x14.
Certainly, I can't output an (n-1)-dimensional image for n > 3 without doing something funky. My raytracer can either tile the layers of the volume (as shown above) or output them as a sequence. In the pictures above, the ( x, y ) pixel of the z-th slice is adjacent in the retina to the ( x+1, y ), ( x-1, y ), ( x, y+1 ), and ( x, y-1 ) pixels of the z-th slice. But, it is also adjacent to the ( x, y ) pixel of the (z-1)-th and (z+1)-th slices.
And, yes... my pictures look like 3d-raytraced pictures if you only consider each slice. But, if you look at it as the collection of slices, there is real information to be gained. For example, look at the red sphere above. The part of the red sphere that you can see in the fourth slice from the top is way at the edge of the sphere. The top slice is right at the center of the sphere.
There is no projection from 3d to 2d. There is just the chopping up of the 3-d retina into something that I can present in 2-d since I can't display a 3-d array of pixels let alone a 4-d or 5-d or 6-d one.
So, no.... I don't compute slices of 4-space with 3d hyperplanes. I have an (n-1)-dimensional retina for an n-dimensional scene. I then slice the (n-1)-dimensional retina into 2-dimensional slices.
Have you ever played 3-d tic-tac-toe?
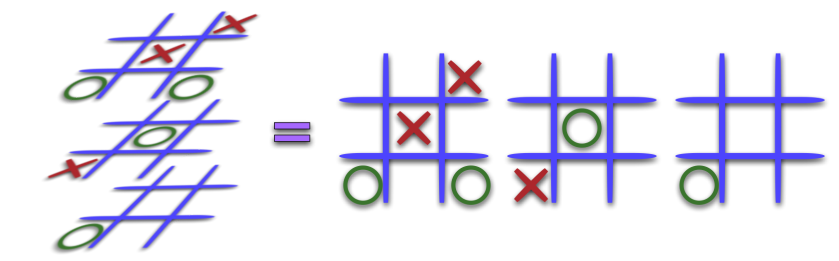
I'm doing the same disassembly of the n-dimensional retina. Here is a composite image meant to mockup what the 3-dimensional retina above would look like. Here, the retina is 512x512x14.

That image doesn't do anything for me. I supposed, it kinda shows the hypersphere shape a little bit, but you can hardly see anything. So, it's not so useful. It's a little more useful if we erase the sky, too.... but that's not the way a retina would work.

And, as I mentioned, the out-of-slice reflection in the above image definitely shows that I'm not working with a slice at a time.
...And, just so there's no confusion, the rendering at the top of the page with the cube, the dodecahedron, and icosahedron is a 3-d scene.....





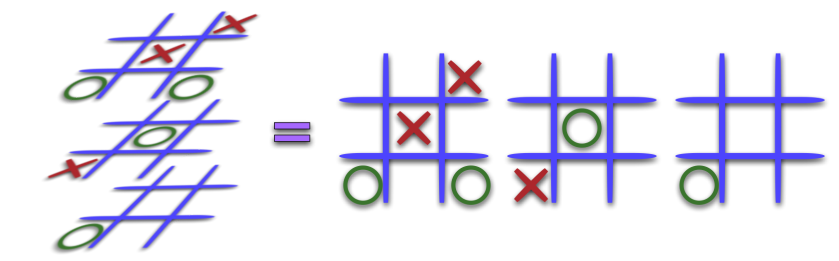




 ) then already convinced me.
) then already convinced me.