According the the theory of relativity, nothing exceeds the speed of light. According to special relativity, any object can consider itself at rest. Say we have two objects approaching each other in a vacuum, each with a velocity of 99.9% the speed of light. At the instant they pass each other, either one of the objects can claim to be at rest, which would make the other object appear to be moving at 199.8% the speed of light (99.9% + 99.9%).
My question is this: Is this even possible? Reality is to the eye of the beholder, and in a vacuum either object could correctly claim to be at rest. If this is true, then the other object is exceeding light speed, which is supposed to be impossible.
One way I saw around this problem is the time dilation at moving at such a speed. Would the dilation reduce the apparent relative speeds to the observers so that, to one another, they don't appear to be approaching so fast?
Curious about this scenario, I wanted to find the apparent dilation between these two objects. If one of the observers claimed to be at rest, what would the passage of time for the other object appear to be? Using
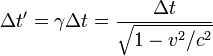
where:
Delta t = "proper time"
Delta t prime = time measured by the other observer
v = relative velocity
c = speed of light
I came up with an undefined number, specifically 1/sq. root of -2.992
Again, I don't know what to make of this. This scenario seems plausible, but the ramifications don't. There would be an undefined apparent time dilation and one object would appear to exceed the speed of light, even though claiming to be at rest is legitimate under special relativity. Is the scenario flawed? Light always moves at the same speed regardless of how it's observed, but these are objects with mass. Ideas / points are most welcome.
EDIT: Maybe the problem is my concept of speed. I pointed out each has a speed of 99.9% the speed of light, but I didn't specify in relation to what. Perhaps it would be better explained as each object approaching a third object exactly between them at 99.9% the speed of light. With that clarification, though, I don't think it changes any of the fundamentals of the problem.

