How to find a CRF

[ubersketch]

TItle says it all.

[Klitzing]

Lots of them are listed on my CRF page, in my CRF list (downloadable Excel), or some on Quickfur's page.

In the past there were just some sporadic finds, say

• via snubbing (alternated facetings),
• via lace prisms (or stacks thereof, aka lace towers, resp. even the closely related segmentotopes) or
• via (partial) Stott expansions.

Based on that student91 once tried to derive a more systematical approach, called the "expanded kaleido facetings", cf. the outline here.

--- rk

[Klitzing]

Just yesterday "found" a further CRF, so far not being listed within my spreadsheet.
So I'll describe it here for you. Thereby you might get a glimps on what we have done all these years before.

I reconsidered ico = 24-cell = x3o4o3o (full F4 sym.) = o3x3o4o (C4 subsym.) = o3x3o *b3o (D4 subsym.).
Esp. its A2 x A2 subsymmetric representation. Here you get as according lace city representation:

Code: Select all

         o3o               -- o3o4o (point)
                    
o3o   q3o   o3q   o3o      -- o3o4x (cube)
                    
   o3q         q3o         -- q3o4o (q-oct)
                    
o3o   q3o   o3q   o3o      -- o3o4x (cube)
                    
         o3o               -- o3o4o (point)


where x=1 (unit edge) and q=sqrt(2).

Now I was interested into its cyclo-tri-diminishing, i.e. in the structure with the lace city

Code: Select all

         o3o         
                    
      q3o   o3q     
                    
   o3q         q3o   
                    
o3o   q3o   o3q   o3o


which, as it turns out, happens to be bounded by 18 square pyramids, 6 octahedra, and 3 cubes.

Just remind yourself that the cells of the 24-cell (ico) are nothing but 24 octahedra. So remaining octahedra and itself diminished octahedra (the square pyramids) shouldn't be surprising here. If you further remember that the vertex figure of ico is nothing but the cube, you'll recognize these as well in the above total as the bases of the 3 withdrawn vertex pyramids.

Finally you should consider the cube in ist axial orientation. Then that one has stacked vertex layers, which are describable as o3o || q3o || o3q || o3o. And just These sequences you could recognize at the outline of the above representation. I.e. those cubes not only are the bases underneath the removed alternate vertices of the outermost hexagon of this projection, they moreover connect vertex-wise at the other, remaining vertices of this very hexagon.

--- rk


PS: this tiny little cutie might be a nice candidate for Quickfur's next "polychoron of the month" rendering (after long)?

PPS: despite the occurances of all these "q" in the above lace cities, all truely being used edges of that "tridiminished icositetrachoron" indeed are all of size x=1. Those q-sized pseudo edges are nothing but the diagonals of squares or of octahedra. Thus this figure is indeed CRF, i.e. convex and regular faced.

[quickfur]

Oooh this would be fun to render! But another time... busy right now with other things.

[quickfur]

BTW, this polychoron being a 24-cell diminishing, it's already counted among the 24-cell diminishings by various people including myself. We just didn't specifically analyze this particular case.

The trigonal symmetry reminds me of the metabathotridiminishing of o3x4o3x, which I've posted about before, it has 3 x4x3x's in a trigonal arrangement wrapping around the polytope. There's also the metatridiminished o3o4x3o, with a trigonal cycle of truncated octahedra in the analogous positions as the x4x3x's in the previous CRF.

These all look to be analogous cuts of the 24-cell family uniforms, with the 24-cell itself yielding to a metatridiminishing, having a trigonal cycle of cubes wrapping around it. It makes one wonder if there are other similar metatridiminishings in the 24-cell family that I haven't enumerated yet (I didn't finish studying all maximal diminishings of the 24-cell family). Note that o3x4o3x admits diminishings at two different depths (hence bathodiminished, to distinguish the deeper cut from the shallower cut), so there's also a metatridiminishing with shallower cuts. In the latter case, I wonder if we might be able to insert another 3 cuts along the orthogonal triangle and have the result turn out CRF? Not sure, have to study it more closely. If it exists, it would correspond with a diminishing along the vertices of an inscribed 3,3-duoprism.

In fact, in my incomplete notes I did note the potential existence of metatridiminishings of x3o4o3x and x3o4x3x, even though I didn't study them in detail to answer the question.

[quickfur]

Alright, here's a render:



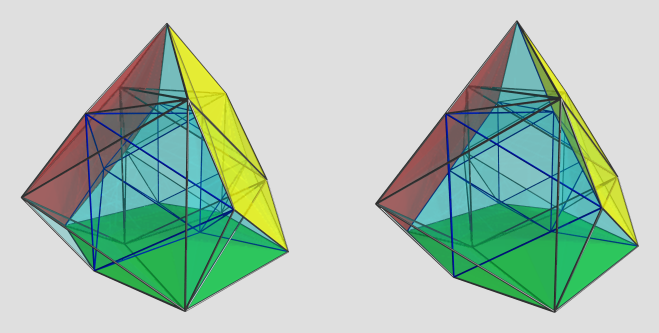
I colored the 3 cubes in red, yellow, and green. It turned out to be surprisingly hard to find a good 4D viewpoint that shows the structure of this little cutie nicely, due to no-clipping causing povray artifacts on ridges that intersect after projection. The blue edges lie on the far side, and the black edges on the near side.

The other cells are somewhat harder to see. You kinda hafta trace their outlines carefully. The square pyramids emanate from the square faces of the 3 cubes (6*3=18 in total), and there's two lines of octahedra sandwiched between the cubes, one on the near side, and the other on the far side, two on each side (for a total of 4) sharing a triangle straddling the 3 cubes, and 2 near the limb of the projection (the near side and far side in the 3D projection envelope). These 6 octahedra lie on the orthogonal great circle to the 3 cubes.

All in all, a very nice maximal diminishing of the 24 cell (no more vertices can be deleted, AFAICT, without making it non-CRF) with 6,3-duoprism subsymmetry.

On another note, I discovered to my chagrin that my list of 24-cell diminishings may have missed this one, due to a false assumption that a tridiminishing must have at least 2 vertices ortho to each other. I need to revisit this again sometime to ascertain if it changes the number of 24-cell diminishings that we posted on the CRF discovery project pages.

[URL]

On a related note, is there any complete listing of the diminishing of simple polychora? I’m having quite a hard time figuring out what polychora can be diminished, and what the possibilities up to symmetry are.

[quickfur]

On a related note, is there any complete listing of the diminishing of simple polychora? I’m having quite a hard time figuring out what polychora can be diminished, and what the possibilities up to symmetry are.

There isn't, because there are too many of them. The 600-cell alone generates at least 300 million distinct CRFs (probably more -- a lot more, my rough guess is at the very least double that amount, or possibly 10+ times more, if not hundreds of times more). Even among the simpler (non-600-cell family) uniform polychora, there are easily hundreds of distinct diminishings. A complete listing would be impractical.

The study I referred to was an attempt to narrow the scope to the maximally-diminished specimens -- diminishings that can't be reduced any further without becoming non-CRF -- because trying to enumerate all diminishings would probably take several lifetimes (if not hundreds of lifetimes ) to complete. Even that study is incomplete, mainly because even maximal diminishings of the 600-cell are so numerous, and the possibilities so numerous, that it's impractical to study by hand. All we have right now is a bunch of specific cases of special interest, usually with high levels of symmetry, or contains unusual cell shapes that are considered interesting. Exhaustive lists are probably infeasible given the huge numbers of shapes. Augmentations of duoprisms alone, for example, number just short of 12 million distinct shapes -- an exhaustive listing would fill multiple libraries of encyclopedias, and that's if you limit yourself to one entry per page (which is not enough to describe many of these shapes!).

And note that these huge numbers are already modulo symmetry operations; if we didn't do that the numbers would be several orders of magnitude larger!

So, studying exhaustive lists is probably not the best approach to learn how these things work. My recommendation is to go to Klitzing's site, learn the CD diagram notation that we use widely here (Coxeter-Dynkin symbols), which give you a very good handle on how to reliably manipulate these things, and then study the large number of very detailed descriptions of individual polytopes on the site. (That will also enable you to understand the derivations we post here, which will be very helpful to learn the methods.) If you're interested in a more visual guide you might want to visit my website, but be aware that I only present the polytopes as-is, I generally don't explain the process by which they are derived. (And also I haven't been able to keep it up to date, I have a lot more data sitting around my PC than I've been able to turn into public-consumable webpages. So many polytopes, so little time! )

[URL]

Well, that kind of defeats my purpose of listing them, doesn't it?

Still, even if polychora derived from high-symmetry forms are far too numerous, I'd like to think that this isn't the case for stuff like the 16-cell or the 24-cell, or their runcinated forms. Is there any listing of the diminishings of these simpler examples?

[Mecejide]

The 16-cell has 2 diminishings: the octahedral pyramid and the square scalene (square pyramidal pyramid).

[quickfur]

I have a list of the diminishings I studied, but they are by no means exhaustive because as I said, there are too many diminishings so i was mainly focusing on finding the maximal diminishings.

Here's a list (note that the counts are for (known) maximal diminishings; there are other intermediate forms not listed):

5-cell family:

Rectified 5-cell (o3o3x3o): 2 maximal diminishings (that I know of), which coincide with Klitzing's segmentochora K4.8.2 and K4.7.2.

Cantellated 5-cell (o3x3o3x): 3 maximal diminishings:
- One coincides with K4.45.1
- Octahedron||truncated tetrahedron (also among Klitzing's segmentochora, but I don't have the K number on hand)
- A CRF obtained by deleting the vertices of two triangles and taking the convex hull. It contains 2 hexagonal prisms joined at their square faces in perpendicular orientation, 4 square pyramids, 1 cuboctahedron, 4 triangular cupola, and 4 triangular prisms. (Maximality not verified)

Runcinated 5-cell (x3o3o3x): 2 diminishings, coinciding with K4.24 and K4.25.

Runcitruncated 5-cell (x3o3x3x): 2 diminishings:
- truncated tetrahedron || truncated octahedron (a segmentochoron)
- what results from cutting off trunc tet||trunc oct from the runcinated 5-cell. I named it the diminished runcinated 5-cell.

Tesseract family:

16-cell: 1 maximal diminishing: the square pyramid pyramid. Non-maximal diminishing: octahedral pyramid.

Rectified 16-cell: the octahedral rotunda/cap (see wiki for pictures).

Rectified tesseract o4o3x3o: 3 diminishings
- tetrahedron || truncated tetrahedron
- deleting the above from the o4o3x3o produces an intermediate form, the diminished rectified tesseract; from this form 2 maximal diminishings can be derived: deleting another tet||trunctet parallel to the first cut produces trunc_tet||trunc_dual_tet, deleting one in a non-parallel hyperplane produces a metabidiminished rectified tesseract (Note: not verified yet)

Runcinated tesseract x4o3o3x: 3 diminishings
- K4.73 (cube||octahedron)
- K4.69 (square cupola prism)
- 4,8-duoprism

Cantellated tesseract x4o3x3o: >6 diminishings
- x4o3x || truncated cube
- truncated cube prism
- octahedral prism || square
- 1,1,(5,8)-tetradiminished cantellated tesseract (tentative name)
- 1,(1,2,3),6-pentadiminished cantellated tesseract (tentative name)
- 8,8-duoprism
- As the names of the 4th and 5th entries imply, there's a whole bunch of intermediate diminishings, and not only so, there's a large number of combinations of cutting-n-pasting 8-prism||square segments in various orientations and combinations that yield various CRFs. These segments can be pasted back gyrated by 45° due the octagonal prism base, and furthermore different patches of the 8,8-duoprism can be created by deleting consecutive such segments from various parts of the cantellated tesseract, and then various bits pasted back on. This is a treasure mine of CRFs.

Runcitruncated 16-cell: 2 maximal diminishings
- x4o3x rotunda/cap
- x4x3x prism

Runcitruncated tesseract x4x3o3x: 2 diminishings
- x4x3x || x4x3o
- bidiminished x4x3o3x

24-cell family:

- 24-cell: 7 diminishings
- 1,1,(5,8)-tetradiminished 24-cell
- 1,(1,2,3),6-pentadiminished 24-cell
- square || cuboctahedron
- octahedron || hexagon (== triangle || gyro triangular cupola)
- cubical pyramid
- tesseract
- metatridiminished 24-cell (that we were just talking about)
- (Note: this list does not include intermediate forms; there are many more non-maximal 24-cell diminishings)

Rectified 24-cell o3o4x3o: 2 diminishings
- cuboctahedron || truncated octahedron
- metatridiminished rectified 24-cell

Cantellated 24-cell o3x4o3x: 4 diminishings
- bidiminished runcitruncated tesseract (o3x4o3x can be considered as an augmentation of the runcitruncated tesseract).
- metabathotridiminished cantellated 24-cell (maximality to be verified) - batho here means a deep cut; there are two depths at which you can diminish the cantellated 24-cell and still remain CRF, so there are plenty of other intermediate forms not listed here.
- cuboctahedron || truncated cube (the piece cut off with a shallow diminishing)
- truncated cube || x4x3x (the other piece cut off from a shallow diminishing to make it a deep diminishing -- and of course, stacking these two pieces produce an intermediate CRF)

Runcinated 24-cell x3o4o3x: ? diminishings
- metatridiminished runcinated 24-cell (to be verified)
- ... probably more, this study wasn't finished

Runcitruncated 24-cell x3o4x3x: ? diminishings
- probably a metatridiminishing (to be verified)
- ... probably more, this study wasn't finished


I didn't include the 120-cell/600-cell family, because as I mentioned there are just way too many of them. But off the top of my head, here's an ad hoc sample of some of them (by no means representative and obviously nowhere near complete, probably doesn't even cover the major categories):

600-cell derivations:
- the 10 lunae of the 600-cell, which together with pentagonal pyramid pyramid gap-filling pieces reconstitute various subsets of the 600-cell, including the hemi-600-cell (a CRF pseudo-bisection of the 600-cell). Large numbers of ad hoc diminishings of each of these combinations.
- the grand antiprism
- the snub 24-cell
- bidex(?) - the chiral CRF consisting of 48 tridiminished icosahedra
- various ad hoc diminishings, like the one with rings of dodecahedra, various wedges
- plus about 300 million other non-adjacent diminishings
- plus an unknown number of adjacent diminishings (that I suspect is much larger than 300 million)

Diminishings of other members of the family:
- spidrox - that awesome chiral baby with 12 rings of alternating pentagonal prisms/antiprisms and 20 twisting rings of square pyramids
- the analogue of spidrox by diminishing the Stott expansion of o5o3x3o, with 12 rings of J90's
- the larger analogue of bidex sporting tridiminished rhombicosidodecahedra instead of tridiminished icosahedra
- various diminishings that sport chiral 5,5-duoprism symmetry (by deleting rings of 5 caps from two orthogonal planes)
- various ad hoc wedges
- a large number of rotunda/cap-like CRF pieces that can be cut off from the uniforms
- bathodiminishings of various higher-order uniforms, and the huge number of combinations when combined with shallower cuts
- the various higher analogues of the 300 diminishings of the 600-cell

There is a vast ocean of CRFs to be found just within the 120-cell family alone; what we have found today is probably only a drop in the ocean.

[username5243]

@quickfur: octahedron || truncaated tetrahedron = K-4.52.

EDIT: Also, K-4.45 is the prism of a triangular cupola, which is not a diminishing of x3o3x3o. I think you meant K-4.51.1 (triangle || hexagonal prism).

[Klitzing]

Today I managed to find a new CRF!

In fact it was "seen" to exist, while revisiting yesterday the list of the EKFs.
There I considered that one:

Code: Select all

                    o2x         o2x                            where
                                N                              F = f+x = ff
          o2o       x2F   f2x   x2F       o2o                  V = 2f
                          E     A         H                    A = F+x = f+2x
                                                               B = V+x = 2f+x = fff
    x2x   f2F       F2o   o2A   F2o       f2F   x2x   
                          F     C         Q     J     
    o2F   F2x       f2A         f2A       F2x   o2F   
                                B         G     K     
                                                      
o2x f2o   x2A      Vo2xB  F2F  Vo2xB      x2A   f2o o2x
                          D     OP        I     L   M 
                                                      
    o2F   F2x       f2A         f2A       F2x   o2F   
                                                      
    x2x   f2F       F2o   o2A   F2o       f2F   x2x   
                                                      
                                                      
          o2o       x2F   f2x   x2F       o2o         
                                                      
                    o2x         o2x                   

which prominently shows 2 lateral bilbiro wedges with "tip" being the position M (and its reflection each), while its base (the bilbiro) would be outlined by the letters J,K,L.

Considering the full symmetry (A1 x A1 x A1 x A1) of this beauty, it occurs further that also the letter P demarks a further "tip" of 2 more bilbiro wedges, the bases of which then are F,B,I.
That is, when chopping off those 4 bilbiro wedges from that EKF, one obtains

Code: Select all

                o2x         o2x                        where
                            N                          F = f+x = ff
      o2o       x2F   f2x   x2F       o2o              V = 2f
                      E     A         H                A = F+x = f+2x
                                                      
x2x   f2F       F2o   o2A   F2o       f2F   x2x
                      F     C         Q     J 
o2F   F2x       f2A         f2A       F2x   o2F
                            B         G     K   
                                              
f2o   x2A       V2x   F2F   V2x       x2A   f2o
                      D     O         I     L 
                                              
o2F   F2x       f2A         f2A       F2x   o2F
                                              
x2x   f2F       F2o   o2A   F2o       f2F   x2x
                                              
                                              
      o2o       x2F   f2x   x2F       o2o     
                                              
                o2x         o2x               

Then I also derived its incidence matrix right now. However it is well too huge to be displayed here. None the less I could provide the cell totals instead. Those read:

• 16+4 = 20 bilbiroes
• 16 paps
• 16+16+8+8 = 48 squippies
• 16 teddis
• 4+4 = 8 tets
• 8+8 = 16 trips

What thus is remarkable about this new find, is that there are just 48 non-Johnsonian cells in contrast to 76 Johnsonian ones!

--- rk

[quickfur]

Don't have the time to parse that lace city right now, but this raises an interesting question: how many CRFs can we find that contains only Johnson solids as cells? Bidex immediately comes to mind (48 tridiminished icosahedra). Any others that we know about?

[Klitzing]

how many CRFs can we find that contains only Johnson solids as cells?

• cute has exactly 12 squippies
• pipt has exactly 10 squippies + 4 peppies
• bidex has exactly 48 teddies

are the ones I'm aware of.

--- rk