axial CRFs

[Klitzing]

Today I reconsidered "mere" multistratic stacks of segmentochora. In especially the bistratic lace towers. - As such, those in generally are not too surprising, just several (here: 2) layers being stacked onto each other. - But my today idea was to look in detail for the sloping angles of the respective lacing cells (wrt. to the parallel bases). The idea was whether there could be found pairs of segmentochora with matching sloping angles in such a way that the lacing cells become corealmic, i.e. can be blended into bistratic Johnsonian solids.

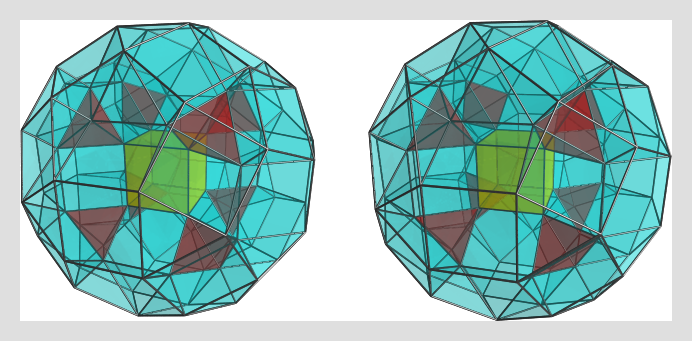
I found these: (did I overlook further ones?)

• oxx3ooo3oox&#xt - cells are: 1 co + 4 tet + 6 trip + 4 etripy (J7)
• oxx3xxx3oox&#xt - cells are: 1 oct + 1 toe + 10 trip + 4 tricu (J3) + 4 etcu (J18)
• oox3ooo4oxx&#xt - cells are: 1 sirco + 8 tet + 12 trip + 6 esquipy (J8)
• oox3xxx4oxx&#xt - cells are: 1 co + 1 girco + 20 trip + 8 tricu (J3) + 6 escu (J19)
• xox3oxo5oox&#xt - cells are: 1 ike + 1 srid + 40 oct + 30 squippy (J1) + 12 gyepip (J11)

--- rk

Edit: strikes out, cf. above.
In fact:

• point||tet||co is not convex:
  the tet-3-tet dihedral angle of point||tet = pen is arccos(1/4) = 75.522488 degrees
  the tet-3-trip dihedral angle of tet||co is arccos(-sqrt(3/8)) = 127.761244 degrees
  thus the sum exceeds 180 degrees; especially they do not sum to 180 degrees exactly, as was needed for those etripies ...
• oct||tut||toe is not convex either:
  the tricu-6-tut dihedral angle of oct||tut is arccos(1/4) = 75.522488 degrees
  the trip-3-tut dihedral angle of oct||tut is arccos(sqrt[3/8]) = 52.238756 degrees
  the hip-6-tut dihedral angle of tut||toe is arccos(-sqrt[3/8]) = 127.761244 degrees
  the tricu-3-tut dihedral angle of tut||toe is arccos(-1/4) = 104.477512 degrees
  thus the sum at the triangle indeed is less than 180 degrees,
  but the sum at the hexagon again exceeds 180 degrees; especially they do not sum to 180 degrees exactly, as was needed for those etcues ...

Seems that in those days I mixed up the combinations in the latter one, as those angles then indeed would sum up to 180 degrees.
Btw., those 2 cases are closely related: the latter is the Stott Expansion of the former wrt. the central node positions. I.e. both will have exactly the same angles between corresponding cells.

--- rk

[student91]

According to my school-project, (bit of the topic of this topic here) when you take o3x3o||x3x3o, and put a xxx3oxo&#x on the o3x3.||x3x3. the. 3x3o||.3x3o will blend with the xxx3...&#x to form a gyrobifastigium. This Johnson solid is special, in that it is not a EKF or diminishing of any uniform polyhedron.
I am not sure whether your list is complete, I should look a bit further into my school-project for that.

[Klitzing]

Wow, that's a great blend of segmentochora, which indeed happens to induce a subdimensional blend of lacing cells too.
Even so your figure is not axial, in that respect it truely matches mines.
And it truely is CRF with dihedrals ranging between 52.2 degrees and 156.7 degrees.
Moreover one rare case incorporating gybef.

Well done!
--- rk

[Klitzing]

Today just found one more axial bistratic stack of segmentochora, which happens to have co-realmic lacing cells, which therefore can be blended in turn into some bistratic Johnsonian solid: here it happens that the squippies (J1) of the upper segment become co-realmic with the trips of the lower one, thus blending into autips (J49)!

• oxx3xox5oxo&#xt - cells are: 1 id + 20 oct + 24 pap + 20 tricu (J3) + 30 autip (J49) + 1 ti

--- rk

Edit:
seems that I've got the dihedral angle of trip-{4}-srid in srid||ti wrong in those days. In fact it ought rather be arccos[-(sqrt(5)-1)/sqrt(12)] = 110.905157 degrees, as can be calculated directly from the height of that segmentochoron and the height of the digonal cupola (trip). Accordingly the angles across that medial srid layer in that bistratic stack all would add to values below 180 degrees. That is, it will indeed be CRF, but autip does not occur here, rather it is a mere adjoin of a squippy and a trip, each.

--- rk

[Klitzing]

... and then the tristratic intercombination of the latter 2, for sure:

• xoxx3oxox5ooxo&#xt - cells are: 1 ike + 40 oct + 12 pap + 12 gyepip (J11) + 20 tricu (J3) + 30 autip (J49) + 1 ti

--- rk

Edit: cf. former post ...

[wendy]

In case anyone is curious about what is going on (including me), we will look at Richard's last example.

xoxx3oxox5ooxo&#xt

Code: Select all

      3     5            3     5     2
    x    o    o    I    x o   o o   x o
    o    x    o   ID    o x   x o   o o
    x    o    x  rID    x o   o x   x x
    x    x    o   tI    x x   x o   x o

We begin by writing each of the symbols in columns, so xoxx is the first column, etc. This gives us four figures with the same symmetry. The &xt tells us that it's a lace tower, made from these as sections, and a unit-edge lacing or thread, running from the vertex of one layer to the vertex of the next. The particular notation only shows consecutive layers, and there is no hint that an edge could run from the first to the third layers, for example. But in effect, this is little different to sections of polytopes down given axies, where in the x3o3o5o `ex`, the exposed pentagons in various sections are burried under pyramids where the apex is a point on an edge that starts above the section, and continues below it.

We read across the rows to find out what they are, inserting a 3 and 5 between these, so x3o5o. This is I (icosahedron) in John Conway's notation, or ike in Jonathan Bower's notation.

The bits to the right represent the three symmetries of the icosahedron, and we look for polyhedra whose top and bottom are various kinds of triangles, pentagons, and rectangles.

The selection of x's and o's here represent the symbols on either side of the 3, 5 or the ends, so eg a3c5e gives a c in the 3 column, c e in the 5 column, and a e in the 2 column. The letters represent kinds of edges that the faces share in these section.

We work down the column, by noting that xo and ox are the same polygon in reciprocal positions, and that xx is a polygon which has the edges of both the original and dual polygon, so where xo is an up-pointing triangle or a N-S line, ox is a down-triangle, or E-W line and xx is a hexagon or rectangle. There are polyhedra formed between the layers, so if one has a N-S line xo on top of an EW line, one has opposite edges of a tetrahedron. Likewise an xo on top of an ox of triangles gives opposite faces of an octahedron, as a 'triangular antiprism'.

Working down a column gives then a string of polyhedra like an orange-quart or a gore on a globe. One has a stack of figures that we shall fold from the top to bottom, like people curve flat strips of paper (gores) to make a globe.

We then get a wrap of 20 polyhedra in the '3' column, being octahedron, octahedron, triangula cupola, 12 in the pentagonal section (pentagonal pyramid, p. antiprism, p.antiprism), and 2 in the '2' section, (square pyramid, digonal cupola = triangular prism, square first). The top (icosahedron) and bottom (truncated icosahedron) survive.

The next trick is that pairs of polyhedra might give a margin angle (dichoral angle) of a half-circle, and the two bits joined. In the pentagonal section, the first two join to give a J11 (johnson-polyhedron #11). J3 is the triangular cupola or tricu in Bower's notation. The two in the digonal column merge to give a single figure J49, autip.

The notation is elegantly brief, but the casual reader could compare what I have written against Richard's remark, to appreciate the subtitlies of what is happening here.

[Klitzing]

you worked it out correctly, Wendy.

The thing is, that 2 consecutive vertex layers define mere - i.e. already well-known - segmentochora. There too your "gores" can be deduced. But as these are segmentochora, these in fact are quite ready for access.

When it comes to stacking next, 2 stacked lacing cells usually have different slopes, and thus the facets of the now becoming pseudo cell, which gets blended out by that stacking adjoin, still will survive. - But occasionally, it happens that 2 sequential lacing cells (one in either segment) will have exactly the same slope. Then not only the 2 segments get blended into a lace tower, but also the joining lateral cells get blended into a larger lacing cell, which reaches through more than just one segment.

This is, how the J11 (gyepip) and J49 (autip) come in:
ox5oo&#x (peppy) + xo5ox&#x (pap) = oxo5oox&#xt (gyepip)
ox2ox&#x (sqippy) + xx2xo&#x (trip) = oxx2oxo&#xt (autip)

The main issue of this thread thus is, looking for "seemingly mere" stacks, which happen to produce corealmic and thus to be joined lateral cells. I.e. which thus happen to be not just a mere stack!

--- rk

[wendy]

You can trace out if there are any further ones by doing an incidence-room calculation. Should draw a piccie up tomorrow for it.

[wendy]

For what it is worth, if one is to trying to find the faces and other surtopes of a lace tower, the key is to look at the lacing edges.

Something like Richard's example above, of xoxx3oxox5ooxo&#xt only have lacing edges between the layers, ie A-B, B-C, C-D. This means that it is in effect a stack of lace prisms, where the co-spacial surtopes merge.

The lace prism given as xof3ooo5oxo&#xt has the usual lace edges AB and BC, as well as AC. It is this third lacing edge that generates the new faces. (This is a section of ex {3,3,5})

Code: Select all

                      -2-    -3-      -5-
      x3o5o A
               AB   xo2ox   xo3oo   oo5ox
      o3o5x B
               BC   of2xo   of3oo   oo5xo
      f3o5o C
               ABC                  AC       xf



In this table, we see the three vertex layers A, B, C. The lacing is vertical, and consists of edges running from one layer to another. Where there is only one lacing-edge, the section has two dimensions of symmetry (essentially a progression from a polygon to a polygon, where digons and points are polygons). The progression on the -2- room is the xo2ox&#xt, a tetrahedron edge first.

If one were dealing purely with a stack of lace prisms with one lacing edge, then the lines as far as ABC suffice.

In ABC, there is an extra edge corresponding to the lace-prism of A to C. This intersects with AB and BC in that C is exposed. Since this is a kind of 'product' or progression where ABC is a triangle, and the stuff to the right of it is orthogonal to it, then we should look it it.

The general progression consists of a "lace city" or altitude, and different vertices are given polytope values. The dimension of the space is then that of the product of the lace-city and the across-symetry. When the lace-city is a simple edge like AB, or BC, the dimension of it is 1, and the face cross-section is 2d.

When the lace-city has 2 dimensions, such as ABC, the across-dimensions form 1d, that is, instead of point || triangle, we have oxo&#t. If AB and BC is supposed to be a stack of lace prisms, then the ones including ABC are things glued onto faces of AB and BC, so that some old faces disappear and new ones appear.

AC has full pentagonal symmetry, since the symmetry is .3o5o in both cases. This means that we are in effect removing the faces formed in the regular stack, (ie the two pentagonal pyramids), and placing five tetrahedra, where A,B,C are the three named points in oxo&#xt (in that order), and the figure is then a line perpendicular to the altitude, and ABC are two triangles attached to this, and joining at C. The two removed faces have pentagonal bases x5o = BBBBB, and the triangles are with vertices ABB and BBC.

[Klitzing]

Yes, Wendy, this is an essential feature, when considering lace towers, that quite often we not only have cells aligning in directions of across-symmetry directions (i.e. o2o, o3o, o5o), but well can have further cells too. These then mostly can be described as cycles or towers in edge directions. Well-known here are the (degenerate) towers ox&#x (triangle) and xx&#x (square), but also things like ofx&#xt (pentagon), xux&#xt (hexagon), xwwx&#xt (octagon) or xFVFx&#xt (decagon, when F=f+x and V=2f) do occur. But in general it is not only that edges or faces fall into such directions, but cells could be asked there as well. Then often lace rings proof useful. That is, things like ooxx&#xr (trigonal prism), oxo&#xr (tetrahedron), xxx&#xr (trigonal prism in a different orientation), xxxx&#xr (cube), xxxxx&#xr (pentagonal prism), or even things like oxofoxo&#xr (mibdi) could turn up.

The reading for lace rings here is quite similar to that of a lace cities: the individual node qualifiers occur in circular order and define true or pseudo edges perpendicular to that plane of the given length each. The final part then is "&#xr", meaning that we have additionally ("&...") lacings (".#..") of size x ("..x."), where the stacking is not a linear tower ("...t") but rather a circle or ring ("r").

Code: Select all

o   x
      = trip = ooxx&#xr
o   x


Beside the concepts of lace prisms ("&#x"), lace towers ("&#xt"), lace rings ("&#xr"), and lace cities (no inline symolization), Wendy uses also the concept of lace simplices. In the latter any 2 "levels" would be connected, just as in a simplex. A lace simplex with just 2 levels then is nothing but a lace prism. Therefore she uses for lace simplices again the same extension "&#x"! Note that a simplex with 3 levels clearly is a triangle. Accordingly we alternatively could write here oxo&#xr = oxo&#x as well as xxx&#xr = xxx&#x.

Code: Select all

o   
   x  = tet = oox&#x
o   


--- rk

PS: OTOH all these extended symbols (and thus your whole comment) so far does not add much to the main quest of this thread:
To decide whether 2 adjacent lacing cells become co-spacial (Dinogeorge once coined "corealmic" for that purpose) or not. ...
Neither does it tell, when having some sub-symbol ...oxo5ooo...&#xt somewhere in the lace tower, which resolution would be needed for the convex bounding (as in CRF researches): whether to pick the 2 attached pentagonal pyramids (as per layerwise consideration: ox.5oo.&#x + .xo5.oo&#x) or to pick the rosette of 5 tetrahedra (as per nodewise consideration: ...oxo...&#x).

[wendy]

The method to find if two elements in a stack, is corealmic (&c), is to find the length of an AC chord in euclidean geometry, and then see if that as lacing gives the same height as the figure.

For example, the diagram i was mentioning before, the faces being joined are two pentagonal prisms. The D2 of a pentagon is 2.8944, the height2 is then (4-2.8944)/4. From apex to apex this height gives 1.1055, but the lacing is 1, so these faces are not co-realmic. Instead, they need to be bent at the B plane to make them fit the lacing of 1.

In xoxx3oxox5ooxo&#xt, the co-realmic nature of the pentagonal symmetry in ABC can be demonstrated, because the figure oxo5oxo is a singly diminished icosahedron, and showing that the lacing of f gives the same height as the AB+BC sections, is sufficient proof that this face is corealmic. Likewise in the rhomic axis (2) we get BCD gives oxx2oxo = point || square || line. The length of the height is (q+h)/2, the drift at the bottom is 1/2, so the lacing here is (5+2qh)+1 / 4 = (3+qh)/2. Were this used as a lacing, from B to D, we would see it is the same as BC+CD, which is sufficient proof that these faces are corealmic.

[Klitzing]

Yep, your argument for the straight stack makes sense.
Thus we just need one for convexity vs. concavity ...
--- rk

[wendy]

Convexity is something which I have been playing around with, using by little zoo of proof lace-towers. It's a little subtler.

[wendy]

Convexity has been solved.

Each of the stack layers like A, B, C represent wythoff polytopes, the faces of which are normal to the vectors v=(1,0,0,0), v2=(0,1,0,0) &c. Thus the normals to these vectors would at some point contain faces of layer A, of B, of C &c. What we plan is to produce a table, A1, A2, A3, ... then B1, B2, B3, ...&c. From this, for the symmetry at 1, we make a tower A1, B1, C1, ... This tower is a scaled copy of the 'gore' profile down the '1' symmetry, and even un-normalised, will correctly show convexity / corealm-ness.

This works, because if P is a point on the face p, and P' is the normal to the face, then P' · P is constant. Since a vertex is a suitable P, on every face, then P1 · V, P2·V, will give the dot-product constant of the several planes through V. A line from A to C will give a greater or lesser value for P·A to P·C averaged at B. It is greater, equal or lesser than P·B as the figure is convex, corealmic, or concaved at B.

We then imagine that A, B, C lie at the ends of an arms of a letter E, where the spacings between the bars are given by the drift table spreadsheet, and the lengths of the arms are given by the dot-product for each gore.

If S is the stott matrix to o---o-5-o, and v is a vector, then ̇S·V is the resulting form needed.

Code: Select all


      3   5
   3-f  2   f
    2   4   2f
    f   2f  3
   
    x 3 x 5 x           (5) (2) (3)
    0   0   0     2f  -  0   0   0
             
    1   0   0     1+f - 3-f  2   f    o----x 2
                                      |     \
    0   0   1      f  -  f   2f  3    o------x 2f
                                      |      |
    f   0   0      1  - 2+f  2f f+1   o------x 2f
             
    0   1   0      0  -  2   4   2f


This is the code for the sections of x3o3o5o, on the icosahedral axis. The matrix at the top represents the stott matrix, in the form I use. This is proportional to the spreadsheet by a factor of 2/(5-3f). This does not matter, since we are abscribing numbers to the different planes.

The table below it shows the first five sections of ex x3o3o5o, given as a lace-tower oxofo3oooox5ooxoo&xt

The next column represents the height coordinate, taken here for a normalised edge of 2.

The next three columns is the vector on each row, multiplied by the matrix in the first table. These represent the gores of the three symmetries (5), (2), (3).

The final column represents the E for the middle three sections of the (2) gore. It does not give the faces, one has to derive these from the first column. But the slices represent from A to E, o2o || x2o (triangle), x2o || o2x (TETRAHEDRA), o2x || f2o (internal), and f2o || o2o (triangle).

[Klitzing]

I see.
You derive kind a comb of the layers for either specific direction.
And the element happens to be internal whenever a tooth of the comb fails to reach its convex hull.

Code: Select all

        (2)

o2o  A   0   x
             | \
x2o  B   2   o---x
             |    \
o2x  C   2f  o-----x
             |     |
f2o  D   2f  o-----x   this f-line will be internal
             |      \
o2o  E   4   o-------x


(columns here representing: element of the considered direction (2), layer character, your derived value, pic of comb with piecewise connection of the teeth)

--- rk

[wendy]

In your picture, the points at B,D,E are co-realmic, giving rise to xfo2ooo&#xt. Since we know the ooo forces the symmetry into the x-h space, the points are actually coplanar. But this test shows they are co-realmic. Layer C represents a line perpendicular to this pentagon, here o2x, and taken with the pentagon in BDE, forms a cycle of five tetrahedra around the edge at C.

Of course, you can treat each comb separately, and unless there is a desire to get the proper margin (dichoral) angles (which come straight off the graph), the colinear and order relations are independent of sheer or scaling (ie x -> ax, y -> by does not affect colinearity of the points).

[Klitzing]

Kind of related to this are the 4 already known CRF polychora of the kind qo3aa3bb4ox&#zx - where a and b independently could be chosen from o and x.

• In fact, qo3oo3oo4ox&#zx is nothing but ico (x3o4o3o) and here is considered as a tes (o3o3o4x) with 8 augmenting cubpies (oo3oo4ox&#x). At each of the squares of tes the 2 adjoining squippies (ox4oo&#x = J1) are corealmic, thereby combining into further octs (oxo4ooo&#xt).
• Then qo3oo3xx4ox&#zx is known as pocsric, a partially Stott contracted version of sric (x3o4x3o). It well could be considered here as a tat (o3o3x4x) with 8 augmenting coatics (oo3xx4ox&#x). At each of the octagons of tat the 2 adjoining squacues (ox4xx&#x) are corealmic, thereby combining into squobcues (oxo4xxx&#xt = J28).
• Next qo3xx3oo4ox&#zx is nothing but spic (x3o4o3x) and here is considered as a srit (o3x3o4x) with 8 augmenting octasircoes (xx3oo4ox&#x). At each square of srit, which is in cubical position, the 2 adjoining squippies (ox4oo&#x = J1) are corealmic, thereby combining into further octs (oxo4ooo&#xt).
• Finally qo3xx3xx4ox&#zx is known to be poc prico, a partially Stott contracted version of prico (x3o4x3x). It well could be considered here as a grit (o3x3x4x) with 8 augmenting toagircoes (xx3xx4ox&#x). At each of the octagons of grit the 2 adjoining squacues (ox4xx&#x) are corealmic, thereby combining into squobcues (oxo4xxx&#xt = J28).

That is, even so these CRFs are not axial ones, and thus slightly overshoot the topic of this thread, here too we have augmentations, which happen to use corealmic lacing cells, which thus can be adjoined in turn in the sense of an external blend. Here we either generate further octs by adjoining corealmic squippies or we generate squobcues by adjoining corealmic squacues.

---rk

[wendy]

This is stott's expansion, such as we get with s3s4o3o => s3s4o3x .

But well done!

[Klitzing]

Just stumbled upon oxux3xxoo3oooo&#xt (cf. that post).
That one is tip = x3x3o3o aligned axially like tut || u-tet || tet, and then being mono-augmented by an oct || tut segmentochoral cap.

Its incidence matrix then is:

Code: Select all

oxux3xxoo3oooo&#xt

o...3o...3o...     | 6  * * * |  4  2 0  0  0 0 0 | 2 2 1  4 0 0 0  0 0 | 1 2 2 0 0 0
.o..3.o..3.o..     | * 12 * * |  0  1 1  2  1 0 0 | 0 0 1  2 2 1 1  2 0 | 0 2 1 2 1 0
..o.3..o.3..o.     | *  * 4 * |  0  0 0  0  3 1 0 | 0 0 0  0 0 0 3  3 0 | 0 0 0 3 1 0
...o3...o3...o     | *  * * 4 |  0  0 0  0  0 1 3 | 0 0 0  0 0 0 3  0 3 | 0 0 0 3 0 1
-------------------+----------+-------------------+---------------------+------------
.... x... ....     | 2  0 0 0 | 12  * *  *  * * * | 1 1 0  1 0 0 0  0 0 | 1 1 1 0 0 0
oo..3oo..3oo..&#x  | 1  1 0 0 |  * 12 *  *  * * * | 0 0 1  2 0 0 0  0 0 | 0 2 1 0 0 0
.x.. .... ....     | 0  2 0 0 |  *  * 6  *  * * * | 0 0 1  0 2 0 1  0 0 | 0 2 0 2 0 0
.... .x.. ....     | 0  2 0 0 |  *  * * 12  * * * | 0 0 0  1 1 1 0  1 0 | 0 1 1 1 1 0
.oo.3.oo.3.oo.&#x  | 0  1 1 0 |  *  * *  * 12 * * | 0 0 0  0 0 0 1  2 0 | 0 0 0 2 1 0
..oo3..oo3..oo&#x  | 0  0 1 1 |  *  * *  *  * 4 * | 0 0 0  0 0 0 3  0 0 | 0 0 0 3 0 0
...x .... ....     | 0  0 0 2 |  *  * *  *  * * 6 | 0 0 0  0 0 0 1  0 2 | 0 0 0 2 0 1
-------------------+----------+-------------------+---------------------+------------
o...3x... ....     | 3  0 0 0 |  3  0 0  0  0 0 0 | 4 * *  * * * *  * * | 1 1 0 0 0 0
.... x...3o...     | 3  0 0 0 |  3  0 0  0  0 0 0 | * 4 *  * * * *  * * | 1 0 1 0 0 0
ox.. .... ....&#x  | 1  2 0 0 |  0  2 1  0  0 0 0 | * * 6  * * * *  * * | 0 2 0 0 0 0
.... xx.. ....&#x  | 2  2 0 0 |  1  2 0  1  0 0 0 | * * * 12 * * *  * * | 0 1 1 0 0 0
.x..3.x.. ....     | 0  6 0 0 |  0  0 3  3  0 0 0 | * * *  * 4 * *  * * | 0 1 0 1 0 0
.... .x..3.o..     | 0  3 0 0 |  0  0 0  3  0 0 0 | * * *  * * 4 *  * * | 0 0 1 0 1 0
.xux .... ....&#xt | 0  2 2 2 |  0  0 1  0  2 2 1 | * * *  * * * 6  * * | 0 0 0 2 0 0
.... .xo. ....&#x  | 0  2 1 0 |  0  0 0  1  2 0 0 | * * *  * * * * 12 * | 0 0 0 1 1 0
...x3...o ....     | 0  0 0 3 |  0  0 0  0  0 0 3 | * * *  * * * *  * 4 | 0 0 0 1 0 1
-------------------+----------+-------------------+---------------------+------------
o...3x...3o...     | 6  0 0 0 | 12  0 0  0  0 0 0 | 4 4 0  0 0 0 0  0 0 | 1 * * * * * oct
ox..3xx.. ....&#x  | 3  6 0 0 |  3  6 3  3  0 0 0 | 1 0 3  3 1 0 0  0 0 | * 4 * * * * tricu
.... xx..3oo..&#x  | 3  3 0 0 |  3  3 0  3  0 0 0 | 0 1 0  3 0 1 0  0 0 | * * 4 * * * trip
.xux3.xoo ....&#xt | 0  6 3 3 |  0  0 3  3  6 3 3 | 0 0 0  0 1 0 3  3 1 | * * * 4 * * tut
.... .xo.3.oo.&#x  | 0  3 1 0 |  0  0 0  3  3 0 0 | 0 0 0  0 0 1 0  3 0 | * * * * 4 * tet
...x3...o3...o     | 0  0 0 4 |  0  0 0  0  0 0 6 | 0 0 0  0 0 0 0  0 4 | * * * * * 1 tet


--- rk

[Klitzing]

I think the once by myself being found segmentochoron cube || ike also was included into Great Stella software. And therein the dihedral angles could be obtained. – Is that correct? (I don't have it myself.)


I just reconsidered that kind of outstanding segmentochoron today, and manually calculated some of its dihedral angles. I got:

• dihedral at {3} between ike and tet: arccos[-sqrt(7+3 sqrt(5))/4] = 157.761244°
• dihedral at {4} between cube and trip: arccos[-sqrt(2/3)] = 144.735610°

Could someone please check these values? (And at best provide the other ones too?)


At least, if these 2 values would be correct, then this would provide further insight onto augmentations of that fellow:

• One might want to augment the cubical base by a corresponding pyramid. As the circumradius of cube || ike equals 1 (in edge units) just as the circumradius of that to be attached pyramid, it would follow that this stack (or tower) pt || cube || ike would have a common(!) circumradius. – But the base dihedral of that to be attached pyramid between cube and squippy is 45°. Accordingly that stack would not be convex!
• On the othenr hand one could aim to augment the other, i.e. the icosahedral base with an according pyramid. Here we no longer could have a common circumradius (as would be the general case for such adjoins). – But as the base dihedral of that to be attached pyramid between ike and tet is arccos(sqrt[7+3 sqrt(5)]/4) = 22.238756°, it happens that these further tets happen to become corealmic with the 8 tets of cube || ike! That is, these would combine into tridpies. Therefore this stack no longer is just that, rather it is a true genuinely polychoron, as it now has cells running through all 3 vertex layers! - And that one then would qualify as CRF.

--- rk

Edit: strikethroughs, cf. next message.

[Klitzing]

Sadly found an error in my yesterday calculation (used the wrong form of spherical cosine theorem). Therefore we rather have

• dihedral at {3} between ike and tet: arccos[-sqrt(7-3 sqrt(5))/4] = 97.761244 degrees

And so instead, at the augmentation of the icosahedral base, those dihedrals at the adjoined tets are no longer corealmic, they rather add to 120 degrees. – Thus nothing special here.

And wrt. the other mentioned angle I went wrong as well. (I used only the height above the circumcenter instead of the total height between the bases.) Hmmm, well. It better ought read

• dihedral at {4} between cube and trip: arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157 degrees

And therefore the pyramidal augmentation at the cube base not only is orbiform, but also convex after all. That is, the tower   pt || cube || ike   happens to be an orbiform CRF!

Should have recalculated all my values independantly. Sorry.
None the less, any volunteer to calculate all the (other) dihedrals of cube || ike ?

--- rk

[student91]

Done that already of all segmentochora, cf the attachment. I found it only to be possible to add pyramids on both sides, giving o4o3o||o4s3s||x4o3o||o4o3o etc.

[Klitzing]

Could you explain your cryptix related to the dihedrals in your pic? I cannot relate them all to according faces.
How does that value 122.238756 comes up? I cannot derive an according algebraic term for its cosine.
To my view cube||ike has only 6 face types. Where come your 7 values from?
And cube||ike is K-4.21 ...
--- rk

[student91]

Oh you're right, I have no idea what I did there.

[Klitzing]

Got an interesting seed for some new potential CRFs.

Take a simple cube. Then attach 2n-prisms in pyrohedral symmetry onto the 6 squares, i.e. each neighbouring pair is mutually orthogonal. Further attach an n-cupola onto each 2n-gon in that orientation, so that one of its lacing squares can attach to the neighbouring prism. Then the 2 neighbouring lacing triangles of these cupolae allow for an attached tetrahedron, which thereby become vertex-opposing to the cube's vertices.

The case of n=2 here already is well-known. It is nothing but the segmentochoron cube||sirco. There the lateral prisms become further cubes and the cupolae become just triangular prisms. The above partial description then is all of that polychoron, except of the bottom sirco. That segmentochoron, by the way, is nothing but a cap of sidpith = x3o3o4x, so it even could be continued beyond that short closure with just 1 sirco.

The case of n=4 also is special and already solved. In that case the overall curvature becomes flat. Accordingly the octagonal prisms and the attaching 2 cupolae unite into sircoes each. And the according honeycomb then is just ratoh = x3o3o *b4x.

But the cases of n=3 and n=5 both would belong to spherical curvature and, up to my knowledge, still ask for continuation of that partial seed complex. If either one of those could be closed somehow, it would be a fascinating new CRF! - Any ideas for continuation?

--- rk

[quickfur]

Hey Klitzing,

I finally got round to reading the above post of yours, and I must say, it's a very, very interesting idea!

And what's even more interesting is when I began constructing a model of the n=3 case in my polytope viewer. Starting with the cube at w=0, and using my usual edge length=2, I discovered that the equatorial vertices of the hexagonal prisms lies on w=1/phi, where phi = the golden ratio (1+√5)/2. The appearance of phi is linked with the pyritohedral symmetry of the construction, of course, but it turns out to be even more than that. The far vertices of the hexagonal prisms are, of course, at w=2/phi. When I computed the remaining vertices of the triangular cupolae, i.e., the last vertex of the top triangular face of the cupolae, it turns out to also lie on w=2/phi. Now here's the most interesting part: the distance between the tip of the cupola and the tip of the adjacent hex prism that isn't sharing a hexagonal face with it, is exactly phi*edge_length. And taken together, all of these vertices that lie on w=2/phi form a subset of ... guess what? the vertices of a x5o3x !!!

Unfortunately, completing the x5o3x does not yield a CRF, because the w=1/phi vertices are too close to it, and produce cells of the shape edge || pentagon, which is non-CRF.

But it doesn't just stop there... if you look at the vertices of the starting cube, after attaching the hex prisms and cupolae you'll get tetrahedra touching them. Looking at the opposite faces of the tetrahedra and the faces sharing an edge with it, I see the configuration is 3 squares alternating with phi-edged isosceles triangles, i.e., fragments of another x5o3x that intersects with the x5o3x that lies on the hyperplane w=2/phi. So what this means is that your little construction here is actually nothing other than erecting a "cube-topped 4D cupola" over a subset of the surface of one of the non-convex 4D uniforms from the 120-cell family! Specifically, it's one where the x5o3x's intersect with each other in cross-sections that look like (non-CRF, of course) hexagonal cupola with 3 alternating phi-edged hexagons. I don't know the non-convex members of the 120-cell family that well, but possibly you can identify which one I'm talking about.

This isn't the end of the story, of course. The fact that we're dealing with a uniform of the 120-cell, albeit a non-convex one, gives me hope that this construction can be completed in a CRF way. It could be possible that what we have is just a fragment of some kind of augmentation of this non-convex uniform, and perhaps this augmentation may even be CRF!

[Klitzing]

yes, Quickfur, I too - right after my above post - calculated several vertex coordinates and thus derived according distances.
I, just as you, was surprised too, to find lots of well-known distances. But finally I abandond this little project cause of that asked for v=1/f distance, you found as well, which couldn't be omitted.
But you might be right indeed that it probabbly could be continued as an interesting nCRF.
Did you make any further progress on that in the last days?

In those days I calculated those distances via coordinates, and these in turn all by hand on paper. Not the fastest way to do, as you now. And quite often error prone. So I had to recalculate them several times. But, as there are already some months in between, I now even don't know whether I saved these calculations at all.

So could your program perhaps put out the so far constructed vertex layers - at least as if it would be convex (i.e. its hull)? Possibly also in lace tower description? That would help a lot in order to get in again!

--- rk

[quickfur]

Actually, I also primarily work with coordinates. The lace tower constructions in my past posts are what I use to guide me in constructing the right coordinates. I was planning to write a program that understands lace towers so that I don't have to deal with them manually, but I haven't gotten around to it yet. I do have a convex hull algorithm in place, though, but what I have so far is only the convex hull of your initial starting seed, and also an alternate model where I completed the x5o3x, with the 1/f edges that can't be removed. If you're interested I can post renders of these models... not sure if they are of any help in continuing the construction, though.

I haven't worked on this after posting my previous comment, unfortunately. I did consider several different possibilities to continue, to try to "cover over" the regions that would require 1/f edges, but haven't actually computed them, so I don't know if they will work or not.

A different approach I thought about, was to Stott-expand the cube into a x4o3x, with some adaptations of the cupola cells, the idea being that in a Stott expansion we may be able to avoid the 1/f edges completely. Might be worth exploring.

[quickfur]

Actually, no harm posting the image I have so far, maybe it will lead to some new ideas:



P.S. This is the model with the x5o3x completed, so you can see some non-equilateral triangles and non-CRF cells.

[quickfur]

Haha, looking at the image again, I decided to use my polytope viewer to calculate the angle between the square face of the hex prism and the triangular top of the adjacent cupola. Turns out to be: 110.9051574479 degrees. Is there a CRF 3D cell that contains this angle between a square and a triangle?