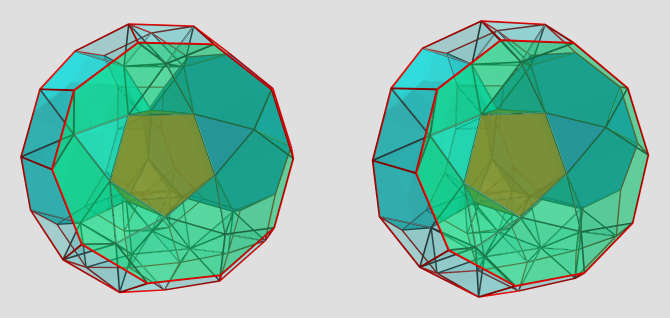
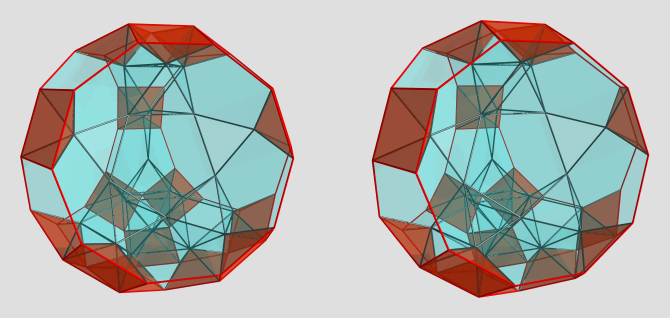
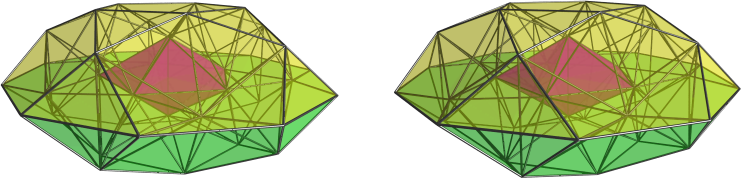
I'd highly recommend getting familiar with the Dynkin symbols, since they are extremely useful not only in notating shapes precisely, they also help a great deal in computations of coordinates. They are especially handy in dealing with CRFs, because the regular polygons in CRFs have well-known symbols and can be manipulated easily that way.
Take for example the octahedral teddy, which can be expressed as the symbol ooo4oox3xfo&#xt. This is just a compact notation for the following lace tower:
- Code: Select all
o4o3x
o4o3f
o4x3o
The "ooo" in "ooo4oox3xfo..." appears as the first column of the tower; the "oox" appears as the second column, and the "xfo" appears as the 3rd column. So basically the linear symbol is just a compression of this lace tower (since all elements are of the form .4.3. so we just write the 4 and 3 once, and transpose the columns into rows between them. The "&#xt" just means "the vertex layers are to be laced with unit edges". That is, the exact distance between, say, o4o3x and o4xo3f is not specified, but can be computed using basic trigonometry, since we know what the final edge length (i.e. the hypotenuse) must be.
Now let's look at each individual layer of this tower. While the "standard" interpretation of the Dynkin symbol involves confusing (to me!) explanations of mirrors and angles and what-not, I personally find it easiest to think of it as a coordinate system (IIRC this was Wendy's idea) along the edges of a regular polytope.
Let's take o4o3x to start. Whenever you see 'o' in the symbol, it means the corresponding coordinate in the coordinate system is zero; whenever you see 'x' the corresponding coordinate is 1. But what are these coordinates referring to? I find it most helpful to think in terms of folding polygons (resp. polytopes) around a ridge (i.e., (n-2)-dimensional element). The beautiful thing about Dynkin symbols is that substrings of the symbol exactly describe sub-dimensional elements of the polytope. So in o4o3x, for example, the substring o3x describes a triangle. Why? Because the 3 means that 'x', which is a unit edge (remember, 'x' means '1'), is folded around a 3-fold axis. What does that make? A triangle, of course! The 'o' means that the 'x' is folded around the 3-fold axis without any intervening edges. If you were to write x3x, for example, that would mean that it's a hexagon, because you're folding 'x' around a 3-fold axis, with the other 'x' indicating a unit displacement around the joint. So the 'x' describes every other edge of the hexagon, and the other 'x' describes the other 3 edges. Notice that the symbol x3x is palindromic, which means you can read it backwards and it still means the same thing, which makes sense 'cos it doesn't matter which set of 3 edges you start with the make the hexagon. You could start with folding edges 1, 3, 5, say, with a unit distance between them (i.e., interpret the first 'x' as the starting shape and the other 'x' as displacement), or fold edges 2, 4, 6 with unit distance between them (i.e., interpret the second 'x' as the starting shape and the first 'x' as displacement), and the result would be the same. The Dynkin symbol neatly captures this equivalence by being equivalent to its mirror image.
OK, so now we've determined that o3x is a triangle. What about x3o? Remember that 'o' means 'zero', so it's just a single point. We're folding a single point around a 3-fold axis (as indicated by the '3'), with a displacement of 1 (as indicated by the 'x'). So again, we have a triangle. You could equivalently interpret this by reading from the other direction, i.e., 'x' means an edge, '3' means fold it around a 3-fold axis, and o means zero displacement. Either interpretation gives you a triangle. However, there's a difference between o3x and x3o: remember that this is a coordinate system, so while (1,0) in the Cartesian coordinate system has the same length as (0,1), it's pointing in a different direction. Similarly, x3o describes a triangle that's pointing in a different direction from o3x. Which direction? Exactly the direction perpendicular to the "displacements" we were dealing with in the x3x example. Or, more generally speaking, in the
dual orientation. So o3x is a triangle, and x3o is the dual triangle. The fact that the Dynkin symbol is not palindromic indicates a distinction between the two. In the case of x3x, we're talking about the hexagon inverted along a 3-fold (not 6-fold) axis; so in the triangular coordinate system .3., the hexagon is in some sense "self-dual". Or, to be more precise, orienting the hexagon in the orientation of the dual triangle does not change it.
OK, enough of boring old 2D shapes. Now let's go back to the original symbol o4o3x. There are various ways of reading this, but let's build upon what we've learned above, that o3x describes a triangle. So we can read this symbol as o4(o3x), that is, fold triangles around a 4-fold axis. What do we get? We get a square pyramid. But it doesn't end there; the Dynkin symbol is transitive across symmetries, so we're talking about something that contains triangles meeting 4 to a vertex. That is, of course, an octahedron. So that's how o4o3x describes an octahedron. Now, we could equivalently read the symbol as (o4o)3x, that is o4o describes points folded around a 4-fold axis (it's still just a point -- it's a kind of degenerate square, you can think of it), and then folding these degenerate squares (i.e. points) in 3D around 3-fold axes. Remember that .4. is a coordinate system for squares, so o4o can be thought of as a point in the middle of a square. So folding o4o around a 3-fold axis is equivalent to folding squares around a 3-fold axis, that is, you get a cube, and then placing points in the middle of each square face. I.e., we get an octahedron, as expected.
(This, of course, suggests that if ithe squares
weren't degenerate, we'd actually get a cube, which is precisely what happens when we write x4o3o. That is, x4o describes a square (fold 4 edges around a 4-fold axis), and x4o3o = (x4o)3o means fold squares around a 3-fold axis, so you get a cube.)
OK, so o4o3x means an octahedron. But what does o4o3f mean??! Well, f is shorthand for the Golden Ratio phi=(1+√5)/2. It means we start not with a unit edge, but with an edge of length phi, and fold it along a 3-fold axis, producing a triangle scaled by phi, and then fold that around a 4-fold axis, that is, an octahedron scaled by phi. So we see that the second layer of vertices in the octahedral teddy is an octahedron scaled by phi.
If we were to connect these two layers together with unit edges, we'd get an octahedron of unit edge length on top, an octahedron of edge length phi on the bottom, and in the middle, the lacing edges, also of unit length, would trace out trapeziums with 3 unit edges and 1 phi edge. If you think about this carefully, you'd realize that these trapeziums are nothing other than incomplete pentagons. So the first two layers of our tower o4o3x || o4o3f describes a partial shape that has incomplete pentagons. These pentagons are completed by the final layer, o4x3o.
What is o4x3o? Note that, while in 2D it didn't matter which way you read the symbols, in 3D and above it does matter which side of the symbol is connected to the rest of it, that is, o4x3o is
not the same as o4o3x. This is because o3x describes a triangle in "normal" orientation, such that folding it around a 4-fold axis would eventually produce an octahedron. x3o, however, describes triangles in the same positions as the o3x triangles, but in dual orientation. So imagine if you were to take an octahedron and spin its faces in-place so that they are now in dual orientation to the original triangles. What you get are 8 triangles that are in the same orientation as a cuboctahedron. And in fact, that's what o4x3o describes: a cuboctahedron. Equivalently, you can read it is (o4x)3o, i.e., o4x is a square in dual orientation to the squares in a cube (a cube is x4o3o, remember), so if you fold dual squares around 3-fold axes, you get a cuboctahedron.
There's another way to look at the Dynkin symbol, and that is by taking a regular polytope of the same symmetry as the basis for interpreting it. For example, let's take the cube as the "standard" shape for symbols of the form a4b3c. Then the first element a refers to the vertices of the cube, the second element b refers to the edges of the cube, and the last element c refers to the faces of the cube. By "refer" I mean draw vectors from the origin (assuming the cube is origin-centered) to the indicated element. For the first element, you have 8 vectors (there are 8 vertices in the cube), that is, <±1,±1,±1>, or apacs<1,1,1>. The second element corresponds to the vectors apacs<0, √2, √2> (why √2 will be explained in a bit), and the 3rd element to the vectors apacs<0, 0, √2>. Given a symbol a4b3c, the resulting polyhedron is the convex hull of a*apacs<1,1,1> + b*apacs<0, √2, √2> + c*apacs<0, 0, √2>. So when you write x4o3o, that means a=1, b=0, c=0, so you get a cube. When you write o4x3o, that means a=0, b=1, c=0, so you get a cuboctahedron (of the same edge length as x4o3o, and that is why we use <0, √2, √2> rather than <0, 1, 1>). If you write x4x3o, for example, your polyhedron would be apacs<1,1,1> + apacs<0, √2, √2>, which is equivalently apacs<1, 1+√2, 1+√2>, which, if you graph it out, is a truncated cube (of the right edge lengths!!). Similarly, o4x3x describes a truncated octahedron, x4o3x describes a (small) rhombicuboctahedron, etc.. So once you know the basis vectors for a particular edge labelling of the Dynkin diagram, the Dynkin symbol basically tells you how to compute its coordinates, in addition to being an intuitive description of how to obtain the shape by folding lower-dimensional elements into higher dimensions(!).
Now coming back to our tower...
The bottom symbol is o4x3o. Note that the orientation of the triangles is in dual orientation to the top symbol o4o3x. So in terms of the partial pentagons produced by the first two layers, the vertices of o4x3o are precisely in the right place to complete the pentagons and close up the shape, as they would if we were to lace the last layer to the 2nd by unit edges, as the suffix &#x indicates.
This isn't all there is to the lace tower, though. Remember what I said about substrings of the Dynkin symbol? That principle can also be applied to lace towers! For example, we can read off the 1st two nodes of our tower, and we'd get o4o || o4o || o4x. That is, a point, another point, then a square. Well, point || point is obviously an edge, so that means that in the position of symmetry described by the first 2 nodes of the symbol, there are edges, not full-dimensioned elements. Then we have point || square, which is obviously a square pyramid. This tells us that there are square pyramids in this position of symmetry. But what is this position of symmetry? Remember the symbol for the cube: x4o3o. The first two positions is (x4o), i.e., where the faces of the cube lie. So that tells us that the square pyramids are found where the faces of a cube, oriented in the same way as the octahedral teddy, would lie. Therefore, there are exactly 6 square pyramids. (See? We can know this just by reading the Dynkin symbol, without even "visualizing" the polychoron!).
Similarly, if we read the last 2 symbols of each layer, we get o3x || o3f || x3o. That is, triangle || phi-scaled triangle || dual triangle. This describes a teddi. And since these last 2 symbols correspond with the faces of an octahedron, this tells us that there are exactly 8 teddies in this polychoron. And so, we learn that the polychoron has 6 square pyramids, 8 teddies, 1 octahedron, and 1 cuboctahedron.

There's still more to this, of course. E.g., you can read the first and last symbols (deleting the middle node, which is equivalent to writing '2', and that lets you read off prism symmetries, i.e., elements that correspond to the edges of the cube). For example, if we delete the middle column, we get o2x || o2f || o2o. The 2 here is actually an abuse of notation, because in the "real" Dynkin diagram there's actually no edge between the two nodes, but it serves as a nice mnemonic for "put two copies of the base shape on parallel (hyper)planes to make a prism". Here, o2x is a unit edge (i.e., a point prism), o2f is a phi-scaled edge, and o2o is a point. This, in fact, describes a pentagon (the o2f is just a short-chord of the pentagon, you see). Since the first node is consistently o, the "prism" here is degenerate; it just flattens into a polygon (the height of the prism is 0). If we had x2x || x2f || x2o instead, we'd have a pentagonal prism, which can be interpreted as square (x2x) || 1*phi rectangle (x2f) || line (x2o).
Just for kicks, let's read off the element types of a 4D uniform polychoron, say o5x3o3x. The first 3 nodes are o5x3o, so that means we have icosidodecahedra (o5(x3o) == dual triangles folded around 5-fold axes (thus attached by their vertices), or equivalently, (o5x)3o == dual pentagons folded around 3-fold axes, attached by their vertices) in the position corresponding to the cells of the 120-cell, so 120 icosidodecahedra. The last 3 nodes are x3o3x, i.e., cuboctahedron (as rhombi-tetrahedron: (x3o)3x = 4 dual triangles folded around 3-fold axes a unit displacement apart, this causes the original tetrahedron edges to expand into squares and 4 more triangles from the dual tetrahedron to appear), in the position corresponding to the cells of the 600-cell, so there are 600 cuboctahedra. Deleting the 2nd node gives us o2o3x, i.e., triangles (triangular prisms of height 0), and deleting the 3rd node gives o5x2x, i.e., pentagonal prisms. So we see that o5x3o3x consists of icosidodecahedra, cuboctahedra, and pentagonal prisms (and triangles, but they are subdimensional).
OK this post has become far longer than I anticipated. I'll shut up now.
 Edit:
Edit: Corrected some silly errors in the o5x3o3x example.
Edit 2: Corrected yet more silly errors.
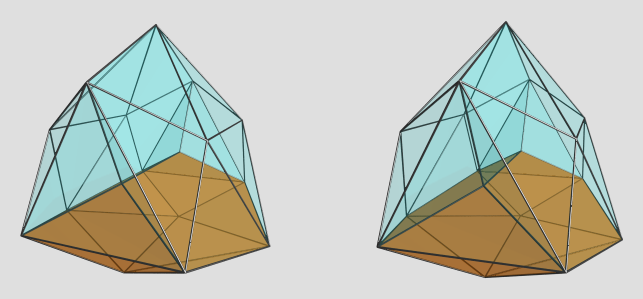

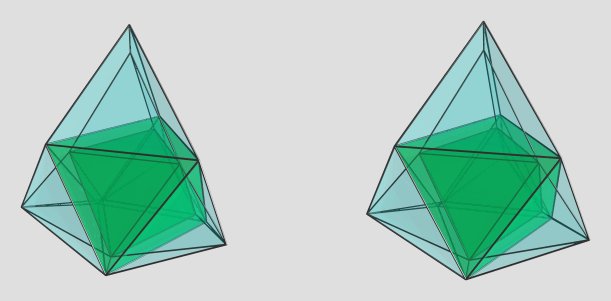
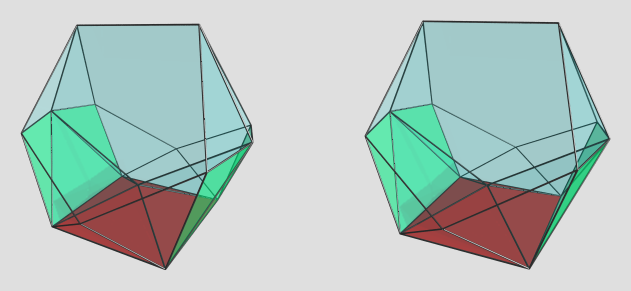


 ). Would something like this be possible? If this lace tower is CRF-able, can there be higher-dimensional analogues? Is there an infinite family of these wedge-like ursatopes? (No idea what to call them... ursawedges?)
). Would something like this be possible? If this lace tower is CRF-able, can there be higher-dimensional analogues? Is there an infinite family of these wedge-like ursatopes? (No idea what to call them... ursawedges?)

![Pleased :]](./images/smilies/pleased.gif) Oh, and Pi Day! It's that too!
Oh, and Pi Day! It's that too!