A different way to expand an ursatope?
102 posts
• Page 1 of 4 • 1, 2, 3, 4
A different way to expand an ursatope?
An idea occurred to me today. We know that teddi, the 3D triangular ursahedron, coincides with the tridiminished icosahedron. In 3D, the square ursahedron and pentagonal ursahedron are non-CRF because of the bottom face, which has non-unit chord lengths. In 4D, we get CRF ursachora from the tetrahedron, octahedron, and icosahedron. Thus far we have discovered a kind of "runcination" of the 4D ursachora, produced by (partial) Stott expansion along the symmetries of the tetrahedron (resp. octahedron, icosahedron), which introduce prisms between the teddi cells.
Now, in 3D, a different kind of Stott expansion of the teddi produces the tridiminished rhombicosidodecahedron (J83), where the pentagons become decagons, and the vertices expand into pentagons, and edges into squares. So the question is, is it possible to perform this kind of (partial) Stott expansion on the 4D ursachora as well? I.e., is it possible to get a CRF by starting with a tetrahedron (resp. octahedron, icosahedron), attach triangular prisms and perhaps some other kind of prisms, such that in the place of teddi cells we have J83 cells instead, with the bottom of the polychoron suitably modified to close things up?
Now, in 3D, a different kind of Stott expansion of the teddi produces the tridiminished rhombicosidodecahedron (J83), where the pentagons become decagons, and the vertices expand into pentagons, and edges into squares. So the question is, is it possible to perform this kind of (partial) Stott expansion on the 4D ursachora as well? I.e., is it possible to get a CRF by starting with a tetrahedron (resp. octahedron, icosahedron), attach triangular prisms and perhaps some other kind of prisms, such that in the place of teddi cells we have J83 cells instead, with the bottom of the polychoron suitably modified to close things up?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Hmm, you might consider srahi = o3x3o5x. That one at least has lots of srids (. x3o5x). These then ought to be diminished by parallel cuts wrt. their pentagons. Thus the question here becomes: what is the sefa (sectioning facet underneath) of these pentagons. And, well, here it comes out to be just the decagonal prism. I.e. the split off fragments then are nothing but the well-known friends, the pentagonal magnabicupolaic ring, aka pepuf (= pentagonal pucofastegium).
Thus, in order to obtain tedrids (= tridiminished rhombicosidodecahedra), you'll just have to diminish srahi at several pentagons. Thereby introducing there their sefas, i.e. these decagonal prisms. And all the remainder could still stay as before.
--- rk
Thus, in order to obtain tedrids (= tridiminished rhombicosidodecahedra), you'll just have to diminish srahi at several pentagons. Thereby introducing there their sefas, i.e. these decagonal prisms. And all the remainder could still stay as before.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Actually, I was thinking more along the lines of, start with a deltahedron like tetrahedron, octahedron, or icosahedron as the "top" cell, then attach triangular prisms to each face, and on the opposite ends of the triangular prisms attach tetrids. I'm not 100% sure what should come between the prisms, touching each edge of the top cell; perhaps more prisms of some kind to interface with the square faces of the tetrids? Then fold the tetrids down and either connect their decagonal faces together, if possible, or insert decagonal prisms if necessary. On the far ends of the tetrids, insert another layer of cells to link to the "bottom" cell, antipodal to the top cell. I'm not 100% sure what this should be, perhaps a rectified version of the top cell?
Is such a construction possible?
Is such a construction possible?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Another way to think about this, is to take an ursachoron, apply (pseudo-)Stott expansion (i.e., move all cells apart from each other radially), then replace the teddies with tetrids, inserting additional cells as needed to fill in any gaps. Can such a process be made to yield a CRF?
For a more specific instance, let's say we start with 4 tetrids, arranged in tetrahedral symmetry, such that the decagonal faces are joined to each other. Can this starting configuration be made CRF by adding more cells to fill in the gaps?
Similarly, suppose we start with the 4 tetrids in tetrahedral configuration, then insert decagonal prisms between them such that they all link up. Can more cells be added to make this shape close up into a CRF?
For a more specific instance, let's say we start with 4 tetrids, arranged in tetrahedral symmetry, such that the decagonal faces are joined to each other. Can this starting configuration be made CRF by adding more cells to fill in the gaps?
Similarly, suppose we start with the 4 tetrids in tetrahedral configuration, then insert decagonal prisms between them such that they all link up. Can more cells be added to make this shape close up into a CRF?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
I think I've found a potential construction that might work. At least, the top part of the polytope topologically closes up (though I haven't verified if it will actually close up as a CRF in Euclidean 4-space). Here's the (partial) construction:
- Start with a cuboctahedron, as a "rhombi-tetrahedron", that is, x3o3x.
- On 4 of the triangular faces, in tetrahedral symmetry, attach 4 tetrids, such that their decagonal faces join to each other.
- On the other 4 triangular faces of the x3o3x, attach teddies, via their *bottom* face (i.e., the triangle that does not share any edges with pentagons, only vertices). The "top" face of the teddies will end up sitting between 3 pentagons of the tetrids, thus outlining a triangular prism that will sit between a subset of square faces of the tetrids.
- Between the x3o3x's and the tetrids, it should be possible to close up the gaps with more triangular prisms. Thus, the x3o3x should end up with its 6 square faces joined to 6 triangular prisms; each of these triangular prisms' remaining two square faces are joined to the tetrids.
I haven't figured out yet what will come below the triangular prisms under the teddies, but at least thus far the construction seems to be CRF-able. My present intuition suggests that some kind of cupola should be involved toward the bottom of the tetrids, perhaps with more teddies, and probably more triangular prisms bridging the antipodal cell. Currently unsure what the antipodal cell will be... perhaps another x3o3x, or maybe x3x3x?
If this construction "works", it might be possible to also construct variants with octahedral symmetry, I think. This would extend the family of ursachora to a bigger set than previously anticipated!!!! (Higher-dimensional equivalents ought to be possible, by using lower-dimensional ursatopes to fill in the roles of the teddies and tetrids.)
- Start with a cuboctahedron, as a "rhombi-tetrahedron", that is, x3o3x.
- On 4 of the triangular faces, in tetrahedral symmetry, attach 4 tetrids, such that their decagonal faces join to each other.
- On the other 4 triangular faces of the x3o3x, attach teddies, via their *bottom* face (i.e., the triangle that does not share any edges with pentagons, only vertices). The "top" face of the teddies will end up sitting between 3 pentagons of the tetrids, thus outlining a triangular prism that will sit between a subset of square faces of the tetrids.
- Between the x3o3x's and the tetrids, it should be possible to close up the gaps with more triangular prisms. Thus, the x3o3x should end up with its 6 square faces joined to 6 triangular prisms; each of these triangular prisms' remaining two square faces are joined to the tetrids.
I haven't figured out yet what will come below the triangular prisms under the teddies, but at least thus far the construction seems to be CRF-able. My present intuition suggests that some kind of cupola should be involved toward the bottom of the tetrids, perhaps with more teddies, and probably more triangular prisms bridging the antipodal cell. Currently unsure what the antipodal cell will be... perhaps another x3o3x, or maybe x3x3x?
If this construction "works", it might be possible to also construct variants with octahedral symmetry, I think. This would extend the family of ursachora to a bigger set than previously anticipated!!!! (Higher-dimensional equivalents ought to be possible, by using lower-dimensional ursatopes to fill in the roles of the teddies and tetrids.)
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Wow, that one looks promising, indeed!
Well, what comes after the trips attached at the farer end of the teddies (J63)?
Obviously there must be teddies again (reversed axial orientation). And at the neighbouring last squares - adjoining to the pairwise connected decagons of the tedrids (J83) - we have to use trips once more. And thus the final keystones at the top of these decagons then ought be mibdies (J62). Therefore our so far shifted open end now only uses partial boundaries of ikes (teddi and mibdi) and srids (tedrid). But only triangles and squares are still open now, pentagons and decagons all have been accomplished already so far.
Anyone likes to come in and push beyond? - E.g. each medial top triangle of the second teddies, together with the 3 neighbouring squares of the trips and the triangles (of the tedrids) inbetween, would either provide place for a further co, or at least a tricu (J3) ...
--- rk
Well, what comes after the trips attached at the farer end of the teddies (J63)?
Obviously there must be teddies again (reversed axial orientation). And at the neighbouring last squares - adjoining to the pairwise connected decagons of the tedrids (J83) - we have to use trips once more. And thus the final keystones at the top of these decagons then ought be mibdies (J62). Therefore our so far shifted open end now only uses partial boundaries of ikes (teddi and mibdi) and srids (tedrid). But only triangles and squares are still open now, pentagons and decagons all have been accomplished already so far.
Anyone likes to come in and push beyond? - E.g. each medial top triangle of the second teddies, together with the 3 neighbouring squares of the trips and the triangles (of the tedrids) inbetween, would either provide place for a further co, or at least a tricu (J3) ...
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
... okay, assuming there further coes, this would require trips (as digonal cupolae) attached to the remaining square faces of the tedrids. - This now leaves us with a single open triangle of each of those 4 further coes (the one at the far end of each co-teddi-trip-teddi-co column), 4*3=12 square faces of these last squeezed in trips. The triangular faces of those would attach to the mibdies, just as the other triangles of those coes do. Therefore those 6 mibdies would have left open just the 2 "opposing" triangles (i.e. the ones, where the connecting edge is parallel and antipodal to the connecting edge of the Pentagons). And each tedrid has left open only its antipodal triangle any longer.
Wrt. the antipodal triangles (and surroundings) of the tedrids it is evident that we can introduce either coes or at least tricues there. In fact the hemisphere then would be adjoined completely to those neighbouring trips and mibdies.
Assuming coes once more, then the further lateral triangles should attach pairwise (if I'm not totally wrong), while the still open triangle each of the former coes here allows for a further trip. The lateral squares then would attach to the so far open squares of these new coes. Therefore we are left now just with one opposing triangle of these last coes (the opposing one to the 4 tedrids) and with the opposing triangles of these 4 now extended co-teddi-trip-teddi-co-trip columns. Thus the final keystone would be just a simple octahedron. - And we are done!
Thus, this new CRF (if I recounted correctly) would have a cell total of
1+4+4 = 9 coes
4+4 = 8 teddies (J63)
4 tedrids (J83)
6+4+3*4+3*4+4 = 38 trips
6 mibdies (J62)
1 oct
--- rk
Wrt. the antipodal triangles (and surroundings) of the tedrids it is evident that we can introduce either coes or at least tricues there. In fact the hemisphere then would be adjoined completely to those neighbouring trips and mibdies.
Assuming coes once more, then the further lateral triangles should attach pairwise (if I'm not totally wrong), while the still open triangle each of the former coes here allows for a further trip. The lateral squares then would attach to the so far open squares of these new coes. Therefore we are left now just with one opposing triangle of these last coes (the opposing one to the 4 tedrids) and with the opposing triangles of these 4 now extended co-teddi-trip-teddi-co-trip columns. Thus the final keystone would be just a simple octahedron. - And we are done!
Thus, this new CRF (if I recounted correctly) would have a cell total of
1+4+4 = 9 coes
4+4 = 8 teddies (J63)
4 tedrids (J83)
6+4+3*4+3*4+4 = 38 trips
6 mibdies (J62)
1 oct
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
I decided to try constructing the full polychoron last night. I'm happy to report that it's a success!!!! Here is the lace tower (there may be mistakes, in several of the layers I obtained the coordinates by "completing the pentagons/decagons" rather than straight from the CD symbol, so I may have gotten the symbols wrong):
I'm 99% sure this is CRF -- my polytope viewer reports that all edge lengths are equal. There's still a slight chance some of the squares are rhombuses, if I screwed up the construction somewhere, but I highly doubt it. Could somebody confirm?
Anyway, let's take some pictures of this baby!! Here's the top view, looking at the x3o3x:

Here, you can see the triangular prisms around the x3o3x interfacing with the upside-down teddies and the tetrids. The tetrids appear quite flat from this viewpoint because they are quite slanted into the 4th direction. You can see the outlines of the 2nd layer of teddies at the corners of the tetrahedroid shape of the projection, around the outer triangular prisms (they are on the far side of the polychoron from this viewpoint).
The most interesting part of this polychoron is the bottom. It turns out that it can be closed with just another layer of vertices beyond the tetrids, as indicated by the lace tower; among the cells that fill in the gaps are metabidiminished icosahedra and more cuboctahedra! Along with triangular cupolae.

The green cells are cuboctahedra linking the bottom cell to the 2nd layer of teddies. Between each pair of cuboctahedra are metadiminished icosahedra, serving as wedges that sit between the gaps between the bottom part of the tetrids, more triangular prisms, and triangular cupolae linking the bottom cell to the bottom triangles of the tetrids.
So far, we haven't had a good view of the tetrids, so let's take a side view next:
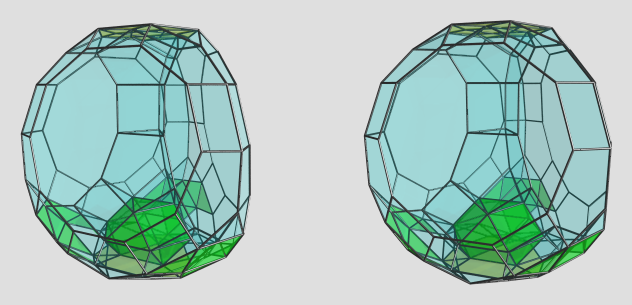
Here, we're looking at how 3 tetrids fold together around a column of teddies and triangular prisms. Below the 2nd layer of teddies we have cuboctahedra linking to the bottom cell.
I'll post the coordinates later.
- Code: Select all
x3o3x (top cuboctahedron)
x3f3o (top half of (upside-down) teddies)
F3x3o (end of teddies)
V3x3o (V=f+f, I think. This is half of the decagons)
F3f3o (not 100% sure about the f, this is 2nd last set of vertices of decagons)
/ \
x3B3o C3o3f (not sure what B and C are, this is last vertices of decagon and 2nd set of teddies)
\ /
f3x3D (2nd last layer of vertices of tetrids, not sure what D is)
o3x3f (last vertices of tetrids)
x3x3o (bottom cell, it turns out to be a truncated tetrahedron!)
I'm 99% sure this is CRF -- my polytope viewer reports that all edge lengths are equal. There's still a slight chance some of the squares are rhombuses, if I screwed up the construction somewhere, but I highly doubt it. Could somebody confirm?
Anyway, let's take some pictures of this baby!! Here's the top view, looking at the x3o3x:

Here, you can see the triangular prisms around the x3o3x interfacing with the upside-down teddies and the tetrids. The tetrids appear quite flat from this viewpoint because they are quite slanted into the 4th direction. You can see the outlines of the 2nd layer of teddies at the corners of the tetrahedroid shape of the projection, around the outer triangular prisms (they are on the far side of the polychoron from this viewpoint).
The most interesting part of this polychoron is the bottom. It turns out that it can be closed with just another layer of vertices beyond the tetrids, as indicated by the lace tower; among the cells that fill in the gaps are metabidiminished icosahedra and more cuboctahedra! Along with triangular cupolae.

The green cells are cuboctahedra linking the bottom cell to the 2nd layer of teddies. Between each pair of cuboctahedra are metadiminished icosahedra, serving as wedges that sit between the gaps between the bottom part of the tetrids, more triangular prisms, and triangular cupolae linking the bottom cell to the bottom triangles of the tetrids.
So far, we haven't had a good view of the tetrids, so let's take a side view next:

Here, we're looking at how 3 tetrids fold together around a column of teddies and triangular prisms. Below the 2nd layer of teddies we have cuboctahedra linking to the bottom cell.
I'll post the coordinates later.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
P.S. The cell counts:
1+4 = 5 x3o3x
6+4+12+12 = 34 triangular prisms
4+4 = 8 J63's (teddies)
4 J83's (tetrids)
6 J62's (mibdies)
4 triangular cupolae
1 truncated tetrahedron
Total: 62 cells.
I'm not 100% sure if the dichoral angles work out correctly, but it seems that if we cap the bottom of the polychoron with x3x3o||o3x3o, the triangular cupolae would close up into more cuboctahedra, and we would obtain your construction with octahedron at the bottom. I'm just unsure if the dichoral angles would work out, though. I'll try to extend this and see.
In any case, looking at the cell configuration, it seems that it may not be possible to construct the analogue with octahedral symmetry after all -- because you would end up with 4 tetrids surrounding a cube, which would make a gap containing 4 pentagons surrounding a square. However, there is no Johnson solid I know of that has 4 pentagons surrounding a square. According to analogy, it would seem that we'd need 3D square teddies in order to fill in the gaps, but square teddies are non-CRF because they have √2-edges. Similarly, it doesn't seem possible to extend this construction to icosahedral symmetry either -- the corresponding gaps would require pentagonal teddies (bisected dodecahedra), and again they are non-CRF because of the phi-edges.
1+4 = 5 x3o3x
6+4+12+12 = 34 triangular prisms
4+4 = 8 J63's (teddies)
4 J83's (tetrids)
6 J62's (mibdies)
4 triangular cupolae
1 truncated tetrahedron
Total: 62 cells.
I'm not 100% sure if the dichoral angles work out correctly, but it seems that if we cap the bottom of the polychoron with x3x3o||o3x3o, the triangular cupolae would close up into more cuboctahedra, and we would obtain your construction with octahedron at the bottom. I'm just unsure if the dichoral angles would work out, though. I'll try to extend this and see.
In any case, looking at the cell configuration, it seems that it may not be possible to construct the analogue with octahedral symmetry after all -- because you would end up with 4 tetrids surrounding a cube, which would make a gap containing 4 pentagons surrounding a square. However, there is no Johnson solid I know of that has 4 pentagons surrounding a square. According to analogy, it would seem that we'd need 3D square teddies in order to fill in the gaps, but square teddies are non-CRF because they have √2-edges. Similarly, it doesn't seem possible to extend this construction to icosahedral symmetry either -- the corresponding gaps would require pentagonal teddies (bisected dodecahedra), and again they are non-CRF because of the phi-edges.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Hehe, just while you posted these nice pics of the shortened version, I myself also found out that this is possible. Thus my former solution was just its blend with an additional attached tut||oct to the one end.
--- rk
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Are you sure the result is still CRF? I tried computing the coordinates for the version lengthened with tut||oct, but it doesn't seem to be convex. (The convex hull introduces new non-CRF lacing cells to the oct.) Not sure if it's actually not possible, or I made a mistake somewhere?
My polytope viewer says that the dichoral angle between the tut and the 3cups is approx 164.4775°. What's the dichoral angle of tut to 3cup in tut||oct?
My polytope viewer says that the dichoral angle between the tut and the 3cups is approx 164.4775°. What's the dichoral angle of tut to 3cup in tut||oct?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
The dichoral angle of tricu(6)tut in ox3xx3o&#x is identical to that of tet(3)tet in ox3oo3oo&#x, aka in pen.
(As the former is just an expansion of the latter.) Thence it is arccos(1/4) = 75.522488 degrees.
--- rk
(As the former is just an expansion of the latter.) Thence it is arccos(1/4) = 75.522488 degrees.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
And here finally is its full Dynkin symbol:
(Cf. esp. the layers which contained those unknown quantities B,C,D.)
--- rk
- Code: Select all
xxFVF(Vx)fox-3-ofxxf(oF)xxx-3-xoooo(xo)xfo-&#xt
(Cf. esp. the layers which contained those unknown quantities B,C,D.)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Thanks for the full CD symbol!! That's very helpful.
Anyway, given that the dichoral angles between the tut and 3cups and in ox3xx3o&#x don't add up to 180° (it exceeds 180°), it would seem like your extended version won't be CRF. (Or am I missing something?)
(Or am I missing something?)
Anyway, given that the dichoral angles between the tut and 3cups and in ox3xx3o&#x don't add up to 180° (it exceeds 180°), it would seem like your extended version won't be CRF.
 (Or am I missing something?)
(Or am I missing something?)- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Here are the coordinates:
where φ=(1+√5)/2 is the Golden Ratio, apacs means "all permutations and changes of sign", apecs means "all permutations and even changes of sign", and ~ means vector concatenation (this notation is mainly so I can concisely express vertex layers in terms of apacs and apecs while assigning the height of the layer separately).
- Code: Select all
apacs<0, √2, √2> ~ <-3*φ²/√2>
apecs<1/√2, 1/√2, (1+2*φ)/√2> ~ <-(3*φ+2)/√2>
apecs<φ²/√2, φ²/√2, (φ+3)/√2> ~ <-2*φ²/√2>
apecs<φ*√2, φ*√2, φ²*√2> ~ <-φ²/√2>
apecs<φ²/√2, φ²/√2, (1+3*φ)/√2> ~ <0>
apecs< 1/√2, 1/√2, (3+2*φ)/√2> ~ <φ/√2>
apecs<(2*φ-1)/√2, (2*φ+1)/√2, (2*φ+1)/√2> ~ <φ/√2>
apecs<1/(φ*√2), φ²/√2, (φ+3)/√2> ~ <2*φ/√2>
apecs<-φ/√2, φ/√2, (φ+2)/√2> ~ <(2*φ+1)/√2>
apecs<1/√2, 1/√2, 3/√2> ~ <3*φ/√2>
where φ=(1+√5)/2 is the Golden Ratio, apacs means "all permutations and changes of sign", apecs means "all permutations and even changes of sign", and ~ means vector concatenation (this notation is mainly so I can concisely express vertex layers in terms of apacs and apecs while assigning the height of the layer separately).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Hadn't checked ...
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Any ideas on how to name this CRF?  Currently I'm thinking of something like "cantellated ursachoron" or "decagonal ursachoron", but they don't sound that good. Maybe "fat teddy", but then the construction isn't really directly related to teddi. Maybe Jonathan may have some better ideas?
Currently I'm thinking of something like "cantellated ursachoron" or "decagonal ursachoron", but they don't sound that good. Maybe "fat teddy", but then the construction isn't really directly related to teddi. Maybe Jonathan may have some better ideas?
Maybe "magnaursachoron"? (Latin for "big bear" ).
).
 Currently I'm thinking of something like "cantellated ursachoron" or "decagonal ursachoron", but they don't sound that good. Maybe "fat teddy", but then the construction isn't really directly related to teddi. Maybe Jonathan may have some better ideas?
Currently I'm thinking of something like "cantellated ursachoron" or "decagonal ursachoron", but they don't sound that good. Maybe "fat teddy", but then the construction isn't really directly related to teddi. Maybe Jonathan may have some better ideas?Maybe "magnaursachoron"? (Latin for "big bear"
 ).
).- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
"Magnaursachoron" sounds quite good to me.
"Cell-expanded (axially-)tetrahedral ursachoron" might work as well.
Thought a bit about its building principle.
But then we also have mibdi. That one is implemented within the magnaursachoron as some (upper) part of the a . c tower-stack (in fact as xfox2oxfo&#xt). Thus the aimed for extension would at least ask for the existance of a . c-P-o resp. a . c-P-x. And as the latter is a "normal" partial Stott expansion of the former, we'll just have to look for that first ones only. (The single exceptional case from the latter ones, xfox-2-oxfo-2-xxxx-&#xt, here clearly does exist: it just is the mibdi prism.)
Thus, what then would be xfox-2-oxfo-P-oooo-&#xt (P=3,4,5)? - I will have to take a look into these...
--- rk
"Cell-expanded (axially-)tetrahedral ursachoron" might work as well.
Thought a bit about its building principle.
- The teddi, being the single ursahedron, when considered as tower-stacking of a-3-b layers, uses both non-vanishing a and b in at least some of its layers. (Thus we cannot freely vary that -3-.)
- But we were able to extend that into 4D as the same stacking either as a-3-b-P-o (for P=3,4,5) or as a-3-b-P-x (for P=2,3,4,5). (And even beyond as a-3-b-P-o-Q-o etc.)
- That new found fellow now looks as being quite similar a "single" (magna-)ursachoron with tower-stacking a-3-b-3-c, where each a, b, and c is non-vanishing in at least some layers. (Therefore we cannot freely vary any of these -3-'s.)
- But again we could consider a-3-b-3-c-P-o (for P=3,4,5) and a-3-b-3-c-P-x (for P=2,3,4,5). And, in fact, the contained teddies of the magnaursachoron were implemented as b-3-c in the correct orientation. Thus the resulting 4D facets b-3-c-P-o resp. b-3-c-P-x all look valid by means of the above already said.
But then we also have mibdi. That one is implemented within the magnaursachoron as some (upper) part of the a . c tower-stack (in fact as xfox2oxfo&#xt). Thus the aimed for extension would at least ask for the existance of a . c-P-o resp. a . c-P-x. And as the latter is a "normal" partial Stott expansion of the former, we'll just have to look for that first ones only. (The single exceptional case from the latter ones, xfox-2-oxfo-2-xxxx-&#xt, here clearly does exist: it just is the mibdi prism.)
Thus, what then would be xfox-2-oxfo-P-oooo-&#xt (P=3,4,5)? - I will have to take a look into these...
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Very interesting idea! I tried to construct xfox-2-oxfo-P-oooo-&#xt for the case P=4, but found that the last layer x2o4o is far too small to have unit lacing edges from the previous layer, so the mibdis cannot form.
Using the method of completing the pentagon, however, I managed to figure out that x2o4q is the correct configuration for completing the mibdis.
However, now there is a problem on the far side, in that it's not clear how to close up the x2o4q in a CRF way. I did notice that the last two layers on the .4. side hints at an incomplete cuboctahedron (x4o || o4q), and I tried to close this up by completing the square. Unfortunately, the closure would require something like v2x4o, and the gap of size v is too narrow to have a CRF closure. Furthermore, there are also the lacing edges from o2f4o to x2o4q which are non-CRF; currently they produce various scalene tetrahedral cells and some (non-CRF) pyramids.
This doesn't yet rule out the possibility of CRF closure on the starting configuration (4 mibdis + 2 square pyramids), but it seems to indicate that any CRF closure will need to be bigger than just another 1-2 vertex layers. Perhaps there's a way to add more cells to "cover over" the q edges so that it will close up in a CRF way.
I haven't tried the P=3 or P=5 cases yet, but my current intuition indicates that probably one of those cases should have a simpler CRF closure than the P=4 case.
Using the method of completing the pentagon, however, I managed to figure out that x2o4q is the correct configuration for completing the mibdis.
However, now there is a problem on the far side, in that it's not clear how to close up the x2o4q in a CRF way. I did notice that the last two layers on the .4. side hints at an incomplete cuboctahedron (x4o || o4q), and I tried to close this up by completing the square. Unfortunately, the closure would require something like v2x4o, and the gap of size v is too narrow to have a CRF closure. Furthermore, there are also the lacing edges from o2f4o to x2o4q which are non-CRF; currently they produce various scalene tetrahedral cells and some (non-CRF) pyramids.
This doesn't yet rule out the possibility of CRF closure on the starting configuration (4 mibdis + 2 square pyramids), but it seems to indicate that any CRF closure will need to be bigger than just another 1-2 vertex layers. Perhaps there's a way to add more cells to "cover over" the q edges so that it will close up in a CRF way.
I haven't tried the P=3 or P=5 cases yet, but my current intuition indicates that probably one of those cases should have a simpler CRF closure than the P=4 case.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
I'm still trying to wrap my head around this magnaursachoron.
In the meantime, I created the tridiminished rhodoperihedron page and added a visual comparison between it and teddi, hoping that this will help.
How does the magnaursachoron compare with the expanded pyroursachoron? What makes them different? Is there any chance you could do some renders of the latter? (Only the expanded aeroursachoron has an image; the hydro variant is also missing an image.)
Since both are expansions of the pyroursachoron, what is the difference between the types of expansions performed? In 3D, do they collapse to the same operation, or does one become invalid / produce non-CRFs?
Could you do renders highlighting each cell type one at a time for each of the 3 views you previously posted? Maybe also a render showing the same 4D side view as the last one (the one that's on the wiki), but rotated in 3D so that you are looking down from the top? (So the 4D top is at the front of the 3D viewpoint and the 4D bottom is at the back.)
Sorry for the silly number of render requests, I'm just really excited you found a new figure
In the meantime, I created the tridiminished rhodoperihedron page and added a visual comparison between it and teddi, hoping that this will help.
How does the magnaursachoron compare with the expanded pyroursachoron? What makes them different? Is there any chance you could do some renders of the latter? (Only the expanded aeroursachoron has an image; the hydro variant is also missing an image.)
Since both are expansions of the pyroursachoron, what is the difference between the types of expansions performed? In 3D, do they collapse to the same operation, or does one become invalid / produce non-CRFs?
Could you do renders highlighting each cell type one at a time for each of the 3 views you previously posted? Maybe also a render showing the same 4D side view as the last one (the one that's on the wiki), but rotated in 3D so that you are looking down from the top? (So the 4D top is at the front of the 3D viewpoint and the 4D bottom is at the back.)
Sorry for the silly number of render requests, I'm just really excited you found a new figure

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: A different way to expand an ursatope?
Actually, I think the whole "expansion" thing is a bit misleading. While it's certainly true that you can get from J62 (tridiminished icosahedron) to J83 (tridiminished rhombicosidodecahedron) via some kind of modified Stott expansion, the magna ursachoron can't be derived via a straight expansion, AFAICT. Basically, what I did was to exploit the fact that, due to the relationship between J62 and J83, the angles between the top triangular face and the pentagons in the J62 are the same as the angles between the top triangular face and the decagons in J83 (albeit in the case of J83, there are intervening faces in between). Due to this relationship, you could think of J83 as a J62 with some edges bevelled into squares and a few corners cut off -- the configuration of faces changes, but the overall solid bulk has approximately the same kind of shape. That means that when you fold J83's into 4D, they should result in the same dichoral angles as the J62's in the ursachora.
In other words, the "slope" of the J83's in the magnaursachoron relative to the chosen vertical axis is the same as the "slope" of the J62's in the tetrahedral ursachoron. So there ought to be some way to make a CRF closure of this tetrahedral configuration of J83's that resembles the closure of the tetrahedral ursachoron. The analogy ends there, however, because the magnaursachoron has quite a bit more cells that are needed to fill in all the gaps, and not all of them have direct analogues to the cells in the tetrahedral ursachoron. The relationship between the two is also not that straightforward, AFAICT, because I didn't really perform the construction as some kind of edge-truncation of the tetrahedral teddy, but started with 4 J83's in tetrahedral formation as the basis, and then tried to fill in the cells so that it would close up in a CRF way. So the relationship is rather complex, and probably should be thought more as a variety of different local Stott expansions of cells assembled together, rather than some global operation that derives the magnaursachoron directly from the tetrahedral teddy.
As for the renders: cell-by-cell renders are rather tedious, I'll have to postpone that and see if I can get some time this weekend to do them. But rotating the 3D view is easy, lemme just run that through...
Here's the view of the 3rd projection from the top:
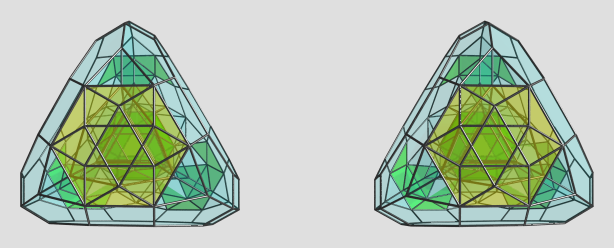
It's not very insightful, unfortunately, due to the difficulty in seeing where the cells in the middle are.
Here's a look at the same projection, but from the bottom in 3D:
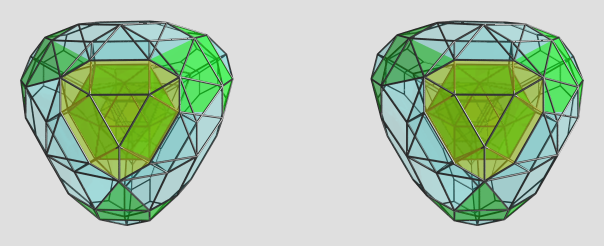
Again, not very insightful, but I suppose it does help you to see the (very!) slight fatness of the polytope toward the bottom, compared to the top.
In other words, the "slope" of the J83's in the magnaursachoron relative to the chosen vertical axis is the same as the "slope" of the J62's in the tetrahedral ursachoron. So there ought to be some way to make a CRF closure of this tetrahedral configuration of J83's that resembles the closure of the tetrahedral ursachoron. The analogy ends there, however, because the magnaursachoron has quite a bit more cells that are needed to fill in all the gaps, and not all of them have direct analogues to the cells in the tetrahedral ursachoron. The relationship between the two is also not that straightforward, AFAICT, because I didn't really perform the construction as some kind of edge-truncation of the tetrahedral teddy, but started with 4 J83's in tetrahedral formation as the basis, and then tried to fill in the cells so that it would close up in a CRF way. So the relationship is rather complex, and probably should be thought more as a variety of different local Stott expansions of cells assembled together, rather than some global operation that derives the magnaursachoron directly from the tetrahedral teddy.
As for the renders: cell-by-cell renders are rather tedious, I'll have to postpone that and see if I can get some time this weekend to do them. But rotating the 3D view is easy, lemme just run that through...
Here's the view of the 3rd projection from the top:

It's not very insightful, unfortunately, due to the difficulty in seeing where the cells in the middle are.
Here's a look at the same projection, but from the bottom in 3D:

Again, not very insightful, but I suppose it does help you to see the (very!) slight fatness of the polytope toward the bottom, compared to the top.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
On a tangential note, due to the same correspondence between J62 and J83, I have been speculating for a while now that it should be possible to create a analogue of bidex with J83's instead of teddies, with suitable filler cells to close up the gaps. I'm pretty sure this should be some diminishing of x5o3x3o or x5o3x3x, but so far I haven't dared to attempt constructing it just yet, due to the sheer number of elements that must (currently) be manually selected and modified by hand. The resulting polychoron should have 48 J83's in the same arrangement as the teddies in bidex. (In fact, I'm pretty sure this diminishing must be already known due to its obvious analogy to bidex, probably by Jonathan Bowers and/or Klitzing et al.)
Another potential CRF I'm thinking of is the expanded magnaursachoron: i.e., what if we start with 4 J83's in tetrahedral formation, but instead of touching each other at the decagons, insert decagonal prisms between them. I'm not 100% sure it's possible to close this up in a CRF way, but it does seem quite promising at first glance.
(In fact, now I feel tempted to examine every CRF we've ever found that sports teddies as cells, and substitute J83's for the teddies and see if the result is CRF-able. )
)
Another potential CRF I'm thinking of is the expanded magnaursachoron: i.e., what if we start with 4 J83's in tetrahedral formation, but instead of touching each other at the decagons, insert decagonal prisms between them. I'm not 100% sure it's possible to close this up in a CRF way, but it does seem quite promising at first glance.
(In fact, now I feel tempted to examine every CRF we've ever found that sports teddies as cells, and substitute J83's for the teddies and see if the result is CRF-able.
 )
)- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
quickfur wrote:In other words, the "slope" of the J83's in the magnaursachoron relative to the chosen vertical axis is the same as the "slope" of the J62's in the tetrahedral ursachoron. So there ought to be some way to make a CRF closure of this tetrahedral configuration of J83's that resembles the closure of the tetrahedral ursachoron. The analogy ends there, however, because the magnaursachoron has quite a bit more cells that are needed to fill in all the gaps, and not all of them have direct analogues to the cells in the tetrahedral ursachoron. The relationship between the two is also not that straightforward, AFAICT, because I didn't really perform the construction as some kind of edge-truncation of the tetrahedral teddy, but started with 4 J83's in tetrahedral formation as the basis, and then tried to fill in the cells so that it would close up in a CRF way. So the relationship is rather complex, and probably should be thought more as a variety of different local Stott expansions of cells assembled together, rather than some global operation that derives the magnaursachoron directly from the tetrahedral teddy.
This was exacltly why I prefixed that attribute accordingly, cf.
Klitzing wrote:"Magnaursachoron" sounds quite good to me.
"Cell-expanded (axially-)tetrahedral ursachoron" might work as well.
I.e. expansions does not apply to the polchoral body. Rather it is to be considered cellwise here.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:On a tangential note, due to the same correspondence between J62 and J83, I have been speculating for a while now that it should be possible to create a analogue of bidex with J83's instead of teddies, with suitable filler cells to close up the gaps. I'm pretty sure this should be some diminishing of x5o3x3o or x5o3x3x, but so far I haven't dared to attempt constructing it just yet, due to the sheer number of elements that must (currently) be manually selected and modified by hand. The resulting polychoron should have 48 J83's in the same arrangement as the teddies in bidex. (In fact, I'm pretty sure this diminishing must be already known due to its obvious analogy to bidex, probably by Jonathan Bowers and/or Klitzing et al.)
Well, indeed, I already considered an expanded version of sadi (= idex): the icositetra-diminishing of sidpixhi (x3o3o5x), idsid pixhi.
And also one of bidex: the bi-icositetra-diminishing of sidpixhi, bidsid pixhi.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
bidsid pixhi then accordingly has 48 tedrids.
Forgot to mention the icositetra-diminishing of srahi (o3x3o5x), idsrahi. That one then has 96 tedrids.
--- rk
Forgot to mention the icositetra-diminishing of srahi (o3x3o5x), idsrahi. That one then has 96 tedrids.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:(In fact, now I feel tempted to examine every CRF we've ever found that sports teddies as cells, and substitute J83's for the teddies and see if the result is CRF-able.)
Got a promising idea! What then about teddi || ... || tedrid?
Thus let's have a closer look. Anyone knows: teddi is the tridiminished ike. And tedrid is the tridiminished rhombicosidodecahedron. But there is no segmentochoron ike || srid. At least not outside of hyperbolic geometries. For that would require longer lacings than unity. But we could place a further layer inbetween.
Thus let's start with rox (o3x3o5o). The bistratic ike-first cap of rox then just is ike || id || srid. Or as a lace city in trigonal subsymmetry it looks like:
- Code: Select all
x3o o3f f3o o3x ike
o3x x3f F3o f3f o3F f3x x3o id
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f oF3Vx f3F V3x x3V F3f Vx3oF f3x o3x srid
As such it is nothing but a stack of 2 well-known segmentochora. But what, if we'd diminish that cap in a 3fold way, such that the topmost layer deforms into a teddi, the bottom one into tedrid, and the medial one in some polyhedron, which not necessarily has to be CRF (aka Johnson solid).
Here is what this new idea of mine has identified:
- Code: Select all
x3o f3o o3x teddi
o3x F3o f3x x3o
F=ff=x+f=2x+v,
V=F+v=2f=2x+2v
x3o x3f F3x V3x F3f Vx3oF f3x o3x tedrid
The former segmentochoral stack is known to have for lacing cells octs and peppies (J2) resp. octs, squippies (J1), and paps. In this bistratic stack these peppies and paps recombine into gyepips (J11). Thus we would not wonder if these now get further diminished and teddies (J63) or even mibdies (J62) would occur.
The decagonal faces of the bottom tedrid (J83) moreover has to be aligned with the pentagonal faces of the top teddi (J63). Accordingly in the medial layer we'll have an inverted f-pentagon. And the total cell at these places will be a pero (J6) each.
Will still have to count out the different cells. (And to elaborate its incidence matrix, for sure.) Whereas, the geometry already is perfect clear. - Perhaps quickfur in the meantime comes up with some nice pics?
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
Aggregated now the corresponding cell count. 'T is:
And, for sure, the same diminishing concept would hold too, when considering any other srid-diminishing as a base of this bistratic rox cap. I.e. we also could derive some
--- rk
- teddies (J63): 1+3+3 = 7
- octs: 1+3+1+1+3+1 = 10
- peroes (J6): 3
- mibdies (J62): 3
- squippies (J1): 3+3+6+3 = 15
- tedrid (J83): 1
And, for sure, the same diminishing concept would hold too, when considering any other srid-diminishing as a base of this bistratic rox cap. I.e. we also could derive some
- ike || id || srid = bistratic rox cap
- gyepip (J11) || ... || dirid (J76)
- pap || ... || pabidrid (J80)
- mibdi (J62) || ... || mabidrid (J81)
- teddi (J63) || ... || tedrid (J83) (the one described above & within the last post)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: A different way to expand an ursatope?
quickfur wrote:In any case, looking at the cell configuration, it seems that it may not be possible to construct the analogue with octahedral symmetry after all -- because you would end up with 4 tetrids surrounding a cube
Hang on - where does the cube come from? I don't see any tetrahedra in the tetrahedral magnaursachoron...
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: A different way to expand an ursatope?
Keiji wrote:quickfur wrote:In any case, looking at the cell configuration, it seems that it may not be possible to construct the analogue with octahedral symmetry after all -- because you would end up with 4 tetrids surrounding a cube
Hang on - where does the cube come from? I don't see any tetrahedra in the tetrahedral magnaursachoron...
Right now there's a triangular prism between every 3 adjacent tetrids. If there were 4 adjacent tetrids, as would be the case if we had octahedral symmetry, then you'd need cubes in the same position to fill in the gaps.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: A different way to expand an ursatope?
Ah, right. Wasn't thinking of them being square prisms.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
102 posts
• Page 1 of 4 • 1, 2, 3, 4
Who is online
Users browsing this forum: No registered users and 53 guests
