Klitzing wrote:[...]The upper pentagons of the first picture would obviously join the thawro cells to peppies.
Correct.
:?: : But for the frontal pentagonal struts this is much lesser "obvious". But I guess that there too one tet face, 2 thawro faces and 2 squippy faces would connect to a further peppy, and that this very peppy then would connect to a second peppy, which in the second picture then would connect to 2 mibdi faces and to 3 tet faces. Right? I even suppose that the angle between these 2 peppies at the pentagon would neither be 180 degrees, nor such that it could be replaced by a 5 tet rosette? Right or wrong?
Yes, these pentagonal pyramids are in pairs, with one of the pair on the near side (first image) and the other on the far side (second image). They cannot be 180° to each other, because otherwise they'd be pentagonal
bipyramids.
Furthermore, since these models are produced by a convex hull algorithm, in no case can a pair of pentagonal pyramids be replaced with a rosette of 5 tetrahedra: that is only possible if the dichoral angle between the two pentagonal pyramids are > 180°. Or to be precise, the dichoral angle will have to be exactly (360° - A), where A = dichoral angle of pentagonal pyramids in the segmentochoron pentagonal_pyramid || point.
Basically, the analogy here is with two isosceles triangles joined at a phi-edged base (resp. pentagonal pyramids joined at the pentagon). If their dichoral angle is < 180°, that is, the phi-edged base (resp. pentagonal face) protrudes inwards towards the centroid of the polytope, that is, they are concave, then you can close them up with two triangles (resp. rosette of 5 tetrahedra) to make the result convex. If they are 180° to each other, they form a phi-rhombus (resp. pentagonal bipyramid): the phi-edge is coplanar with the triangles (resp. pentagonal face with the two pyramids) and becomes internal to a single merged face. If their dichoral angle is > 180°, that is, the phi-edged base (resp. pentagonal face) protrudes
outwards, then they form a wedge on the surface of the polytope, and any closure with two triangles (resp. rosette of 5 tetrahedra) will be internal to the polytope -- they will lie
behind the phi-scaled edge (resp. pentagonal face).
Then upon the augmentation, I did mention. That is, adding vertices atop / within the teddies resp. mibdis:
Klitzing wrote:In fact, it thus rather looks like that these 8 diminishings come completely independent of that thawro-ing here. Then we would have a
thawro-ed 2/6-lune of ex (only through the thawro-ing this lune itself becomes CRF!), and several diminishings thereof. - Yours then just is an octadiminishing. - Right?


: Would that then replace the so far pentagons at the teddi-mibdi join resp. at the mibdi-mibdi join by 5 tet rosettes or rather by 2 peppy pairs (or even by a single pedpy?) at each occurency?
I believe what happens is that the augments on adjacent J62 / J63's will become non-convex, that is, the pentagonal pyramids introduced by the augments will have dichoral angle > 180°. The convex hull algorithm would then, in effect, cover over these concave gaps with rosettes of 5 tetrahedra. Or rather, it inserts pentagonal_pyramid||point segmentochora between the augments so that the result becomes convex.
My guess here would be that the former question about the peppy-peppy join (between those pics) the existance of the changed base vertices of the thawroes might imply some strange dihedral angles and so the 5 tet rosette would come out of scope here. But for the second cases, as being then parts of an ex sub-structure, these 5 tet rosettes might be implied. Note moreover that we would consider CRFs.
Both are just guesses. I did not calculate any dihedral angle here. But you might simply derive that from your vertex calculations... And thus could answer these questions much more quickly?
Well, the peppy-peppy join here is basically an indication that the two halves are thin caps of the 600-cell, where after stripping off the rosettes of 5 tetrahedra, the pentagonal pyramids thus exposed still have < 90° dichoral angle with the bisecting hyperplane. So they can be glued together with two pentagonal pyramids exposed on the surface of the result. If they were exactly 90°, then putting the two halves together will produce pentagonal bipyramids; if they were > 90°, then putting the halves together will be non-convex, and the convex hull algorithm will introduce lacing edges between the tips of the pentagonal pyramids, which, in effect, inserts the rosettes of 5 tetrahedra (and the pentagonal pyramids become internal to the polytope).






 I'm guessing I should post that in a different thread once I get some nice renders up (and work out the lace city -- I have the coordinates but need to sit down and work out where each node in the lace city should go).
I'm guessing I should post that in a different thread once I get some nice renders up (and work out the lace city -- I have the coordinates but need to sit down and work out where each node in the lace city should go). The next thing you know, we're gonna be making tetrahedron-centered 600-cell lunes, perhaps made CRF by pocuro'ing?
The next thing you know, we're gonna be making tetrahedron-centered 600-cell lunes, perhaps made CRF by pocuro'ing? 
 : But for the frontal pentagonal struts this is much lesser "obvious". But I guess that there too one tet face, 2 thawro faces and 2 squippy faces would connect to a further peppy, and that this very peppy then would connect to a second peppy, which in the second picture then would connect to 2 mibdi faces and to 3 tet faces. Right? I even suppose that the angle between these 2 peppies at the pentagon would neither be 180 degrees, nor such that it could be replaced by a 5 tet rosette? Right or wrong?
: But for the frontal pentagonal struts this is much lesser "obvious". But I guess that there too one tet face, 2 thawro faces and 2 squippy faces would connect to a further peppy, and that this very peppy then would connect to a second peppy, which in the second picture then would connect to 2 mibdi faces and to 3 tet faces. Right? I even suppose that the angle between these 2 peppies at the pentagon would neither be 180 degrees, nor such that it could be replaced by a 5 tet rosette? Right or wrong?
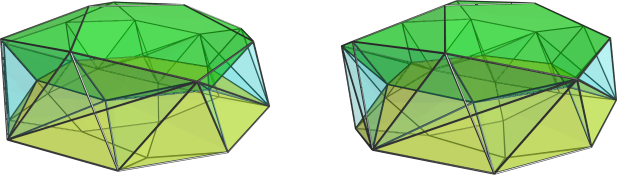
 You can see the teddi's here. Unfortunately there's an f-edge here. The f-edge can be seen in the lace-city as the connection between F3o and o3F. In other lace-cities this f-edge is internal to some pentagon, but at the 1/6-lune all pentagons to which this f-edge is internal are destroyed. This means it gets revealed, and the polytope isn't CRF. Of course it could be possible that by extruding pyramids on the teddi's, something awesome makes it CRF again, but I doubt that.
You can see the teddi's here. Unfortunately there's an f-edge here. The f-edge can be seen in the lace-city as the connection between F3o and o3F. In other lace-cities this f-edge is internal to some pentagon, but at the 1/6-lune all pentagons to which this f-edge is internal are destroyed. This means it gets revealed, and the polytope isn't CRF. Of course it could be possible that by extruding pyramids on the teddi's, something awesome makes it CRF again, but I doubt that.