Augmented polyhedral prisms
88 posts
• Page 3 of 3 • 1, 2, 3
Re: Augmented polyhedral prisms
First of all, these values of student91 would reflect the required angles of the trips attached to the 4 polar triangles. The other ones would ask for the third dihedral angle, not mentioned in his post.
The required value of about 73 degrees at a square can be matched easily by several small attaching cells. But the required value of 58 cannot be matched by any cell!
This is simply because the "sharpest" segmentochoron with one trip base and without a retrograde top base clearly is the trippy = pt || trip. And that one already has dihedral angles of
• at {4} between squippy and trip: arccos(sqrt[1/6]) = 65.905157°
At least for straight segmentochora. If you look at sheered segmentochora (thus asking for a dimensional degenerate top base!) you might be more lucky.
But the case of a point for top base already is done by trippy. The case of a line segment there is done either by bidrap or by tepe (depending on relative orientation). And the case of a triangle for opposing base is done by triddip resp. traf = K-4.6 (depending on relative gyration). - Therin only bidrap implements some shift of the degenerate base. But none of these would bow to the above requirements.
This then concludes the proof that a snadow prism cannot be augmented.
--- rk
The required value of about 73 degrees at a square can be matched easily by several small attaching cells. But the required value of 58 cannot be matched by any cell!
This is simply because the "sharpest" segmentochoron with one trip base and without a retrograde top base clearly is the trippy = pt || trip. And that one already has dihedral angles of
• at {4} between squippy and trip: arccos(sqrt[1/6]) = 65.905157°
At least for straight segmentochora. If you look at sheered segmentochora (thus asking for a dimensional degenerate top base!) you might be more lucky.
But the case of a point for top base already is done by trippy. The case of a line segment there is done either by bidrap or by tepe (depending on relative orientation). And the case of a triangle for opposing base is done by triddip resp. traf = K-4.6 (depending on relative gyration). - Therin only bidrap implements some shift of the degenerate base. But none of these would bow to the above requirements.
This then concludes the proof that a snadow prism cannot be augmented.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
But then what about 3 snadows adjoined mutually around their sharp angles (more are impossible)?
Could that be continued somehow? (Possibly with tets at the neighbouring triangles and perhaps further snadows at the opposite sharp angle as well?)
(Okay, that won't be an augmented prism, so should be placed within a different thread, I suppose...)
--- rk
Could that be continued somehow? (Possibly with tets at the neighbouring triangles and perhaps further snadows at the opposite sharp angle as well?)
(Okay, that won't be an augmented prism, so should be placed within a different thread, I suppose...)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
That won't work either I suppose, the distance between the outer vertices will become very weird, making it impossible for one of the known Johnson solids to fit inbetween. Setting more than one solid inbetween will result in non-convexity
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Augmented polyhedral prisms
Well, my original idea here was, kind of something similar to the great antiprism or some weird expansion of a duoprism, using the snadows as the separating elements (along with possibly some other stuff) ...
--- rk
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
It may be hard for a single Johnson to fit between the "weird distances" of the outer vertices, but what if we have several smaller pieces that confer more flexibility? Or do we still run into the same problem eventually because 4D vertices must be rigid?
Also, if there's not enough space between, say, a floret of 3 snadows around an edge to insert bridging cells, what if we Stott-expand the configuration by inserting triangular prisms between the snadows? Though that does have the wrinkle of introducing square faces that must join to something else, which may limit the possibilities. But OTOH, it may expand the possibilities because then we'd be able to bring, say, squippies into play where tetrahedral dihedral angles may prove insufficient.
Also, if there's not enough space between, say, a floret of 3 snadows around an edge to insert bridging cells, what if we Stott-expand the configuration by inserting triangular prisms between the snadows? Though that does have the wrinkle of introducing square faces that must join to something else, which may limit the possibilities. But OTOH, it may expand the possibilities because then we'd be able to bring, say, squippies into play where tetrahedral dihedral angles may prove insufficient.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
Klitzing wrote:Putting it all together, ...
The second type of variation is limited by ... P=2 for the second, where the polychora become dimensionally degenerate (becoming J51 and J57, resp. their prisms). Accordingly we have here the following bunch of valide CRFs:
...
oa3xo3oo xo&#zx = ope + 4 (alternate) trippies
oa3xo3xx xo&#zx = tuttip + 4 tripufs
xb3xo3oo xo&#zx = tuttip + 4 trippies
xb3xo3xx xo&#zx = tope + 4 (alternate) tripufs
(where a = (2+sqrt(10))/3 = 1.720759, b = a+x = 2.720759)
oa3xo4oo xo&#zx = cope + 6 cubpies
oa3xo4xx xo&#zx = ticcup + 6 (ortho) squipufs
xb3xo4oo xo&#zx = tope + 6 cubpies
xb3xo4xx xo&#zx = gircope + 6 (ortho) squipufs
(where a = w/q = 1.707107, b = a+x = 2.707107)
of3xo5oo xo&#zx = iddip + 12 peppies
of3xo5xx xo&#zx = tiddip + 12 (ortho) pepufs
xF3xo5oo xo&#zx = tipe + 12 peppies
xF3xo5xx xo&#zx = griddip + 12 (ortho) pepufs
(where F = ff = f+x)
...
Just like to mention that the highlighted 3 together with the above mentioned J51-prism, which then is nothing but tisdip + 3 squippyp (or: line || cube, i.e. di-puf), already was looming up way back in November of 2012, cf. that post (within the 2nd half of it). I just re-found that one by hazard this weekend!

In those days I still was not aware of the full shape, not knowing all their dihedrals, even was asking for coords. So, by means of those student91-style tegum sum notations provided in this recent post (i.e. oa3xoPxx xo&#zx), together with the also provided respective measures "a", we are a big step ahead now.

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
Just wanted to state that username recently found that wacope (J86-p) could be blended with a cubpy!
This indeed is valide, as the respective dihedrals of wacope would be the same as those of waco itself
and the base dihedrals of cubpy surely is lesser than that of squippy (J1). That is, this newly found CRF
surely exists, whenever the 3D blend of waco (J86) and squippy (J1) would exist. And that latter
one clearly is well-known: it is nothing but auwaco (J87).
--- rk
This indeed is valide, as the respective dihedrals of wacope would be the same as those of waco itself
and the base dihedrals of cubpy surely is lesser than that of squippy (J1). That is, this newly found CRF
surely exists, whenever the 3D blend of waco (J86) and squippy (J1) would exist. And that latter
one clearly is well-known: it is nothing but auwaco (J87).
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
Klitzing wrote:[...]
That is, this newly found CRF surely exists, whenever the 3D blend of waco (J86) and squippy (J1) would exist.
[...]
In fact, we can specify a tighter criterion here. The height of a cubical pyramid is 1/2 (given unit edges); given any convex polyhedron P with a square face of unit edge length, the P-prism augmented with a cubical pyramid projects to P augmented with a square pyramid of height 1/2 (this is shallower than the CRF square pyramid, which has height 1/√2). If this augmentation is convex, then the augmentation of the P-prism with a cubical pyramid must also be convex. If P is CRF, then the augmentation of the P-prism must also be CRF.
In fact, this criterion is so straightforward that it's probably possible to quickly comb through 3D CRFs with square faces and discover which augmentations of their corresponding 4D prisms would be CRF.
Last edited by quickfur on Thu Feb 04, 2021 4:23 pm, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
Just found another one: the augmented J89 prism. This one is particularly interesting because it falls only under the tighter criterion I stated above; there is no CRF augmentation of J89 in 3D. The dihedral angle between the middle square and its adjacent triangles is 133.972805°, which is barely shy of 135°. This means an augment with a height 1/2 square pyramid will just barely stay convex, the dihedral angle at its base being 45°. This in turn translates to a dichoral angle of 178.972805° between the lateral square pyramids of the augment of the augmented J89 prism with the triangular prisms connecting the triangles adjacent to the J89 cells' bottom square faces: it's only 1° away from being coplanar!!
Here's a render of this cutie:
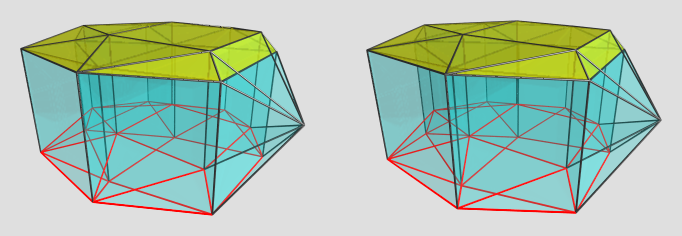
This is not quite a perpendicular viewpoint; I moved the 4D viewpoint slightly up so that the J89 cells (yellow on the near side, red outline on the far side) would have some "volume" in the projection image. The augment is on the right. The 178.97° dichoral angle occurs between the triangular prism in the front of the projection image, and the square pyramid on the front right.
Here are the coordinates:
A is the root of the following polynomial between 0.20 and 0.22:
26880x10 + 35328x9 - 25600x8 - 39680x7 + 6112x6 + 13696x5 + 2128x4 - 1808x3 - 1119x2 + 494x - 47 = 0
Approximate value is A = 0.216844815713457.
Here's a render of this cutie:

This is not quite a perpendicular viewpoint; I moved the 4D viewpoint slightly up so that the J89 cells (yellow on the near side, red outline on the far side) would have some "volume" in the projection image. The augment is on the right. The 178.97° dichoral angle occurs between the triangular prism in the front of the projection image, and the square pyramid on the front right.
Here are the coordinates:
- Code: Select all
set A = polyroot(<-47, 494, -1119, -1808, 2128, 13696, 6112, -39680, -25600, 35328, 26880>, 0.2, 0.22)
set B = √(1 - A^2)
set C = √(2*(1 - 2*A))
set D = √(3 - 4*A^2)
set E = √(1 + A)
set F = 2*(1 - A)
# The two J89 cells
<±1, ±1, 2*B, ±1>
<±1, ±(1+2*A), 0, ±1>
<±(1 + C/√(1-A)), 0, -(2*A^2 + A - 1)/B, ±1>
<0, ±1, -D, ±1>
<±(D*C + E)/(F*E), 0, (2*A-1)*D/F - C/(F*E), ±1>
# The augment
<0, 0, 2*B + 1, 0>
A is the root of the following polynomial between 0.20 and 0.22:
26880x10 + 35328x9 - 25600x8 - 39680x7 + 6112x6 + 13696x5 + 2128x4 - 1808x3 - 1119x2 + 494x - 47 = 0
Approximate value is A = 0.216844815713457.
Last edited by quickfur on Mon Feb 01, 2021 7:45 pm, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
I just looked through the 3D crown jewels (J84-J90) besides the EKF-related icosahedral ones, and it seems that J89 and J86 may be the only cases where their 4D prisms are augmentable! All the others have square faces with dihedral angles too shallow to fit a height-1/2 square pyramid, and triangular faces with dihedral angles too shallow to fit a tetrahedron of height √(5/2)/2 (height of a 5-cell). I haven't numerically verified this, but a quick visual scan of my projection images showed obvious shallow angles that wouldn't fit any augment.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
(You know, I have my own images which show the angles numerically: viewtopic.php?p=27561#p27561)
Here are some more polyhedra whose prisms are augmentable with cube pyramids: n-gon prism (n < 8), truncated octahedron, elongated pentagonal pyramid, triangular orthobicupola, square antiprism.
And isn't the snub dodecahedron prism also augmentable with pentagonal prism pyramids? (I get a dichoral angle of 152.93°+13.28°=166.21°.) This is significant because, like most of J84-90, it's not constructible; it requires cube roots.
Also consider bilbiro, thawro, and pocuro with pentagonal prism pyramids.
Here are some more polyhedra whose prisms are augmentable with cube pyramids: n-gon prism (n < 8), truncated octahedron, elongated pentagonal pyramid, triangular orthobicupola, square antiprism.
And isn't the snub dodecahedron prism also augmentable with pentagonal prism pyramids? (I get a dichoral angle of 152.93°+13.28°=166.21°.) This is significant because, like most of J84-90, it's not constructible; it requires cube roots.
Also consider bilbiro, thawro, and pocuro with pentagonal prism pyramids.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 565
- Joined: Tue Sep 18, 2018 4:10 am
Re: Augmented polyhedral prisms
Yeah I didn't consider J91 and J92 because I knew for sure they would have many augmentations, being EKF related polytopes which have historically shown huge numbers of CRF modifications.
I'm currently writing a program to automatically compute all prism augmentation candidates using a database of 3D CRFs that I've been building. I'm expecting that unless unexpected complications arise this should give us a total count of the number of such CRF augmented prisms. I'm expecting a large number to come from polyhedra with pentagonal faces, since the pentagonal prism pyramid is extremely shallow and can fit in many places.
I'm currently writing a program to automatically compute all prism augmentation candidates using a database of 3D CRFs that I've been building. I'm expecting that unless unexpected complications arise this should give us a total count of the number of such CRF augmented prisms. I'm expecting a large number to come from polyhedra with pentagonal faces, since the pentagonal prism pyramid is extremely shallow and can fit in many places.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
I cooked up the database this morning. Armed with dihedral angle information, here's the list of 3D CRFs for which their 4D prisms are augmentable with n-prism pyramids:
Tetrahedron, truncated tetrahedron, square antiprism, pentagonal antiprism, octahedron, cuboctahedron, truncated octahedron, cube, rhombicuboctahedron, icosidodecahedron, truncated icosahedron, dodecahedron, rhombicosidodecahedron, J1 (square pyramid), J10, J11, J16, J19, J2, J20, J21, J23, J24, J25, J27, J28, J29, J3, J30, J31, J32, J33, J34, J37, J38, J39, J4, J40, J41, J42, J43, J45, J46, J47, J48, J49, J5, J50, J52, J53, J54, J56, J58, J59, J6, J60, J61, J62, J63, J65, J66, J67, J68, J69, J7, J70, J71, J72, J73, J74, J75, J76, J77, J78, J79, J8, J80, J81, J82, J83, J86, J89, J9, J91, J92, triangular prism, pentagonal prism, hexagonal prism, heptagonal prism, octagonal prism, snub dodecahedron.
The criteria I used were:
- For triangles, the largest dihedral angle must be ≤ 114.094842552110691° (which is 180° - the dihedral angle of the triangular prism pyramid);
- For squares, the largest dihedral angle must be ≤ 135°;
- For pentagons, the largest dihedral angle must be ≤ 166.717474411461012° (which is 180° - the dihedral angle of the pentagonal prism pyramid, a very shallow angle! so lots of stuff qualifies).
Of particular interest are the polyhedra that contain square cupola segments; these have dihedral angles exactly equal to 135°, which means the 4D augment will have coplanar cells with the adjacent cubes (square prisms from the lateral square faces of the cupola), forming elongated square pyramid cells! These are:
Rhombicuboctahedron, J19, J23, J28, J29, J37, J4, J45, J66, J67, octagonal prism.
And just as I suspected, between J84 and J90 the only two augmentable cases are J86 and J89. Of course, J91 and J92 can be augmented with pentagonal prism pyramids, but that's hardly surprising considering how shallow the latter is; it can fit almost anywhere there's a pentagonal prism. We already know the dodecahedral prism is augmentable -- that's what started this whole thread
We already know the dodecahedral prism is augmentable -- that's what started this whole thread  -- and apparently the pentagonal prism pyramid is shallow enough to also accomodate the snub dodecahedral prism. Edit: in fact, the only polyhedron with pentagons that are not augmentable is J64 (augmented tridiminished icosahedron). Every other pentagon occurring in a 3D CRF is augmentable!
-- and apparently the pentagonal prism pyramid is shallow enough to also accomodate the snub dodecahedral prism. Edit: in fact, the only polyhedron with pentagons that are not augmentable is J64 (augmented tridiminished icosahedron). Every other pentagon occurring in a 3D CRF is augmentable!
There's more to this, though. So far we only considered n-prism pyramid augments; but it should be possible to augment, say, hexagonal prisms with 6p||triangle, i.e., the (partial) Stott expansions of the augments. We could expand the criteria to include hexagons, octagons, and decagons too, which would give us more augmentable 4D prisms.
Tetrahedron, truncated tetrahedron, square antiprism, pentagonal antiprism, octahedron, cuboctahedron, truncated octahedron, cube, rhombicuboctahedron, icosidodecahedron, truncated icosahedron, dodecahedron, rhombicosidodecahedron, J1 (square pyramid), J10, J11, J16, J19, J2, J20, J21, J23, J24, J25, J27, J28, J29, J3, J30, J31, J32, J33, J34, J37, J38, J39, J4, J40, J41, J42, J43, J45, J46, J47, J48, J49, J5, J50, J52, J53, J54, J56, J58, J59, J6, J60, J61, J62, J63, J65, J66, J67, J68, J69, J7, J70, J71, J72, J73, J74, J75, J76, J77, J78, J79, J8, J80, J81, J82, J83, J86, J89, J9, J91, J92, triangular prism, pentagonal prism, hexagonal prism, heptagonal prism, octagonal prism, snub dodecahedron.
The criteria I used were:
- For triangles, the largest dihedral angle must be ≤ 114.094842552110691° (which is 180° - the dihedral angle of the triangular prism pyramid);
- For squares, the largest dihedral angle must be ≤ 135°;
- For pentagons, the largest dihedral angle must be ≤ 166.717474411461012° (which is 180° - the dihedral angle of the pentagonal prism pyramid, a very shallow angle! so lots of stuff qualifies).
Of particular interest are the polyhedra that contain square cupola segments; these have dihedral angles exactly equal to 135°, which means the 4D augment will have coplanar cells with the adjacent cubes (square prisms from the lateral square faces of the cupola), forming elongated square pyramid cells! These are:
Rhombicuboctahedron, J19, J23, J28, J29, J37, J4, J45, J66, J67, octagonal prism.
And just as I suspected, between J84 and J90 the only two augmentable cases are J86 and J89. Of course, J91 and J92 can be augmented with pentagonal prism pyramids, but that's hardly surprising considering how shallow the latter is; it can fit almost anywhere there's a pentagonal prism.
 We already know the dodecahedral prism is augmentable -- that's what started this whole thread
We already know the dodecahedral prism is augmentable -- that's what started this whole thread  -- and apparently the pentagonal prism pyramid is shallow enough to also accomodate the snub dodecahedral prism. Edit: in fact, the only polyhedron with pentagons that are not augmentable is J64 (augmented tridiminished icosahedron). Every other pentagon occurring in a 3D CRF is augmentable!
-- and apparently the pentagonal prism pyramid is shallow enough to also accomodate the snub dodecahedral prism. Edit: in fact, the only polyhedron with pentagons that are not augmentable is J64 (augmented tridiminished icosahedron). Every other pentagon occurring in a 3D CRF is augmentable!There's more to this, though. So far we only considered n-prism pyramid augments; but it should be possible to augment, say, hexagonal prisms with 6p||triangle, i.e., the (partial) Stott expansions of the augments. We could expand the criteria to include hexagons, octagons, and decagons too, which would give us more augmentable 4D prisms.
Last edited by quickfur on Tue Feb 02, 2021 2:27 pm, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
OK, expanding the criteria to include hexagons/octagons/decagons with max dihedral angles 114.094842552110691°, 135°, 166.717474411461012° respectively, we get these additional augmentables:
Hexagons:
Truncated tetrahedron (both triangles and hexagons augmentable!), hexagonal antiprism, J18, J22, J3, hexagonal prism (both squares and hexagons augmentable).
Octagons:
Octagonal antiprism, truncated cube, great rhombicuboctahedron (x4x3x), J19, J23, J4, J66, octagonal prism.
Decagons:
Decagonal antiprism, truncated dodecahedron, great rhombicosidodecahedron (x5x3x), J20, J21, J24, J25, J5, J6, J68-J71, J76-J83, decagonal prism.
Some were already included in the previous list but repeated here because additional faces become augmentable under the expanded criteria.
Hexagons:
Truncated tetrahedron (both triangles and hexagons augmentable!), hexagonal antiprism, J18, J22, J3, hexagonal prism (both squares and hexagons augmentable).
Octagons:
Octagonal antiprism, truncated cube, great rhombicuboctahedron (x4x3x), J19, J23, J4, J66, octagonal prism.
Decagons:
Decagonal antiprism, truncated dodecahedron, great rhombicosidodecahedron (x5x3x), J20, J21, J24, J25, J5, J6, J68-J71, J76-J83, decagonal prism.
Some were already included in the previous list but repeated here because additional faces become augmentable under the expanded criteria.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
seems that username's find opened a box of pandorra!
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
Klitzing wrote:seems that username's find opened a box of pandorra!


The good thing is that it finally motivated me to finish up that database of 3D CRFs that I've been wanting to build for a long time, but just never got around to. It's a sqlite3 database containing 130 polyhedra: the platonic solids, archimedeans, johnsons (with chiral polyhedra having 2 entries each, one for each enantiomer), and a selected number of prisms and antiprisms (of degrees 3, 4, 5, 6, 7, 8, 10, 20, the last only the prism). There's a total of 3321 vertices, 6390 edges, and 3329 faces, and 38340 lattice entries (basically edges in the face lattices of the 130 polyhedra). It weighs in at a modest size of ~2.7MB, and with the help of a sqlite3 client, you can run all sorts of queries on it.
For example, the question of which polyhedra's 4D prisms can be augmented by n-prism pyramids and/or 2n-prism||n-gons is answered by this query:
- Code: Select all
select * from (
select p.name, f.id, f.degree, max(e.dihedral) m
from edge e, face f, lattice l, polyhedron p
where e.poly = p.id and f.poly=p.id and l.poly=p.id and
l.dim1=1 and l.id1=e.id and
l.dim2=2 and l.id2=f.id
group by p.id,f.id
order by p.id,f.id
)
where
(degree = 3 and m <= 114.094842552110691) or
(degree = 4 and m <= 135) or
(degree = 5 and m <= 166.717474411461012) or
(degree = 6 and m <= 114.094842552110691) or
(degree = 8 and m <= 135) or
(degree = 10 and m <= 166.717474411461012)
;
This returns a list of all the faces satisfying the given dihedral angle criteria, which tells you the exact face on which polyhedron corresponds with an augmentable cell in the corresponding 4D prism.
I'm currently writing a program that takes this data and constructs actual 4D models out of it. So far, the query returns 654 rows, but this is not an accurate count because (1) it does not take isomorphism under symmetry into account, so there's a bunch of redundant entries; and (2) it only accounts for single augmentations; in some cases multiple augments are certainly possible. Also, for the degree=6,8,10 cases the above query does not take into account the orientation of the augment, which may matter in some cases. And some augments have coplanar cells which need to be vetted whether they are valid CRF cells and not illegal cells like trigonal prism + cube = elongated triangular prism (non-CRF). Actually constructing the 4D models will help identify any invalid cases that may have slipped through.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
I finished the first version of the program that automatically constructs augmentations of prisms of 3D CRFs. It's mostly there, but not 100% yet -- still lacking a way to control the orientation of 2n-prism||n-gon augments (currently they are in arbitrary orientation). But from preliminary experimentation, I'm expecting a large number of such augmentations from the 2n-prism||n-gon augmentations, because for n=5, the augment is so shallow it pretty much can go anywhere on a polyhedron with pentagonal faces, and furthermore, it has 2 orientations, which significantly adds to the number of combinations.
For example, the truncated dodecahedron, the great rhombicosidodecahedron (and its various gyrations/truncations) all can have many combinations of augments, and adjacent augments are not a problem.
Also, even for n=4 the number of possibilities is quite high. For example, the truncated cube prism can take augments on any subset of its 8-prism cells, and each augment can have 2 orientations; the x4x3x prism also allow this. This along with analogous augmentations of various modifications like the augmented truncated cube prisms gives rise to a large number of combinations.
An exact count will need more careful analysis, but I'm expecting a combinatorial explosion of possibilties.
For example, the truncated dodecahedron, the great rhombicosidodecahedron (and its various gyrations/truncations) all can have many combinations of augments, and adjacent augments are not a problem.
Also, even for n=4 the number of possibilities is quite high. For example, the truncated cube prism can take augments on any subset of its 8-prism cells, and each augment can have 2 orientations; the x4x3x prism also allow this. This along with analogous augmentations of various modifications like the augmented truncated cube prisms gives rise to a large number of combinations.
An exact count will need more careful analysis, but I'm expecting a combinatorial explosion of possibilties.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
Won't be besides of the squappip + 2 cubpy blend also a squappip + 2 squappy blend too?
Could someone check the according dihedrals?
--- rk
Could someone check the according dihedrals?
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
Klitzing wrote:Won't be besides of the squappip + 2 cubpy blend also a squappip + 2 squappy blend too?
Could someone check the according dihedrals?
[...]
Output from my program:
- Code: Select all
$ aug_prisms show 20
[20] square antiprism:
[3] square (max 103.836°)
[4] square (max 103.836°)
$
So yes, squappip is augmentable by two cubpy's. The maximal dihedral angles around the square faces is 103.836°. Here's a render:
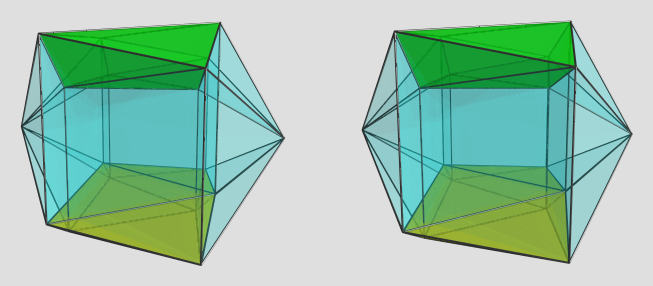
Green and yellow cells are square antiprisms (seen sideways), augments are on the left and right.
On a related note, here's an interesting observation: if some n-dimensional CRF polytope P has a facet F that can be augmented with an F-pyramid, but becomes concave because of too large a difacetal angle, it might be possible to augment P-prism with an (F-prism)-pyramid instead. Because in general, the (F-prism)-pyramid will have shallower difacetal angles that the F-pyramid itself.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
haha,
you showed up the squappip + 2 cubpy - blend again.
But I was refering to the squappip + 2 squappy - blend instead.
As the base angle of the squappy is arccos[sqrt(sqrt(2))/2] = 53.515624°,
that of cubpy is 45°, and the cube-squap dihedral in squappip is 90°,
all 4 augmentations cannot be applied simultanuously, when restricting to CRFs.
--- rk
you showed up the squappip + 2 cubpy - blend again.
- Code: Select all
o4o
x4o x4o -- x x4o (cube)
o4x o4x -- x o4x (gyro cube)
o4o
| |
| +-- s2s4s (squap)
+-------- s2s4s (squap)
But I was refering to the squappip + 2 squappy - blend instead.
- Code: Select all
x4o x4o -- x x4o (cube)
o4o o4o
o4x o4x -- x o4x (gyro cube)
| |
| +-- s2s4s (squap)
+-------- s2s4s (squap)
As the base angle of the squappy is arccos[sqrt(sqrt(2))/2] = 53.515624°,
that of cubpy is 45°, and the cube-squap dihedral in squappip is 90°,
all 4 augmentations cannot be applied simultanuously, when restricting to CRFs.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Augmented polyhedral prisms
Klitzing wrote:[...]squappip + 2 squappy - blend[...]
Ah, I see. Here's a crude render:
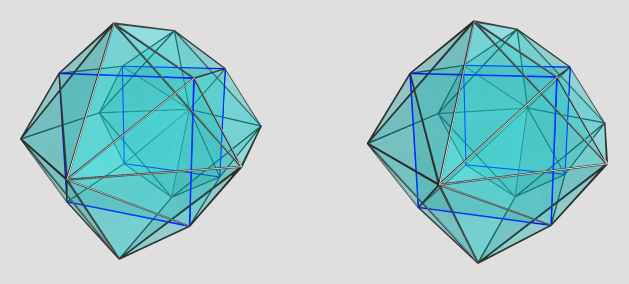
The blue lines show edges on the far side of the polytope. The square antiprisms are internal to the polytope; in their place are florets of 2 square pyramids joined by 8 tetrahedra. Cubes and triangular prisms connect the two ends.
As the base angle of the squappy is arccos[sqrt(sqrt(2))/2] = 53.515624°,
that of cubpy is 45°, and the cube-squap dihedral in squappip is 90°,
all 4 augmentations cannot be applied simultanuously, when restricting to CRFs.
Correct, these augments are not compatible with each other.
This does raise the interesting question of prisms of orbiform polyhedra of radius ≤ edge length, where one could erect pyramids on the base polyhedra in addition to the lateral augments my program calculated. There may be some cases where both types of augments can exist simultaneously; then that would lead to a large number of combinations.
In fact, J91 and J92 immediately come to mind: they are non-orbiform but we did discover pseudopyramids of them; given the shallow dichoral angles, I'd guess that both the pseudopyramid augments and the lateral 5-prism pyramid augments could exist simultaneously. So there ought to be quite a good number of combinations arising just from these. The J32 prism would also be amenable to this hybrid augmentation. There are probably others.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
Could 2n-prism || n-gon be called a pseudo-pyramid?
What is the reason for the term "magnabicupolic ring"? Why not just "bicupolic ring"?
What is the reason for the term "magnabicupolic ring"? Why not just "bicupolic ring"?
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 565
- Joined: Tue Sep 18, 2018 4:10 am
Re: Augmented polyhedral prisms
mr_e_man wrote:Could 2n-prism || n-gon be called a pseudo-pyramid?
What is the reason for the term "magnabicupolic ring"? Why not just "bicupolic ring"?
It's historical. An n-gonal bicupolic ring is the same as 2n-gon||n-prism, whereas a magnabicupolic ring is 2n-prism||n-gon.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
quickfur wrote:mr_e_man wrote:Could 2n-prism || n-gon be called a pseudo-pyramid?
What is the reason for the term "magnabicupolic ring"? Why not just "bicupolic ring"?
It's historical. An n-gonal bicupolic ring is the same as 2n-gon||n-prism, whereas a magnabicupolic ring is 2n-prism||n-gon.
2n-gon atop n-prism is orthobicupolic ring. There's also a gyrobicupolic ring that has an antiprism base instead.
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Augmented polyhedral prisms
Also, concerning pseudo-pyramids, we coined that term for pyramid-like constructions involving a base that isn't orbiform (circumscribed by an n-sphere). Things like 2n-prism||n-gon are really more Stott expansions of proper pyramids than anything else, so I'd reserve "pseudo-pyramid" only for when the base is not orbiform. Such as J91 pseudo-pyramid.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
I'm probably late to the party on this one, but could hexagonal/octagonal/decagonal prism cells of 3D-CRF prisms be augmented with triangular/square/pentagonal pucofastegia (K-4.51, 101, and 165, respectively)?
I don't even think I need to ask about antifastegia (K-4.6, 14, and 93, respectively), they don't look nearly shallow enough.
I don't even think I need to ask about antifastegia (K-4.6, 14, and 93, respectively), they don't look nearly shallow enough.
-

New Kid on the 4D analog of a Block - Dionian
- Posts: 26
- Joined: Mon Jul 16, 2018 2:27 am
- Location: Pacific Northwest
Re: Augmented polyhedral prisms
New Kid on the 4D analog of a Block wrote:I'm probably late to the party on this one, but could hexagonal/octagonal/decagonal prism cells of 3D-CRF prisms be augmented with triangular/square/pentagonal pucofastegia (K-4.51, 101, and 165, respectively)?
I don't even think I need to ask about antifastegia (K-4.6, 14, and 93, respectively), they don't look nearly shallow enough.
Of course they can, provided all the lateral dichoral angles are shallow enough to be convex or coplanar with the host prism's cells. In the latter case, certain coplanar cells are "prohibited" because they give rise to coplanar polygons, which become non-CRF (e.g., tetrahedron + octahedron). But other than that, yeah, sure they can.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Augmented polyhedral prisms
username5243 wrote:quickfur wrote:mr_e_man wrote:Could 2n-prism || n-gon be called a pseudo-pyramid?
What is the reason for the term "magnabicupolic ring"? Why not just "bicupolic ring"?
It's historical. An n-gonal bicupolic ring is the same as 2n-gon||n-prism, whereas a magnabicupolic ring is 2n-prism||n-gon.
2n-gon atop n-prism is orthobicupolic ring. There's also a gyrobicupolic ring that has an antiprism base instead.
I guess I found the source: viewtopic.php?p=16461#p16461, and the next page or so, in particular
Keiji wrote:As for the "reverse ortho" form, I like itPerhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".
(Make that "octagonal", not "octahedral".)
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 565
- Joined: Tue Sep 18, 2018 4:10 am
88 posts
• Page 3 of 3 • 1, 2, 3
Who is online
Users browsing this forum: No registered users and 53 guests
