
Marek's post about the bilunabirotunda (J91) inspired me to investigate possible CRF combinations of this shape. One of J91's interesting characteristics is that it contains a pentagon-triangle-pentagon-triangle combination with exactly the same dihedral angles as the icosidodecahedron o5x3o (probably this is why Johnson named it bilunabirotunda). For convenience of reference, lemme just borrow Wikipedia's J91 image here:

The most interesting thing about this part of J91 is that the angle between the two pentagons around their common vertex is exactly equal to the dihedral angle of the regular dodecahedron, or, equivalently, is the same as in the icosidodecahedron o5x3o. This fact gave me an idea: suppose we take three J91's and paste them together at their pentagonal faces, such that the three J91's share the vertex between two pentagons and two triangles. Since the pentagon-triangle-pentagon-triangle combination is just a section of o5x3o, the angle defect will be positive, which means we can then fold the J91's into 4D so that these pentagonal faces are joined to each other. The dichoral angles around this vertex, then, must be exactly the same as in the rectified 120-cell o5x3o3o. We can therefore insert tetrahedra to fill in the remaining gaps around this vertex, and the dichoral angles that the tetrahedra make around this vertex will be exactly the same as in o5x3o3o.
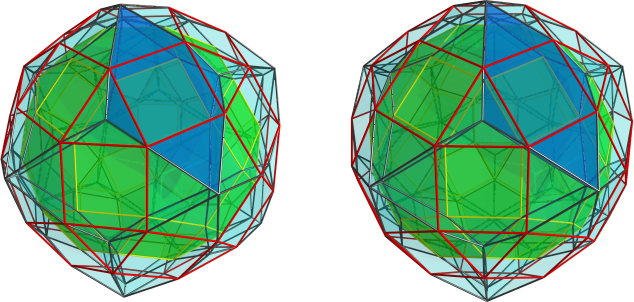
Now, take a look at this projection of o5x3o3o, showing its equatorial o5x3o cells:

Notice that where three o5x3o's meet, there's the outline of a tetrahedron? So the dichoral angles of the cells around this tetrahedron would match the dichoral angles of the J91's that we have folded together into 4D. Now notice that on the opposite side of the o5x3o's in the above image, we have an identical tetrahedral configuration of cells: so if we ignore the middle portion of the o5x3o, say if we mentally "collapse" the o5x3o's so that they form rhombus-shaped projection images above, then this should represent the configuration of J91's that we have thus assembled (because the dichoral angle around the 5.3.5.3 vertex in the J91 is the same as the dichoral angle of the vertices of the o5x3o). Therefore, it seems reasonable to deduce that if we continue attaching more J91's to our set of three in the same pattern, five J91's should close up into a pentagonal formation. This implies that the J91's edges between two pentagonal faces will be where five J91's will meet (these are the top and bottom edges in the Wikipedia image of J91). Therefore, we should be able to attach 30 J91's to each other and form a closed network with icosahedral symmetry. And since the top and bottom edges of the J91's will have 5 triangles around either end, we can insert pentagonal pyramids to fill up the gaps.
This then produces a pattern of faces with the configuration 3.4.5.4 around each vertex, in icosahedral symmetry, i.e., the faces of a x5o3x. Therefore, we should be able to sandwich our 30 J91's between two x5o3x's to form a closed 4D shape. If my deductions are correct, the result should be CRF, and would be a tetrastratic polychoron with two x5o3x's, 30 J91's, 12 pentagonal pyramids, and 20 tetrahedra.
Can someone verify whether this shape actually exists, and is CRF?

P.S. The lace tower of this polychoron should be x5o3x || o5o3A || B5o3o || o5o3A || x5o3x where A and B are as-yet unknown scalars. The height of the tower should be exactly the Golden Ratio (chord of the pentagonal faces of the J91's).



 Plus, I made several mistakes in my own partial calculations, so it's a good thing I can just reference yours when the numbers don't come out right.
Plus, I made several mistakes in my own partial calculations, so it's a good thing I can just reference yours when the numbers don't come out right. 

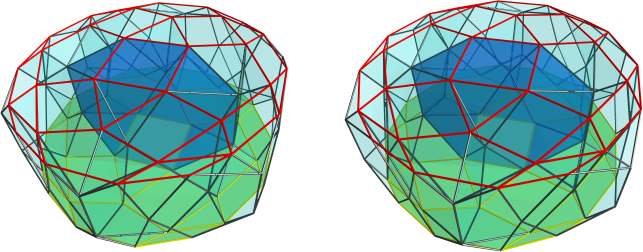

 )
)

 . I apologise for being so stubborn. the way I concluded It was impossible is by looking at the edge with the tetahedron and two bilunabirotunda's. This edge fixes the bichoral angle for the pentagon, and thus 5 is the only possibility
. I apologise for being so stubborn. the way I concluded It was impossible is by looking at the edge with the tetahedron and two bilunabirotunda's. This edge fixes the bichoral angle for the pentagon, and thus 5 is the only possibility  .
.