Johnsonian Polytopes
Re: Johnsonian Polytopes
Of course, it's not uniform - it has rhombic ridges. There was error in my angles computations. Actually, their sum is exactly 180°, so the resulting polytope has cells that are unions of 4- and 3-pyramids.
But it's the best that we could find on this way. Ok, let's look in other directions...
But it's the best that we could find on this way. Ok, let's look in other directions...
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:Of course, it's not uniform - it has rhombic ridges. There was error in my angles computations. Actually, their sum is exactly 180°, so the resulting polytope has cells that are unions of 4- and 3-pyramids.
But it's the best that we could find on this way. Ok, let's look in other directions...
I see.
I'm trying to derive coordinates for joining the square biantiprismic ring to itself by the square antiprism cell. One way of doing this leads to a non-convex polychoron, but the other way may yield a CRF. However, the coordinates are very ugly... the 2^(1/4) height of the square antiprism is making the algebra really unmanageable when I try to solve for uniform edge lengths.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:I see.
I'm trying to derive coordinates for joining the square biantiprismic ring to itself by the square antiprism cell. One way of doing this leads to a non-convex polychoron, but the other way may yield a CRF. However, the coordinates are very ugly... the 2^(1/4) height of the square antiprism is making the algebra really unmanageable when I try to solve for uniform edge lengths.
But it is what we've done just now!
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:quickfur wrote:I see.
I'm trying to derive coordinates for joining the square biantiprismic ring to itself by the square antiprism cell. One way of doing this leads to a non-convex polychoron, but the other way may yield a CRF. However, the coordinates are very ugly... the 2^(1/4) height of the square antiprism is making the algebra really unmanageable when I try to solve for uniform edge lengths.
But it is what we've done just now!
Argh, OK, i guess i totally misunderstood you. You're right, those coordinates are exactly what results when you join the two in this way. I got confused from trying to do too many things at once.

 Trying to do 4D geometry at the same time as work (and answering other forums) is not a good combination.
Trying to do 4D geometry at the same time as work (and answering other forums) is not a good combination. 
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Is there any estimates of the number of diminished 600-cells? Now we counted only two of them, but what about all others? Should we make a list of them, or just write total number?
And... what is the bihedral angle of dodecaheral pyramid? Are there any augmented 120-cells, and is there a limitation for sets of faces (can we add pyramids two connected faces or not). In the latter case number of augmented 120-cells is the same as of diminished 600-cells
And... what is the bihedral angle of dodecaheral pyramid? Are there any augmented 120-cells, and is there a limitation for sets of faces (can we add pyramids two connected faces or not). In the latter case number of augmented 120-cells is the same as of diminished 600-cells

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:Is there any estimates of the number of diminished 600-cells? Now we counted only two of them, but what about all others? Should we make a list of them, or just write total number?
OK, for the snub 24-cell diminishing, it's clear that all subsets of the 24 icosahedral pyramids will give a CRF diminishing of the 600-cell. The upper bound is 2^24 = 16777216, but because of symmetry, the real number will be significantly less than that. (I'm not sure how to count the exact number.) However, the number will be larger than if you account for symmetry, because you can remove icosahedral pyramids from the 600-cell with some pyramids not lying on the 24-cell of other removed pyramids.
For the grand antiprism diminishing, some subsets are possible but not others, but I'm not sure which are valid and which are not. At the very least, we know there's a "half grand antiprism", with only 1 ring of pentagonal antiprisms (by not removing the other ring of vertices). There may be other configurations as well, such as rings that are not orthogonal, where some antiprisms from one ring touches the other ring.
I don't know of any other diminishings of the 600-cell. At the equator it does have edges that form an icosidodecahedron in a hyperplane, but cutting the 600-cell in half also cuts some of the tetrahedra that sit across the equator (between the icosidodecahedron edges) so this doesn't give a CRF polychoron. I don't know if it's possible to retain those tetrahedra and insert other kinds of cells to close it up without rebuilding the entire 600-cell again. I doubt it will work.
And... what is the bihedral angle of dodecaheral pyramid? Are there any augmented 120-cells, and is there a limitation for sets of faces (can we add pyramids two connected faces or not). In the latter case number of augmented 120-cells is the same as of diminished 600-cells
According to Wikipedia, the radius of a dodecahedron's vertices is about 1.4 times its edge length. So no, you can't augment the 120-cell with pyramids.

I wonder about the dodecahedron-icosahedron antiprism, though. Do you think the icosahedron end might be narrower than the dodecahedron end? If so, we may be able to attach CRF polychora with a dodecahedron base to make various elongated forms of it.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Last edited by quickfur on Wed Nov 23, 2011 5:03 am, edited 1 time in total.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Actually, I just realized that the 600-cell has a lot more diminishings than I thought. For example, there may be some diminishings where two removed icosahedral pyramids overlap a little, but the resulting new facets are still CRF polyhedra (diminished icosahedra). If so, there will be quite a lot more diminishings than is obvious at first glance!
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
I have discovered another CRF polychoron (haven't rigorously confirmed yet, but 90% confidence), based on the observation that the icosahedron's vertices have a radius smaller than its edge length (as proven by the existence of the 600-cell), and the observation that the centroid of the dodecahedron's faces lie at a radius farther than its edge length. This means that given a fixed edge length, we can fit an icosahedron inside a dodecahedron completely. Now, displace the icosahedron in the 4th direction until the convex hull has equal edge lengths -- this is possible because it is simply the dodecahedron-icosahedron antiprism. But the icosahedron's shadow lies completely inside the dodecahedron. This means that we can now take two of these antiprisms and join them at their dodecahedral bases, and the result must be convex, and therefore CRF.
So we have 2 icosahedral facets, 100 tetrahedra, 24 pentagonal pyramids. (The 100 tetrahedra are divided into two copies of 20+30, the 20 corresponding to the icosahedron's faces, and the 30 to its edges.)
Furthermore, we can elongate this polychoron by inserting a dodecahedral prism in between, and we can add icosahedral pyramids to either or both ends. So it has elongated and augmented forms too.
What should we call this polychoron? Maybe icosahedral biantiprism?
So we have 2 icosahedral facets, 100 tetrahedra, 24 pentagonal pyramids. (The 100 tetrahedra are divided into two copies of 20+30, the 20 corresponding to the icosahedron's faces, and the 30 to its edges.)
Furthermore, we can elongate this polychoron by inserting a dodecahedral prism in between, and we can add icosahedral pyramids to either or both ends. So it has elongated and augmented forms too.
What should we call this polychoron? Maybe icosahedral biantiprism?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
So, we should remove dodecaheral pyramids and related polychorons from the list. It's very contrintuitive for me, but such is reality...
For diminished of 600-cell, we can select one vertex and remove one icosahedral pyramid. Then select another vertex that is not adjacent to the first and remove its pyramid... and even if they are adjacent, you get a polytope with two diminish-icosahedra cells??? We have to understand, what constraints are here. No 3 vertex in the single cell? Or something more strong? But it looks like we are very close to 2^120 CRFs!
For diminished of 600-cell, we can select one vertex and remove one icosahedral pyramid. Then select another vertex that is not adjacent to the first and remove its pyramid... and even if they are adjacent, you get a polytope with two diminish-icosahedra cells??? We have to understand, what constraints are here. No 3 vertex in the single cell? Or something more strong? But it looks like we are very close to 2^120 CRFs!
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:So, we should remove dodecaheral pyramids and related polychorons from the list. It's very contrintuitive for me, but such is reality...
Already done.
It's not too counterintuitive if you consider that the pentagonal pyramid (with equilateral triangles) is very shallow (the next member in the sequence, the hexagonal pyramid, is completely flat), so it's too low to meet up at the center of dodecahedron. You can, of course, make a pyramid of the dodecahedron, but it will not have equilateral triangles.
For diminished of 600-cell, we can select one vertex and remove one icosahedral pyramid. Then select another vertex that is not adjacent to the first and remove its pyramid... and even if they are adjacent, you get a polytope with two diminish-icosahedra cells??? We have to understand, what constraints are here. No 3 vertex in the single cell? Or something more strong? But it looks like we are very close to 2^120 CRFs!
Yeah, there are a lot of possibilties here!! But what about symmetry though? Won't that reduce the number somewhat? But I guess it won't significantly reduce it, because we don't have O(2^100) symmetries here!
I'm not sure exactly what the constraints are. Obviously, removing two adjacent vertices is permitted, as proven by the existence of the grand antiprism. You will end up with either two gyro-elongated pentagonal pyramids or two pentagonal pyramids and a pentagonal antiprism (not sure which one). Removing 3 or more adjacent vertices will be more restricted, because you may end up with facets similar to the snub 24-cell's vertex figure, which is non-CRF. If I'm not mistaken, you can remove anywhere from 1 to 10 vertices along a great circle, and the result will still be CRF. You may be able to get a CRF from all (or most) subsets of the 10 vertices as well.
Now if you factor in other arrangements like non-orthogonal great circles that are far apart enough they don't affect each other, you can have another ring of 10 vertices (or maybe even three rings? not sure) with the same number of possible combinations. So you will get 2^10*2^10 possibilities for each possible pair of rings. That's insanely many possibilities! Forget the augmented duoprisms, the number of 600-cell diminishings dwarf the other CRFs by a loooong shot!

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Already done.
Change 56 to 52
But what about symmetry though? Won't that reduce the number somewhat?
14400 elements in symmetry group including mirrored states. Only 14 bits of 120...
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Stepping away from all CRF polychora for a while, there is a related question: Which are all PRIMITIVE CRF polychora?
A primitive polychoron is one that cannot be decomposed into others. Once you have this list, you can make all remaining CRF polychora by just augmentation. For example, out of all uniform + johnson polyhedra, octahedron is not primitive since it decomposes into two square pyramids, icosahedron is not primitive, as it can be diminished, cuboctahedron can be split in two triangular cupolas, rhombicuboctahedron splits into octahedral prism + two square cupolae, icosidodecahedron splits into two pentagonal rotundas and rhombicosidodecahedron can be diminished in various ways. From Johnson solids, all the elongated and gyroelongated bodies, all dipyramids and bicupolae, gyrobifastigium, anything augmented (including augmented tridiminished icosahedron and augmented sphenocorona) and all forms of rhombicosidodecahedron except for parabidiminished and tridiminished are non-primitive. So the list gets cut down quite a lot.
On the other hand, some augmented analogues seem possible for non-regular uniform polychora. Is it possible, for example, to augment truncated-tetrahedral cells of truncated pentachoron with truncated tetrahedron-tetrahedron copula? Augment truncated cubes in truncated tesseract with truncated cube-cube cupolas?
And for uniform shape that includes decagonal prisms, maybe capping them with pentagonal prism||decagonal prism, and then saddint a pentagonal prism pyramid atop that?
I don't know the dichoral angles, so I'm not sure which of these are possible, but augmented uniforms seem to be a large possible group.
Edit: and rectified 600-cell. It's made of octahedra and icosahedra, I feel that there is a possibility of many diminished shapes containing square pyramids and various types of diminished icosahedra.
Edit2: what I'm really interested in are 4D analogues of the "hard" Johnson shapes at the end of the list which don't require any uniform polyhedron to construct. Hereby, I suggest to call any such polychoron to be found a "crown jewel".
A primitive polychoron is one that cannot be decomposed into others. Once you have this list, you can make all remaining CRF polychora by just augmentation. For example, out of all uniform + johnson polyhedra, octahedron is not primitive since it decomposes into two square pyramids, icosahedron is not primitive, as it can be diminished, cuboctahedron can be split in two triangular cupolas, rhombicuboctahedron splits into octahedral prism + two square cupolae, icosidodecahedron splits into two pentagonal rotundas and rhombicosidodecahedron can be diminished in various ways. From Johnson solids, all the elongated and gyroelongated bodies, all dipyramids and bicupolae, gyrobifastigium, anything augmented (including augmented tridiminished icosahedron and augmented sphenocorona) and all forms of rhombicosidodecahedron except for parabidiminished and tridiminished are non-primitive. So the list gets cut down quite a lot.
On the other hand, some augmented analogues seem possible for non-regular uniform polychora. Is it possible, for example, to augment truncated-tetrahedral cells of truncated pentachoron with truncated tetrahedron-tetrahedron copula? Augment truncated cubes in truncated tesseract with truncated cube-cube cupolas?
And for uniform shape that includes decagonal prisms, maybe capping them with pentagonal prism||decagonal prism, and then saddint a pentagonal prism pyramid atop that?
I don't know the dichoral angles, so I'm not sure which of these are possible, but augmented uniforms seem to be a large possible group.
Edit: and rectified 600-cell. It's made of octahedra and icosahedra, I feel that there is a possibility of many diminished shapes containing square pyramids and various types of diminished icosahedra.
Edit2: what I'm really interested in are 4D analogues of the "hard" Johnson shapes at the end of the list which don't require any uniform polyhedron to construct. Hereby, I suggest to call any such polychoron to be found a "crown jewel".
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:Stepping away from all CRF polychora for a while, there is a related question: Which are all PRIMITIVE CRF polychora?
A primitive polychoron is one that cannot be decomposed into others. Once you have this list, you can make all remaining CRF polychora by just augmentation. For example, out of all uniform + johnson polyhedra, octahedron is not primitive since it decomposes into two square pyramids, icosahedron is not primitive, as it can be diminished, cuboctahedron can be split in two triangular cupolas, rhombicuboctahedron splits into octahedral prism + two square cupolae, icosidodecahedron splits into two pentagonal rotundas and rhombicosidodecahedron can be diminished in various ways. From Johnson solids, all the elongated and gyroelongated bodies, all dipyramids and bicupolae, gyrobifastigium, anything augmented (including augmented tridiminished icosahedron and augmented sphenocorona) and all forms of rhombicosidodecahedron except for parabidiminished and tridiminished are non-primitive. So the list gets cut down quite a lot.
That is what I mentioned it this post: viewtopic.php?p=16570#p16570 But there is additional difficulty: some kinds of diminishing in 4D lead to cutting of the original cell. Examples are 24-cell (you get square pyramids instead of octahedra) and diminished 600-cell (for some vertices we get diminished icosahedron as a part of old cell). So when you restore the body by augmenting you must be careful when sum of dichoral angles for some ridge is 180: don't drop this case away, but check, may be on other side there is augmentable polyhdedron.
Another thing is what kinds of augmention/diminishing are allowed. I see three ways:
A. we can cut off only pyramids. So we select a vertex with only triangular ridges in it - and we can use it for the diminishing. When we restore the body, we check all cells that have one of 13 pyramidable forms.
B. we can use any bodies (pyramids, cupola and may be something else) that have cells for which all dichoral angles are less that 90. Add list of such cells/bodies in the list of diminishing/augmention operations - but it will be more difficult to look for candidates for diminishing.
C. we can split any body when we see 3D section that doesn't cut any ridge. It's even more difficult to search such cuttings (or may be not? Loop for all vertices, then loop for all triads on adjacent vertices, build hyperplane and check that it does't intersect any ridge)... For the restoration process we have to check all pairs of bodies that have equal cells and check angles for combinations. We need to do it with the currect list of CRF anyway - but say to user "here is a list of primitives - now combine them in all possible ways yourself" is too cruel.
Anyway, the complete list of primitive CRFs may be very long again. It will include all ultimately diminished 600-cells (where we can't cut off any single vertex) and I don't see why there will be less than, say, 2^60 forms.
On the other hand, some augmented analogues seem possible for non-regular uniform polychora. Is it possible, for example, to augment truncated-tetrahedral cells of truncated pentachoron with truncated tetrahedron-tetrahedron copula? Augment truncated cubes in truncated tesseract with truncated cube-cube cupolas?
More candidates for way B

And for uniform shape that includes decagonal prisms, maybe capping them with pentagonal prism||decagonal prism, and then saddint a pentagonal prism pyramid atop that?
I don't know the dichoral angles, so I'm not sure which of these are possible, but augmented uniforms seem to be a large possible group.
For runcitruncated and omnitruncated 120-cell you probably will not get good result: these cupolas are what had been cut off on the way from runcinated 120-cell. But for {10,n} duoprisms there may be another rich family of augmented and double-augmented bodies

Edit: and rectified 600-cell. It's made of octahedra and icosahedra, I feel that there is a possibility of many diminished shapes containing square pyramids and various types of diminished icosahedra.
...and pentagonal prisms. Wow, it's more tasty than diminishing of 600-cell itself

Edit2: what I'm really interested in are 4D analogues of the "hard" Johnson shapes at the end of the list which don't require any uniform polyhedron to construct. Hereby, I suggest to call any such polychoron to be found a "crown jewel".
You mean it has no uniform cells? Take cubic bipyramid. But if it should be primitive... Ok, let's think about it.
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Marek14 wrote:Stepping away from all CRF polychora for a while, there is a related question: Which are all PRIMITIVE CRF polychora?
A primitive polychoron is one that cannot be decomposed into others. Once you have this list, you can make all remaining CRF polychora by just augmentation.
For the 600-cell, it's unclear at this time what is the most primitive diminishing. I'm not 100% sure, but I believe even the snub 24-cell can be further diminished to non-uniforms with diminished icosahedral cells. And there must be a huge number of other possibilities, even just with primitive diminished 600-cells alone.
But even after you find the primitive set, you still have the problem of what augmentations are possible, because some augmentations don't lead to convex results, so you will still need to manually enumerate the possibilities.
[...] On the other hand, some augmented analogues seem possible for non-regular uniform polychora. Is it possible, for example, to augment truncated-tetrahedral cells of truncated pentachoron with truncated tetrahedron-tetrahedron copula?
This may be possible, we'll have to investigate.
Augment truncated cubes in truncated tesseract with truncated cube-cube cupolas?
Now here's an interesting one. Is there a CRF cube-truncated cube cupola? If it does, this augmentation may be possible. I'll have to check.
And for uniform shape that includes decagonal prisms, maybe capping them with pentagonal prism||decagonal prism, and then saddint a pentagonal prism pyramid atop that?
Unfortunately you can't do that unless the dihedral angle of the decagonal prism with neighbouring cells is >= 90°, otherwise you get a non-convex polychoron. So the possibilities are quite limited.
I don't know the dichoral angles, so I'm not sure which of these are possible, but augmented uniforms seem to be a large possible group.
You may be right; I'm not sure if pentagonal pyramid capped truncated/rectified 600-cell is convex. If it is, you have another O(2^120) possible augmentations of each of these polytopes. Whoa, the 600-cell family is insanely huge in terms of generating CRFs!
Edit: and rectified 600-cell. It's made of octahedra and icosahedra, I feel that there is a possibility of many diminished shapes containing square pyramids and various types of diminished icosahedra.
Well, vertex figure is pentagonal prism. Not sure if it's uniform pentagonal prism? If so, you can generate lots of diminishings by cutting off vertices to get diminished icosahedral cells and pentagonal prisms.
Edit2: what I'm really interested in are 4D analogues of the "hard" Johnson shapes at the end of the list which don't require any uniform polyhedron to construct. Hereby, I suggest to call any such polychoron to be found a "crown jewel".
OK, maybe we should categorize the CRFs into those generated by uniform polychora and those that aren't?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
by Mrrl » Wed Nov 23, 2011 7:12 pm
by quickfur » Wed Nov 23, 2011 7:13 pm
Good timing

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
By "crown jewels" I mean things like triangular hebesphenorotunda. I don't see any simple way to finding this polyhedron if you start from uniforms. It exists, but it has no obvious relations to other uniforms or even Johnsons.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:By "crown jewels" I mean things like triangular hebesphenorotunda. I don't see any simple way to finding this polyhedron if you start from uniforms. It exists, but it has no obvious relations to other uniforms or even Johnsons.
So basically we have to pick three random Johnson solids with compatible faces, stick them together around a vertex, check if they have dihedral angle < 180°, then try all combinations of other solids to see if we can build a closed 4D shape out of it?
I think I'll start with more obvious combinations first, and then work my way to the more obscure ones. I consider it preliminary practice in building 4D shapes before the "real task" of building hard-to-guess CRFs.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Marek14 wrote:By "crown jewels" I mean things like triangular hebesphenorotunda. I don't see any simple way to finding this polyhedron if you start from uniforms. It exists, but it has no obvious relations to other uniforms or even Johnsons.
So basically we have to pick three random Johnson solids with compatible faces, stick them together around a vertex, check if they have dihedral angle < 180°, then try all combinations of other solids to see if we can build a closed 4D shape out of it?
I think I'll start with more obvious combinations first, and then work my way to the more obscure ones. I consider it preliminary practice in building 4D shapes before the "real task" of building hard-to-guess CRFs.
Yup, that;'s exactly why I call them "crown jewels"
 They are precious and hard to obtain.
They are precious and hard to obtain.I'd start with this: since augmentations of polytopes will be basically done by segmentochora, what are all segmentochora combinations that can be "chained" to form convex towers? (And still be used to augment other polytopes, obviously).
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:[...] I'd start with this: since augmentations of polytopes will be basically done by segmentochora, what are all segmentochora combinations that can be "chained" to form convex towers? (And still be used to augment other polytopes, obviously).
Well, the icosahedron-dodecahedron antiprism is one such segmentochoron (it's a segmentochoron 'cos it's essentially an icosahedron and a dodecahedron on two parallel hyperplanes with regular ridges between them), that i've already written about. Because the dodecahedron is larger than the icosahedron of the same edge length, you can join two of them by their dodecahedral base to make a convex polytope. And here's a render of it:
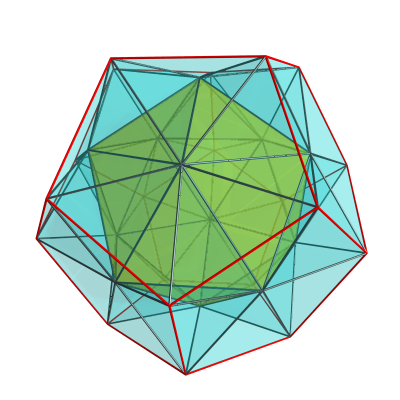
The red outlined dodecahedron is not a cell; it's the mid cross section (where the two original dodecahedra are). Now, the model I'm using is actually the joined biantiprism, but because the other half is hidden from view, this same image can also represent the original icosahedron/dodecahedron antiprism, in which case the red outlined dodecahedron is a cell.
 However, the side view will be different:
However, the side view will be different: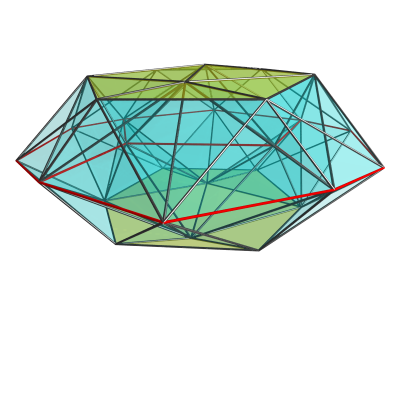
So you can see the biantiprism here, capped by two icosahedra, and some pyramids and tetrahedra linking them to the dodecahedral mid cross section. (Since I'm using perspective projection, the icosahedra actually lie on the far side of the projection, but you can see bits of yellow where the pyramids connect to them.)
As should be obvious from this projection, you can insert a dodecahedral prism in between to make the elongated biantiprism, and you can cap either or both ends with icosahedral pyramids. So from this base shape you can make two augmented forms, an elongated form, and two augmented elongated forms.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
So, to the rectified 600-cell. We see that a vertex of this object is a middle of edge of 600-cell. We can diminish rectified 600-cell by removing some subset of vertices if there is no any pair of corresponding edges of 600-cell belongs to the same ridge. So if we select large enough set of 600-cell edges keeping this property (every ridge contains zero or one edge from the set), we can select any subset of it, and get almost unique copy of the diminished rectified 600-cell.
The best result I got till now is 170 edges. It's a strange construction based on the grand antiprism:
you take 20 edges on antiprisms' axes (they are edges of 600-cell),
add to them 10 "parallels" of one tube (sides of pentagons) - 50 edges
then add 5 zig-zagged lines going along meridians of another tube - 50 more edges
and finally find 50 edges connecting tubes that don't belong to any ridge containig already selected edges.
170 in total
So now number of CRFs in finite families exceeds 2170/14400 An I think that there are much more others!
An I think that there are much more others!
The best result I got till now is 170 edges. It's a strange construction based on the grand antiprism:
you take 20 edges on antiprisms' axes (they are edges of 600-cell),
add to them 10 "parallels" of one tube (sides of pentagons) - 50 edges
then add 5 zig-zagged lines going along meridians of another tube - 50 more edges
and finally find 50 edges connecting tubes that don't belong to any ridge containig already selected edges.
170 in total

So now number of CRFs in finite families exceeds 2170/14400
 An I think that there are much more others!
An I think that there are much more others!Last edited by Mrrl on Wed Nov 23, 2011 9:01 pm, edited 1 time in total.
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
quickfur wrote:As should be obvious from this projection, you can insert a dodecahedral prism in between to make the elongated biantiprism, and you can cap either or both ends with icosahedral pyramids. So from this base shape you can make two augmented forms, an elongated form, and two augmented elongated forms.
However, the biantiprismal form definitely can't be used to augment anything uniform. Neither the elongated form. So the question is whether the side angles are shallow enough to augment a 120-cell or runcinated 120-cell (only uniform polychora that feature dodecahedra) with this, since if they are, then each augment can be, on top of that, capped with icosahedral pyramid.
My gut tells me that 120-cell is too round for this sort of augmentation. Not sure about runcinated 120-cell. Are there other shapes that can be put into segmentochoric relationship with dodecahedron? How about a cube...?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Mrrl wrote:[...]
So now number of CRFs in finite families exceeds 2170/14400An I think that there are much more others!
Wow, that's crazy. I think the 600-cell family deserves a category of their own, they generate so many CRFs! They are finite but really really numerous.
On another note, I've discovered another small family of CRFs related to the cupolae. Remember how you can make a 4D cube cupola by sweeping out a 4D bulk while you pull its faces apart? Well, you can also sweep out a 4D bulk by starting from a cube and pulling its edges apart. So you start with a cube and end with a truncated cube. The square faces turn into octahedra, so you generate 6 square cupola cells. The vertices generate 8 tetrahedra.
You can do the same thing for the tetrahedron, octahedron, icosahedron, dodecahedron. But here's the insight: all 3D uniform polyhedra except for prisms, antiprisms and the snubs, can be created from smaller versions by expanding faces or edges. For example, you can start with cuboctahedron and end with truncated cube (expand triangular faces) or truncated octahedron (expand square faces). You can start with truncated cube to get great rhombicuboctahedron (expand octagonal faces). Basically, given any ringings of the Coxeter-Dynkin diagram, if there are unringed nodes, then you can generate a cupola of it by expanding the element corresponding to the unringed node, this equals to adding a ring to that node.
So polyhedra with two unringed nodes will generate two kinds of cupola, and polyhedra with one unringed node will generate one cupola. Omnitruncates won't generate anything, obviously, since expanding any element will make it non-CRF.
The only thing is, I'm not 100% sure all of these constructions are CRF; there may be some combinations that will have unequal edge lengths. So this is only a tentative result. But it looks promising.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Marek14 wrote:[...] So the question is whether the side angles are shallow enough to augment a 120-cell or runcinated 120-cell (only uniform polychora that feature dodecahedra) with this, since if they are, then each augment can be, on top of that, capped with icosahedral pyramid.
My gut tells me that 120-cell is too round for this sort of augmentation. Not sure about runcinated 120-cell. Are there other shapes that can be put into segmentochoric relationship with dodecahedron? How about a cube...?
The runcinated 120-cell is even more round than the 120-cell, so if it doesn't work on the 120-cell, there's no hope for the runcinated 120-cell.

As for cube-dodecahedron segmentotope, I'm not 100% sure but I think you will get trapezoidal ridges from the cube to the larger cube inscribed in the dodecahedron so it won't be CRF. Also, the inscribed cube has a different edge length from the dodecahedron so you can't start with that either.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Bichoral angle of 120-cell is 144 deg (there exists ring of 10 dodecahedra connected by the opposite faces). Projection of icosahedron vertex in antiprism is too close to dodecahedron face, so 5-pyramid should be almost vertical. Probably there is nothing other than prism (and another antiprism), that has dodecahedral cell and may be augmented by the antiprism 

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
I've discovered another CRF candidate with square antiprism cells: start with a cube and truncate its vertices until it becomes a cuboctahedron, dragging it across the 4th direction to sweep out a 4D bulk. This produces a segmentochoron with 6 square antiprisms, 1 cube, 1 cuboctahedron, and 8 tetrahedra. Now this construction doesn't actually give you a CRF because the edge length of the cube and cuboctahedron are not equal. However, the cube cell can be scaled so that its edge length is equal to the cuboctahedron's edge length. Furthermore, because of vertex transitivity in all intermediate forms, all edges in the segmentochoron are transitive, so we can adjust the distance between the two cells to make all edge lengths equal. Then it will be a CRF polychoron.
Can someone confirm this?
As you may have guessed, this is part of a larger pattern that I'm investigating. Some members of this series have wide bases and narrow tops: they are candidates for augmenting other uniform polychora.
Can someone confirm this?

As you may have guessed, this is part of a larger pattern that I'm investigating. Some members of this series have wide bases and narrow tops: they are candidates for augmenting other uniform polychora.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Can someone confirm this?
Probably, your program can:
(±1,±1,±1,sqrt(4*sqrt(2)-3))
(±sqrt(2),±sqrt(2),0,0)
(±sqrt(2),0,±sqrt(2),0)
(0,±sqrt(2),±sqrt(2),0)
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
List of cells of 170-diminished rectified 600-cell:
170 pentagonal prisms;
350 square pyramids;
20 pentagonal antiprisms;
100 tridiminished icosahdera.
No icosahedra or octahedra survived
170 pentagonal prisms;
350 square pyramids;
20 pentagonal antiprisms;
100 tridiminished icosahdera.
No icosahedra or octahedra survived

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:quickfur wrote:Can someone confirm this?
Probably, your program can:
(±1,±1,±1,sqrt(4*sqrt(2)-3))
(±sqrt(2),±sqrt(2),0,0)
(±sqrt(2),0,±sqrt(2),0)
(0,±sqrt(2),±sqrt(2),0)
And six more vertices:
(±sqrt(2),0,0,-sqrt(2))
(0,±sqrt(2),0,-sqrt(2))
(0,0,±sqrt(2),-sqrt(2))
- just for fun

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
Mrrl wrote:[...]
(±1,±1,±1,sqrt(4*sqrt(2)-3))
(±sqrt(2),±sqrt(2),0,0)
(±sqrt(2),0,±sqrt(2),0)
(0,±sqrt(2),±sqrt(2),0)
Thanks so much!! Yes, it's confirmed. All edge lengths are equal, and there are 6 square antiprisms, 1 cube and 1 cuboctahedron. Here's an image:

The green is the cuboctahedral cell, the yellow is one of the 6 square antiprisms. You can see the cube outlined near the top of the image (as a flat frustum).
Even better, it looks like the cube's shadow completely falls inside the cuboctahedron, so it should be possible to make a bicupola from it, an elongate, and an augment with square pyramid, etc.. And also use it to augment tesseract truncates that have cuboctahedral cells!
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Who is online
Users browsing this forum: No registered users and 48 guests
