Johnsonian Polytopes
Re: Johnsonian Polytopes
Well, in cases where the chopped off caps at most touch, the cap clearly might be re-attached in a gyrated way (if at all possible, cf. below). But surely not if those intersect, what they do here.
Further there then has to be checked additional, whether the dihedral angles at those (re-)connections still are convex, else they disqualify as CRF.
Finally, in order to have at all the possibility of a gyration, the sectioning facet polytope should have a higher symmetry than that of the corresponding axis! Within the Johnsonians this is achieved rather easily: the axis is 3-, 4-, or 5-fold, but the base of the corresponding cupolae (or rotunda) are hexagons, octagons, resp. decagons. For polychora this is much harder. We have axes with tetrahedral, octahedral, or icosahedral symmetry. Thus the only sectioning facet polyhedra with a similar higher symmetry are o3x3o (octahedron within a tetrahedral context), x3o3x (cuboctahedron within a tetrahedral context), and x3x3x (truncated octahedron within a tetrahedral context). That is, we have to look for such polychora where some segmentochoral cap can be chopped off, which uses right these polyhedra for there bottom base and have tetrahedral axial symmetry.
Brique symmetry might look also be possible, but there clearly is just one non-degenerate bottom base which has higher symmetry: x2x2x (cube). But note that such an axis would occure only within (degenerate) 2,P-duoprisms, i.e. either x2x2xPo = x4o2xPo or x2x2xPx = x4o2x2Po.
(Suppose that's all. At least I don't see any further such subsymmetry right now.)
Thus the chosen segmentochora seem to be restricted to one of the followings: tet||oct, tet||co, tut||toe, {4}||cube, or line||cube, which then shall occur as caps at the corresponding axes. (Oct||co e.g. disqualifies because the top base likewise has the higher symmetry. And tut||co disqualifies too, as tut has the larger circumradius and thus co is not the bottom base, which has to be incident to the cut.)
--- rk
Further there then has to be checked additional, whether the dihedral angles at those (re-)connections still are convex, else they disqualify as CRF.
Finally, in order to have at all the possibility of a gyration, the sectioning facet polytope should have a higher symmetry than that of the corresponding axis! Within the Johnsonians this is achieved rather easily: the axis is 3-, 4-, or 5-fold, but the base of the corresponding cupolae (or rotunda) are hexagons, octagons, resp. decagons. For polychora this is much harder. We have axes with tetrahedral, octahedral, or icosahedral symmetry. Thus the only sectioning facet polyhedra with a similar higher symmetry are o3x3o (octahedron within a tetrahedral context), x3o3x (cuboctahedron within a tetrahedral context), and x3x3x (truncated octahedron within a tetrahedral context). That is, we have to look for such polychora where some segmentochoral cap can be chopped off, which uses right these polyhedra for there bottom base and have tetrahedral axial symmetry.
Brique symmetry might look also be possible, but there clearly is just one non-degenerate bottom base which has higher symmetry: x2x2x (cube). But note that such an axis would occure only within (degenerate) 2,P-duoprisms, i.e. either x2x2xPo = x4o2xPo or x2x2xPx = x4o2x2Po.
(Suppose that's all. At least I don't see any further such subsymmetry right now.)
Thus the chosen segmentochora seem to be restricted to one of the followings: tet||oct, tet||co, tut||toe, {4}||cube, or line||cube, which then shall occur as caps at the corresponding axes. (Oct||co e.g. disqualifies because the top base likewise has the higher symmetry. And tut||co disqualifies too, as tut has the larger circumradius and thus co is not the bottom base, which has to be incident to the cut.)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:Well, in cases where the chopped off caps at most touch, the cap clearly might be re-attached in a gyrated way (if at all possible, cf. below). But surely not if those intersect, what they do here.
Further there then has to be checked additional, whether the dihedral angles at those (re-)connections still are convex, else they disqualify as CRF.
Sorry, I didn't make myself clear again. I didn't mean gyration as cutting off a segmentochoron and reattaching it in rotated orientation; what I meant was, when we pick the two rings of icosahedra to diminish, one of the rings can be rotated relative to the other. That is, since there are 10 icosahedra in each orthogonal ring, and the bistratic diminishing is CRF only when we skip over every other icosahedron, we can only pick 5 icosahedra from each ring. So there are at least two ways to pick them: we can pick all the odd-numbered ones from the first ring and the even-numbered ones from the second ring, or we can pick odd-numbered ones from both rings. The case where both are even-numbered seems to be identical to the case where both are odd-numbered, due to duoprism rotational symmetry; what I haven't verified yet is whether picking odd+even vs. odd+odd is the same or not.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Klitzing wrote:Well, in cases where the chopped off caps at most touch, the cap clearly might be re-attached in a gyrated way (if at all possible, cf. below). But surely not if those intersect, what they do here.
Further there then has to be checked additional, whether the dihedral angles at those (re-)connections still are convex, else they disqualify as CRF.
Sorry, I didn't make myself clear again. I didn't mean gyration as cutting off a segmentochoron and reattaching it in rotated orientation; what I meant was, when we pick the two rings of icosahedra to diminish, one of the rings can be rotated relative to the other. That is, since there are 10 icosahedra in each orthogonal ring, and the bistratic diminishing is CRF only when we skip over every other icosahedron, we can only pick 5 icosahedra from each ring. So there are at least two ways to pick them: we can pick all the odd-numbered ones from the first ring and the even-numbered ones from the second ring, or we can pick odd-numbered ones from both rings. The case where both are even-numbered seems to be identical to the case where both are odd-numbered, due to duoprism rotational symmetry; what I haven't verified yet is whether picking odd+even vs. odd+odd is the same or not.
I think odd-odd is not the same as odd-even: first note that odd-even is the mirror-image of odd-odd. Now you can rotate the bicyclodiminished thingy over the plane in which the centers of one set of J80's lay over 180 degrees. Now one pentagon of centers is turned over a line (in a 3D-fashion), and the other one over a point (in a 2D-fashion). the J80's that are turned over a line look like they're mirrored, but the ones that are turned over a point are not mirrored, and thus odd-even is not the same as odd-odd.
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
I just constructed the version of the bicyclopentadiminished o5oxo where one ring is rotated relative to the other; so far, the cell counts appear to be identical, so it seems that at least in terms of surtopes, they are the same. But they may still be mirror-images of each other; I haven't eliminated that possibility yet.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
I have discovered another CRF diminishing of the o5oxo: a "meta"-bathodiminishing. This is produced by two deep cuttings of the o5oxo, each of which truncates it up to a truncated dodecahedron cross-section. Unlike the previous "meatball sandwich" cutting I posted earlier, though, in which the two cutting hyperplanes are parallel, in this one the hyperplanes make an angle of 72°. It just so happens that the two resulting truncated dodecahedra meet at a decagonal face, thus producing a peculiar spindle-like wedge structure with 31 icosahedra, 2 truncated dodecahedra, 22 pentagonal cupola, 120 octahedra, 12 pentagonal pyramids, and some other cells (I haven't counted them all yet), for a total of 287 cells. The pentagonal cupola wrap around the decagonal face between the two truncated dodecahedra, and are rimmed by a ring of 10 icosahedra around them.
Anyway, gotta run now, will post pictures later. This is a really fascinating discovery, because it doesn't have any analogue with any of the previous 120-cell family diminishings that we have found. I don't even know how to name this shape; it's not a luna because the decagonal "joint" where the two cutting hyperplanes meet is off-center, whereas the lunae we found before meet at the center. The o5oxo may be the only shape that admits a CRF result with this kind of strange cutting.
Update: Here's a render centered on the icosahedron (shown in red) antipodal to the decagon joining the two truncated dodecahedra:

The region surrounding the red icosahedron has basically the same structure as the original o5oxo, but it's pretty close to some areas of interest. In particular, two pentagonal pyramids (remains of two icosahedral cells that got truncated by the cutting hyperplanes), shown here in cyan outline, shares a vertex with it. The base of these pentagonal pyramids connect to a pentagonal cupola, the decagonal face of which (shown here in red outline) then interfaces with a truncated dodecahedron on the far side of the polytope (shown in next image). Square pyramids (bisected octahedra) interface this cupola to the intact remnants of the o5oxo. For clarity's sake, I've omitted the other cells visible from this viewpoint.
The next image shows the view from the opposite viewpoint, that is, centered on the decagon joining the two truncated dodecahedra, antipodal to the red icosahedron:
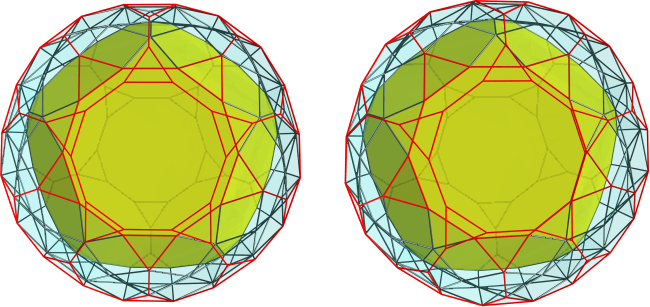
For the sake of clarity, one of the truncated dodecahedra is rendered in yellow, whereas the other one is outlined in red. The decagons opposite the central decagon between the two cells are where the pentagonal cupolae from the first picture connect to these cells. If you can do cross-eyed viewing, you can see outlines of pentagonal cupola wrapping in an alternating pattern all around the central decagon, filling in the gaps between these two truncated dodecahedra which meet at a rather acute angle.
This particular 3D viewpoint gives a false sense of volume due to familiar shapes like truncated dodecahedra, so here's the same projection (same 4D viewpoint) from a different 3D viewpoint, to show how narrow it is, that is, the truncated dodecahedra are being seen from quite a sharp angle.
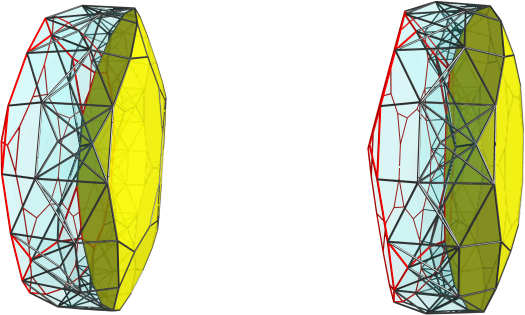
Since it's past bedtime, I don't have time to show more of the structure of that complex band wrapping around the two truncated dodecahedra, but you can sorta discern that it's an alternating pattern of pentagonal cupolae. There's also a ring of 10 icosahedra that wrap around this band, outside the ring of alternating pentagonal cupolae, not shown in any of these images, because they lie on what's left of the o5oxo's equator: since we're using 4D perspective projection, they're always just barely behind the limb of the projections so we can't see them directly.
Anyway, here are the coordinates of this odd little polychoron:
Anyway, gotta run now, will post pictures later. This is a really fascinating discovery, because it doesn't have any analogue with any of the previous 120-cell family diminishings that we have found. I don't even know how to name this shape; it's not a luna because the decagonal "joint" where the two cutting hyperplanes meet is off-center, whereas the lunae we found before meet at the center. The o5oxo may be the only shape that admits a CRF result with this kind of strange cutting.
Update: Here's a render centered on the icosahedron (shown in red) antipodal to the decagon joining the two truncated dodecahedra:

The region surrounding the red icosahedron has basically the same structure as the original o5oxo, but it's pretty close to some areas of interest. In particular, two pentagonal pyramids (remains of two icosahedral cells that got truncated by the cutting hyperplanes), shown here in cyan outline, shares a vertex with it. The base of these pentagonal pyramids connect to a pentagonal cupola, the decagonal face of which (shown here in red outline) then interfaces with a truncated dodecahedron on the far side of the polytope (shown in next image). Square pyramids (bisected octahedra) interface this cupola to the intact remnants of the o5oxo. For clarity's sake, I've omitted the other cells visible from this viewpoint.
The next image shows the view from the opposite viewpoint, that is, centered on the decagon joining the two truncated dodecahedra, antipodal to the red icosahedron:

For the sake of clarity, one of the truncated dodecahedra is rendered in yellow, whereas the other one is outlined in red. The decagons opposite the central decagon between the two cells are where the pentagonal cupolae from the first picture connect to these cells. If you can do cross-eyed viewing, you can see outlines of pentagonal cupola wrapping in an alternating pattern all around the central decagon, filling in the gaps between these two truncated dodecahedra which meet at a rather acute angle.
This particular 3D viewpoint gives a false sense of volume due to familiar shapes like truncated dodecahedra, so here's the same projection (same 4D viewpoint) from a different 3D viewpoint, to show how narrow it is, that is, the truncated dodecahedra are being seen from quite a sharp angle.

Since it's past bedtime, I don't have time to show more of the structure of that complex band wrapping around the two truncated dodecahedra, but you can sorta discern that it's an alternating pattern of pentagonal cupolae. There's also a ring of 10 icosahedra that wrap around this band, outside the ring of alternating pentagonal cupolae, not shown in any of these images, because they lie on what's left of the o5oxo's equator: since we're using 4D perspective projection, they're always just barely behind the limb of the projections so we can't see them directly.
Anyway, here are the coordinates of this odd little polychoron:
- Code: Select all
<-(2+sqrt(5)), -(2+sqrt(5)), -1, -1>
<-(2+sqrt(5)), -(2+sqrt(5)), -1, 1>
<-(2+sqrt(5)), -(2+sqrt(5)), 1, -1>
<-(2+sqrt(5)), -(2+sqrt(5)), 1, 1>
<-(2+sqrt(5)), -(5+sqrt(5))/2, 0, -(3+sqrt(5))/2>
<-(2+sqrt(5)), -(5+sqrt(5))/2, 0, (3+sqrt(5))/2>
<-(2+sqrt(5)), -(1+sqrt(5)), (3+sqrt(5))/2, -(1+sqrt(5))/2>
<-(2+sqrt(5)), -(1+sqrt(5)), (3+sqrt(5))/2, (1+sqrt(5))/2>
<-(2+sqrt(5)), -(3+sqrt(5))/2, (1+sqrt(5))/2, -(1+sqrt(5))>
<-(2+sqrt(5)), -(3+sqrt(5))/2, (1+sqrt(5))/2, 1+sqrt(5)>
<-(2+sqrt(5)), -(3+sqrt(5))/2, (5+sqrt(5))/2, 0>
<-(2+sqrt(5)), -(1+sqrt(5))/2, 1+sqrt(5), -(3+sqrt(5))/2>
<-(2+sqrt(5)), -(1+sqrt(5))/2, 1+sqrt(5), (3+sqrt(5))/2>
<-(2+sqrt(5)), -1, 2+sqrt(5), -1>
<-(2+sqrt(5)), -1, 2+sqrt(5), 1>
<-(5+sqrt(5))/2, -(2+sqrt(5)), -(3+sqrt(5))/2, 0>
<-(5+sqrt(5))/2, -(2+sqrt(5)), (3+sqrt(5))/2, 0>
<-(5+sqrt(5))/2, -(3+sqrt(5))/2, 0, -(2+sqrt(5))>
<-(5+sqrt(5))/2, -(3+sqrt(5))/2, 0, 2+sqrt(5)>
<-(5+sqrt(5))/2, 0, 2+sqrt(5), -(3+sqrt(5))/2>
<-(5+sqrt(5))/2, 0, 2+sqrt(5), (3+sqrt(5))/2>
<-(1+sqrt(5)), -(3+sqrt(5)), 0, 0>
<-(1+sqrt(5)), -(2+sqrt(5)), -(1+sqrt(5))/2, -(3+sqrt(5))/2>
<-(1+sqrt(5)), -(2+sqrt(5)), -(1+sqrt(5))/2, (3+sqrt(5))/2>
<-(1+sqrt(5)), -(2+sqrt(5)), (1+sqrt(5))/2, -(3+sqrt(5))/2>
<-(1+sqrt(5)), -(2+sqrt(5)), (1+sqrt(5))/2, (3+sqrt(5))/2>
<-(1+sqrt(5)), -(3+sqrt(5))/2, 2+sqrt(5), -(1+sqrt(5))/2>
<-(1+sqrt(5)), -(3+sqrt(5))/2, 2+sqrt(5), (1+sqrt(5))/2>
<-(1+sqrt(5)), -(1+sqrt(5))/2, (3+sqrt(5))/2, -(2+sqrt(5))>
<-(1+sqrt(5)), -(1+sqrt(5))/2, (3+sqrt(5))/2, 2+sqrt(5)>
<-(1+sqrt(5)), 0, 3+sqrt(5), 0>
<-(3+sqrt(5))/2, -(3+sqrt(5)), -(1+sqrt(5))/2, -1>
<-(3+sqrt(5))/2, -(3+sqrt(5)), -(1+sqrt(5))/2, 1>
<-(3+sqrt(5))/2, -(3+sqrt(5)), (1+sqrt(5))/2, -1>
<-(3+sqrt(5))/2, -(3+sqrt(5)), (1+sqrt(5))/2, 1>
<-(3+sqrt(5))/2, -(2+sqrt(5)), -(1+sqrt(5)), -(1+sqrt(5))/2>
<-(3+sqrt(5))/2, -(2+sqrt(5)), -(1+sqrt(5)), (1+sqrt(5))/2>
<-(3+sqrt(5))/2, -(2+sqrt(5)), 0, -(5+sqrt(5))/2>
<-(3+sqrt(5))/2, -(2+sqrt(5)), 0, (5+sqrt(5))/2>
<-(3+sqrt(5))/2, -(2+sqrt(5)), 1+sqrt(5), -(1+sqrt(5))/2>
<-(3+sqrt(5))/2, -(2+sqrt(5)), 1+sqrt(5), (1+sqrt(5))/2>
<-(3+sqrt(5))/2, -(5+sqrt(5))/2, -(2+sqrt(5)), 0>
<-(3+sqrt(5))/2, -(5+sqrt(5))/2, 2+sqrt(5), 0>
<-(3+sqrt(5))/2, -(1+sqrt(5)), -(1+sqrt(5))/2, -(2+sqrt(5))>
<-(3+sqrt(5))/2, -(1+sqrt(5)), -(1+sqrt(5))/2, 2+sqrt(5)>
<-(3+sqrt(5))/2, -(1+sqrt(5)), (1+sqrt(5))/2, -(2+sqrt(5))>
<-(3+sqrt(5))/2, -(1+sqrt(5)), (1+sqrt(5))/2, 2+sqrt(5)>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, -1, -(3+sqrt(5))>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, -1, 3+sqrt(5)>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, 1, -(3+sqrt(5))>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, 1, 3+sqrt(5)>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, 2+sqrt(5), -(1+sqrt(5))>
<-(3+sqrt(5))/2, -(1+sqrt(5))/2, 2+sqrt(5), 1+sqrt(5)>
<-(3+sqrt(5))/2, -1, 3+sqrt(5), -(1+sqrt(5))/2>
<-(3+sqrt(5))/2, -1, 3+sqrt(5), (1+sqrt(5))/2>
<-(3+sqrt(5))/2, 0, (5+sqrt(5))/2, -(2+sqrt(5))>
<-(3+sqrt(5))/2, 0, (5+sqrt(5))/2, 2+sqrt(5)>
<-(3+sqrt(5))/2, 1, 3+sqrt(5), -(1+sqrt(5))/2>
<-(3+sqrt(5))/2, 1, 3+sqrt(5), (1+sqrt(5))/2>
<-(3+sqrt(5))/2, (1+sqrt(5))/2, 2+sqrt(5), -(1+sqrt(5))>
<-(3+sqrt(5))/2, (1+sqrt(5))/2, 2+sqrt(5), 1+sqrt(5)>
<-(1+sqrt(5))/2, -(5+3*sqrt(5))/2, 0, -1>
<-(1+sqrt(5))/2, -(5+3*sqrt(5))/2, 0, 1>
<-(1+sqrt(5))/2, -(3+sqrt(5)), -1, -(3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(3+sqrt(5)), -1, (3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(3+sqrt(5)), 1, -(3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(3+sqrt(5)), 1, (3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(2+sqrt(5)), -(3+sqrt(5))/2, -(1+sqrt(5))>
<-(1+sqrt(5))/2, -(2+sqrt(5)), -(3+sqrt(5))/2, 1+sqrt(5)>
<-(1+sqrt(5))/2, -(2+sqrt(5)), (3+sqrt(5))/2, -(1+sqrt(5))>
<-(1+sqrt(5))/2, -(2+sqrt(5)), (3+sqrt(5))/2, 1+sqrt(5)>
<-(1+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5)), -(3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5)), (3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5), -(3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5), (3+sqrt(5))/2>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, -(3+sqrt(5)), -1>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, -(3+sqrt(5)), 1>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5))>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5)>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5))>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5)>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, 3+sqrt(5), -1>
<-(1+sqrt(5))/2, -(3+sqrt(5))/2, 3+sqrt(5), 1>
<-(1+sqrt(5))/2, -1, -(3+sqrt(5))/2, -(3+sqrt(5))>
<-(1+sqrt(5))/2, -1, -(3+sqrt(5))/2, 3+sqrt(5)>
<-(1+sqrt(5))/2, -1, (3+sqrt(5))/2, -(3+sqrt(5))>
<-(1+sqrt(5))/2, -1, (3+sqrt(5))/2, 3+sqrt(5)>
<-(1+sqrt(5))/2, -1, (5+3*sqrt(5))/2, 0>
<-(1+sqrt(5))/2, 0, -1, -(5+3*sqrt(5))/2>
<-(1+sqrt(5))/2, 0, -1, (5+3*sqrt(5))/2>
<-(1+sqrt(5))/2, 0, 1, -(5+3*sqrt(5))/2>
<-(1+sqrt(5))/2, 0, 1, (5+3*sqrt(5))/2>
<-(1+sqrt(5))/2, 1, (3+sqrt(5))/2, -(3+sqrt(5))>
<-(1+sqrt(5))/2, 1, (3+sqrt(5))/2, 3+sqrt(5)>
<-(1+sqrt(5))/2, 1, (5+3*sqrt(5))/2, 0>
<-(1+sqrt(5))/2, (3+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5))>
<-(1+sqrt(5))/2, (3+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5)>
<-(1+sqrt(5))/2, (3+sqrt(5))/2, 3+sqrt(5), -1>
<-(1+sqrt(5))/2, (3+sqrt(5))/2, 3+sqrt(5), 1>
<-(1+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5), -(3+sqrt(5))/2>
<-(1+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5), (3+sqrt(5))/2>
<-1, -(5+3*sqrt(5))/2, -(1+sqrt(5))/2, 0>
<-1, -(5+3*sqrt(5))/2, (1+sqrt(5))/2, 0>
<-1, -(3+sqrt(5)), -(3+sqrt(5))/2, -(1+sqrt(5))/2>
<-1, -(3+sqrt(5)), -(3+sqrt(5))/2, (1+sqrt(5))/2>
<-1, -(3+sqrt(5)), (3+sqrt(5))/2, -(1+sqrt(5))/2>
<-1, -(3+sqrt(5)), (3+sqrt(5))/2, (1+sqrt(5))/2>
<-1, -(2+sqrt(5)), -(2+sqrt(5)), -1>
<-1, -(2+sqrt(5)), -(2+sqrt(5)), 1>
<-1, -(2+sqrt(5)), -1, -(2+sqrt(5))>
<-1, -(2+sqrt(5)), -1, 2+sqrt(5)>
<-1, -(2+sqrt(5)), 1, -(2+sqrt(5))>
<-1, -(2+sqrt(5)), 1, 2+sqrt(5)>
<-1, -(2+sqrt(5)), 2+sqrt(5), -1>
<-1, -(2+sqrt(5)), 2+sqrt(5), 1>
<-1, -(3+sqrt(5))/2, -(1+sqrt(5))/2, -(3+sqrt(5))>
<-1, -(3+sqrt(5))/2, -(1+sqrt(5))/2, 3+sqrt(5)>
<-1, -(3+sqrt(5))/2, (1+sqrt(5))/2, -(3+sqrt(5))>
<-1, -(3+sqrt(5))/2, (1+sqrt(5))/2, 3+sqrt(5)>
<-1, -(1+sqrt(5))/2, -(3+sqrt(5)), -(3+sqrt(5))/2>
<-1, -(1+sqrt(5))/2, -(3+sqrt(5)), (3+sqrt(5))/2>
<-1, -(1+sqrt(5))/2, 0, -(5+3*sqrt(5))/2>
<-1, -(1+sqrt(5))/2, 0, (5+3*sqrt(5))/2>
<-1, -(1+sqrt(5))/2, 3+sqrt(5), -(3+sqrt(5))/2>
<-1, -(1+sqrt(5))/2, 3+sqrt(5), (3+sqrt(5))/2>
<-1, -1, -(2+sqrt(5)), -(2+sqrt(5))>
<-1, -1, -(2+sqrt(5)), 2+sqrt(5)>
<-1, -1, 2+sqrt(5), -(2+sqrt(5))>
<-1, -1, 2+sqrt(5), 2+sqrt(5)>
<-1, 0, (5+3*sqrt(5))/2, -(1+sqrt(5))/2>
<-1, 0, (5+3*sqrt(5))/2, (1+sqrt(5))/2>
<-1, 1, 2+sqrt(5), -(2+sqrt(5))>
<-1, 1, 2+sqrt(5), 2+sqrt(5)>
<-1, (1+sqrt(5))/2, 0, -(5+3*sqrt(5))/2>
<-1, (1+sqrt(5))/2, 0, (5+3*sqrt(5))/2>
<-1, (1+sqrt(5))/2, 3+sqrt(5), -(3+sqrt(5))/2>
<-1, (1+sqrt(5))/2, 3+sqrt(5), (3+sqrt(5))/2>
<-1, (3+sqrt(5))/2, (1+sqrt(5))/2, -(3+sqrt(5))>
<-1, (3+sqrt(5))/2, (1+sqrt(5))/2, 3+sqrt(5)>
<-1, 2+sqrt(5), 2+sqrt(5), -1>
<-1, 2+sqrt(5), 2+sqrt(5), 1>
<0, -(5+3*sqrt(5))/2, -1, -(1+sqrt(5))/2>
<0, -(5+3*sqrt(5))/2, -1, (1+sqrt(5))/2>
<0, -(5+3*sqrt(5))/2, 1, -(1+sqrt(5))/2>
<0, -(5+3*sqrt(5))/2, 1, (1+sqrt(5))/2>
<0, -(3+sqrt(5)), -(1+sqrt(5)), 0>
<0, -(3+sqrt(5)), 0, -(1+sqrt(5))>
<0, -(3+sqrt(5)), 0, 1+sqrt(5)>
<0, -(3+sqrt(5)), 1+sqrt(5), 0>
<0, -(2+sqrt(5)), -(5+sqrt(5))/2, -(3+sqrt(5))/2>
<0, -(2+sqrt(5)), -(5+sqrt(5))/2, (3+sqrt(5))/2>
<0, -(2+sqrt(5)), (5+sqrt(5))/2, -(3+sqrt(5))/2>
<0, -(2+sqrt(5)), (5+sqrt(5))/2, (3+sqrt(5))/2>
<0, -(5+sqrt(5))/2, -(3+sqrt(5))/2, -(2+sqrt(5))>
<0, -(5+sqrt(5))/2, -(3+sqrt(5))/2, 2+sqrt(5)>
<0, -(5+sqrt(5))/2, (3+sqrt(5))/2, -(2+sqrt(5))>
<0, -(5+sqrt(5))/2, (3+sqrt(5))/2, 2+sqrt(5)>
<0, -(1+sqrt(5)), -(3+sqrt(5)), 0>
<0, -(1+sqrt(5)), 0, -(3+sqrt(5))>
<0, -(1+sqrt(5)), 0, 3+sqrt(5)>
<0, -(1+sqrt(5)), 3+sqrt(5), 0>
<0, -(3+sqrt(5))/2, -(2+sqrt(5)), -(5+sqrt(5))/2>
<0, -(3+sqrt(5))/2, -(2+sqrt(5)), (5+sqrt(5))/2>
<0, -(3+sqrt(5))/2, 2+sqrt(5), -(5+sqrt(5))/2>
<0, -(3+sqrt(5))/2, 2+sqrt(5), (5+sqrt(5))/2>
<0, -(1+sqrt(5))/2, -(5+3*sqrt(5))/2, -1>
<0, -(1+sqrt(5))/2, -(5+3*sqrt(5))/2, 1>
<0, -(1+sqrt(5))/2, (5+3*sqrt(5))/2, -1>
<0, -(1+sqrt(5))/2, (5+3*sqrt(5))/2, 1>
<0, -1, -(1+sqrt(5))/2, -(5+3*sqrt(5))/2>
<0, -1, -(1+sqrt(5))/2, (5+3*sqrt(5))/2>
<0, -1, (1+sqrt(5))/2, -(5+3*sqrt(5))/2>
<0, -1, (1+sqrt(5))/2, (5+3*sqrt(5))/2>
<0, 0, -(3+sqrt(5)), -(1+sqrt(5))>
<0, 0, -(3+sqrt(5)), 1+sqrt(5)>
<0, 0, -(1+sqrt(5)), -(3+sqrt(5))>
<0, 0, -(1+sqrt(5)), 3+sqrt(5)>
<0, 0, 1+sqrt(5), -(3+sqrt(5))>
<0, 0, 1+sqrt(5), 3+sqrt(5)>
<0, 0, 3+sqrt(5), -(1+sqrt(5))>
<0, 0, 3+sqrt(5), 1+sqrt(5)>
<0, 1, -(1+sqrt(5))/2, -(5+3*sqrt(5))/2>
<0, 1, -(1+sqrt(5))/2, (5+3*sqrt(5))/2>
<0, 1, (1+sqrt(5))/2, -(5+3*sqrt(5))/2>
<0, 1, (1+sqrt(5))/2, (5+3*sqrt(5))/2>
<0, (1+sqrt(5))/2, (5+3*sqrt(5))/2, -1>
<0, (1+sqrt(5))/2, (5+3*sqrt(5))/2, 1>
<0, (3+sqrt(5))/2, 2+sqrt(5), -(5+sqrt(5))/2>
<0, (3+sqrt(5))/2, 2+sqrt(5), (5+sqrt(5))/2>
<0, 1+sqrt(5), 0, -(3+sqrt(5))>
<0, 1+sqrt(5), 0, 3+sqrt(5)>
<0, 1+sqrt(5), 3+sqrt(5), 0>
<0, (5+sqrt(5))/2, (3+sqrt(5))/2, -(2+sqrt(5))>
<0, (5+sqrt(5))/2, (3+sqrt(5))/2, 2+sqrt(5)>
<0, 2+sqrt(5), (5+sqrt(5))/2, -(3+sqrt(5))/2>
<0, 2+sqrt(5), (5+sqrt(5))/2, (3+sqrt(5))/2>
<0, 3+sqrt(5), 1+sqrt(5), 0>
<1, -(5+3*sqrt(5))/2, -(1+sqrt(5))/2, 0>
<1, -(5+3*sqrt(5))/2, (1+sqrt(5))/2, 0>
<1, -(3+sqrt(5)), -(3+sqrt(5))/2, -(1+sqrt(5))/2>
<1, -(3+sqrt(5)), -(3+sqrt(5))/2, (1+sqrt(5))/2>
<1, -(3+sqrt(5)), (3+sqrt(5))/2, -(1+sqrt(5))/2>
<1, -(3+sqrt(5)), (3+sqrt(5))/2, (1+sqrt(5))/2>
<1, -(2+sqrt(5)), -(2+sqrt(5)), -1>
<1, -(2+sqrt(5)), -(2+sqrt(5)), 1>
<1, -(2+sqrt(5)), -1, -(2+sqrt(5))>
<1, -(2+sqrt(5)), -1, 2+sqrt(5)>
<1, -(2+sqrt(5)), 1, -(2+sqrt(5))>
<1, -(2+sqrt(5)), 1, 2+sqrt(5)>
<1, -(2+sqrt(5)), 2+sqrt(5), -1>
<1, -(2+sqrt(5)), 2+sqrt(5), 1>
<1, -(3+sqrt(5))/2, -(1+sqrt(5))/2, -(3+sqrt(5))>
<1, -(3+sqrt(5))/2, -(1+sqrt(5))/2, 3+sqrt(5)>
<1, -(3+sqrt(5))/2, (1+sqrt(5))/2, -(3+sqrt(5))>
<1, -(3+sqrt(5))/2, (1+sqrt(5))/2, 3+sqrt(5)>
<1, -(1+sqrt(5))/2, -(3+sqrt(5)), -(3+sqrt(5))/2>
<1, -(1+sqrt(5))/2, -(3+sqrt(5)), (3+sqrt(5))/2>
<1, -(1+sqrt(5))/2, 0, -(5+3*sqrt(5))/2>
<1, -(1+sqrt(5))/2, 0, (5+3*sqrt(5))/2>
<1, -(1+sqrt(5))/2, 3+sqrt(5), -(3+sqrt(5))/2>
<1, -(1+sqrt(5))/2, 3+sqrt(5), (3+sqrt(5))/2>
<1, -1, -(2+sqrt(5)), -(2+sqrt(5))>
<1, -1, -(2+sqrt(5)), 2+sqrt(5)>
<1, -1, 2+sqrt(5), -(2+sqrt(5))>
<1, -1, 2+sqrt(5), 2+sqrt(5)>
<1, 0, -(5+3*sqrt(5))/2, -(1+sqrt(5))/2>
<1, 0, -(5+3*sqrt(5))/2, (1+sqrt(5))/2>
<1, 0, (5+3*sqrt(5))/2, -(1+sqrt(5))/2>
<1, 0, (5+3*sqrt(5))/2, (1+sqrt(5))/2>
<1, 1, -(2+sqrt(5)), -(2+sqrt(5))>
<1, 1, -(2+sqrt(5)), 2+sqrt(5)>
<1, 1, 2+sqrt(5), -(2+sqrt(5))>
<1, 1, 2+sqrt(5), 2+sqrt(5)>
<1, (1+sqrt(5))/2, -(3+sqrt(5)), -(3+sqrt(5))/2>
<1, (1+sqrt(5))/2, -(3+sqrt(5)), (3+sqrt(5))/2>
<1, (1+sqrt(5))/2, 0, -(5+3*sqrt(5))/2>
<1, (1+sqrt(5))/2, 0, (5+3*sqrt(5))/2>
<1, (1+sqrt(5))/2, 3+sqrt(5), -(3+sqrt(5))/2>
<1, (1+sqrt(5))/2, 3+sqrt(5), (3+sqrt(5))/2>
<1, (3+sqrt(5))/2, -(1+sqrt(5))/2, -(3+sqrt(5))>
<1, (3+sqrt(5))/2, -(1+sqrt(5))/2, 3+sqrt(5)>
<1, (3+sqrt(5))/2, (1+sqrt(5))/2, -(3+sqrt(5))>
<1, (3+sqrt(5))/2, (1+sqrt(5))/2, 3+sqrt(5)>
<1, 2+sqrt(5), -1, -(2+sqrt(5))>
<1, 2+sqrt(5), -1, 2+sqrt(5)>
<1, 2+sqrt(5), 1, -(2+sqrt(5))>
<1, 2+sqrt(5), 1, 2+sqrt(5)>
<1, 2+sqrt(5), 2+sqrt(5), -1>
<1, 2+sqrt(5), 2+sqrt(5), 1>
<1, 3+sqrt(5), (3+sqrt(5))/2, -(1+sqrt(5))/2>
<1, 3+sqrt(5), (3+sqrt(5))/2, (1+sqrt(5))/2>
<1, (5+3*sqrt(5))/2, (1+sqrt(5))/2, 0>
<(1+sqrt(5))/2, -(5+3*sqrt(5))/2, 0, -1>
<(1+sqrt(5))/2, -(5+3*sqrt(5))/2, 0, 1>
<(1+sqrt(5))/2, -(3+sqrt(5)), -1, -(3+sqrt(5))/2>
<(1+sqrt(5))/2, -(3+sqrt(5)), -1, (3+sqrt(5))/2>
<(1+sqrt(5))/2, -(3+sqrt(5)), 1, -(3+sqrt(5))/2>
<(1+sqrt(5))/2, -(3+sqrt(5)), 1, (3+sqrt(5))/2>
<(1+sqrt(5))/2, -(2+sqrt(5)), -(3+sqrt(5))/2, -(1+sqrt(5))>
<(1+sqrt(5))/2, -(2+sqrt(5)), -(3+sqrt(5))/2, 1+sqrt(5)>
<(1+sqrt(5))/2, -(2+sqrt(5)), (3+sqrt(5))/2, -(1+sqrt(5))>
<(1+sqrt(5))/2, -(2+sqrt(5)), (3+sqrt(5))/2, 1+sqrt(5)>
<(1+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5)), -(3+sqrt(5))/2>
<(1+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5)), (3+sqrt(5))/2>
<(1+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5), -(3+sqrt(5))/2>
<(1+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5), (3+sqrt(5))/2>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, -(3+sqrt(5)), -1>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, -(3+sqrt(5)), 1>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5))>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5)>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5))>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5)>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, 3+sqrt(5), -1>
<(1+sqrt(5))/2, -(3+sqrt(5))/2, 3+sqrt(5), 1>
<(1+sqrt(5))/2, -1, -(5+3*sqrt(5))/2, 0>
<(1+sqrt(5))/2, -1, -(3+sqrt(5))/2, -(3+sqrt(5))>
<(1+sqrt(5))/2, -1, -(3+sqrt(5))/2, 3+sqrt(5)>
<(1+sqrt(5))/2, -1, (3+sqrt(5))/2, -(3+sqrt(5))>
<(1+sqrt(5))/2, -1, (3+sqrt(5))/2, 3+sqrt(5)>
<(1+sqrt(5))/2, -1, (5+3*sqrt(5))/2, 0>
<(1+sqrt(5))/2, 0, -1, -(5+3*sqrt(5))/2>
<(1+sqrt(5))/2, 0, -1, (5+3*sqrt(5))/2>
<(1+sqrt(5))/2, 0, 1, -(5+3*sqrt(5))/2>
<(1+sqrt(5))/2, 0, 1, (5+3*sqrt(5))/2>
<(1+sqrt(5))/2, 1, -(5+3*sqrt(5))/2, 0>
<(1+sqrt(5))/2, 1, -(3+sqrt(5))/2, -(3+sqrt(5))>
<(1+sqrt(5))/2, 1, -(3+sqrt(5))/2, 3+sqrt(5)>
<(1+sqrt(5))/2, 1, (3+sqrt(5))/2, -(3+sqrt(5))>
<(1+sqrt(5))/2, 1, (3+sqrt(5))/2, 3+sqrt(5)>
<(1+sqrt(5))/2, 1, (5+3*sqrt(5))/2, 0>
<(1+sqrt(5))/2, (3+sqrt(5))/2, -(3+sqrt(5)), -1>
<(1+sqrt(5))/2, (3+sqrt(5))/2, -(3+sqrt(5)), 1>
<(1+sqrt(5))/2, (3+sqrt(5))/2, -(1+sqrt(5)), -(2+sqrt(5))>
<(1+sqrt(5))/2, (3+sqrt(5))/2, -(1+sqrt(5)), 2+sqrt(5)>
<(1+sqrt(5))/2, (3+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5))>
<(1+sqrt(5))/2, (3+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5)>
<(1+sqrt(5))/2, (3+sqrt(5))/2, 3+sqrt(5), -1>
<(1+sqrt(5))/2, (3+sqrt(5))/2, 3+sqrt(5), 1>
<(1+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5)), -(3+sqrt(5))/2>
<(1+sqrt(5))/2, 1+sqrt(5), -(2+sqrt(5)), (3+sqrt(5))/2>
<(1+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5), -(3+sqrt(5))/2>
<(1+sqrt(5))/2, 1+sqrt(5), 2+sqrt(5), (3+sqrt(5))/2>
<(1+sqrt(5))/2, 2+sqrt(5), -(3+sqrt(5))/2, -(1+sqrt(5))>
<(1+sqrt(5))/2, 2+sqrt(5), -(3+sqrt(5))/2, 1+sqrt(5)>
<(1+sqrt(5))/2, 2+sqrt(5), (3+sqrt(5))/2, -(1+sqrt(5))>
<(1+sqrt(5))/2, 2+sqrt(5), (3+sqrt(5))/2, 1+sqrt(5)>
<(1+sqrt(5))/2, 3+sqrt(5), -1, -(3+sqrt(5))/2>
<(1+sqrt(5))/2, 3+sqrt(5), -1, (3+sqrt(5))/2>
<(1+sqrt(5))/2, 3+sqrt(5), 1, -(3+sqrt(5))/2>
<(1+sqrt(5))/2, 3+sqrt(5), 1, (3+sqrt(5))/2>
<(1+sqrt(5))/2, (5+3*sqrt(5))/2, 0, -1>
<(1+sqrt(5))/2, (5+3*sqrt(5))/2, 0, 1>
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:Thus the chosen segmentochora seem to be restricted to one of the followings: tet||oct, tet||co, tut||toe, {4}||cube, or line||cube, which then shall occur as caps at the corresponding axes. (Oct||co e.g. disqualifies because the top base likewise has the higher symmetry. And tut||co disqualifies too, as tut has the larger circumradius and thus co is not the bottom base, which has to be incident to the cut.)
--- rk
I don't think this is entirely true -- in some polychora, you can also cut off segmentochoron with a 2n-gonal prism as a cap. For example, a o3x3o5x has a cap of 5gon||10prism which could be gyrated.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
quickfur wrote:I have discovered another CRF diminishing of the o5oxo: a "meta"-bathodiminishing. This is produced by two deep cuttings of the o5oxo, each of which truncates it up to a truncated dodecahedron cross-section. Unlike the previous "meatball sandwich" cutting I posted earlier, though, in which the two cutting hyperplanes are parallel, in this one the hyperplanes make an angle of 72°. It just so happens that the two resulting truncated dodecahedra meet at a decagonal face, thus producing a peculiar spindle-like wedge structure with 31 icosahedra, 2 truncated dodecahedra, 22 pentagonal cupola, 120 octahedra, 12 pentagonal pyramids, and some other cells (I haven't counted them all yet), for a total of 287 cells. The pentagonal cupola wrap around the decagonal face between the two truncated dodecahedra, and are rimmed by a ring of 10 icosahedra around them.
Indeed, here is its lace city display:
- Code: Select all
x5x
x5o o5F
F5o o5V
o5o f5f
o5f x5F
x5f F5x F5x
x5o V5o V5o
x5F x5F
F5o F5o F=ff=x+f=2x+v,
x5x f5f F5F f5f x5x V=F+v=2f=2x+2v
o5F o5F
F5x F5x
o5x o5V o5V
f5x x5F x5F
f5o F5x
o5o f5f
o5F V5o
o5x F5o
x5x
@quicfur: you should give a try for such a side view display too!
Finally, this lace city also Shows that you even could chopp off that left "red" icosahedron, even in a bistratic manner, i.e. resulting there in a parabidiminished rhombicosidodecahedron!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:Finally, in order to have at all the possibility of a gyration, the sectioning facet polytope should have a higher symmetry than that of the corresponding axis! Within the Johnsonians this is achieved rather easily: the axis is 3-, 4-, or 5-fold, but the base of the corresponding cupolae (or rotunda) are hexagons, octagons, resp. decagons. For polychora this is much harder. We have axes with tetrahedral, octahedral, or icosahedral symmetry. Thus the only sectioning facet polyhedra with a similar higher symmetry are o3x3o (octahedron within a tetrahedral context), x3o3x (cuboctahedron within a tetrahedral context), and x3x3x (truncated octahedron within a tetrahedral context). That is, we have to look for such polychora where some segmentochoral cap can be chopped off, which uses right these polyhedra for there bottom base and have tetrahedral axial symmetry.
Brique symmetry might look also be possible, but there clearly is just one non-degenerate bottom base which has higher symmetry: x2x2x (cube). But note that such an axis would occure only within (degenerate) 2,P-duoprisms, i.e. either x2x2xPo = x4o2xPo or x2x2xPx = x4o2x2Po.
(Suppose that's all. At least I don't see any further such subsymmetry right now.)
Thus the chosen segmentochora seem to be restricted to one of the followings: tet||oct, tet||co, tut||toe, {4}||cube, or line||cube, which then shall occur as caps at the corresponding axes. (Oct||co e.g. disqualifies because the top base likewise has the higher symmetry. And tut||co disqualifies too, as tut has the larger circumradius and thus co is not the bottom base, which has to be incident to the cut.)
Marek14 wrote:I don't think this is entirely true -- in some polychora, you can also cut off segmentochoron with a 2n-gonal prism as a cap. For example, a o3x3o5x has a cap of 5gon||10prism which could be gyrated.
Ah yes, you are right. So not only digonal prism symmetries (o2o2o) would be supported, but N-gonal as well. But the essence would remain so ever: you need some axial subsymmetry which allows for supersymmetries, i.e. in its Dynkin symbol display there is some symbol immanent additional symmetry possible.
So additional to my above mentioned tetrahedral cases there should be N-gon || 2N-prism and N-prism || 2N-prism, for CRF clearly N=2 (my already mentioned case), 3, 4, or 5 (one of which you were exampling above). - Thank you.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Basically, as I tried some time ago, if you have a verf of a uniform polychoron, then anything that can be inscribed in it is a possible CRF cut. For example, in case of srahi, the verf is a wedge with topology of triangular prism. Each diagonal of the quadrigonal faces corresponds to a cut (cutting octagon in two square pyramids or cutting a pentagonal cupola off of rhombicosidodecahedron). By slicing off vertices of this verf, we can therefore cut off a decagonal prism or a truncated dodecahedron.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Klitzing wrote:quickfur wrote:I have discovered another CRF diminishing of the o5oxo: a "meta"-bathodiminishing. This is produced by two deep cuttings of the o5oxo, each of which truncates it up to a truncated dodecahedron cross-section. Unlike the previous "meatball sandwich" cutting I posted earlier, though, in which the two cutting hyperplanes are parallel, in this one the hyperplanes make an angle of 72°. It just so happens that the two resulting truncated dodecahedra meet at a decagonal face, thus producing a peculiar spindle-like wedge structure with 31 icosahedra, 2 truncated dodecahedra, 22 pentagonal cupola, 120 octahedra, 12 pentagonal pyramids, and some other cells (I haven't counted them all yet), for a total of 287 cells. The pentagonal cupola wrap around the decagonal face between the two truncated dodecahedra, and are rimmed by a ring of 10 icosahedra around them.
Indeed, here is its lace city display:
[...snipped...]
You can spot at the left (vertical column) the "red" icosahedron and at the right the single decagon. The 2 truncated dodecahedra are the slanting sides of this wedge (ASCII graphic here is not too exact: those should align instead of wobbling around...). Thus it is nothing but a huge decagon-icosahedron-wedge. Its wedge angle clearly would not be 72 but rather 36 degrees.
You're right, it's 36°, not 72°. My bad.

@quicfur: you should give a try for such a side view display too!
Yes, I was planning to. Maybe later today when I have a bit of free time.
Finally, this lace city also Shows that you even could chopp off that left "red" icosahedron, even in a bistratic manner, i.e. resulting there in a parabidiminished rhombicosidodecahedron!
[...]
I did notice that, actually. I didn't mention it 'cos I wanted to construct it first, but you went ahead of me.

In fact, I was considering if it may be possible to trim the shape to a nicely-symmetric, maximal diminishing -- maximal meaning, cannot be diminished any further without becoming non-CRF. The further truncation that produces a J80 is just one of the possible next steps; I think some of the other cells admit further truncations too, so they can be trimmed down to the "bare minimum" in some way.
So actually, we could regard this polychoron as an "augmented" decagon-J80 wedge, since the "red" icosahedron isn't really necessary in a minimal construction.

In the process of constructing the current diminishing, I realized that actually there are a lot more CRF diminishings of the 120-cell family of uniforms than I previously thought, because previously, I had written off diminishings that cause non-CRF truncations of existing cells. However, I failed to take into account the case where these non-CRF truncated cells can simply be removed from the result when their bases are CRF, since then they can be replaced by CRF "filler" cells. This happens with the "bisected" 600-cell: 12 florets of 5 tetrahedra each get bisected in a non-CRF way, but that didn't present a problem since they could simply be removed and have pentagonal pyramids fill up their place. Now I see that this isn't just an isolated lucky case; it's a general phenomenon that can happen in many (though not all) cases.
This means that it's actually possible to cut, for example, the 600-cell into CRF strata, by replacing any non-CRF truncated tetrahedra with pentagonal pyramids where applicable. So every stratum in the sequence o5oo||o5ox||x5oo||o5xo||x5oo||o5ox||o5oo form CRF segmentochora which can be derived by cutting the 600-cell along parallel hyperplanes then "patching" the non-CRF parts with pentagonal pyramids. The 600-cell is just the simplest case, of course; other 120-cell family polychora can also be stratified in this way (though not all admit CRF stratifications, e.g., when the cutting hyperplane cross a o5ox in the wrong orientation, and there are no CRF polyhedra that can patch that up to make a CRF result). The appearance of the pentagonal cupola in the bathodiminishings of o5oxo was what gave me this realization. There should be many other cases where this kind of "CRF-able" truncations can happen in the 120-cell family.
Edit: haha, I just realized that I rambled on for 2 paragraphs basically just repeating what Marek just said in a concise way.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:[...]@quicfur: you should give a try for such a side view display too![...]
Alright, here's the side-view of the metabathobidiminished o5oxo:
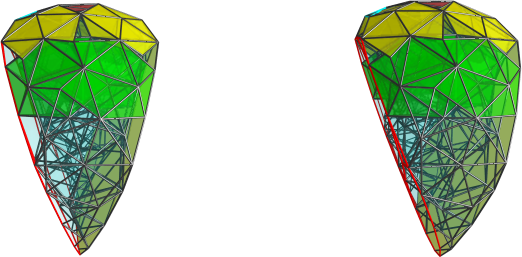
The red outline on the left is the (image of the) red-outlined truncated dodecahedron from the previous renders; the dark yellow flat surface on the right is the other truncated dodecahedron.
The red blob at the top of the image is the red icosahedron from the previous renders; here it's seen at the limb of the projection so it appears flat. The 10 yellow icosahedra can be seen at the layer just below the red icosahedron. You can sortof see that they form a layer that can be further diminished to yield a J80 connecting the tops of the two truncated dodecahedra. The green layer is where we had the alternating cycle of 10 green icosahedra from the previous renders. Immediately below them is the ring of 10 icosahedra I was talking about (I was too lazy to color them this time). Underneath them, in the sharpest part of the wedge, is where there's a layer of alternating pentagonal cupolae.
So in this projection, the wedge shape is very clearly seen. It's also clear that many more diminishings are possible while preserving the overall wedge shape: we can cut off the top red and yellow icosahedra, for example; but also the uncolored icosahedra just above the sharp joint of the wedge can have the vertices where each icosahedron touches the other in the ring deleted, which would turn the ring into a 20-membered ring of alternating pentagonal prisms and pentagonal antiprisms. The layer of green icosahedra can also be diminished in similar ways. I haven't investigated yet what's the maximal diminishing possible. That is, what's the smallest CRF shape that still contains the x5xo--J80--x5xo cycle?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Well, let's see... o5oxo has a pentagonal prism as verf. A pentagonal prism has several of possible facets.
Apart from normal octahedra and icosahedra, there are rhombicosidodecahedral cuts (cutting octahedra in half and diminishing icosahedra), truncated dodecahedra, icosidodecahedra (diminishing icosahedra) and pentagonal prisms (cutting off vertices). Here's where the three levels of diminishing flow from organically. As for multiple diminishings -- do we actually have enumerated the number of possible n-diminishings on this symmetry group?
Apart from normal octahedra and icosahedra, there are rhombicosidodecahedral cuts (cutting octahedra in half and diminishing icosahedra), truncated dodecahedra, icosidodecahedra (diminishing icosahedra) and pentagonal prisms (cutting off vertices). Here's where the three levels of diminishing flow from organically. As for multiple diminishings -- do we actually have enumerated the number of possible n-diminishings on this symmetry group?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Right you are Marek.
The pentagonal prism, i.e. the vertex figure of rox = o3x3o5o, has several differently sized vertex connections:
First consider the possible vertex-inscribed triangles. Those are
An even more elaborate Investigation, using likewise non-convex faceting polygons, was done in HedronDude's research for uniform polychora. In fact he investigates all facetings of possible vertex figures, in order to derive the vertex figures of all regiment members. The rox regiment eg. is nicely diplayed at http://www.polytope.net/hedrondude/rox.htm.
--- rk
The pentagonal prism, i.e. the vertex figure of rox = o3x3o5o, has several differently sized vertex connections:
- Those connectin adjacent vertices. These correspond to the shortchords of triangles.
- Those, which are diametrals of the lateral squares. Thus obviously those are shortchords of squares.
- Then there are connections of non-adjacent vertices of a single pentagon. Obviously the shortchords of pentagons.
- Finally there are connections kind of diametrically underneath the formers, connecting a vertex of the bottom base to a (nearly) diametrically opposite vertex of the top base. Those come out to have the length of the shortchord of a decagon.
First consider the possible vertex-inscribed triangles. Those are
- 3-3-4 (bottom verf of squippy)
- 3-3-5 (bottom verf of peppy)
- 3-4-10 (bottom verf of pecu)
- 3-5-5 (eg used in mibdi or teddi)
- 3-5-10 (bottom verf of pero)
- 3-10-10 (tid)
- 4-4-5 (pip)
- 4-5-10 (eg used in dirid, pabidrid, mabidrid, tedrid)
- 3-3-3-3 (oct or tip verf of squippy)
- 3-3-3-5 (used in gyepip, pap, mibdi, or teddi)
- 3-4-5-4 (used in pecu, srid, dirid, pabidrid, mabidrid, or tedrid)
- 3-5-3-5 (used in id or pero)
- 3-3-3-3-3 (used at tip of peppy, in ike, or mibdi)
An even more elaborate Investigation, using likewise non-convex faceting polygons, was done in HedronDude's research for uniform polychora. In fact he investigates all facetings of possible vertex figures, in order to derive the vertex figures of all regiment members. The rox regiment eg. is nicely diplayed at http://www.polytope.net/hedrondude/rox.htm.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
On 18. December I posted my then newest finding
Within the last days I now derived a close relative convex segmentoteron: tico || prissi.
What does this one look like?
Tico is the Wythoffian polyteron called "truncated icositetrachoron", x3x4o3o. It will be used for top base.
The bottom base is even more intricating. It is prissi, the convex and just scaliform polychoron (which I once found myself in September 2005 - because it uses the non-uniform triangular cupolae as some of its cells), meanwhile being called "prismatorhombisnub icositetrachoron". (More details on that one can be found at the prissi-page of my incmats-website, including further links. Btw, meanwhile it even can be found at Wikipedia.)
Prissi in those days was derived as an alternated faceting, in fact as s3s4o3x, i.e. by chopping off alternate ". . o3x"-triangle caps from x3x4o3x (prico) and applying an afterwards relaxation towards all unit edges. That this relaxation truely is possible, in those days was proven by Wendy by means of Stott expansion from s3s4o3o (sadi, snub icositetrachoron). HedronDude then found out additionally, that it can be derived by a mere diminishing from padohi (x3o5o5/2x). This can be seen by consideration of the vertex figures of both: that of prissi is a (convex) faceting of that of padohi.
So, this exceptional figure now will be included in this segmentoteron for bottom base.
How did I derive that?
I just reconsidering the above again cited posting: there I described rico || sadi, i.e. o3o4x3o || s3s4o3o. So it seems appropriate to apply a similar Stott expansion to either base, i.e. towards o3o4x3x || s3s4o3x. The problem here is that we interchange 2 operations, i.e. alternated faceting (including the afterwards applied relaxation!) and Stott expansion. And furthermore, it is not only that we try to align those 2 base polychora atop of each other, we still have to derive whether there can be according lacing cells. So again we interchange 2 operations. - So far this seemed all allowed in this case, esp. from knowing os3os4xo3oo&#x to exist. - But finally, I tried to derive the full 5D alternated faceting from the according first derived lace prism ox3ox4xo3xx&#y (note that y here has to be an edge much longer than x in order to exist) including the afterwards to be applied Relaxation, instead of a mere stacking of tico and the before 4D-derived alternated faceting. - I.e. once again a switch of operations.
All this finally turned out to be valid. Thus we are truely allowed to write os3os4xo3xx&#x for that fellow.
So, what then is the structure of that one?
(Incidence matrix could be provided, if desired. I've already elaborated that one. )
)
The height of that segmentoteron is the same as that of rico||sadi, i.e. sqrt[(sqrt(5)-1)/2] = 0.786151 (cf. the then corrected mail).
The 5D circumradius thus can be calculated as sqrt[(27+13 sqrt(5))/8] = 2.647378.
--- rk
Klitzing wrote:Having now provided (in my recent mail of this thread) that segmentochoral gem, the cube || ike, in a (partially) snubbed lace prism notation, i.e. as os3os4xo&#x, it gets quite immediate where to find higher dimensional CRFs, which would contain right that fellow for subelements.
In fact, today I've evaluated the convex segmentoteron rico || sadi. It turns out, that it not only belongs to the right geometry (all edges can be chosen to have the same unit length, without drifting then into euclidean space (height becoming zero) or even an hyperbolic one (height becoming imaginary)), by construction it additionally solves that mentioned problem as well.
...
How did I get to consider rico || sadi? - Just by extension of the Dynkin symbol of that mentioned segmentochoron: Accordingly its incidence matrix too can be derived from os3os4xo3oo&#x as
...
Its facets thus are: 1x rico as top base, 24x cube || ike, 24x co || tet, 96x trippy (here coming in as {3} || tet, for sure), and 1x sadi as bottom base. - Its polyhedral elements, now given cummulative, are 24x cube, 24x co, 24x ike, 288x squippy, 312x tet, and 240x trip. - It uses 1152 triangles and 432 squares. - It has a total of 1008 edges and 192 vertices.
Fascinating, ain't it?
--- rk
Within the last days I now derived a close relative convex segmentoteron: tico || prissi.
What does this one look like?
Tico is the Wythoffian polyteron called "truncated icositetrachoron", x3x4o3o. It will be used for top base.
The bottom base is even more intricating. It is prissi, the convex and just scaliform polychoron (which I once found myself in September 2005 - because it uses the non-uniform triangular cupolae as some of its cells), meanwhile being called "prismatorhombisnub icositetrachoron". (More details on that one can be found at the prissi-page of my incmats-website, including further links. Btw, meanwhile it even can be found at Wikipedia.)
Prissi in those days was derived as an alternated faceting, in fact as s3s4o3x, i.e. by chopping off alternate ". . o3x"-triangle caps from x3x4o3x (prico) and applying an afterwards relaxation towards all unit edges. That this relaxation truely is possible, in those days was proven by Wendy by means of Stott expansion from s3s4o3o (sadi, snub icositetrachoron). HedronDude then found out additionally, that it can be derived by a mere diminishing from padohi (x3o5o5/2x). This can be seen by consideration of the vertex figures of both: that of prissi is a (convex) faceting of that of padohi.
So, this exceptional figure now will be included in this segmentoteron for bottom base.
How did I derive that?
I just reconsidering the above again cited posting: there I described rico || sadi, i.e. o3o4x3o || s3s4o3o. So it seems appropriate to apply a similar Stott expansion to either base, i.e. towards o3o4x3x || s3s4o3x. The problem here is that we interchange 2 operations, i.e. alternated faceting (including the afterwards applied relaxation!) and Stott expansion. And furthermore, it is not only that we try to align those 2 base polychora atop of each other, we still have to derive whether there can be according lacing cells. So again we interchange 2 operations. - So far this seemed all allowed in this case, esp. from knowing os3os4xo3oo&#x to exist. - But finally, I tried to derive the full 5D alternated faceting from the according first derived lace prism ox3ox4xo3xx&#y (note that y here has to be an edge much longer than x in order to exist) including the afterwards to be applied Relaxation, instead of a mere stacking of tico and the before 4D-derived alternated faceting. - I.e. once again a switch of operations.
All this finally turned out to be valid. Thus we are truely allowed to write os3os4xo3xx&#x for that fellow.
So, what then is the structure of that one?
- It has 192 vertices at the top base (tico) and 288 vertices at the bittom base (prissi). Thus 480 vertices in total.
- It uses 384 top edges, 576 lacing ones, and 1008 bottom ones. Thus 1968 edges in total.
- Polygons are 144 squares and 96 hexagons in the top base, 864 lacing triangles and 576 lacing squares, as well as 576 triangles, 288 squares, and 96 hexagons at the bottom base. Thus 1440 triangles, 1008 squares, and 192 hexagons in total.
- Polyhedra will be 24 cubes, 24 toes, 192 tricues, 192 tets, 528 trips, 288 squippies, 96 hips, 24 ikes, and 24 tuts.
- Polychora are 1 tico (top base), 24 cube||ike, 96 tepes (used as line||trip), 24 toe||tut, 96 {3}||hip (used as {6}||tricu instead) plus 1 prissi (bottom base).
(Incidence matrix could be provided, if desired. I've already elaborated that one.
 )
)The height of that segmentoteron is the same as that of rico||sadi, i.e. sqrt[(sqrt(5)-1)/2] = 0.786151 (cf. the then corrected mail).
The 5D circumradius thus can be calculated as sqrt[(27+13 sqrt(5))/8] = 2.647378.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
that thing is just awesome. I still don't really understand what polytopes with both an s and an x look like, although I do understand the construction proces.Klitzing wrote:On 18. December I posted my then newest findingKlitzing wrote:[...]
Within the last days I now derived a close relative convex segmentoteron: tico || prissi.
What does this one look like?
[...]
--- rk
btw. I just thought of doing this with other snubs as well. Have you thought of demicube-things? e.g. so4ox3ox3oo&#x. This is just a 16-cell atop a o4x3x3o, but the 16-cell is oriented differently. (maybe you can have so4ox3ox3xx&#x etc. as well)
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
thank you!student91 wrote:that thing is just awesome.
I still don't really understand what polytopes with both an s and an x look like, although I do understand the construction proces.
Best would be to consider "s4o3x" for that reason: starting figure there is "x4o3x", i.e. sirco (small rhombicuboctahedron). The alternated elements (of that starting figure) then would be the elements ". o3x", i.e. the triangles. The to be chopped off caps thus would be (if still undistorted) "oq3xx&#x", resp. the sectioning facet underneath would thus be (still undistorted) ". q3x", i.e. hexagons. Having 8 triangles in the starting figure, those will be alternated thus into 4 remaining ones plus 4 which are to be replaced by those hexagons (the sefas). All the squares of rhombical positions ("x . x") would then be reduced to one of their sides (those incident to the remaining triangles) by means of edge alternation, and the squares in cubical positions ("x4o .") would be reduced to their diagonal by means of vertex alternation. Therefore the mere alternated faceting would come out (unrelaxed) as what could be alternatively be described as "q3x3o". (Here, just as always, Wendy's q-edge is sqrt(2) times larger than x.) Thus the relaxed Version of "s4o3x" is nothing but the (then again uniform version of the) truncated tetrahedron.
btw. I just thought of doing this with other snubs as well. Have you thought of demicube-things? e.g. so4ox3ox3oo&#x. This is just a 16-cell atop a o4x3x3o, but the 16-cell is oriented differently. (maybe you can have so4ox3ox3xx&#x etc. as well)
I surely did several such or similar investigations, but for the specific ones I first have to go through my notes first. The main issue here always would be not only that both bases belong to the same symmetry, allow for unit edges only individually, but that a unit edge lacing can be applied in between, which generates a neither imaginary nor degenerate (zero) height.
By view of Stott addition the question about so4ox3ox3xx&#x is not too difficult to answer: it should exist as soon as so4ox3ox3oo&#x does exist. And both then would have the same height.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:student91 wrote:btw. I just thought of doing this with other snubs as well. Have you thought of demicube-things? e.g. so4ox3ox3oo&#x. This is just a 16-cell atop a o4x3x3o, but the 16-cell is oriented differently. (maybe you can have so4ox3ox3xx&#x etc. as well)
I surely did several such or similar investigations, but for the specific ones I first have to go through my notes first. The main issue here always would be not only that both bases belong to the same symmetry, allow for unit edges only individually, but that a unit edge lacing can be applied in between, which generates a neither imaginary nor degenerate (zero) height.
By view of Stott addition the question about so4ox3ox3xx&#x is not too difficult to answer: it should exist as soon as so4ox3ox3oo&#x does exist. And both then would have the same height.
--- rk
Hmm, sad to disappoint you for those:
R(hex) = 1/sqrt(2) = 0.707, R(tah) = sqrt(9/2) = 2.121.
Thus there cannot be any unit lacing, independent from every orientation!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:Hmm, sad to disappoint you for those:
R(hex) = 1/sqrt(2) = 0.707, R(tah) = sqrt(9/2) = 2.121.
Thus there cannot be any unit lacing, independent from every orientation!
--- rk
that's indeed a pitty. luckily, there are possibly much more demicube-based polytera.
the way you seem to make snub-based segmentotera is by taking a snub-based segmentochoron and add 3oo resp. 3xx to it.
the demicube (3D->tetahedron) gives quite a lot possible segmentochora. They stay unnoticed, because the huge overlap between the tetahedral and the octahedral wythoffians.
s4o3o can be placed atop anything with the first node unringed (so o4%3%) (only topolgically speaking).
this gives so4o%3o%3oo&#x and so4o%3o%3xx&#x. I think these will give topologically valid CRF's. the lacing edges should be checked to be unity-able.
s4o3o can also be placed atop s4o3o where the latter is alternated the other way around, I'll denotate that as s+s-4oo3oo&#x. This gives s+s-4oo3oo3oo&#x and s+s-4oo3oo3xx&#x
now s4o3x. it again can be placed atop o4%3%, giving so4o%3x%3oo&#x and so4o%3x%3xx&#x.
s+4o3x can furthermore be placed atop s+4o3o and s-4o3x, giving s+s-4oo3xx3oo&#x, s+s-4oo3xx3xx&#x, ss4oo3ox3oo&#x and ss4oo3ox3xx&#x.
s4x3% doesn't seem to be that special, at least I didn't bother investigating it
 .
.again, those are only topologically correct. the height hasn't been checked (at least not by me).
Besides, I missed a important feature of my segmentitopical product when I was equalling it to duoprism-stack analysis. my segmentotopical product also applies to irregular segmentotopes (eg line ||triangle). these can't be written in wendy's lacing notation, so my product sign ¤ still keeps unused
 .
.EDIT: I just realized that there are no irregular segmentohedra, because triangle||line = x(xo)&#x and line ||square = x(xx)&#x. ¤ will still not be used, because those are just duoprism-lace-simplices. (when you'd multiply xx5ox&#x with xxo&#x, you just place two copies of x5o, so xxx5oxo2xxo&#x.) There are irregular segmentochora, e.g. K4.169
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
Yes s+s-4oo3oo3oo&#x clearly is possible.
Consider the following:
s4o3o...3o is nothing but x3o3o *b3o...3o (using the same number of nodes), i.e. the according demihypercube. (Esp. you'd need at least 3 nodes.) But you always can rewrite any demihypercube (with 4 or more nodes) as a convex segmentotope, in fact as xo3oo3ox *b3oo...3oo&#x (with one node less). The height of that stack then will be dimension independently always 1/sqrt(2).
This gyrated usage of demihypercubes within this stack is just what you rewrites by the alternate applications of s+ resp. s- within the 2 layers.
Stott addition then furthermore allows for any additional ringing of those nodes (in either layer at the same positions for sure) which are (both) unringed so far. This would not even change the height of the resulting segmentotopes.
What becomes different here in these examples to the cases I pointed out, is that you generally would have to apply the snubbing of the bases first, including their relaxations to unit edges, and then would have to apply stacking thereafter. There seems to be no general way for commuting those processes. - But mine examples clearly did allow for a first stacking of the starting figures, and thereafter applying a then D+1-dimensional alternated faceting!
(At least I do not see such a way in general, so far.)
This commutation of operations was what I wanted to underline by calling mine as partial snubs, i.e. choosing to be alternated elements only from one layer, even so the alternated faceting still will be a D+1 dimensional process.
--- rk
Consider the following:
s4o3o...3o is nothing but x3o3o *b3o...3o (using the same number of nodes), i.e. the according demihypercube. (Esp. you'd need at least 3 nodes.) But you always can rewrite any demihypercube (with 4 or more nodes) as a convex segmentotope, in fact as xo3oo3ox *b3oo...3oo&#x (with one node less). The height of that stack then will be dimension independently always 1/sqrt(2).
This gyrated usage of demihypercubes within this stack is just what you rewrites by the alternate applications of s+ resp. s- within the 2 layers.
Stott addition then furthermore allows for any additional ringing of those nodes (in either layer at the same positions for sure) which are (both) unringed so far. This would not even change the height of the resulting segmentotopes.
What becomes different here in these examples to the cases I pointed out, is that you generally would have to apply the snubbing of the bases first, including their relaxations to unit edges, and then would have to apply stacking thereafter. There seems to be no general way for commuting those processes. - But mine examples clearly did allow for a first stacking of the starting figures, and thereafter applying a then D+1-dimensional alternated faceting!
(At least I do not see such a way in general, so far.)
This commutation of operations was what I wanted to underline by calling mine as partial snubs, i.e. choosing to be alternated elements only from one layer, even so the alternated faceting still will be a D+1 dimensional process.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
I mainly keep an eye here because i am moderator and it's active.
But the discussion is interesting, if over my head. I've been wrangling the dozenalists at the moment.
Suppose it's s4o3o3o3o. I would not get too excited here.
Student91 mentions line || triangle. This is a three-base lace-prism, oxx&#x. I know Richard was trying to trick me with this one earlier.
This is actually o5o3x3o. It's also a vertex-figure of o5o3o3oAx.
But the discussion is interesting, if over my head. I've been wrangling the dozenalists at the moment.
Klitzing wrote:Yes s+s-4oo3oo3oo&#x clearly is possible.
Suppose it's s4o3o3o3o. I would not get too excited here.
Student91 mentions line || triangle. This is a three-base lace-prism, oxx&#x. I know Richard was trying to trick me with this one earlier.
Marek14 wrote:o5oxo
This is actually o5o3x3o. It's also a vertex-figure of o5o3o3oAx.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Johnsonian Polytopes
I like that ...wendy wrote:...
But the discussion is interesting, if over my head.
Haha, where elseI've been wrangling the dozenalists at the moment.
Completely correct.Klitzing wrote:Yes s+s-4oo3oo3oo&#x clearly is possible.
Suppose it's s4o3o3o3o.
Me neither, old known stuff, that one.I would not get too excited here.
...
But one should stay fair and try to not disappoint newcommers overly much when they rediscover things on their own ...
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:Yes s+s-4oo3oo3oo&#x clearly is possible.
[...]
What becomes different here in these examples to the cases I pointed out, is that you generally would have to apply the snubbing of the bases first, including their relaxations to unit edges, and then would have to apply stacking thereafter. There seems to be no general way for commuting those processes. - But mine examples clearly did allow for a first stacking of the starting figures, and thereafter applying a then D+1-dimensional alternated faceting!
(At least I do not see such a way in general, so far.)
This commutation of operations was what I wanted to underline by calling mine as partial snubs, i.e. choosing to be alternated elements only from one layer, even so the alternated faceting still will be a D+1 dimensional process.
--- rk
I thought of it the following way: a (n-1)-based segmentotope has a (n-1)-symmetry group, e.g. .P.Q.R.S...., yielding %%P%%Q%%R%%S%%...&#x.
in every fundamental domain exactly 2×1 "seed point" will be placed (one for every layer). the seedpoints that have the same fundamental domain should be connected, and no otherr connections should be made.
Now if you'd put a "s" in it, you will skip one domain. in order to be connected nicely, the other polytope should have an o where this one has an s. This makes that the seed point will be at an edge where the thing is alternated, meaning that it will connect nicely (this part isn't completely consistent).
whatever, that part was rubbish. what I'm trying to say is that by looking at it as hyperspheres concentrically placed atop each other, there might be a theorem makeable for connecting snubs. (I'm mainly thingking about wythoff-snub-things here: |p q r. it's a general way of snubbing, that could also be applied for goursat tetahedra and maybe even further. Therefore, the connections may be (topologically) determined. not sure about this though. Besides, could you tell me why snubs aren't wythhoffian, while they do have a wythoff-symbol. it seems counterntuitive to me. was the |p q r introduced by someone else or something?)
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
Klitzing wrote:Completely correct.wendy wrote:Klitzing wrote:Yes s+s-4oo3oo3oo&#x clearly is possible.
Suppose it's s4o3o3o3o.
Ah, now I get what you might have been telling here. That s+s-4oo3oo3oo&#x in fact can be given in the commuted sense (referred in my original mail) too: first stacking x4o3o3o atop x4o3o3o, then applying a 5D alternation. Here it applies to all vertices, but still thereby one might take the POV of layers, so that in the top layer you'd alternate the one way (+) and at the bottom layer you'd alternate the other one (-). Yes, this works indeed. And thus you'd result in s4o3o3o3o directly.
But still, it is not a partial snub, as the choice of to be alternated elements recombines the 2 layers into one single 5D polyteron, i.e. will be evenly applied through both layers. Partial snubs OTOH would respect this extra axial dimension and thus choose elements just from a single layer instead. (Or, more generally, from some subsymmetrical subset.)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:Yes s+s-4oo3oo3oo&#x clearly is possible.
Consider the following:
s4o3o...3o is nothing but x3o3o *b3o...3o (using the same number of nodes), i.e. the according demihypercube. (Esp. you'd need at least 3 nodes.) But you always can rewrite any demihypercube (with 4 or more nodes) as a convex segmentotope, in fact as xo3oo3ox *b3oo...3oo&#x (with one node less). The height of that stack then will be dimension independently always 1/sqrt(2).
[...]
--- rk
I indeed rediscovered that
 . means that the demicube-things won't be overlooked anyway.
. means that the demicube-things won't be overlooked anyway. but what does s3s3s3s4o look like? i mean, s3s4o is a icosahedron, s3s3s4o is a diminished 600-cell, and so s3s3s3s4o might have some interesting 5-fold symmetry things as well (although it's not uniform)
besides, you once said this:
Klitzing wrote:student91 wrote:Note that there's another (quite obvious) diminishing of o3x3o5o: just cut out a single vertex. The resulting gap will be a pentagonal prism. Maybe we can call this a micro-diminishing?
There might be also some octahedron-centered diminishings. [...]
Is this way of looking at it useful?
student91
Exactly this Investigation has been done already, e.g. cf. http://bendwavy.org/klitzing/incmats/rox.htm, section "Vertex layers": not only the possible uniform polytopes within the section hyperplane are given, in fact all, i.e. using other edge lengths, and for any relevant subsymmetry. Note also the leftmost numbering of layers: within several instances those polytopes cannot given directly, rather they tend to be compounds of several coincident ones.
The same analysis is provided for lots of other polytopes as well, so not all
(Feel free to mail me further additions.)
--- rk
could you tell me what polytopes haven't got such an ionvestigation?
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
student91 wrote:Besides, could you tell me why snubs aren't wythhoffian, while they do have a wythoff-symbol. it seems counterntuitive to me. was the |p q r introduced by someone else or something?)
That term does not refer to the W. symbol, it rather refers to the kaleidoscopical construction device of W. As you can see from your pic, the snubs do not allow for such a construction, they do need for 2 elementary cells. This is why.
Btw. I simply use that term ("Wythoffian" polytopes) as a synonyme to the much longer explanation that I'd consider all those polytopes, which allow for Dynkin symbols which use only x and o for node symbols. As those such restricted Dynkin symbols readily describe nothing but the application of that kaleidoscopical construction...
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
student91 wrote:besides, you once said this:Klitzing wrote:student91 wrote:Note that there's another (quite obvious) diminishing of o3x3o5o: just cut out a single vertex. The resulting gap will be a pentagonal prism. Maybe we can call this a micro-diminishing?
There might be also some octahedron-centered diminishings. [...]
Is this way of looking at it useful?
student91
Exactly this Investigation has been done already, e.g. cf. http://bendwavy.org/klitzing/incmats/rox.htm, section "Vertex layers": not only the possible uniform polytopes within the section hyperplane are given, in fact all, i.e. using other edge lengths, and for any relevant subsymmetry. Note also the leftmost numbering of layers: within several instances those polytopes cannot given directly, rather they tend to be compounds of several coincident ones.
The same analysis is provided for lots of other polytopes as well, so not all
(Feel free to mail me further additions.)
--- rk
could you tell me what polytopes haven't got such an ionvestigation?
Even so this is an Investigation in progress, I have not done too much on that recently. So most of that would be online. Just go through the individual linked incmats pages. I would have to look there (or rather: in my off-line working copy) as well...
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Klitzing wrote:student91 wrote:[...]
That term does not refer to the W. symbol, it rather refers to the kaleidoscopical construction device of W. As you can see from your pic, the snubs do not allow for such a construction, they do need for 2 elementary cells. This is why.
Btw. I simply use that term ("Wythoffian" polytopes) as a synonyme to the much longer explanation that I'd consider all those polytopes, which allow for Dynkin symbols which use only x and o for node symbols. As those such restricted Dynkin symbols readily describe nothing but the application of that kaleidoscopical construction...
--- rk
ah, okay.
but that those thigs need two different "fundamental domains," I hope that doesn't mean the concentric hypersphere-view will be invalid.
this view, if investigated, may give a answer to whether so4%%3%%...%%3%%&#x is possible.
nvm. so4%%... will always be subsitutable into a demicube thing.
student91
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Re: Johnsonian Polytopes
Klitzing wrote:[...]
But one should stay fair and try to not disappoint newcommers overly much when they rediscover things on their own ...
[...]
I agree. Often I find that I understand something much better when I rediscover it on my own, rather than just read it from a textbook or have somebody tell me. A quote attributed to Benjamin Franklin: "Tell me and I forget. Teach me and I remember. Involve me and I understand." I think this is especially true when it comes to visualizing higher-dimensional objects. The process of understanding is simply the process of (re)discovery.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Wythoff is not guilty of the notation this. The notation is actually a form of 'decorated schwarz triangle'. The schwarz triangle corresponds to "p q r", without the bar symbol. If you put the bar right at the beginning, like '| 2 3 5', it corresponds to a point, ie what we write o3o5o. We just leave that as a point, because we have a use for points with icosahedral symmetry, (eg o3o5o || x3o5o = ox3oo5oo&#x 'icosaheral pyramid'.
The people who invented this symbol were doing in 3D, a thing which HedronDude has done for four dimensions, and is now gracing our lists with the five and six dimensional versions: non-convex uniform polytopes. It's just that there is exactly one snub per group, and one point, so you can rename the point into the snub.
Wythoff's main contribution here is to demonstrate that Stott's expansions and contractions could all be done with mirrors, but he never got past writing something like t0,1,2 C600, for what we write x3x3x5o. Coxeter discovered a neat name for the kaleidoscopes (derived from Schläfli symbol), and Wythoff hacked Stott's notation enough so that Coxeter could write t0,1,2{3,3,5}.
But none of them got as far as writing them in-line like i do. Coxeter will draw pretty pictures in text, like @-----@-----o. But they stay like that, they are not reduced to x3x3o or anything, despite what Klitzing says. (rk thought coxeter invented my notation ) You are probably lucky for my notation, because Coxeter had nested subscripts in x3x3x3x3x3x3xBx (ie 4_21 with every node marked). I shudder to think what he would do with 'varieties' (ie when you stick q or f or h for x). John Conway follows Coxeter's notation to the t (except he uses a 'ambi' there, even though a2 {3,3,5} o3o3x5o is not both ways of anything! Also you have to remember Coxeter and others are using zero count, where i mark the individual nodes.
) You are probably lucky for my notation, because Coxeter had nested subscripts in x3x3x3x3x3x3xBx (ie 4_21 with every node marked). I shudder to think what he would do with 'varieties' (ie when you stick q or f or h for x). John Conway follows Coxeter's notation to the t (except he uses a 'ambi' there, even though a2 {3,3,5} o3o3x5o is not both ways of anything! Also you have to remember Coxeter and others are using zero count, where i mark the individual nodes.
Calling a 'decorated schwarz triangle' a 'Wythof symobl' was seen by a mob of maths professors (including Coxeter, who really should have known better), as a neat way of honouring Wythoff and throwing everyone else (including me), off the track. Wythoff has nothing to do with Schwarz triangles, decorated or not.
The reason we don't accept them as 'wythoff-figures', is because it's not made of edges that are perpendicular to mirrors that form a simplex cell. This is really important, because we have fancy rules and spreadsheets that you can stick these edges into, and it pulls out the size of the figure, and whatever else you want. But 's' isn't an edge that is cut in two by a mirror. No wythoff figure here.
Stott Snubs
It's actually alicia stott who suggested to donald coxeter, that it would be a neat idea to represent the snubs, if you circle the dots on the CD diagram, and then remove the inner dot (because there's no mirror). Coxeter agreed. But they never got down to calling these anything: there's only something like three or four uniform snubs, and since Coxeter was not really interested in the non-uniform ones, things like s3s3s3s went begging.
s3s3s3s is actually quite interesting. It's got 60 vertices, 60 tetrahedra, 20 octahedra, and 10 icosahedra for its faces. But unlike 3d, where every snub must exist with uniform edges, in four dimensions, it's more luck than good management.
See, if you take something like xPxQx, and turn it into sPsQs, you get three different edge lengths in xPxQx, and you have a triangle with three edges, so it's down to solving (in general) a cubic, and pulling a cubic-like solution. s3s5s solves equations of the sixth degree (ie x^6+...), and the s3s4s solves a cubic (ie x^3+...)
In four dimensions, you get xPxQxRx, which means you can set four different edges freely. But the tetrahedron has six edges, and you generally can't solve six equations in four variables. When you do an amount of symmetrising, you reduce things somewhat.
xPyQyPx has two degrees of freedom (x, y), but the tetrahedron has three kinds of edges. No go.
xPxPyAPx or xPyPx4o or yPx4o3o. Here you have two degrees of freedom, but the vertex figure is a triangle pyramid, the triangle is equalateral. There are two variables, and two kinds of edge, so a solution always arise (ie P=3, x=1, y=1.618033 or something). This has a solution always, for yPx4o3o.....
x2Po3o3o3... Here the vertex figure is a simplex, there is one edge, and one degree of freedom. It is solved always.
s3s3s3s4o no doubt exists. It would be a quite interesting figure made of the s3s3s4o = s3s4o3o 'snub 24choron', and the s3s3s3s. But like s3s3s3s (which is one of its faces), it's not uniform
The people who invented this symbol were doing in 3D, a thing which HedronDude has done for four dimensions, and is now gracing our lists with the five and six dimensional versions: non-convex uniform polytopes. It's just that there is exactly one snub per group, and one point, so you can rename the point into the snub.
student91 wrote:wythoff-symbol. it seems counterntuitive to me. was the |p q r introduced by someone else or something?)Image
Wythoff's main contribution here is to demonstrate that Stott's expansions and contractions could all be done with mirrors, but he never got past writing something like t0,1,2 C600, for what we write x3x3x5o. Coxeter discovered a neat name for the kaleidoscopes (derived from Schläfli symbol), and Wythoff hacked Stott's notation enough so that Coxeter could write t0,1,2{3,3,5}.
But none of them got as far as writing them in-line like i do. Coxeter will draw pretty pictures in text, like @-----@-----o. But they stay like that, they are not reduced to x3x3o or anything, despite what Klitzing says. (rk thought coxeter invented my notation
 ) You are probably lucky for my notation, because Coxeter had nested subscripts in x3x3x3x3x3x3xBx (ie 4_21 with every node marked). I shudder to think what he would do with 'varieties' (ie when you stick q or f or h for x). John Conway follows Coxeter's notation to the t (except he uses a 'ambi' there, even though a2 {3,3,5} o3o3x5o is not both ways of anything! Also you have to remember Coxeter and others are using zero count, where i mark the individual nodes.
) You are probably lucky for my notation, because Coxeter had nested subscripts in x3x3x3x3x3x3xBx (ie 4_21 with every node marked). I shudder to think what he would do with 'varieties' (ie when you stick q or f or h for x). John Conway follows Coxeter's notation to the t (except he uses a 'ambi' there, even though a2 {3,3,5} o3o3x5o is not both ways of anything! Also you have to remember Coxeter and others are using zero count, where i mark the individual nodes. Calling a 'decorated schwarz triangle' a 'Wythof symobl' was seen by a mob of maths professors (including Coxeter, who really should have known better), as a neat way of honouring Wythoff and throwing everyone else (including me), off the track. Wythoff has nothing to do with Schwarz triangles, decorated or not.
The reason we don't accept them as 'wythoff-figures', is because it's not made of edges that are perpendicular to mirrors that form a simplex cell. This is really important, because we have fancy rules and spreadsheets that you can stick these edges into, and it pulls out the size of the figure, and whatever else you want. But 's' isn't an edge that is cut in two by a mirror. No wythoff figure here.
Stott Snubs
It's actually alicia stott who suggested to donald coxeter, that it would be a neat idea to represent the snubs, if you circle the dots on the CD diagram, and then remove the inner dot (because there's no mirror). Coxeter agreed. But they never got down to calling these anything: there's only something like three or four uniform snubs, and since Coxeter was not really interested in the non-uniform ones, things like s3s3s3s went begging.
s3s3s3s is actually quite interesting. It's got 60 vertices, 60 tetrahedra, 20 octahedra, and 10 icosahedra for its faces. But unlike 3d, where every snub must exist with uniform edges, in four dimensions, it's more luck than good management.
See, if you take something like xPxQx, and turn it into sPsQs, you get three different edge lengths in xPxQx, and you have a triangle with three edges, so it's down to solving (in general) a cubic, and pulling a cubic-like solution. s3s5s solves equations of the sixth degree (ie x^6+...), and the s3s4s solves a cubic (ie x^3+...)
In four dimensions, you get xPxQxRx, which means you can set four different edges freely. But the tetrahedron has six edges, and you generally can't solve six equations in four variables. When you do an amount of symmetrising, you reduce things somewhat.
xPyQyPx has two degrees of freedom (x, y), but the tetrahedron has three kinds of edges. No go.
xPxPyAPx or xPyPx4o or yPx4o3o. Here you have two degrees of freedom, but the vertex figure is a triangle pyramid, the triangle is equalateral. There are two variables, and two kinds of edge, so a solution always arise (ie P=3, x=1, y=1.618033 or something). This has a solution always, for yPx4o3o.....
x2Po3o3o3... Here the vertex figure is a simplex, there is one edge, and one degree of freedom. It is solved always.
s3s3s3s4o no doubt exists. It would be a quite interesting figure made of the s3s3s4o = s3s4o3o 'snub 24choron', and the s3s3s3s. But like s3s3s3s (which is one of its faces), it's not uniform

The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Johnsonian Polytopes
wendy wrote:Wythoff is not guilty of the notation this. The notation is actually a form of 'decorated schwarz triangle'. [...] since Coxeter was not really interested in the non-uniform ones, things like s3s3s3s went begging.
thanks for that explanation, it was very explanatory
s3s3s3s is actually quite interesting. It's got 60 vertices, 60 tetrahedra, 20 octahedra, and 10 icosahedra for its faces. But unlike 3d, where every snub must exist with uniform edges, in four dimensions, it's more luck than good management.
See, if you take something like xPxQx, and turn it into sPsQs, you get three different edge lengths in xPxQx, and you have a triangle with three edges, so it's down to solving (in general) a cubic, and pulling a cubic-like solution. s3s5s solves equations of the sixth degree (ie x^6+...), and the s3s4s solves a cubic (ie x^3+...)
In four dimensions, you get xPxQxRx, which means you can set four different edges freely. But the tetrahedron has six edges, and you generally can't solve six equations in four variables. When you do an amount of symmetrising, you reduce things somewhat.
xPyQyPx has two degrees of freedom (x, y), but the tetrahedron has three kinds of edges. No go.
xPxPyAPx or xPyPx4o or yPx4o3o. Here you have two degrees of freedom, but the vertex figure is a triangle pyramid, the triangle is equalateral. There are two variables, and two kinds of edge, so a solution always arise (ie P=3, x=1, y=1.618033 or something). This has a solution always, for yPx4o3o.....
x2Po3o3o3... Here the vertex figure is a simplex, there is one edge, and one degree of freedom. It is solved always.
s3s3s3s4o no doubt exists. It would be a quite interesting figure made of the s3s3s4o = s3s4o3o 'snub 24choron', and the s3s3s3s. But like s3s3s3s (which is one of its faces), it's not uniform
thanks for the explanation why the snubs don't exist. I never really understood why it was impossible.
I recently realized that s3s3s3s4o=s3s3s*b3s3s, more generally ...s3s3s3s4o=s3s3s*b3s3s... i.e. full-snub demicube
that still doesn't make things very clear, but at least I know what it is now.
How easily one gives his confidence to persons who know how to give themselves the appearance of more knowledge, when this knowledge has been drawn from a foreign source.
-Stern/Multatuli/Eduard Douwes Dekker
-Stern/Multatuli/Eduard Douwes Dekker
- student91
- Tetronian
- Posts: 328
- Joined: Tue Dec 10, 2013 3:41 pm
Who is online
Users browsing this forum: Google [Bot] and 14 guests
