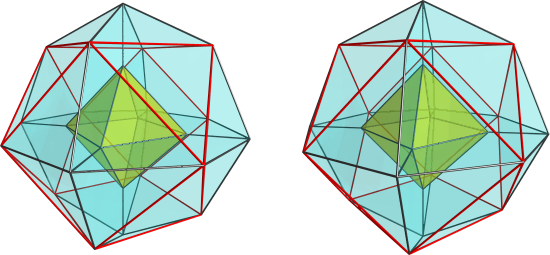Keiji wrote:quickfur wrote:Keiji wrote:Another point to ponder: knowing the existence of the BXD (bixylodiminished hydrochoron) as well as the higher-dimensional ursatopes, does this mean there are equivalents to the BXD in 5D and up, one for each ursatope, which are also chiral, CRF, vertex- and cell-transitive? Or perhaps they would only exist in even dimensions 6D, 8D etc, due to the spiralling structure required?
I believe you need even dimensions to get the higher-dimensional equivalent of the Hopf fibration (which is what the BXD is based on). But this is just a wild guess, so I might be completely wrong.
And teddies aren't
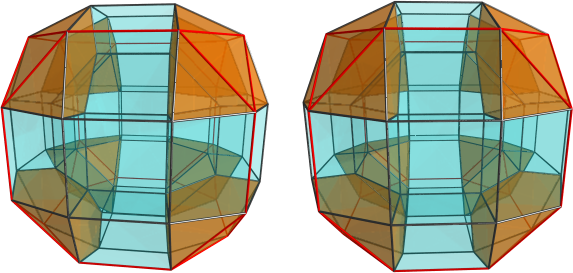
required for these things; all the regular polychora (except perhaps the 5-cell) exhibit this spiralling structure. The bitruncated 24-cell does, too (and probably the bitruncated 5-cell as well). The tesseractic family mainly exhibit the 2-ring structure of the duoprisms (which is a subset of this spiralling symmetry -- think the first ring and the equatorial ring). The 24-cell family exhibits the 8-ring structure you see in the BXD. The 120-cell family exhibits more spiralling rings -- 12 of them, IIRC. But we just don't notice it because there are too many other interesting symmetries that obscure it.

That all makes sense, but see my bolded conditions above - the regular polytopes aren't chiral.

Well, then you've found a new direction to search for CRF polychora in.

Also, it's interesting that the duoprisms are a special case with 2 rings - what are the possibilities with respect to number of rings? Does it have to be even, is there a maximum, are there polychora with 6 or 10 rings?
I'm not 100% certain on this, but according to what I understand, the idea behind the Hopf fibration is to map every point on a sphere to a distinct great circle on the 3-sphere. None of these great circles intersect each other, but they fill up the surface of the 3-sphere in a swirling manner. Of course, there are a continuum of points on the sphere, so this doesn't give us a discrete structure; Bowers' insight was to notice that the swirlprism corresponded with a discrete version of the Hopf fibration, in the sense that the base shape divided the surface of the sphere into equal regions, so that one may now group the great circles according to which region of the sphere would fall on them. This produces a finite number of groups of circles (which you can think of as a finite number of rings, if you consider all circles in the same group as being represented by the ring associated with that group). The cells of the swirlprism thus lies along these rings.
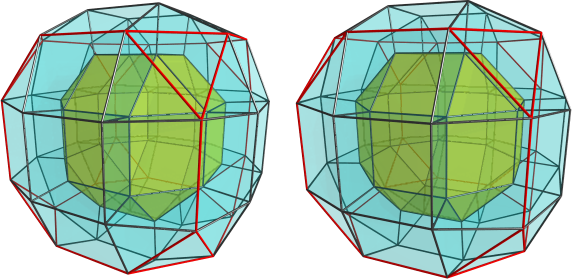
Since the discrete rings arise from the division of the surface of the sphere into regions, you would get a regular structure out of it if you used a regular division of the sphere's surface, that is, if you started with the regular polyhedra. You can also start with the digon, which (I believe) gives you duoprism symmetry, that is, two orthogonal rings. The tetrahedron gives a 4-ring structure; the cube gives a 6-ring structure, the octahedron gives an 8-ring structure, the dodecahedron, 12 rings, and the icosahedron, 20 rings.
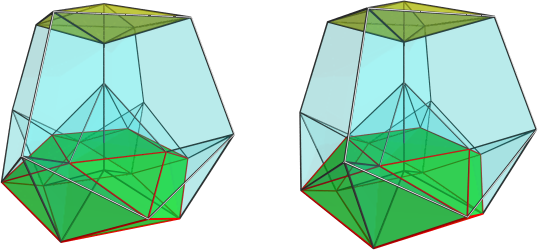
These are just the regular divisions, of course. If you start with uniform polyhedra, you'll get other ring combinations; the truncated cube, for example, will give you a 14-ring structure, grouped into two distinct set of rings each with 8 and 6 rings, respectively. You can start with other polyhedra as well, including non-symmetric ones, in which case you'll just get non-equivalent rings. You may or may not be able to get CRFs out of these non-regular rings. The upper limit is really the continuum, i.e., the Hopf fibration itself, in which you start from the sphere (as a "polyhedron" with infinite number of faces). But as far as
regular rings are concerned, you only have the 5 Platonic solids and the digon, so the maximum there is 20 rings (which, I suspect, will correspond with something derived from the 120-cell family).




 The icosidodecahedron is o3x5o, not x3o5x.
The icosidodecahedron is o3x5o, not x3o5x.