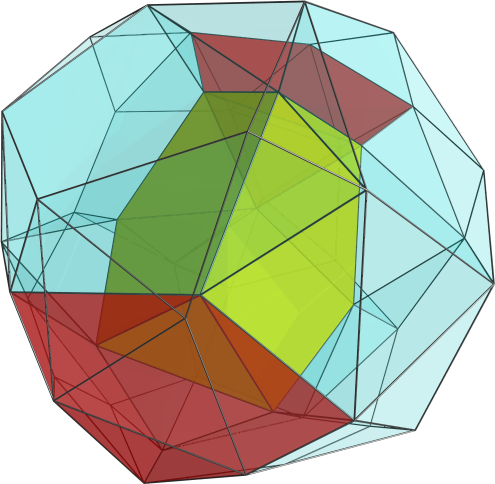
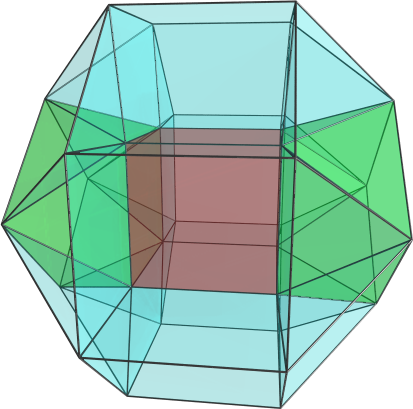
quickfur wrote:All right, so I've calculated the coordinates of the bi-icositetradiminished 600-cell by hand. [...]
OK, here are the coordinates:
- Code: Select all
<0, 1, ±φ, 1/φ>
<0, -1, φ, ±1/φ>
<0, ±1, -φ, -1/φ>
<0, 1/φ, 1, ±φ>
<0, -1/φ, ±1, φ>
<0, ±1/φ, -1, -φ>
<0, φ, ±1/φ, -1>
<0, -φ, 1/φ, ±1>
<0, ±φ, -1/φ, 1>
< 1, 0, -1/φ, ±φ>
<-1, 0, ±1/φ, φ>
<±1, 0, 1/φ, -φ>
< 1, 1/φ, ±φ, 0>
<-1, ±1/φ, φ, 0>
<±1, -1/φ, -φ, 0>
< 1, φ, 0, ±1/φ>
<-1, ±φ, 0, 1/φ>
<±1, -φ, 0, -1/φ>
< 1/φ, 0, φ, ±1>
<-1/φ, 0, ±φ, -1>
<±1/φ, 0, -φ, 1>
< 1/φ, ±1, 0, φ>
<-1/φ, 1, 0, ±φ>
<±1/φ, -1, 0, -φ>
< 1/φ, ±φ, 1, 0>
<-1/φ, φ, ±1, 0>
<±1/φ, -φ, -1, 0>
< φ, 0, 1, ±1/φ>
<-φ, 0, ±1, 1/φ>
<±φ, 0, -1, -1/φ>
< φ, ±1, -1/φ, 0>
<-φ, 1, ±1/φ, 0>
<±φ, -1, 1/φ, 0>
< φ, 1/φ, 0, ±1>
<-φ, ±1/φ, 0, -1>
<±φ, -1/φ, 0, 1>
where φ is the Golden Ratio, (1+√5)/2.
These are basically the coordinates of the snub 24-cell (even permutations and all changes of sign of <φ, 1, 1/φ, 0>), minus an inscribed 24-cell. The 24-cell was found by decomposing it into a 16-cell plus a tesseract:
- First, we choose a pair of antipodal points to be the first axis of the 16-cell;
- Then we take advantage of the fact that the equatorial points of the 16-cell all have zero dot product with first pair of points. So we look for a permutation of <φ, 1, 1/φ, 0> that has zero dot product with the first point; that point with its antipode forms the second axis of the 16-cell.
- Again, the remaining axes of the 16-cell must have zero dot product with the previous two pairs of points, so we go through and find the third pair; the fourth pair is found the same way.
Next, we find the vertices of the tesseract by noting that, since the tesseract must compose with the 16-cell to form a 24-cell, the line segment from the origin to each vertex must pass through the centroid of the corresponding cell in the 16-cell. So we simply add the vectors of each cell in the 16-cell to find the tangent vector, and then scale it so that it is a permutation of <φ, 1, 1/φ, 0>.
- How do we know which vectors to add? It's easy: the 16-cell's vertices are expressed as 4 pairs of vectors of the form ±<A,B,C,D>. Since cells never contain both points of a single axis, and antipodes differ merely in sign, every cell is simply a sum of some combination of coordinate signs of the representative point of each of the 4 pairs. There are exactly 2^4 combinations of signs, so we just enumerate binary numbers from 0000 to 1111, and take 0 to mean + and 1 to mean -, and so we obtain tangent vectors to the 16-cell's facets.
- These sums turn out to be exactly 2*some permutation of <φ, 1, 1/φ, 0>, so the vertices of the tesseract are directly obtained in this way.
So this gives us the vertices of a 24-cell inscribed in the snub 24-cell. To get the coordinates of the bi-icositetradiminished 600-cell, then, we just enumerate the even permutations of <φ, 1, 1/φ, 0>, minus the vertices of this 24-cell.
(I have this nagging feeling that there's a shorter way to obtain these coordinates, but this way is relatively straightforward and in any case, is how I found the coordinates. I did have another idea of how to find these coordinates, by taking advantage of the correspondence of the snub 24-cell's icosahedra with the cells of a tesseract + a 16-cell along with their orientations, which form a sort of non-parallel orientation assignment of the tesseract's cells (the 4D analog of bisecting the cube's faces such that no two adjacent faces are bisected by the same plane), but eventually it turned out to involve exactly the same calculations as I describe above, and is more complicated to deal with to boot. So if you have a better way to do this, I'm all ears.

)
(you've just said it is non-convex, so why is it on the the list of CRF polychora?) that's what I was asking
based on what yous aid it should be under a list of shapes that tesselate!!!



 Looks nice.
Looks nice.