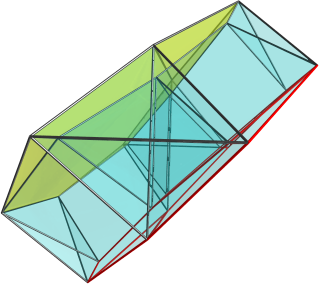
Keiji wrote:quickfur wrote:Thanks so much!! Yes, it's confirmed. All edge lengths are equal, and there are 6 square antiprisms, 1 cube and 1 cuboctahedron. Here's an image:
I'm repeating myself, but can you render a version with the cube inside/outside the cuboctahedron instead of stacked vertically?
Funny you asked, I did try that viewpoint but found the edges overlapping too much in the 2D view, so I switched to another view.

But since you asked:

I don't know about you, I just generally prefer to see 3+1 forms rendered with the +1 on the in-out dimension.

I generally like the W axis to be vertical, so that I can see it as a 4Der would, resting on a 4D desk.

Although I do use other views quite frequently too.
Also, here's something I'm surprised I haven't asked before: why don't you release your program and polytope files so others can rotate things as they please?

Actually, that is a very good idea.
Although, I have to warn you that it is a command-line application, and there's no GUI
at all. Although there are some shorthand commands, it is intended more for scripts, so even at the command-line it can be a bit tedious to use. The intention is really for scripts that auto-render the images on my website, so it's streamlined that way. Because of this, it only generates POVray meshes, and not even complete povray scenes. You have to write a wrapper scene file along with your own textures and import the generated mesh, set up textures and povray camera, etc.. You can define povray textures in the viewer, but the format is very limited so for complicated textures you probably want to just declare it in your povray scene file and only use the texture name in the viewer. There is a hackish command for setting the povray transform inside the viewer program so that you don't have to keep editing the povray scene file.
The convex hull algo is not implemented in the viewer itself; a separate program reads vertices or bounding hyperplanes in Komei Fukuda's "Polyhedra format", and generates the polytope definition that the viewer uses. There are also a bunch of auxiliary utilities for generating vertices of various stuff; most of these output Polyhedra format that you then have to feed to the convex hull program to generate the definition. The viewer only understands the definition files. I am actually thinking of rewriting the polytope generation utilities and merge them into one, together with the convex hull algo, so that you can use a single program for generating all kinds of polytopes. And one day this might be integrated into the viewer as well, i'm not sure yet.
And there are also many areas that really need to be improved, but I haven't had the time/interest to do it because i haven't needed to use those features that much yet or they are too complicated to implement in a short time, so they will have to wait until i have more time. There are also poor performance algorithms that really need to be improved.
Oh, and the code uses some UNIX-specific stuff, so you may have trouble compiling it on windows unless you have cygwin or similar.
If you're still interested, let me know.




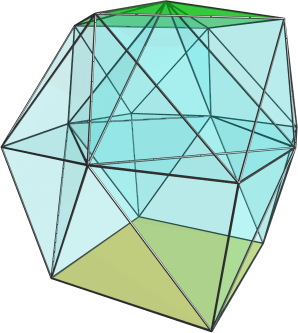
 I see where is mistake. Yes, 9 octahedra are here
I see where is mistake. Yes, 9 octahedra are here  But they are in the model that my program generated.
But they are in the model that my program generated.



 Although I do use other views quite frequently too.
Although I do use other views quite frequently too. I will probably have to do arbitrary 3D CSG, which is a pain to code.
I will probably have to do arbitrary 3D CSG, which is a pain to code.