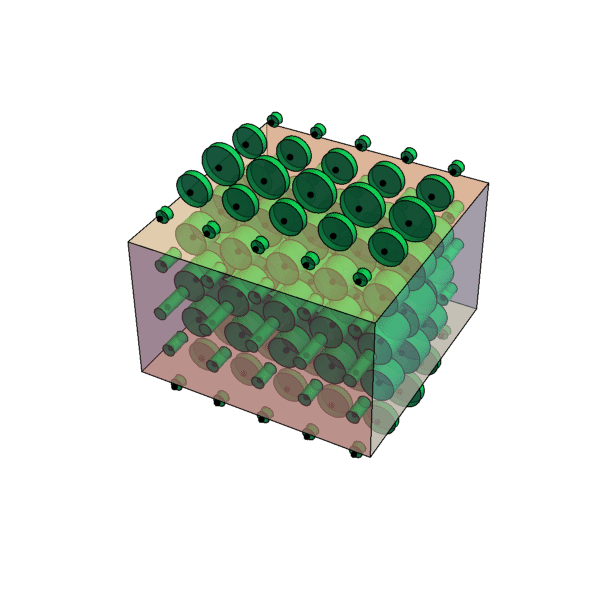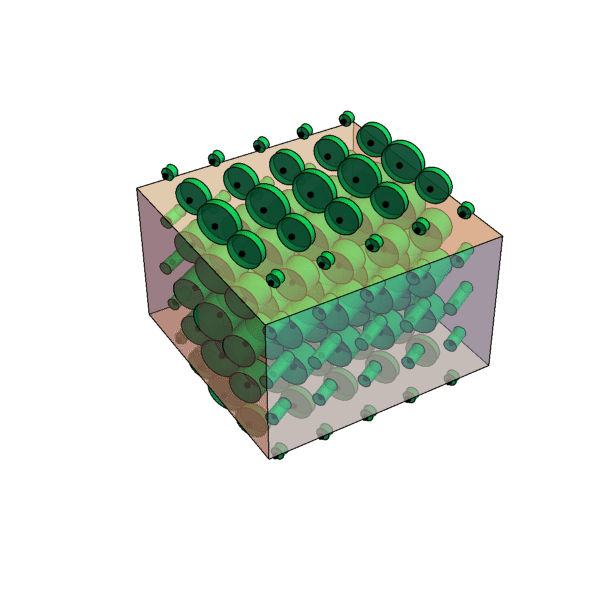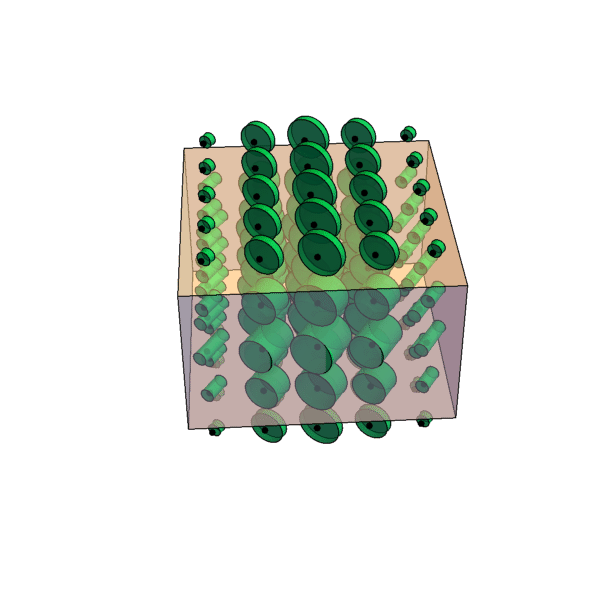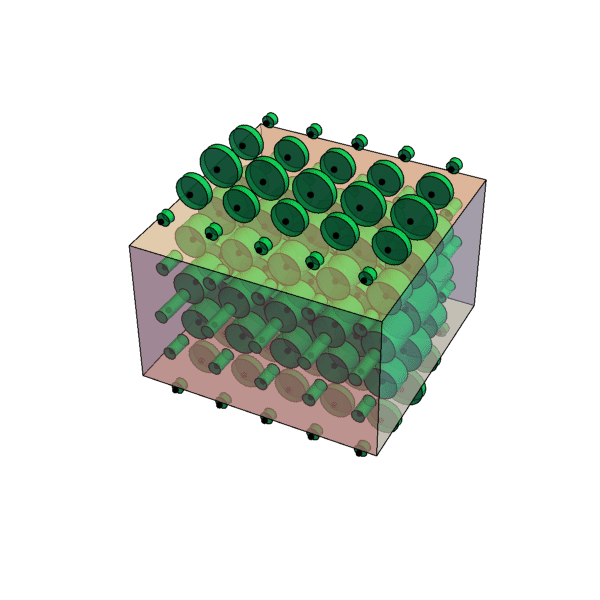In theory it works in any number of dimensions, but it works nearly as nice, if not nicer in 5D and 6D than in 4D and becomes a lot more complicated und confusing from 7D onwards. In 5D it's visually particulary clear, but conceptually it's not as beautiful as 6D. 6 is also a very interesting number of dimensions, so I'm going to explain it just refering to 6D.
The basic idea is that we can seperate hexaspace in two interrelated 3D sections.
One with the coordinates x, y and z. I'm gonna call this section XYZ. It's a function of u, v and w, as every combination of these coordinates gives a distinct section XYZ(u,v,w).
One with the coordinates u, v and w. I'm gonna call this section UVW. It's a function of x, y and z, as every combination of these coordinates gives a distinct section UVW(x,y,z).
If we consider an object in hexaspace its section in UVW will look like a 3D-object with its shape depending on x, y and z. We can visualize this relationship by placing the object's center in a point (x, y, z) in an outer coordinate system. We can then imagine it as an object that morphs its shape as it moves through XYZ. A bit more abstract, though more appropriate, we can imagine that every set (x, y, z) is associated with a shape in UVW.
The position of a dot inside the object is given by the coordinates u, v and w. If we fix a point in UVW and vary x, y and z, we keep our location inside the object, moving through XYZ. As the object looks different at any location and certainly it ends somewhere, there is a region, where the chosen point crosses the border of the object (it looks like the shape's border is moving, but it's actually the point moving in XYZ). We can draw the shape of this border in XYZ, which might look different for every combination of u, v and w - the location of the dot inside of the object in UVW.
To sum it up we have one object in UVW, which is given by the set of points that lie inside of the 6D-object for a given set (x, y, z) and another object XYZ, which is given by the set of points that lie inside of the 6D-object for a given set (u, v, w). The concept of an "inner" and an "outer" object is just a crutch for our imagination. In reality, and I think there lies the full beauty of the concept, both objects play equal roles and are exchangeable. The position of the dot inside the smaller object can as well be seen as the location of the larger object, with every point (u, v, w) having a different shape attributed to it. And this time we see why the shape changes with x,y and z which changes its shape with u, v and w and we've come full circle.
Here is an example. It's the carthesian product of a triangle prism and a sphere. The green cylinder is actually defined at every point inside the cuboid shape (and the black dot as well - it's in fact a volume), but is just drawn examplary at some points in order to show, how it relates to x, y and z. The cuboid shape marks the region where the black dot crosses the green cylinder, which is where the object ends in x-, y- and z-direction for a given set of (u, v, w). All the dots inside of the cuboid are also inside their cylinders. You can now mentally walk around in 6D by changing the position of one cylinder inside the cuboid (position in XYZ) and the position of the black dot (which is entangled with the cuboid) inside the cylinder (position in UVW) and test out the relations between the different coordinates. Don't worry, I'm planning to add some animations.


One more remark: It's a matter of taste, how to chose the subspaces. One could as well take XUW and YZV or any of the other 8 possible combinations. Every time it might look different. Appling rotations to the object would certainly help to comprehend relations between the two cross sections geometrically and vice versa.