[img]C:\Documents%20and%20Settings\Administrator\Desktop\Prashant\Higher%20Dimensions%20Database\3D%20Projection.htm[/img]
In this link, I have drawn a very imprecise figure of a 3D projection of two perpendicular cubes meeting at one of their faces. I have been recently trying to make use of projections to visualise 4D after I realised certain things. I realised that we infer 3D by the difference in shading of a 2D projection. I tried to visualise this particular dichoral angle by imagining the volume of the cubes coloured green, light near the faces and dark at the ends, analogous to the way we might see a dihedral angle between two squares projected on a plane. But as I start trying to infer the fourth dimension from this, I fail somewhere. Otherwise I should be seeing the squares on top to be perpendicular to each other.
3D projections
8 posts
• Page 1 of 1
3D projections
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: 3D projections
The link does not work
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: 3D projections
No big deal. Let's pull some pics you're looking for out of the internet:

The square within square projection of a 3D cube.
• This is a two dimensional shadow of the wireframe of a cube.
• It is a 2D model of a flattened 3D object
• There are two squares and four trapezoids
• The squares are parallel to Flatland
• The big square is closest, and the small square in the center is furthest from us into 3D
• The trapezoids are squares that extend away into 3D
• The 3D volume is contained in between the big and little square, and the trapezoids
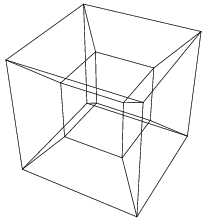
The cube within cube projection of a tesseract
• This is a three dimensional shadow of the wireframe of a teseract.
• It is a 3D model of a flattened 4D object
• There are two cubes and six trapezoid prisms
• The cubes are parallel to Realmspace
• The big cube is closest, and the small cube in the center is furthest from us into 4D
• The trapezoid prisms are cubes that extend away into 4D
• The 4D volume is contained in between the big and little cube, and the trapezoid prisms

The square within square projection of a 3D cube.
• This is a two dimensional shadow of the wireframe of a cube.
• It is a 2D model of a flattened 3D object
• There are two squares and four trapezoids
• The squares are parallel to Flatland
• The big square is closest, and the small square in the center is furthest from us into 3D
• The trapezoids are squares that extend away into 3D
• The 3D volume is contained in between the big and little square, and the trapezoids

The cube within cube projection of a tesseract
• This is a three dimensional shadow of the wireframe of a teseract.
• It is a 3D model of a flattened 4D object
• There are two cubes and six trapezoid prisms
• The cubes are parallel to Realmspace
• The big cube is closest, and the small cube in the center is furthest from us into 4D
• The trapezoid prisms are cubes that extend away into 4D
• The 4D volume is contained in between the big and little cube, and the trapezoid prisms
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D projections
What I was trying to post was actually something simpler than the whole tesseract itself: only one dichoral angle. I think that inferring 4D depth in a 3D projection of a simple dichoral angle should be the first thing to try in visualising 4D, because more complex 4D figures consist of this dichoral angle. It is as essential as a dihedral angle in 3D. So I thought it would be best for me to start imagining an unevenly shaded form of this:

I took this from a link of the face first projection of a tesseract, because two cells meeting at a face (ridge) of a tesseract was almost exactly what I wanted to visualise. The difficulty came with the necessity of having the interior shaded and coloured. Here we just have the ridges shaded transluscently. I want to start inferring 4D depth from this the way we infer 3D depth from this:

I have chosen the (n-2)-surtope first projection because they contain the simple angle between two (n-1)-surtopes meeting at an (n-1)-surtope.

I took this from a link of the face first projection of a tesseract, because two cells meeting at a face (ridge) of a tesseract was almost exactly what I wanted to visualise. The difficulty came with the necessity of having the interior shaded and coloured. Here we just have the ridges shaded transluscently. I want to start inferring 4D depth from this the way we infer 3D depth from this:

I have chosen the (n-2)-surtope first projection because they contain the simple angle between two (n-1)-surtopes meeting at an (n-1)-surtope.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: 3D projections
Another thing to consider, is how all the angles within a tesseract are all 90º right angles, where they only look different because of the projection. The n-1 cubes meet the n-2 squares at 90º , the n-2 squares meet the n-3 lines at 90º , and the n-3 lines meet the n-4 vertices at 90º. And, remember the neat animations of the tesseract, too! Combining a projection with passing though a 3-plane can make for a very thorough illustration of such things. I always encourage use of those explore functions, too, since you can change angles and depth of the viewing 3-plane to wherever you like, in real-time. Imagining our 3 dimensions as compressed as Flatland helps visually with what you see, in how the tesseract comes in from a higher direction, and completely passes through. 3D is just an extra positive/negative region that sticks away from Flatland, just as much as 4D is an extra +/- region from 3D.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D projections
Prashantkrishnan wrote:What I was trying to post was actually something simpler than the whole tesseract itself: only one dichoral angle. I think that inferring 4D depth in a 3D projection of a simple dichoral angle should be the first thing to try in visualising 4D, because more complex 4D figures consist of this dichoral angle. It is as essential as a dihedral angle in 3D. So I thought it would be best for me to start imagining an unevenly shaded form of this:
I took this from a link of the face first projection of a tesseract, because two cells meeting at a face (ridge) of a tesseract was almost exactly what I wanted to visualise. The difficulty came with the necessity of having the interior shaded and coloured. Here we just have the ridges shaded transluscently. I want to start inferring 4D depth from this the way we infer 3D depth from this:
I have chosen the (n-2)-surtope first projection because they contain the simple angle between two (n-1)-surtopes meeting at an (n-1)-surtope.
The thing about 4D visualization is that you can only adequately visualize 4D from a fully 3D projection. No image on the screen will ever suffice for this. The screen is 2D, and no amount of trickery is going to make it somehow 3D. The 3D doesn't exist on the screen; it only exists in our mind. The images on the screen are merely a "crutch" for us to reconstruct, in our mind's eye, the 3D model that is the real projection. The depth inference cannot happen from 2D images from the screen, because losing 2 dimensions is too much. You have to use the 2D images to construct a clear 3D model in your mind, and then infer 4D depth from the 3D mental model.
One of the main limitations of computer screen images is that you cannot "paint the inside" of the volumes, the same way you can paint the faces of a cube red and green, like in the above image. This is not possible on the computer screen because it is inherently 2D, so if you "paint" the inside of a cube, the paint on the surface of the cube will obscure the view of the paint inside the cube. No matter how you try it, you can never fully capture the full 3D volume inside the cube. There are ways of working around this when the texture inside the cube is simple enough -- e.g., for trivial patterns, you can use a 3D modeller to put fog inside the cube to show darker/lighter parts of the hypersurface under 4D illumination, but this approach only works for trivial textures. Past a certain level of complexity, you won't be able to represent it in a way that makes any sense -- it will just look like random clouds inside the cube with no discernible pattern.
So the only way is to construct the 3D image in your mind. Of course, this is extremely hard without any aids, so we use the 2D images to help guide our mental construction of the 3D image (so that we're sure we aren't imagining something totally inaccurate!). Perhaps we can use multiple images highlighting different parts of the projection in order for us to piece them together into a coherent mental picture of the full 3D projection. It's only when we construct a clear mental model of the 3D projection, that we can then infer 4D depth from it. It takes quite a lot of effort and concentration to do it, but it's totally worth it when you finally catch your first glimpse at what a 4D object looks like "from a native's eyes", as it were.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 3D projections
Another thing to note about 4D visualization, is that you have to stop thinking in terms of 2D areas, but you have to start thinking in terms of 3D volumes (i.e., 3D "hyper-area"). When you look at a 3D image of a cube, for example, you naturally don't pay very much attention to the edges of the cube. Your attention naturally focuses on the relations between the foreshortened images of the faces of the cube. Even when we perceive the 90° angle between the edges of the cube, it's only because of where they stand in relation to the faces of the cube. If you were to look at only the edges of the cube without the faces, the angles between them would be ambiguous -- this is the basis of the tumbling cube illusion.
Similarly, when you come to 4D, if you try to perceive the angle between two adjacent squares, you will find it very difficult. But it becomes much easier once you perceive in the context of the cubical facets of the tesseract. Once you can perceive the 90° angle between two adjacent cubes, then the 90° angle between the square faces will become clear.
Similarly, when you come to 4D, if you try to perceive the angle between two adjacent squares, you will find it very difficult. But it becomes much easier once you perceive in the context of the cubical facets of the tesseract. Once you can perceive the 90° angle between two adjacent cubes, then the 90° angle between the square faces will become clear.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: 3D projections
quickfur wrote:One of the main limitations of computer screen images is that you cannot "paint the inside" of the volumes, the same way you can paint the faces of a cube red and green, like in the above image. This is not possible on the computer screen because it is inherently 2D, so if you "paint" the inside of a cube, the paint on the surface of the cube will obscure the view of the paint inside the cube. No matter how you try it, you can never fully capture the full 3D volume inside the cube. There are ways of working around this when the texture inside the cube is simple enough -- e.g., for trivial patterns, you can use a 3D modeller to put fog inside the cube to show darker/lighter parts of the hypersurface under 4D illumination, but this approach only works for trivial textures. Past a certain level of complexity, you won't be able to represent it in a way that makes any sense -- it will just look like random clouds inside the cube with no discernible pattern.
This was one of the main issues why I once considered the set of segmentochora. Those have just one step into the fourth direction (the atop-height), and so everything is depictable by means of foreshortening.
 And still not everything is overcrowded. Those then are that easy to grasp that even 2D pics suffice in most cases, but interactive 3D images (e.g. VRML) surely work better.
And still not everything is overcrowded. Those then are that easy to grasp that even 2D pics suffice in most cases, but interactive 3D images (e.g. VRML) surely work better. --- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
8 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 3 guests
