How much time does it take to Visualize 4D?
22 posts
• Page 1 of 1
How much time does it take to Visualize 4D?
Though I understand this can be a bit early for me to ask questions like that, I want to know how much time does it approximately take to be able to have a basic visualization of the fourth dimension ?
I have been at it for slightly less than a week now but the only visualization that I have right now is - I visualize a 3D space and completely flatten it in my mind. Now I construct an axis (call it W) perpendicular to this plane-like surface and call this the fourth axis. How close is this to the real visualization?
I have been at it for slightly less than a week now but the only visualization that I have right now is - I visualize a 3D space and completely flatten it in my mind. Now I construct an axis (call it W) perpendicular to this plane-like surface and call this the fourth axis. How close is this to the real visualization?
- Ambar
- Nullonian
- Posts: 2
- Joined: Thu Mar 14, 2013 7:39 am
Re: How much time does it take to Visualize 4D?
There are several possibilities known to visualize 4D by 3D means. Yours is one of those. Not too bad one, after all.
Sure there are sectioning possibilities, like making the fourth dimension a time-line (i.e. not to become a minkowski space, just as a means of visualization!), that is, running through the sequence of sections in equitime steps, kind of a movie. - While that one allows to see just one section at a time, there is a different similar possibility, applicable to uncolored 4D things only: mapping the fourth dimension onto a colorspace, e.g. red would be closest, orange a bit farer off, then yellow, etc. Here you've the possibility to visualize all the depth at the same time. (Sure you will have to use semitransparent faces at least.)
Finally there is the mapping of the fourth dimension onto a scaling line. This applies only to unit-edged polytopes, as only then the visualy different sized edges can be recognized as being farer off resp. nearer according to their displayed size. This concept is esp. well-suited for the visualization of segmentochora (unit-edged polychora with vertices both on a hypersphere and on 2 parallel hyperplanes) as those 2 parallel base facets then are displayed concentrically, and the lacings as slightly distorted cells inbetween.
Sure that latter concept applies also beyond 2-layered unit-edged figures. But then the plentitude of concentrical layers and all those edges connecting these might become a mess. In those cases a stereo pair of 2D pictures of that 3D display of the the 4D figure might serve a good deal. (Cf. quickfur's pics.)
For duoprisms and related ones you further could use the toroidal display: the squares of a duoprism represent a tetragonal grid on a torus. The prisms then can be understood as sections at the inside, resp. orthogonal sections of the outside.
Finally you could become used with the representation by Dynkin symbols. This - as is - will be a versatile representation. Including the pure mechanics to read off therefrom the facets, the vertex figure, and this all the hierarchy down. But there even are possibilities to decompose that higher dimensional figure into stacks of vertex layers, and to describe either section by individual Dynkin symbols, providing thus a stack of Dynkin symbols (all having a common symmetry, orthogonal to the chosen axis). This is the concept of lace towers (not only applicable to 4D, but to any dimension!). You even might apply the same onto any of those layers again (using a common symmetry throughout), resulting in a lace city display.
--- rk
Sure there are sectioning possibilities, like making the fourth dimension a time-line (i.e. not to become a minkowski space, just as a means of visualization!), that is, running through the sequence of sections in equitime steps, kind of a movie. - While that one allows to see just one section at a time, there is a different similar possibility, applicable to uncolored 4D things only: mapping the fourth dimension onto a colorspace, e.g. red would be closest, orange a bit farer off, then yellow, etc. Here you've the possibility to visualize all the depth at the same time. (Sure you will have to use semitransparent faces at least.)
Finally there is the mapping of the fourth dimension onto a scaling line. This applies only to unit-edged polytopes, as only then the visualy different sized edges can be recognized as being farer off resp. nearer according to their displayed size. This concept is esp. well-suited for the visualization of segmentochora (unit-edged polychora with vertices both on a hypersphere and on 2 parallel hyperplanes) as those 2 parallel base facets then are displayed concentrically, and the lacings as slightly distorted cells inbetween.
Sure that latter concept applies also beyond 2-layered unit-edged figures. But then the plentitude of concentrical layers and all those edges connecting these might become a mess. In those cases a stereo pair of 2D pictures of that 3D display of the the 4D figure might serve a good deal. (Cf. quickfur's pics.)
For duoprisms and related ones you further could use the toroidal display: the squares of a duoprism represent a tetragonal grid on a torus. The prisms then can be understood as sections at the inside, resp. orthogonal sections of the outside.
Finally you could become used with the representation by Dynkin symbols. This - as is - will be a versatile representation. Including the pure mechanics to read off therefrom the facets, the vertex figure, and this all the hierarchy down. But there even are possibilities to decompose that higher dimensional figure into stacks of vertex layers, and to describe either section by individual Dynkin symbols, providing thus a stack of Dynkin symbols (all having a common symmetry, orthogonal to the chosen axis). This is the concept of lace towers (not only applicable to 4D, but to any dimension!). You even might apply the same onto any of those layers again (using a common symmetry throughout), resulting in a lace city display.
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: How much time does it take to Visualize 4D?
I see, I will look into the many new ways that you talked about. But you did not answer the original question - How long did it take you to visualize 4D in a basic sense?
- Ambar
- Nullonian
- Posts: 2
- Joined: Thu Mar 14, 2013 7:39 am
Re: How much time does it take to Visualize 4D?
I really suppose it's how much effort you put into it, and what you are expecting.
You could probably get significant results in six or so months, if you do it properly, maybe less.
Most of the terminology is written by mathematicians who don't often go out and have a look, so the 'common' meanings of words get skewered into less obvious meanings. All things, have a meaning in terms of a point (ie a fixed dimension), and against all space (a dimension N less than solid). A word like 'face' is of the latter (a facing wall prevents us from crossing it, must extend in a way that cuts a solid). You must keep this in mind when you try to fashion things in the higher dimensions.
The first thing to realise is that a 4d picture or map, is a thing of 3d, so you might suppose holographic vision, (ie imagine that you're looking into the interior of tomething), and still imagine that there's no 'in between'. This is like looking from the edge of a photo, and imagine that your ability to see past the edge is just a ruse to look from above.
The next step is to remember that things fall down in pictures but not in maps. So if your 3d image (which has gravity), is like holding a poster up in the air. You would imagine that if the picture has gravity, then things could fall down, but holding a map vertically does not mean that England is going to fall into France.
One must separate the dimensionality from a number. Much of the terminology that you find, supposes that things like faces and edges have a fixed dimension, while the common usage of these have a dimension that is related to solid space. A face prevents you from seeing through it in 3d and in 4d, so you might suppose the dimensionality of a bounding face increases to match solid space.
It's useful to think of space also as being 'divided' (ie reduced a dimension). So a map is a 4d scene divided by its hight. A picture is a 4d scene divided by its depth.
Some things are supprising. A knife cuts, because its sweep divides a solid. So, the dimensionality of the cutting edge, is solid space, divided by length (we only want a cut, not a squash), and the sweep of time. So it's two dimensions less than solid, not 'one dimensional'. You get to think of things, not just by dimension, but by its relation to solid space.
Some things keep their dimension: a bus route is a line in every dimension: go from A to B. But the shore-line is a division of the surface, ie solid space less two. In four dimensions you have a 2d shore. These are the sorts of things which i have tried to list in my polygloss, the sorts of things that greatly assist grasping four and higher dimensions.
The highest dimension i have managed in the main, is to look down the pencil of a vertex in 7d, and see the entirity of 6 dimensions down there.
'Lace cities', help. This is to plot the coordinates of a polytope not just by section, but over a 2d section. You can use the diagram to 'rotate' the thing in your mind, without loosing sight of how it falls. Lace cities are sections scattered over 2d, 'laced together' by missing edges. You see a lot of them in Richard Klitzing's posts.
On the other hand, real cities in 4D, don't have blocks. Streets (which form the blocks), have the function of both uniting (eg A to B). In 3d, a 1d thing is aslo N-2, so it makes a division of the surface into blocks. In four dimensions, the streets no longer divide, so one can have a town where there are no predestrian crossings, no bridges, etc. This is like the body, where there are no level crossings between blood streams, and the digestive system, and the breathing system. They are all lines, they all branch, but there are no 'blood-streem crossings' for the nervous system.
Time is not a good approach to 4d. If you count the 4d as time, then you reduce space-time to the sort of flip-images that kids are want to draw in the margin of books, to flick them to make animations. A stack of slightly different 2d pictures is no more 3d (it's 2d + time), as time is the 4D is. Nor are the sort of space diagrams with warps around balls to be seen as being the 4D. This has time, but the depth around the large masses are just a kind of billiard board table. The ball falls into the mass, because it falls in the hole - Earth in the side pocket, so to speak.
You could probably get significant results in six or so months, if you do it properly, maybe less.
Most of the terminology is written by mathematicians who don't often go out and have a look, so the 'common' meanings of words get skewered into less obvious meanings. All things, have a meaning in terms of a point (ie a fixed dimension), and against all space (a dimension N less than solid). A word like 'face' is of the latter (a facing wall prevents us from crossing it, must extend in a way that cuts a solid). You must keep this in mind when you try to fashion things in the higher dimensions.
The first thing to realise is that a 4d picture or map, is a thing of 3d, so you might suppose holographic vision, (ie imagine that you're looking into the interior of tomething), and still imagine that there's no 'in between'. This is like looking from the edge of a photo, and imagine that your ability to see past the edge is just a ruse to look from above.
The next step is to remember that things fall down in pictures but not in maps. So if your 3d image (which has gravity), is like holding a poster up in the air. You would imagine that if the picture has gravity, then things could fall down, but holding a map vertically does not mean that England is going to fall into France.
One must separate the dimensionality from a number. Much of the terminology that you find, supposes that things like faces and edges have a fixed dimension, while the common usage of these have a dimension that is related to solid space. A face prevents you from seeing through it in 3d and in 4d, so you might suppose the dimensionality of a bounding face increases to match solid space.
It's useful to think of space also as being 'divided' (ie reduced a dimension). So a map is a 4d scene divided by its hight. A picture is a 4d scene divided by its depth.
Some things are supprising. A knife cuts, because its sweep divides a solid. So, the dimensionality of the cutting edge, is solid space, divided by length (we only want a cut, not a squash), and the sweep of time. So it's two dimensions less than solid, not 'one dimensional'. You get to think of things, not just by dimension, but by its relation to solid space.
Some things keep their dimension: a bus route is a line in every dimension: go from A to B. But the shore-line is a division of the surface, ie solid space less two. In four dimensions you have a 2d shore. These are the sorts of things which i have tried to list in my polygloss, the sorts of things that greatly assist grasping four and higher dimensions.
The highest dimension i have managed in the main, is to look down the pencil of a vertex in 7d, and see the entirity of 6 dimensions down there.
'Lace cities', help. This is to plot the coordinates of a polytope not just by section, but over a 2d section. You can use the diagram to 'rotate' the thing in your mind, without loosing sight of how it falls. Lace cities are sections scattered over 2d, 'laced together' by missing edges. You see a lot of them in Richard Klitzing's posts.
On the other hand, real cities in 4D, don't have blocks. Streets (which form the blocks), have the function of both uniting (eg A to B). In 3d, a 1d thing is aslo N-2, so it makes a division of the surface into blocks. In four dimensions, the streets no longer divide, so one can have a town where there are no predestrian crossings, no bridges, etc. This is like the body, where there are no level crossings between blood streams, and the digestive system, and the breathing system. They are all lines, they all branch, but there are no 'blood-streem crossings' for the nervous system.
Time is not a good approach to 4d. If you count the 4d as time, then you reduce space-time to the sort of flip-images that kids are want to draw in the margin of books, to flick them to make animations. A stack of slightly different 2d pictures is no more 3d (it's 2d + time), as time is the 4D is. Nor are the sort of space diagrams with warps around balls to be seen as being the 4D. This has time, but the depth around the large masses are just a kind of billiard board table. The ball falls into the mass, because it falls in the hole - Earth in the side pocket, so to speak.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: How much time does it take to Visualize 4D?
Ambar wrote:I see, I will look into the many new ways that you talked about. But you did not answer the original question - How long did it take you to visualize 4D in a basic sense?
 Right you are.
Right you are. (This, in fact, was by purpose.)
Any those possibilities are mere crutches. There is no actual way to visualize 4D by mere 3D means. Therefore it cannot differ from a lifetime attempt.
And the slope of that exponetial learning-curve for sure depends on any individual:
- How hard you are willing to try.
- How frequently you are using either shown up way.
- Possibly trying different possibilities for the same polytope.
- Etc.
Me for one, I made my PHD in 1995. I started my IncMats website in about 2004. Meanwhile it contains individual files for nearly 900 different polychora, and a total of more than 2000 different polytopes (up to 10-D).

So you get a feeling on what is possible?
 Do not hesitate, just try!
Do not hesitate, just try! (You'll have my personal encouragement.)
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: How much time does it take to Visualize 4D?
It took me several months to get the basics down, and years after that to refine it.  I use the projection approach, the basic principles of which are described here.
I use the projection approach, the basic principles of which are described here.
 I use the projection approach, the basic principles of which are described here.
I use the projection approach, the basic principles of which are described here.- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: How much time does it take to Visualize 4D?
It took me several months as well with help from people here and some intense determination.
I now feel I can comfortably visualise 4D scenarios more accurately without making commonplace foobars anymore.
My personal experience is that it does take awhile to step away from all the traps of 3D to fully grasp the situation.
Your starting off to a good track by being able to state that our 3D world is flat to a 4Der.
Afterall our space is length x width x height x zero to them which is 0m4 of their space.
This is just the same as a 2Ders world is seen as flat to us - though they would not necessarily think of it that way; just as we don't for our world.
We see a square as length x width x zero which is 0m3 of our space; or in otherwords: flat.
I've been more keen to work out the natural settings of the various dimensional worlds.
I discovered that no matter how many dimensions you have there is still only one forward direction and one up direction relative to the 4Der and their theoretical planets.
That does simplify the whole concept a lot and makes it easier to imagine how things would grow in a four dimensional world.
Here's a little checklist for you to see how you are going so far:
1. Understand that a cube has two faces to a 4Der when they 'flip' it over and not 6 faces as we see them as we 'rotate' the cube.
2. Understand that a 4Ders retina is a 3D array of cones unlike our 2D array of cones.
3. Understand that it takes an infinite number of cubes to make a single tesseract (or hypercube).
4. Understand (from 3) that we could never draw enough cubes to represent even a single tesseract of any size.
5. Understand just how vast a 4D world is compared to ours.
6. Understand that there are no need for bridges to cross rivers.
7. Understand that there is no need for overpasses or underpasses for car ways.
8. Understand that there is no need for pedestrian crossings as we can just walk around the continuous side of the road.
How are you going so far with these?
I now feel I can comfortably visualise 4D scenarios more accurately without making commonplace foobars anymore.
My personal experience is that it does take awhile to step away from all the traps of 3D to fully grasp the situation.
Your starting off to a good track by being able to state that our 3D world is flat to a 4Der.
Afterall our space is length x width x height x zero to them which is 0m4 of their space.
This is just the same as a 2Ders world is seen as flat to us - though they would not necessarily think of it that way; just as we don't for our world.
We see a square as length x width x zero which is 0m3 of our space; or in otherwords: flat.
I've been more keen to work out the natural settings of the various dimensional worlds.
I discovered that no matter how many dimensions you have there is still only one forward direction and one up direction relative to the 4Der and their theoretical planets.
That does simplify the whole concept a lot and makes it easier to imagine how things would grow in a four dimensional world.
Here's a little checklist for you to see how you are going so far:
1. Understand that a cube has two faces to a 4Der when they 'flip' it over and not 6 faces as we see them as we 'rotate' the cube.
2. Understand that a 4Ders retina is a 3D array of cones unlike our 2D array of cones.
3. Understand that it takes an infinite number of cubes to make a single tesseract (or hypercube).
4. Understand (from 3) that we could never draw enough cubes to represent even a single tesseract of any size.
5. Understand just how vast a 4D world is compared to ours.
6. Understand that there are no need for bridges to cross rivers.
7. Understand that there is no need for overpasses or underpasses for car ways.
8. Understand that there is no need for pedestrian crossings as we can just walk around the continuous side of the road.
How are you going so far with these?
- gonegahgah
- Tetronian
- Posts: 490
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: How much time does it take to Visualize 4D?
gonegahgah wrote:... 3. Understand that it takes an infinite number of cubes to make a single tesseract (or hypercube). ...
Just as
- a line has 2 ends,
- a square has 4 sides,
- a cube has 6 faces,
- a tesseract will have 8 cubes!
In fact, each boundary facet of any arbitrary-dimensional hypercube will be orthogonal to one of the coordinate directions, one being placed at +1, one at -1 (if edge length would be 2 units).
Consider the following 2D net (folding device) for the 3D cube:
- Code: Select all
+--+
| |
+--+--+--+
| | | |
+--+--+--+
| |
+--+
| |
+--+
The respective net for the tesseract (to be cut from a 3D paper, and to be folded into 4D to encase the body of the tesseract) would then be:
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: How much time does it take to Visualize 4D?
Sorry, for the poorly expressed explanation.
Yes, 6 square faces will form a cube shell or empty cube,
and 8 cube faces will form a tesseract shell or empty tesseract.
What I meant to convery was that it takes an infinite number of cubes to make a solid tesseract.
This is the same as it takes an infinite number of 2D squares to make a solid 3D cube.
Hope that is better explained?
Yes, 6 square faces will form a cube shell or empty cube,
and 8 cube faces will form a tesseract shell or empty tesseract.
What I meant to convery was that it takes an infinite number of cubes to make a solid tesseract.
This is the same as it takes an infinite number of 2D squares to make a solid 3D cube.
Hope that is better explained?
- gonegahgah
- Tetronian
- Posts: 490
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: How much time does it take to Visualize 4D?
Got it.
So "an infinite number" implies somehow a numerable infinitude, while that what you've got in mind, clearly makes up a continuum, i.e. a non-numerable infinitude.
--- rk
So "an infinite number" implies somehow a numerable infinitude, while that what you've got in mind, clearly makes up a continuum, i.e. a non-numerable infinitude.
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: How much time does it take to Visualize 4D?
There is a good deal of disagreement here, as to whether a cube is made of squares in the manner a book is made of pages.
While one can sample a cube at a great variety of positions and get squares, it is not made of them. There are points on the height that are never able to be constructed, and thus never samplable.
But if you want to think of constructions in terms of rice-paper constructions, or constructions like MRI (magnetic resonance imaging = slice images of the body), then yes, the cube can be made of sampled squares. It gets there, but not the way to look at it, since we don't normally look at things by sampled plane sections.
While one can sample a cube at a great variety of positions and get squares, it is not made of them. There are points on the height that are never able to be constructed, and thus never samplable.
But if you want to think of constructions in terms of rice-paper constructions, or constructions like MRI (magnetic resonance imaging = slice images of the body), then yes, the cube can be made of sampled squares. It gets there, but not the way to look at it, since we don't normally look at things by sampled plane sections.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: How much time does it take to Visualize 4D?
Hi Wendy. I wouldn't say so much disagreement; but clarification.
Science is loathe of 'infinite' (infinitely big or infinitely small) even eskewing continuity by setting a plank limit on smallness.
Though it would appear, even if at first reluctantly; but now fully embraced, it uses the cancellation out of infinities when it is convenient...
But, whether we try to fit our Universe to our math as our science is attempting, it still remains that it is possible to conceive of an infinite number of points between two points.
So it becomes a debate of whether our math/science can represent the Universe or not.
In the same respect I find it possible to conceive of an infinite number of conceptual 2D squares side by side that will eventually form a cube.
We already suspend some scientific 'fact' in these forums by the very nature of discussing spatial 4D space so I don't think we need to be as rigourous in exclusion of infinity.
Of course, no physical object occupies a square area of uninterrupted continuity but that does not disallow us to conceive it.
And so it goes for conceiving the squares side by side to form a cube.
Each added square moves the growing base ever closer to completing the cube but each added square also only progresses us an infinitely small amount.
I do believe, even thought the squares have 0 depth that each additional conceptual square does reside beside the previous square in line.
So, although they are all 0 depth they don't occupy the same depth point and excruciatingly slowly - taking forever literally - build toward completing the cube.
But these are all just diversions from the real concept at play here.
That is that any of our representations of tesseracts are purely 0 thin and can not convey the true bulk of a tesseract; ever.
It is easy to look at our drawing of a tesseract and think that it is a drawing of a real one but when the depiction disguises the bulk it fails to be true.
It is important, I believe, to have a sense of the extra space that is denied to us when we attempt to depict higher dimensional objects.
Until we can actually lift things into the extra dimension(s) we can never truly gauge their actual size except as a mathematical abstraction.
So, that is why I like to explain that we could build a billion or a trillion, or a googleplex of giant cubes and still not represent the bulk of the tiniest tesseract.
Not even of their atoms with their vast spaces in between. We couldn't even represent that even tinier amount!
It is a comforting thought I believe and one that gives pause...
I guess my answer to the OP question then is that none of us will ever truly visualise a higher dimensional object until we are able to raise ourselves into the extra dimension.
And that may be possible, as already mentioned, given enough time and ingenuity as we make advancements in interacting with the human brain.
Afterall, we already deal with our world at a pixel level. Even though we don't notice it, our vision has a resolution, and it is our brain that makes our vision appear continuous.
But we can make headway in conceiving what it must be like. I don't believe any of us here can say that we know exactly how a 4D world would settle out in its entirety.
We conjecture, based upon our math conceived from within this world, but it is difficult to truly model the results of living in a 4D space from our 3D viewpoint.
We can only propose what it might be like based upon what we do know and can progressively infer.
Hi Klitzing. That's it; pretty much what you said. I'm pretty sure I agree with your statement.
Science is loathe of 'infinite' (infinitely big or infinitely small) even eskewing continuity by setting a plank limit on smallness.
Though it would appear, even if at first reluctantly; but now fully embraced, it uses the cancellation out of infinities when it is convenient...
But, whether we try to fit our Universe to our math as our science is attempting, it still remains that it is possible to conceive of an infinite number of points between two points.
So it becomes a debate of whether our math/science can represent the Universe or not.
In the same respect I find it possible to conceive of an infinite number of conceptual 2D squares side by side that will eventually form a cube.
We already suspend some scientific 'fact' in these forums by the very nature of discussing spatial 4D space so I don't think we need to be as rigourous in exclusion of infinity.
Of course, no physical object occupies a square area of uninterrupted continuity but that does not disallow us to conceive it.
And so it goes for conceiving the squares side by side to form a cube.
Each added square moves the growing base ever closer to completing the cube but each added square also only progresses us an infinitely small amount.
I do believe, even thought the squares have 0 depth that each additional conceptual square does reside beside the previous square in line.
So, although they are all 0 depth they don't occupy the same depth point and excruciatingly slowly - taking forever literally - build toward completing the cube.
But these are all just diversions from the real concept at play here.
That is that any of our representations of tesseracts are purely 0 thin and can not convey the true bulk of a tesseract; ever.
It is easy to look at our drawing of a tesseract and think that it is a drawing of a real one but when the depiction disguises the bulk it fails to be true.
It is important, I believe, to have a sense of the extra space that is denied to us when we attempt to depict higher dimensional objects.
Until we can actually lift things into the extra dimension(s) we can never truly gauge their actual size except as a mathematical abstraction.
So, that is why I like to explain that we could build a billion or a trillion, or a googleplex of giant cubes and still not represent the bulk of the tiniest tesseract.
Not even of their atoms with their vast spaces in between. We couldn't even represent that even tinier amount!
It is a comforting thought I believe and one that gives pause...
I guess my answer to the OP question then is that none of us will ever truly visualise a higher dimensional object until we are able to raise ourselves into the extra dimension.
And that may be possible, as already mentioned, given enough time and ingenuity as we make advancements in interacting with the human brain.
Afterall, we already deal with our world at a pixel level. Even though we don't notice it, our vision has a resolution, and it is our brain that makes our vision appear continuous.
But we can make headway in conceiving what it must be like. I don't believe any of us here can say that we know exactly how a 4D world would settle out in its entirety.
We conjecture, based upon our math conceived from within this world, but it is difficult to truly model the results of living in a 4D space from our 3D viewpoint.
We can only propose what it might be like based upon what we do know and can progressively infer.
Hi Klitzing. That's it; pretty much what you said. I'm pretty sure I agree with your statement.
- gonegahgah
- Tetronian
- Posts: 490
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: How much time does it take to Visualize 4D?
The issue is not so much that one can make a cube from thin squares, but that this is not a normal view even in three dimensions. We don't suppose that figures are comprised of sections, but rather projections.
So looking at the sort of things that quickfur does is a better model of four dimensions, especially if one supposes that foreshortening is as normal in views of 4d, as it is of 3d. Some foreshortening can result in a loss of dimension completely.
W
So looking at the sort of things that quickfur does is a better model of four dimensions, especially if one supposes that foreshortening is as normal in views of 4d, as it is of 3d. Some foreshortening can result in a loss of dimension completely.
W
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: How much time does it take to Visualize 4D?
Well, somewhere the additional dimension has to go, for sure, when visualizing 4D by 3D means.
One way, as mentioned by me as one of the possibilities, and now second by gonegahgah, would be using a stack of sections, i.e. kind a slicing movie. - Even so this is a valid representation, I agree with Wendy, that it usually (i.e. outside of mere prisms, or more generally: any segmentochora) is not the best way to "see" the to be seen structures.
A different way would be to switch from cartesian coordinate display onto polar coordinate display, i.e. to scale the additional dimension down as concentric, increasingly scaled - well, sections again. - This comes out to be nothing but the projection of the 4D structure onto a 3D screen, from a finite point of view. - This is most probably what Wendy bears in mind here.
Alternatively you could consider to map more or less hyperspherical structures (as most polychora of considerations are) onto that hypersphere itself, and finally either map each half of that hypersphere onto flat 3D space - or pinch a little hole somewhere and pull that out onto infinity of either direction (kind of distorting the gum skin of a baloon into flat space).
I for one would not be as harsh as Wendy. Any of those means are valid representations. (Others were provided already in a privious mail of mine.) It is rather the ease of to be derived conclusions that makes either one more or less valuable. - Best for sure, when supported within a different display as well.
So, I'd recommend, try into either direction, get aquainted with either visualization, and then choose, what will serve you most (in any specific case). - Most probably there will be different means best for different purposes.
Whereas to choose first one specific way of representation as a single approach will not only make several things much harder, it even might lead to wrong conclusions.
--- rk
One way, as mentioned by me as one of the possibilities, and now second by gonegahgah, would be using a stack of sections, i.e. kind a slicing movie. - Even so this is a valid representation, I agree with Wendy, that it usually (i.e. outside of mere prisms, or more generally: any segmentochora) is not the best way to "see" the to be seen structures.
A different way would be to switch from cartesian coordinate display onto polar coordinate display, i.e. to scale the additional dimension down as concentric, increasingly scaled - well, sections again. - This comes out to be nothing but the projection of the 4D structure onto a 3D screen, from a finite point of view. - This is most probably what Wendy bears in mind here.
Alternatively you could consider to map more or less hyperspherical structures (as most polychora of considerations are) onto that hypersphere itself, and finally either map each half of that hypersphere onto flat 3D space - or pinch a little hole somewhere and pull that out onto infinity of either direction (kind of distorting the gum skin of a baloon into flat space).
I for one would not be as harsh as Wendy. Any of those means are valid representations. (Others were provided already in a privious mail of mine.) It is rather the ease of to be derived conclusions that makes either one more or less valuable. - Best for sure, when supported within a different display as well.
So, I'd recommend, try into either direction, get aquainted with either visualization, and then choose, what will serve you most (in any specific case). - Most probably there will be different means best for different purposes.
Whereas to choose first one specific way of representation as a single approach will not only make several things much harder, it even might lead to wrong conclusions.
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: How much time does it take to Visualize 4D?
On my website, I discuss the weaknesses of the cross-sections method.
Nevertheless, in spite of the weaknesses of the approach, I have found that cross-sectioning polytopes is a very useful way of discovering, for example, CRFs, or for realizing just how much 4D bulk ("hypervolume") is present in a 4D object. The method is not as useful when you're interested in the surface topology, but it's quite handy when you're trying to find CRFs or do piece-wise construction of 4D objects (e.g. gluing parts together to make a bigger object).
I still argue, though, that perspective projection from a distance (i.e., not a Schlegel diagram) is probably the most "intuitive" approach to 4D visualization. I know some people here disagree with me , but it is the closest analogue to how our own eyes work in 3D, so a lot of useful dimensional analogies can be drawn from it.
, but it is the closest analogue to how our own eyes work in 3D, so a lot of useful dimensional analogies can be drawn from it.
Of course, as Klitzing points out, you can't just blindly trust a single method to do everything, because projection has its own weaknesses too, like illusions (which also happen in 3D -- see, for example, the mask illusion that's quite common in museums, in which the actual direction of rotation is contrary to what one perceives, because of deceptive lighting). One also has to understand what one is looking at -- in 3D, we have the benefit of instinctive 3D perception, but when dealing with 4D perception, we have to consciously re-interpret the image as a 4D projection. Otherwise, one falls into the trap of conflating the 3D projection with the 4D object itself, and fails to "put the 4D into the picture", as wendy puts it (i.e., the photograph of a person is not the person himself, but a projected representation of him; one should not draw the false conclusion that the person is flat just because the photograph is 2D -- one needs to "put the 3D" into the picture in order to have an accurate understanding of what it represents).
So 4D visualization really requires the selection of a most comfortable primary method (in my case, it's using perspective projection at-a-distance, or sometimes parallel projection if you want to analyze the exact structure -- analogous to what they use in engineering diagrams), backed up by a lot of cross-checking with other methods and mathematical verification. The latter is very important in order to not get misled; sometimes one may imagine a certain 4D object exists, but actual calculation shows that it can't (e.g., some time ago somebody thought they found a certain vertex figure in 4D, but actual calculation showed that one of the tetrahedra can't exist because some edge lengths have no solution in the real numbers). One always has to be cautious about jumping to conclusions, because we're not born with an intuitive grasp of 4D, and our 3D-centric bias tends to mislead us quite often.
Nevertheless, in spite of the weaknesses of the approach, I have found that cross-sectioning polytopes is a very useful way of discovering, for example, CRFs, or for realizing just how much 4D bulk ("hypervolume") is present in a 4D object. The method is not as useful when you're interested in the surface topology, but it's quite handy when you're trying to find CRFs or do piece-wise construction of 4D objects (e.g. gluing parts together to make a bigger object).
I still argue, though, that perspective projection from a distance (i.e., not a Schlegel diagram) is probably the most "intuitive" approach to 4D visualization. I know some people here disagree with me
 , but it is the closest analogue to how our own eyes work in 3D, so a lot of useful dimensional analogies can be drawn from it.
, but it is the closest analogue to how our own eyes work in 3D, so a lot of useful dimensional analogies can be drawn from it.Of course, as Klitzing points out, you can't just blindly trust a single method to do everything, because projection has its own weaknesses too, like illusions (which also happen in 3D -- see, for example, the mask illusion that's quite common in museums, in which the actual direction of rotation is contrary to what one perceives, because of deceptive lighting). One also has to understand what one is looking at -- in 3D, we have the benefit of instinctive 3D perception, but when dealing with 4D perception, we have to consciously re-interpret the image as a 4D projection. Otherwise, one falls into the trap of conflating the 3D projection with the 4D object itself, and fails to "put the 4D into the picture", as wendy puts it (i.e., the photograph of a person is not the person himself, but a projected representation of him; one should not draw the false conclusion that the person is flat just because the photograph is 2D -- one needs to "put the 3D" into the picture in order to have an accurate understanding of what it represents).
So 4D visualization really requires the selection of a most comfortable primary method (in my case, it's using perspective projection at-a-distance, or sometimes parallel projection if you want to analyze the exact structure -- analogous to what they use in engineering diagrams), backed up by a lot of cross-checking with other methods and mathematical verification. The latter is very important in order to not get misled; sometimes one may imagine a certain 4D object exists, but actual calculation shows that it can't (e.g., some time ago somebody thought they found a certain vertex figure in 4D, but actual calculation showed that one of the tetrahedra can't exist because some edge lengths have no solution in the real numbers). One always has to be cautious about jumping to conclusions, because we're not born with an intuitive grasp of 4D, and our 3D-centric bias tends to mislead us quite often.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: How much time does it take to Visualize 4D?
For me the initial trouble I had with multiple 3D slices of 4D objects was that I was trying to rotate the 3D slices alone or the parts of the 4D object as they were in the 3D slices.
The truth is that the 4D objects can rotate through any 3D slices we might make changing the composition of the slice.
So slices can be a trap to understanding 4D even if they are also a little help.
If we take a simple object like a 3D plusplus made of cylinders.
The following gives the idea but with cylinders instead of square prisms.

We could take this 3D object (making it of 3 perpendicular cylinders) and put it into the 2Der world.
They will see, from the front, two intersecting rectangles; one vertical the other forward-back.
If we rotate the object round the vertical axis they see the upright axis stay the same shape but the front-back rectangle lengthens+narrows but then shortens rapidly while narrowing.
It disappears before it seems to reappear in reverse though it is actually the left-right axis now coming into front-back view.
If we were to make the centre axis a barberpole the 2Der would see the red-white alternating line move downwards (or upwards).
If we had a 4D plus object with poles along all 4 perpendicular axis we would see something similar except that we could now just rotate through the sideways for example.
In this case the up-down pole and the forward-back poles would retain their shape while the 4D plus rotates through the sideways.
If the front-back pole and vertical pole were painted with a pattern in 4D we would see the pattern morphing on the poles as they were rotated through the sideways.
This is really cool.
The truth is that the 4D objects can rotate through any 3D slices we might make changing the composition of the slice.
So slices can be a trap to understanding 4D even if they are also a little help.
If we take a simple object like a 3D plusplus made of cylinders.
The following gives the idea but with cylinders instead of square prisms.
We could take this 3D object (making it of 3 perpendicular cylinders) and put it into the 2Der world.
They will see, from the front, two intersecting rectangles; one vertical the other forward-back.
If we rotate the object round the vertical axis they see the upright axis stay the same shape but the front-back rectangle lengthens+narrows but then shortens rapidly while narrowing.
It disappears before it seems to reappear in reverse though it is actually the left-right axis now coming into front-back view.
If we were to make the centre axis a barberpole the 2Der would see the red-white alternating line move downwards (or upwards).
If we had a 4D plus object with poles along all 4 perpendicular axis we would see something similar except that we could now just rotate through the sideways for example.
In this case the up-down pole and the forward-back poles would retain their shape while the 4D plus rotates through the sideways.
If the front-back pole and vertical pole were painted with a pattern in 4D we would see the pattern morphing on the poles as they were rotated through the sideways.
This is really cool.
- gonegahgah
- Tetronian
- Posts: 490
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: How much time does it take to Visualize 4D?
Even by all the methods that we try to visualise the fourth dimension, will our brains actually adapt to it? It has been an year and a half since I started learning the concepts about the fourth dimension, but I managed to register here only tonight. I am nowhere near visualising a duocylinder or a glome - these are the most difficult rotatopes for me.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: How much time does it take to Visualize 4D?
Prashantkrishnan wrote:Even by all the methods that we try to visualise the fourth dimension, will our brains actually adapt to it? It has been an year and a half since I started learning the concepts about the fourth dimension, but I managed to register here only tonight. I am nowhere near visualising a duocylinder or a glome - these are the most difficult rotatopes for me.
I couldn't visualize a duocylinder for a long time -- the mathematical descriptions of it were not helpful to me -- until I "accidentally" re-discovered it as the limiting shape of duoprisms. Of course, I had a hard time visualizing duoprisms until I "accidentally" re-discovered them by noticing certain features about the tesseract.
Consider the following usual projection of a tesseract into 3D space:

There are 8 cells depicted here: the outer cube, the inner cube, and 6 flat frustums that connect the outer cube to the inner cube. Of course, in 4D these are actually all regular cubes; the frustums only appear that way because of perspective distortion (just like looking at a square edge-on makes it appear as a thin trapezoid).
First, notice that 4 of the flat frustums form a 4-membered ring: take the front, back, left, and right frustums, and you see that they are cubes joined to each other by their opposite faces, and bent around the vertical axis to form a ring. The remaining cells then, form a second ring: the inner cube is connected to the top frustum, the top frustum is connected to the outer cube, the outer cube is connected to the bottom frustum, and the bottom frustum connects back to the inner cube. The trick here is to notice that this second ring is actually exactly the same as the first ring: each cube is connected to its neighbours by opposite faces. Of course, here the ring appears to be very different, but that's actually just an artifact of the projection. In 4D space, these two rings of cubes are actually exactly the same shape. Thus, the tesseract's surface can be cut into two rings of 4 cubes each.
Now begins the fun part. Suppose we ignore the second ring for the moment, and look at the first (horizontal) ring. That is, the front/back, left/right frustums. What happens if we insert a 5th cube into this ring? It would become a ring of 5 cubes (which would appear, in projection, as 5 frustums), which we can adjust the angles of, so that they form a pentagonal ring. The original second ring would no longer fit in with this ring, of course, because now the "hole" in this ring is pentagonal, whereas the cells of the second ring are cubes. But a simple modification makes the two rings fit together once more: by changing the cubes of the second ring into pentagonal prisms! So then we now have the 1st ring consisting of 5 cubes, and the second ring consisting of 4 pentagonal prisms, and these two rings will now close up in 4D to make ... the 5,4-duoprism.


Now suppose instead of having just 4 pentagonal prisms in the second ring, we have 6 pentagonal prisms? Well, then the 5 cubes of the first ring would no longer fit into the second ring. But again, another simple modification fixes this: just replace the 5 cubes with 5 hexagonal prisms. Thus, we have a ring of 5 hexagonal prisms and a second ring of 6 pentagonal prisms. These rings will now close up to form a closed 4D shape, that we call a 5,6-duoprism:

You probably noticed a pattern here. Given a ring of n-gonal prisms and another ring of m-gonal prisms, if there are m prisms in the first ring and n prisms in the second ring, they will close up into an m,n-duoprism. This construction works for any m≥3 and n≥3. It just so happens that when m=n=4, we get a tesseract. For all other values, we get various duoprisms.
Of course, it may not be immediately obvious that the above construction of duoprisms is equivalent to taking the Cartesian product of two polygons, but some careful study of the matter, which I'll leave as an exercise for the reader, should settle this.
So now we know how to visualize duoprisms. Let's take things one step further. Nobody says m and n are restricted to finite numbers. For example, we can construct an m,∞-duoprism by constructing m,n-duoprisms for larger and larger values of n, and then take the limit as n approaches infinity. So we get the following sequence of duoprisms (taking m=4 as an example case):


 ...
...As n approaches infinity, then, the n-gonal prisms in the vertical ring of the m,n-duoprisms become closer and closer to cylinders. At the same time, the cubes of the horizontal ring become flatter and flatter -- at the limit, then, the vertical ring becomes a ring of 4 cylinders, and the cubes of the horizontal ring become a torus with a square cross-section. This 4,∞-duoprism, it turns out, is none other than the cubinder:

But we aren't restricted to m=4. The following, for example, shows the case of m=6 (with a slightly rotated 4D viewpoint so that the vertical/horizontal rings are interchanged, but this is just a simple rotation in 4D):

These fascinating new shapes that have cylinders as cells are none other than the Cartesian products of a circle with various polygons.
By now, it should be obvious that there's no reason we restrict m to finite values; let's see what happens when m also approaches infinity:


 ...
...As you can see, as m increases, the cross-section of the torus becomes a higher and higher polygon that approximate a circle; while the cylinders in the ring of cylinders become flatter and flatter, and approach an infinitely flat disk. At the limit, an interesting thing happens: the torus becomes circular torus, and the ring of cylinders also become a circular torus. The two rings of the m,n,duoprisms have therefore converged into two interlocking tori:

This, we call a duocylinder.
 It's none other than the Cartesian product of two circles. The two tori are identical to each other; they only appear different in the above image because they're being seen from different angles in 4D. A simple 4D rotation would transform them into each other.
It's none other than the Cartesian product of two circles. The two tori are identical to each other; they only appear different in the above image because they're being seen from different angles in 4D. A simple 4D rotation would transform them into each other.- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: How much time does it take to Visualize 4D?
Now, visualizing a glome... that's a little more tricky, because a glome is completely smooth, with no features that might help you discern its shape, unlike shapes like the duocylinder where there's at least a ridge (a 2-manifold) that you can discern in projection images.
There are two ways to visualize a glome. One is by analogy with the difference between the appearance of a cylinder, viewed from one of its ends, and a sphere. Both appear as a circle (well, a disk, to be precise) in the 2D projection image that forms in our retina. How then do we tell the difference? We tell the difference by the difference in lighting, which tells us that one is flat, whereas the other "bulges" in its center. This "bulge" is what makes a sphere a sphere; if it didn't bulge, it'd just be a flat disk, even though both a disk (or the cap of a cylinder) appear as a circle in our eyes, the sphere reflects light differently due to its "bulge".
Now let's talk about the glome. If you look at one end of a spherinder in 4D, it will have a spherical projection image, and if you look at a glome in 4D, it will also have a spherical projection image. How do you tell the difference? Well, the spherinder cap doesn't "bulge"... that is, it has a spherical boundary, but the inside of the spherical boundary is a "flat" 3D volume. But the image of a glome, even though it also has a spherical boundary, has an inside volume that "bulges" outward in the 4th direction. The glome reflects light differently from a flat spherical hypersurface, so the spherinder's cap looks "flat", whereas the image of the glome "bulges outward" in the middle. That's how you know one is just a spherinder cap (or a regular 3D sphere), whereas the other is a glome.
The second method is by the Earth analogy: add some features to the featureless sphere by drawing longitude/latitude lines. This subdivides the surface of the earth into square-ish regions. In 4D, there are also analogous ways of subdividing the glome into approximately cubic regions. So by looking at the density distributions of these "longitude/latitude lines", you can get some idea about how the glome curves in 4D space. You can find more details about this on the wiki page.
There are two ways to visualize a glome. One is by analogy with the difference between the appearance of a cylinder, viewed from one of its ends, and a sphere. Both appear as a circle (well, a disk, to be precise) in the 2D projection image that forms in our retina. How then do we tell the difference? We tell the difference by the difference in lighting, which tells us that one is flat, whereas the other "bulges" in its center. This "bulge" is what makes a sphere a sphere; if it didn't bulge, it'd just be a flat disk, even though both a disk (or the cap of a cylinder) appear as a circle in our eyes, the sphere reflects light differently due to its "bulge".
Now let's talk about the glome. If you look at one end of a spherinder in 4D, it will have a spherical projection image, and if you look at a glome in 4D, it will also have a spherical projection image. How do you tell the difference? Well, the spherinder cap doesn't "bulge"... that is, it has a spherical boundary, but the inside of the spherical boundary is a "flat" 3D volume. But the image of a glome, even though it also has a spherical boundary, has an inside volume that "bulges" outward in the 4th direction. The glome reflects light differently from a flat spherical hypersurface, so the spherinder's cap looks "flat", whereas the image of the glome "bulges outward" in the middle. That's how you know one is just a spherinder cap (or a regular 3D sphere), whereas the other is a glome.
The second method is by the Earth analogy: add some features to the featureless sphere by drawing longitude/latitude lines. This subdivides the surface of the earth into square-ish regions. In 4D, there are also analogous ways of subdividing the glome into approximately cubic regions. So by looking at the density distributions of these "longitude/latitude lines", you can get some idea about how the glome curves in 4D space. You can find more details about this on the wiki page.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: How much time does it take to Visualize 4D?
I can understand the logic in the diagrams given by quickfur. I understand the reasoning about the ridges being easier to visualise in projections. I have seen many diagrams in the past two years, but none of then have helped my brain adapt to the fact that there can be four mutually perpendicular lines. Can you actually visualise that? Is that possible for 3D people like us?
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: How much time does it take to Visualize 4D?
When you draw a 3D graph on a 2D piece of paper, what do you do?
Probably something like this, right?
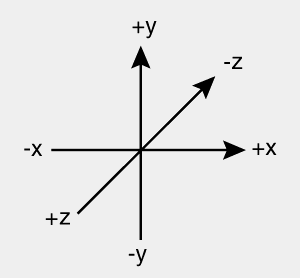
Congratulations - you have just projected 3 perpendicular axes into 2D, where they are not perpendicular any more!
You can imagine the w dimension being a fourth arrow on that diagram, and it can point in any direction you like (x, y and z could point in any direction you like as well). Now you have 4D projected into 2D.
You can add as many arrows as you like, if you want even higher dimensions.
Probably something like this, right?

Congratulations - you have just projected 3 perpendicular axes into 2D, where they are not perpendicular any more!
You can imagine the w dimension being a fourth arrow on that diagram, and it can point in any direction you like (x, y and z could point in any direction you like as well). Now you have 4D projected into 2D.
You can add as many arrows as you like, if you want even higher dimensions.

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: How much time does it take to Visualize 4D?
Sometimes I use time to visualize the 4th dimension. Sometimes I visualize the 4th dimension by having things closer to me in the 4th dimension a different shade than things further from me. Sometimes I try to visualize the 4th dimension by having the things closer to me in the 4th dimension more in focus than things further away from me. Sometimes I visualize the 4th dimension by having things in one direction on the inside and things in the other towards the outside. I can visualize the 4th dimension but it takes tremendous concentration for me to visualize it. I haven't tried visualizing in 5d. I have also tried using math to try to understand the 4th dimension.
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
- anderscolingustafson
- Tetronian
- Posts: 316
- Joined: Mon Mar 22, 2010 6:39 pm
22 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 22 guests
