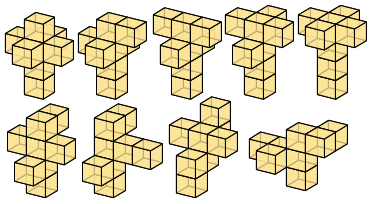
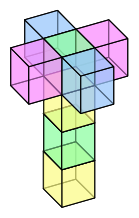
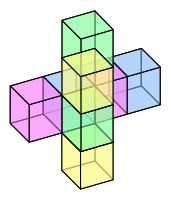
I’ve been looking at this picture of a tesseract, and I wondered if there an error on it. Since everything from 2D is proportional to 3D just as 3 D is proportional to 4D,
If we open up a square, we get 4 lines:

If we open up a cube, we get four squares in a line and two squares sticking out:

So if we open up a 4-cube, shouldn’t we get one with 6 cubes in a line, and two cubes sticking out like this:?

or this?

I dont see why a tesseract opened up would look almostl ike a cube opened up, when a square opened up (a line) is completely different than a cube opened up
p.s. sry if the pics are small, just click on them if u cant see it
[/url]