
Actually i'm working on my thesis work in the university, about computer graphics and the title is the same of this post.
Ok, the intention of my message is to make you know what i traying to do in my thesis and i hope you can tell me some recomendations or suggestions.
Specially i hope, you can tell me any direct aplication where n-dimensional rotations can be used.
Thanks a lot.

If you understand spanish, here is the Formal Proposal of my thesis.
http://irvingcm.googlepages.com/propuestaFormal.htm
And here, i'll write a small abstract:
Problem definition
There isn’t a generalization of the transformation equations that permit rotating n-dimensional objects, not only around the principal hyperplanes, but around a arbitrary hyperplane.
If we want to visualize the phenomena in nD (n>3), it’s necessary also, to generalize the projections equations (parallels and perspectives) that permit carrying the information in nD to 2D, by means of successive projections, in order to visualize it on a computer monitor.
The wire model of polytopes can be drawn from their vertexes, and we can know how to obtain that information, though, the order in which the vertexes should be drawn, is a process still not automatized, for example, to draw a 4D hypercube, we need to draw its 32 edges, the question is: In what order? This is another point to analyze, because it’ll be useful for automatically generating and drawing nD polytopes and placing them in the hyperspace.
General objective
The main goal of this research is to find the principal rotations in nD, to simulate the rotations of nD polytops around a general hyperplane, and finally show the result through projections in a computer monitor.
Specific objectives
• Definition of the projection equations to 2D, which permit visualizing the rotations from different points in the 4D space.
• Analysis and study nD,(n-1)D, …. 3D, 2D projections.
• Generalization of rotations and projections for nD polytopes.
• Definition of the general matrixes, called GO and BACK (necessary matrixes to carry an nD object to the origin, make the rotations, and take back the object to its original position.)
• Automatic generation of coordinates and draw of edges for nD regular polytops.
• Development of a multidimensional navigator.





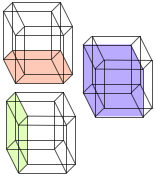

 ... or is a work about it exist ?
... or is a work about it exist ?