Geometry with hyperreals/surreals coefficients

[quickfur]

[This is a branch off the discussion about ∞-polytopes, but I thought I should start a new topic in order not to distract from the focus on ∞-polytopes.]

The use of hyperreals/surreals for geometric computations came up in the thread about infinite-dimensional polytopes, but since geometry involving infinite/infinitesimal quantities (as an inherent part of the coefficient field) is AFAIK barely explored and thus poorly understood, I thought it might be fruitful to first consider what geometry might look like in finite-dimensional space, but one in which the usual coefficient field of real numbers is augmented with non-finite quantities like the hyperreals or surreals. For example, what could we say about the properties of geometry in *R³ or No³?

One thing for sure: the usual geometry still works as before in the finite subspace of this augmented space -- you'd have the old set of finite regular polytopes, etc.. But now there may be new objects that are introduced. For example, one could now construct a sphere that contains a linear apeirotope, for example. It would be a sphere of non-finite radius. One may also construct polyhedra with "points at infinity", i.e., one or more points that contain non-finite coordinates. One may also construct infinitesimal polytopes, or polytopes that contain infinitesimal elements. One may conceivably also embed the Long Line in this space (though that has yet to be confirmed).

One thing that could potentially fundamentally alter geometry in such a space is the possibility of defining certain infinite series to converge to real numbers displaced by an infinitesimal. OT1H this could be used to distinguish between things that in normal geometry are indistinguishible, but OTOH it may also prove problematic when certain computations yield results that don't match up because they differ by an infinitesimal.

What else can be said about such a space? Any ideas? How would one go about computing, say, the angle between a line in finite subspace and a line containing one or more non-finite coefficients? What about vector operations like dot products and linear transformations? What can be said about linear transformations involving non-finite or infinitesimal coefficients?

[mr_e_man]

There's some discussion of this in Keisler's book, section 10.8 . https://people.math.wisc.edu/~keisler/chapter_10.pdf

[quickfur]

There's some discussion of this in Keisler's book, section 10.8 . https://people.math.wisc.edu/~keisler/chapter_10.pdf

Cool chapter! Interesting discussion of vectors with real/non-real directions/lengths. But not much in the way of polyhedral geometry, though.

Though based on the real/non-real distinction, it would appear that in a space endowed with infinite/infinitesimal coefficients there is a distinction between the polygon of infinite degree and the apeirotope. The former has a digonal angle infinitesimally close to, but not exactly equal to, 180°, has vertices with infinite coordinates, and spans a closed circle of infinite radius; the latter has exactly 180° digonal angles, can have vertices with only real coordinates, and does not span a closed circle (though it can be enclosed by a circle of infinite radius).

Among many other things, of course. But this is the first thing that came to mind.

[adam ∞]

Though based on the real/non-real distinction, it would appear that in a space endowed with infinite/infinitesimal coefficients there is a distinction between the polygon of infinite degree and the apeirotope. The former has a digonal angle infinitesimally close to, but not exactly equal to, 180°, has vertices with infinite coordinates, and spans a closed circle of infinite radius; the latter has exactly 180° digonal angles, can have vertices with only real coordinates, and does not span a closed circle (though it can be enclosed by a circle of infinite radius).

In terms of surreal numbers, an apeirogon = an ω-gon ("omegagon"), {ω} with ω edges, edges meet at exactly 180 degrees - this is the same as a segmented infinite line segment, the 1-d tiling of line segments is the same object, and this is modular, where the far right meets with the far left side like a circle, like all other regular polygons. An embedded {ω} is round and curved a perfect circle, just as an embedded flat torus is round like a donut.

{ω-1} has ω-1 edges, an odd number of edges, meeting just short of 180 degrees, forming what looks like an irregular circle with diameter (ω-1)/π

Can you explain what you mean by how the first you mentioned "spans a closed circle of infinite radius" and the second "does not span a closed circle (though it can be enclosed by a circle of infinite radius)" ?


I think the distinction of an alternative type of geometry here may have gone over my head- how is this different from standard geometry taking place in a typical infinite space?

[quickfur]

An apeirogon with edges that meet at 180° has no beginning and no end, it's parallel to a straight line so the ends never meet. In a space endowed with surreal coordinates, however, one can construct a circle that contains the entirety of this apeirogon/straight line by setting its radius to an infinite number like w. (Or, for that matter, w/2, or √w, or √√w, or the inverse Ackermann function of w -- all of them are provably larger than any finite number so a circle of that radius will be larger than the extent of the straight line.)

The limiting shape of a regular n-gon as n→∞, however, is an entirely different object (in a space endowed with surreal coefficients, that is). It's a closed polygon with an infinite number of edges, and the edges meet at an angle of (180-s)° where s is an infinitesimal. (They do not meet at exactly 180°.)

Of course, one can also construct "long" lines: lines of the form x = k*v where v is any vector and k is allowed to be any surreal number, not just a real number. Such lines cannot be contained by any circle, even those with infinite radii. Parallel to these long lines one can construct "long apeirogons" that cannot be contained by any circle of infinite radius. These long apeirogons are structurally different from normal apeirogons, however: they contain an infinite number of "gaps" separating disconnected unbounded segments of the long apeirogon. For example, between w and edges a finite number of hops away from the origin there's an infinite gap. In fact, an infinite number of gaps: between every multiple and power of w there's an infinite gap (e.g., between w, w/2, w/3, w/4, etc., as well as between w, √w, √√w, log w, etc..). I'm not 100% sure but I surmise these gaps are "dense": between every two gaps there's another gap.

[adam ∞]

We can number the edges of all polygons in the standard way such that the last edge is next to the first edge. Same for {∞} the apeirogon. Edge #∞ is right next to edge #1, which means that the far right leads to the far left. You can see this same modular property in how the increasing size of a circle decreases its curvature with a limit at a perfectly flat straight infinite line.. You can see this same property in projective and inversive geometry, and in the concept of a generalized circle. An infinite circle is an infinite line, an infinite polygon is an infinite line, and they all have the modular property that the far right side leads to the far left. This is the modularity of space itself. Infinite space necessarily has this modular property. True for the apeirogon, which is the 1-dimensional case of the hypercubic honeycomb, true for all hypercubic honeycombs, true for an infinitely long line, true for a flat torus, true for an infinite plane (same thing), true for a (flat) infinite circle, true for the number line, true for infinite space of any dimension, true of time and everything else equivalent.

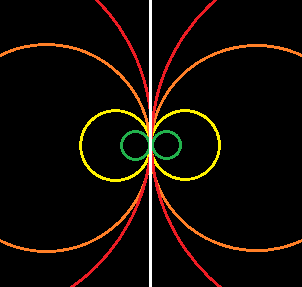
[adam ∞]

The blue meets up with the red in two places for all four circles depicted, including the infinite flat one.

[quickfur]

[...] An infinite circle is an infinite line, an infinite polygon is an infinite line, and they all have the modular property that the far right side leads to the far left. This is the modularity of space itself. Infinite space necessarily has this modular property.

To me, this is not self-evident at all. Why must space necessarily be modular? That's just an artificial construct we impose upon a space that's flat and unbounded in all directions. Of course, the study of modular spaces itself can be very interesting, but Euclidean space itself has no such property. None of the Euclidean axioms imply such a thing.

[adam ∞]

Euclidean space itself has no such property. None of the Euclidean axioms imply such a thing.

Space ain't Euclidean.

This isn't a preconceived construction being imposed on something, we are looking at how shapes behave in space, and this is informing us about the properties of space.

Whether it is self evident or not, the apeirogon and the infinite circle proves that infinite space is modular. Infinite lines are circles.

[adam ∞]

How can an apeirogon be a completed object, have side #infinity next to side #1 and not have the far right leading to the far left? An apeirogon is both a circle and an infinite line at the same time. They're the exact same thing.

[quickfur]

Like I said, we're starting out with incompatible definitions of infinity, so we're unlikely to ever come to any agreement.

If you're not working in Euclidean space, then you'd better define exactly what space you're working in, otherwise we're just talking past each other.

[adam ∞]

Like I said, we're starting out with incompatible definitions of infinity, so we're unlikely to ever come to any agreement.
If you're not working in Euclidean space, then you'd better define exactly what space you're working in, otherwise we're just talking past each other.

What you are proposing here based on hyperreals, surreals and / or a point at infinity, is not Euclidean. Also, hyperreals, surreals and a point at infinity are not representative of the way you have previously described about your conception of infinity from what I can understand.

For example, ω and ω-1 are distinct. The extended reals behave differently than hyperreals and surreals, and it depends on whether you base it on the affinely extended or projectively extended line.

Generally speaking, if you start with Euclid's axioms and try to construct an apeirogon or an actually infinite circle, and see how it actually behaves, you find that not all of Euclid's axioms can be true, even within supposedly Euclidean geometry. Our physical space is also not Euclidean.

If you are going to use hyperreals, surreals, a number like omega represents an actual infinity, not a potential infinity.

If you use actual infinity, Euclid's second axiom is either false, or needs to be reinterpreted, depending on how it is worded:

" Any terminated straight line may be extended indefinitely. "
" Any line segment can be made as long as you like (that is, extended indefinitely). "

The parallel postulate also works differently with actual infinity, and depends on what type of infinite angles are allowed, and what size of infinity is used. Depending on how it is stated, it is either false, or needs to be reinterpreted. For example, if you have a space that is ω units wide, a line that is ω units long will behave differently than if you allow lines that are 2ω - Like having lines on a sphere that are longer than the sphere's circumference. If you don't allow lines longer than ω in a space that is ω units wide, the parallel postulate is false. If you do allow lines longer than ω, the parallel postulate works differently.

For the real projective line with a point at infinity, the far left meets up with the far right:



The affinely extended real number line has two points at infinity, +∞ and -∞, with infinities that are actual, but not "definite"- meaning that they are not potential, "endless" infinities, there really is a point there, but "∞" here is not a distinct number like it is for hyperreals and surreals. For this type of geometry, ∞+1 is treated as equaling ∞.

The affinely extended real number line and corresponding terminology without modification leads to contradiction, and for example, doesn't allow for an object more than half the length of the space itself, since the entire space is presented as if its 2∞ units wide, but they treat 2∞ as being equal to ∞. This system doesn't allow you to distinguish between ∞ and ∞/2 either. Really, the affinely extended line is just a subsection of the real projective line, with points at "∞/2" labeled as "∞", resulting in a space that is only hemi-infinite. (Just the bottom half of the above image)

[adam ∞]

In an actually infinite space, with a circle increasing in size, reaching an infinite straight line, how can the far right not lead to the far left? Do you think of it as snapping apart at some point or something? Before, you have mentioned some kind of "gap", do you mean like a literal hole where part of the object is not connected? Like, as in, an apeirogon is not a connected object?

If an apeirogon starts out as a connected 3-gon, then a 4-gon, etc, do you think of it as like, as long as the angle between the edges is less than 180 it is connected, but that at infinity, it is no longer connected somehow? If so, how can you justify such a conclusion? If it is a connected whole the entire time and we are just adding to it, why would it snap apart at some point, and how is that a meaningful geometric object if it is broken? If you start with a polygon with angles meeting just short of 180 degrees, take any local subsection of it, add one more line, and adjust it accordingly, where is the "gap"?

Do you see that, if you a proposing exploring some geometry with actual infinite lengths, that the infinite lines you are dealing with are necessarily identical to the non-segmented apeirogon? Which is the same as a flat, infinite circle?

[adam ∞]

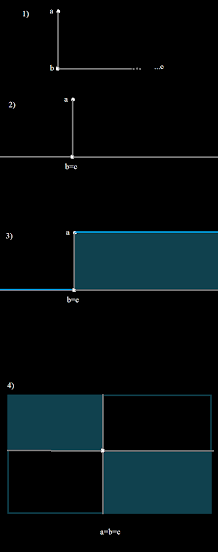
Consider the following illustration, constructing something like a triangle which has infinite length.

1) Start with points a and b, the length of the line segment ab is a finite length at first.

Now, let us consider joining point b with point c, and there is a distance of ω between b and c.

2) a distance of ω returns to b, so b=c

3) connecting a to c

4) now, extend a, so that it reaches a distance of ω from b=c. Now a=b=c.

[quickfur]

Like I said, we're starting out with incompatible definitions of infinity, so we're unlikely to ever come to any agreement.
If you're not working in Euclidean space, then you'd better define exactly what space you're working in, otherwise we're just talking past each other.

What you are proposing here based on hyperreals, surreals and / or a point at infinity, is not Euclidean.

It's not Euclidean, but it's an extension of Euclidean geometry.

hyperreals, surreals and a point at infinity are not representative of the way you have previously described about your conception of infinity from what I can understand. [...]

You appear to think there's necessarily a single entity called "infinity". But it's clear that there are numerous infinities, and not all are comparable with each other. The infinity introduced in projective geometry, for example, has nothing to do with the infinities in the surreals, for example. And the infinite surreals are distinct from the Cantorian ordinal and cardinal infinities, even though they are defined based on them. Their arithmetic works completely differently, for one thing. There's also Wheel Theory where division is always defined, including division by 0, which yields an element that's arbitrarily close to every number (but the laws of arithmetic are somewhat modified, because it's not a field anymore). So a completely different kind of infinity candidate.

Each choice of arithmetic or geometric system involving infinite quantities will lead to drastically different conclusions.

[adam ∞]

You appear to think there's necessarily a single entity called "infinity". But it's clear that there are numerous infinities, and not all are comparable with each other.

That is interesting that to you it appears that I think there is a single entity called "infinity". I have spent a lot of the time in these discussions going into a lot of detail about a lot of different types of infinity, and what you just responded to was about distinctions I was making between various types of infinity.

The version of infinity you have been talking about in other posts seems to be different from what you are proposing here, is that correct?

[quickfur]

Now I'm starting to understand why mathematicians hate the word "infinity". It has been overloaded to refer to multiple, mutually incompatible things, and when the word is used in a discussion it's completely ambiguous just what exactly is being referred to. Yet people throw it around as if it's referring to a single, well-defined thing. Or worse yet, the use of a single word to refer to all those diverse meanings misleads people into conflating incompatible things into one, as if they were the same thing, when actually each meaning contradicts the other and cannot possibly coexist in the same system, much less as a single entity.

I don't have a single conception of "infinity", as though it were a single, coherent thing. Depending on the system being used in a particular discussion, there may be a specific entity (or a group of entities) that have properties that could be construed to be "infinity". But that in no way implies that the "infinities" belonging to multiple systems have anything to do with each other. We may sometimes even compare such things across different systems as a way of investigating their commonalities or differences, but that does not mean we can just conflate them together.

The kind of "infinities" or system of arithmetic involving non-finite numbers that I'm looking for in this particular investigation is the kind that would lead to a consistent geometry with nice properties that could describe objects of provably non-finite dimension. I'm not sure how such a system would look like yet, or whether there could be multiple such systems that may be incompatible with each other. It's already starting to become clear to me that an infinite-dimensional geometry with real number coefficients necessarily has "holes" or incongruences that lack some of the nice closure properties of finite-dimensional space; that's why I'm looking into extensions of the coefficient field to things like hyperreals or surreals in order to obtain a closed system with nicer properties.

Whether such a system in the end will turn out to have any relation to what most people think of as "infinite-dimensional space", is anybody's guess.