Generating Vertex-Facet incidence matrix...?
26 posts
• Page 1 of 1
If you choose to define the polytope as a convex hull of a set of points, you can eliminate all of the points which can be represented as convex combination of other points. Once you eliminate all such points, you are left with the vertexes. From there, you can take any d of them (if they're in d dimensions) and determine whether or not all of the vertexes are on the same side of the hyperplane determined by those d vertexes. If they are, then the convex hull of all of the vertexes in that hyperplane is a facet of the polytope.
Let's do an example. Let's take the following set of 4-d points:
(0, 0, 0, 0)
(0, 3, 9, 27)
(1, 2, 3, 4)
(2, 4, 8, 16)
(3, 9, 27, 81)
(4, 16, 64, 256)
(5, 25, 125, 625)
(6, 36, 216, 1296)
First off, we can eliminate (0, 3, 9, 27) because it is a convex combination of ( 0, 0, 0, 0 ) and ( 3, 9, 27, 81 ). Now, if we take four of them:
(0, 0, 0, 0)
(1, 2, 3, 4)
(2, 4, 8, 16)
(3, 9, 27, 81)
we can determine the hyperplane which contains those four. With some linear algebra, we can determine that these four vertexes lie in the hyperplane made of all points x such that x dot ( 6, 1, -4, 1 ) equals zero. Now, if we take the dot product of an arbitrary vertex with ( 6, 1, -4, 1 ), we're going to get a number that's greater-to, equal, or less-than zero (or whatever our in-hyperplane dot-product is). Let's do this with all of the vertexes.
(0, 0, 0, 0) . ( 6, 1, -4, 1 ) = 0
(1, 2, 3, 4) . ( 6, 1, -4, 1 ) = 0
(2, 4, 8, 16) . ( 6, 1, -4, 1 ) = 0
(3, 9, 27, 81) . ( 6, 1, -4, 1 ) = 0
(4, 16, 64, 256) . ( 6, 1, -4, 1 ) = 40
(5, 25, 125, 625) . ( 6, 1, -4, 1 ) = 180
(6, 36, 216, 1296) . ( 6, 1, -4, 1 ) = 504
Now, because all of them were greater or equal (or if they had all been less-than or equal to) to our in-hyperplane dot-product, this hyperplane determines a facet and all of the vertexes in that hyperplane are part of the facet.
So, if we go through all of the 7 choose 4 choices of four vertexes out of our seven, we can find all of our facets. So, we can find all of the vertexes and all of the facets and the vertex-facet incident matrix without knowing anything about the edges, ridges, or other intermediate levels of the face-lattice. If I read my tea-leaves correctly, I believe this is a 4-dimensional polytope with seven vertexes and thirty-five tetrahedronal facets.
As for your question about what sorts of restrictions there are on face-lattices of polytopes... There are a bunch of them. But, it's going to take some terminology here. This comes fairly directly from the book Lectures On Polytopes by Gunter M. Ziegler. I highly recommend this book. But, it does require a fair comfort with some linear algebra.
The face-lattice can be viewed as a poset (partially-ordered set). A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b.
Every two elements a and b have a unique, minimal upper-bound called the join of a and b (the smallest-dimensional face which both of these faces belong to). Every two elements a and b have a unique, maximal lower-bound called the meet of a and b (the largest-dimensional face which both of these faces share).
The minimal elements of a lattice (other than the "empty" face) are called the atoms. For face-lattices, the atoms are the vertexes of the polytope. The maximal elements of a lattice (other than the whole polytope) are called the co-atoms.
A lattice is called atomic if every node in the lattice (other than the "empty" face) is the join of two atoms. For a face-lattice, this means that for any face f (other than the "empty" face), there are two (possibly identical) vertexes a and b such that f is the smallest-dimensional face that contains both of those vertexes.
A lattice is called co-atomic if every node in the lattice (other than the whole polytope) is the meet of two co-atoms.
And, we define the rank of a node in the face-lattice as one more than the dimension of the face that node represents. r(F) = dim(F) + 1. The rank of the empty face is zero.
An interval (a,b) (usually with square-brackets, but this UBB is annoying about those) is the subgraph of the lattice rooted at a and ending at b.
So, enough with definitions.... on to the properties.
It's all polytopes: Every interval (a,b) of the lattice is also the face lattice of a convex polytope of dimensions r(b) - r(a) - 1.
Diamond property: Every interval of length two has exactly four elements. If r(b) - r(a) = 2, then there are exactly two nodes c and d such that a is less than both c and d, both c and d are less than b, and neither c nor d is less than the other.
Opposites are dual: If you turn the face lattice upside-down, it is still the face lattice of a polytope -- the dual polytope.
Atomicness: Face-lattices of polytopes are both atomic and co-atomic.
Let's do an example. Let's take the following set of 4-d points:
(0, 0, 0, 0)
(0, 3, 9, 27)
(1, 2, 3, 4)
(2, 4, 8, 16)
(3, 9, 27, 81)
(4, 16, 64, 256)
(5, 25, 125, 625)
(6, 36, 216, 1296)
First off, we can eliminate (0, 3, 9, 27) because it is a convex combination of ( 0, 0, 0, 0 ) and ( 3, 9, 27, 81 ). Now, if we take four of them:
(0, 0, 0, 0)
(1, 2, 3, 4)
(2, 4, 8, 16)
(3, 9, 27, 81)
we can determine the hyperplane which contains those four. With some linear algebra, we can determine that these four vertexes lie in the hyperplane made of all points x such that x dot ( 6, 1, -4, 1 ) equals zero. Now, if we take the dot product of an arbitrary vertex with ( 6, 1, -4, 1 ), we're going to get a number that's greater-to, equal, or less-than zero (or whatever our in-hyperplane dot-product is). Let's do this with all of the vertexes.
(0, 0, 0, 0) . ( 6, 1, -4, 1 ) = 0
(1, 2, 3, 4) . ( 6, 1, -4, 1 ) = 0
(2, 4, 8, 16) . ( 6, 1, -4, 1 ) = 0
(3, 9, 27, 81) . ( 6, 1, -4, 1 ) = 0
(4, 16, 64, 256) . ( 6, 1, -4, 1 ) = 40
(5, 25, 125, 625) . ( 6, 1, -4, 1 ) = 180
(6, 36, 216, 1296) . ( 6, 1, -4, 1 ) = 504
Now, because all of them were greater or equal (or if they had all been less-than or equal to) to our in-hyperplane dot-product, this hyperplane determines a facet and all of the vertexes in that hyperplane are part of the facet.
So, if we go through all of the 7 choose 4 choices of four vertexes out of our seven, we can find all of our facets. So, we can find all of the vertexes and all of the facets and the vertex-facet incident matrix without knowing anything about the edges, ridges, or other intermediate levels of the face-lattice. If I read my tea-leaves correctly, I believe this is a 4-dimensional polytope with seven vertexes and thirty-five tetrahedronal facets.
As for your question about what sorts of restrictions there are on face-lattices of polytopes... There are a bunch of them. But, it's going to take some terminology here. This comes fairly directly from the book Lectures On Polytopes by Gunter M. Ziegler. I highly recommend this book. But, it does require a fair comfort with some linear algebra.
The face-lattice can be viewed as a poset (partially-ordered set). A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b.
Every two elements a and b have a unique, minimal upper-bound called the join of a and b (the smallest-dimensional face which both of these faces belong to). Every two elements a and b have a unique, maximal lower-bound called the meet of a and b (the largest-dimensional face which both of these faces share).
The minimal elements of a lattice (other than the "empty" face) are called the atoms. For face-lattices, the atoms are the vertexes of the polytope. The maximal elements of a lattice (other than the whole polytope) are called the co-atoms.
A lattice is called atomic if every node in the lattice (other than the "empty" face) is the join of two atoms. For a face-lattice, this means that for any face f (other than the "empty" face), there are two (possibly identical) vertexes a and b such that f is the smallest-dimensional face that contains both of those vertexes.
A lattice is called co-atomic if every node in the lattice (other than the whole polytope) is the meet of two co-atoms.
And, we define the rank of a node in the face-lattice as one more than the dimension of the face that node represents. r(F) = dim(F) + 1. The rank of the empty face is zero.
An interval (a,b) (usually with square-brackets, but this UBB is annoying about those) is the subgraph of the lattice rooted at a and ending at b.
So, enough with definitions.... on to the properties.
It's all polytopes: Every interval (a,b) of the lattice is also the face lattice of a convex polytope of dimensions r(b) - r(a) - 1.
Diamond property: Every interval of length two has exactly four elements. If r(b) - r(a) = 2, then there are exactly two nodes c and d such that a is less than both c and d, both c and d are less than b, and neither c nor d is less than the other.
Opposites are dual: If you turn the face lattice upside-down, it is still the face lattice of a polytope -- the dual polytope.
Atomicness: Face-lattices of polytopes are both atomic and co-atomic.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Particularly, the following fail to be face-lattices of any convex polytope because the highlighted nodes: fail to be the join of two vertexes (not atomic), fail to be the meet of two facets (not co-atomic), are a sublattice of length 2 with more than four nodes (violates the diamond property).


- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Hello Pat,
Thanks for your response.
I do have the book <u>Lectures on Polytopes</u>, by Gunter M. Ziegler... the author that prefers the term 'polar' to 'dual'... Sometimes I find it difficult to understand what he's talking about...
"The face-lattice can be viewed as a poset (partially-ordered set). A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b.
Every two elements a and b have a unique, minimal upper-bound called the join of a and b (the smallest-dimensional face which both of these faces belong to). Every two elements a and b have a unique, maximal lower-bound called the meet of a and b (the largest-dimensional face which both of these faces share). "
That's interesting... that's precisely a confusion I have. I don't quite understand what you mean by "A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b." In particular, what is "an always increasing path from a to b."
Also... I know Cinderella has commands for 'join' and 'meet'. Can these concepts be described in a more general realm?
I don't know much about graphs yet...
"convex combination"...? What precisely is a 'convex' combination? I don't understand...?
"in-hyperplane dot-product"... Is this something that has a general definition? It wouldn't be one of the various products that one might use in Clifford, Geometric, or Multi-linear algebra? It kinda sounds like it might be...
If not, I suppose it might not be too difficult to come up with a 'product' which provided this information.
Definitions... okay, need something more basic. What precisely is the definition of a 'lattice'...? Unfortunately, the way Gunter defines things usually leaves my head buzzing...!
I also have the book <u>Convex Polytopes</u>, by Branko Grunbaum. Unfortunately, this book too is also at a pretty advanced level.
I also have Coxeter's <u>Regular Polytopes</u>. However, I've always had some trouble with reading Coxeter. He doesn't write at such an advanced level, but I don't know... somehow I just have trouble following him
I also have some books on Clifford, Geometric, and Multi-linear algebra... A couple that I think are pretty good are <u>Clifford Algebras and Spinors</u>, by Pertti Lounesto and David Hestenes books <u>New Foundations for Classical Mechanics</u> and <u>Clifford Algebra to Geometric Calculus</u> (with Garret Sobczyk).
I don't have an advanced understanding of Geometric algebra, but if some of this can be described in terms of multi-vectors and products of Geometric algebra, I do have some significant familiarity with these... at least, basics of Geometric algebra.
I'll have to study your post more intensively to ask more specific questions.
I also just noticed... it appears you just added two images to your post. I was about to ask... I guess you use the html tag img within the square brackets, like when posting a URL to the board? Can the images be GIFs, JPEGs, or PNGs? What image formats can be posted? Are there any restrictions?
That's interesting... I put the regular html tags with the greater than and less than signs for the underlines here. Can you use the regular html tags for URLs and other html markup?
Thanks for your response.
I do have the book <u>Lectures on Polytopes</u>, by Gunter M. Ziegler... the author that prefers the term 'polar' to 'dual'... Sometimes I find it difficult to understand what he's talking about...
"The face-lattice can be viewed as a poset (partially-ordered set). A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b.
Every two elements a and b have a unique, minimal upper-bound called the join of a and b (the smallest-dimensional face which both of these faces belong to). Every two elements a and b have a unique, maximal lower-bound called the meet of a and b (the largest-dimensional face which both of these faces share). "
That's interesting... that's precisely a confusion I have. I don't quite understand what you mean by "A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b." In particular, what is "an always increasing path from a to b."
Also... I know Cinderella has commands for 'join' and 'meet'. Can these concepts be described in a more general realm?
I don't know much about graphs yet...
"convex combination"...? What precisely is a 'convex' combination? I don't understand...?
"in-hyperplane dot-product"... Is this something that has a general definition? It wouldn't be one of the various products that one might use in Clifford, Geometric, or Multi-linear algebra? It kinda sounds like it might be...
If not, I suppose it might not be too difficult to come up with a 'product' which provided this information.
Definitions... okay, need something more basic. What precisely is the definition of a 'lattice'...? Unfortunately, the way Gunter defines things usually leaves my head buzzing...!
I also have the book <u>Convex Polytopes</u>, by Branko Grunbaum. Unfortunately, this book too is also at a pretty advanced level.
I also have Coxeter's <u>Regular Polytopes</u>. However, I've always had some trouble with reading Coxeter. He doesn't write at such an advanced level, but I don't know... somehow I just have trouble following him
I also have some books on Clifford, Geometric, and Multi-linear algebra... A couple that I think are pretty good are <u>Clifford Algebras and Spinors</u>, by Pertti Lounesto and David Hestenes books <u>New Foundations for Classical Mechanics</u> and <u>Clifford Algebra to Geometric Calculus</u> (with Garret Sobczyk).
I don't have an advanced understanding of Geometric algebra, but if some of this can be described in terms of multi-vectors and products of Geometric algebra, I do have some significant familiarity with these... at least, basics of Geometric algebra.
I'll have to study your post more intensively to ask more specific questions.
I also just noticed... it appears you just added two images to your post. I was about to ask... I guess you use the html tag img within the square brackets, like when posting a URL to the board? Can the images be GIFs, JPEGs, or PNGs? What image formats can be posted? Are there any restrictions?
That's interesting... I put the regular html tags with the greater than and less than signs for the underlines here. Can you use the regular html tags for URLs and other html markup?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Paul wrote:"The face-lattice can be viewed as a poset (partially-ordered set). A node in the face-lattice a is less-than a node b if there is an always increasing path from a to b.
Every two elements a and b have a unique, minimal upper-bound called the join of a and b (the smallest-dimensional face which both of these faces belong to). Every two elements a and b have a unique, maximal lower-bound called the meet of a and b (the largest-dimensional face which both of these faces share). "
I am using the word "node" to mean a vertex in the face-lattice. This is to try to keep from confusing the vertexes of the polytope with the vertexes of the face-lattice. You've drawn some face lattices. They're usually drawn with the whole polytope at the top and the empty face at the bottom. Here's one with labels for convenience.
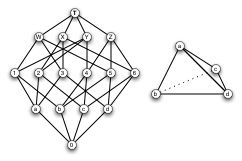
A graph like this is a lattice if it has a single node at the top and single node at the bottom. Also, you have to be able to orient it in tiers like there where no elements within a tier link directly to each other. All face-lattices are lattices. An always increasing path is one where you never have to go downward in the graph. For example, the path from a to 3 to X is an always increasing path. Thus, we can say that a is less than X. However, a is not less than Z. Because, to walk from a to Z, you'd have to work downward at some point. a to 2 to c to 4 to Z or some such path. At the same time, Z isn't less than a either. That's what makes this a partially-ordered set instead of a totally ordered set.
Now, the atoms are a, b, c, d and the co-atoms are W, X, Y, Z. The node 2 is the join of a and c. It is the lowest node on the graph with a less than it *and* c less than it. W here is the join of a, b, and d.
"convex combination"...? What precisely is a 'convex' combination? I don't understand...?
Make a matrix V where each row is the coordinates of a vertex of the polytope. Now, if you can find a vector c whose coordinates are all non-negative and whose coordinates sum up to one such that c<sup>T</sup>V = x<sup>T</sup>, then x is a convex combination of the vertexes.
"in-hyperplane dot-product"... Is this something that has a general definition? It wouldn't be one of the various products that one might use in Clifford, Geometric, or Multi-linear algebra? It kinda sounds like it might be...
A hyperplane can be defined by two parameters: a normal vector n and a real number d. A hyperplane is all points x such the n . x = d. By the "in-hyperplane dot-product", I simply mean the dot-product of the vertex by the normal n which defines the hyperplane.
I don't have an advanced understanding of Geometric algebra, but if some of this can be described in terms of multi-vectors and products of Geometric algebra, I do have some significant familiarity with these... at least, basics of Geometric algebra.
Well, the dot-product that I'm using above is very much a pre-requisite for geometric algebra. I'm hoping that I just confused you by calling it an "in-hyperplane" one.
I also just noticed... it appears you just added two images to your post. I was about to ask... I guess you use the html tag img within the square brackets, like when posting a URL to the board? Can the images be GIFs, JPEGs, or PNGs? What image formats can be posted? Are there any restrictions?
I think they can be any image format supported by people's web browsers. And, as a technical note, the square-brackets things are BBCode, not HTML. This board doesn't support the HTML image tag.
That's interesting... I put the regular html tags with the greater than and less than signs for the underlines here. Can you use the regular html tags for URLs and other html markup?
This forum only accepts a very limited subset of HTML. It won't let you do paragraphs, images, hyperlinks... I don't think it lets you do tables or bold or italic or pre-formatted blocks or centering or lists... Some of that stuff, you can get done sorta with BBCodes. But, much of it, you just have to do without. The only html tags that I know for sure that it likes are 'sup' and 'sub'.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Hello Pat,
Thanks for your response.
Concerning the inner product... It's just that I recall that there a whole bunch of 'inner product's. Although it looks like allot ot the variation surrounds treatment of scalars.
I gather you're probably referring to something like the Lounesto (left) contractive inner product, or the Hestenes semi-symmetric inner product...
Products of multivectors
Is this correct?
Thanks for your response.
Concerning the inner product... It's just that I recall that there a whole bunch of 'inner product's. Although it looks like allot ot the variation surrounds treatment of scalars.
I gather you're probably referring to something like the Lounesto (left) contractive inner product, or the Hestenes semi-symmetric inner product...
Products of multivectors
Is this correct?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Paul wrote:I gather you're probably referring to something like the Lounesto (left) contractive inner product, or the Hestenes semi-symmetric inner product...
I think you're bringing in much bigger guns than needed. If you consider two column vectors a and b as matrixes, then the dot-product is given by a<sup>T</sup>b. If you want to get out the big guns, then we've assumed that the vector coordinates are in an orthonormal basis. That is, the dot-product is such that the basis vectors are such that the inner-product of any basis vector with itself is the scalar one. And, the dot-product of any basis vector with a different basis vector is zero.
So, for all of this, we're assuming the standard basis vectors for R<sup>n</sup> = { ( 1, 0, 0, 0, ... ), ( 0, 1, 0, 0, ... ), ( 0, 0, 1, 0, ... ), ... }.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Paul wrote:what software did you use to generate the graphs in your last two posts?
I used OmniGraffle Professional.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Hello Pat,
Thanks for your response.
Nice software... too bad it's for the Mac.
I think I understand most of it... now.
I'm still a bit confused about 'convex' combination. Is there a geometric interpretation for this?
Would a 'linear' combination also be a 'convex' combination?
Also...
"If I read my tea-leaves correctly, I believe this is a 4-dimensional polytope with seven vertexes and thirty-five tetrahedronal facets."
If I'm following correctly, the information the dot product yielded tells us that those 4 points are in one hyperplane... in this case, one realm, one 3D space. It's one cell of the polytope.
However, although it's unlikely, is it possible, for instance, that all 4 points are coplanar?
Also... can we really be sure that all the other cells are going to be the same as this one? Even if each is composed of 4 points, couldn't some of them just be a 2D face,... or something?
This kind of thinking is pretty new to me... but, how much of this can we be sure about? And do we need further information, and/or calculation to determine some of these things?
Thanks for your response.
Nice software... too bad it's for the Mac.
I think I understand most of it... now.
I'm still a bit confused about 'convex' combination. Is there a geometric interpretation for this?
Would a 'linear' combination also be a 'convex' combination?
Also...
"If I read my tea-leaves correctly, I believe this is a 4-dimensional polytope with seven vertexes and thirty-five tetrahedronal facets."
If I'm following correctly, the information the dot product yielded tells us that those 4 points are in one hyperplane... in this case, one realm, one 3D space. It's one cell of the polytope.
However, although it's unlikely, is it possible, for instance, that all 4 points are coplanar?
Also... can we really be sure that all the other cells are going to be the same as this one? Even if each is composed of 4 points, couldn't some of them just be a 2D face,... or something?
This kind of thinking is pretty new to me... but, how much of this can we be sure about? And do we need further information, and/or calculation to determine some of these things?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Paul wrote:Would a 'linear' combination also be a 'convex' combination?
Convex combinations are linear combinations with added restrictions on the coefficients. The coefficients must sum to one, and none of the coefficients can be negative. For example, the points (-1,-1) and (3,3) are linear combinations of the points (1,1) and (2,2), but they fail to be convex combinations (they fail to be in the convex hull of (1,1) and (2,2)) because not all of the coefficients are non-negative (in the (-1,-1) case) or the sum of the coefficients is greater than one (in the (3,3) case).
The geometric meaning is pretty much what we'd mean by "between" or in the "interior" of the set of points. If we had the set of points: { (1, 0, 0), (0, 1, 0), (0, 0, 1) }, then the convex combinations of those points (the convex hull of those points) would fill a triangle with those points as vertexes. If we added another point: ( 1/3, 1/3, 1/3 ), we'd still have the same convex combinations and convex hull.
"If I read my tea-leaves correctly, I believe this is a 4-dimensional polytope with seven vertexes and thirty-five tetrahedronal facets."
If I'm following correctly, the information the dot product yielded tells us that those 4 points are in one hyperplane... in this case, one realm, one 3D space. It's one cell of the polytope.
However, although it's unlikely, is it possible, for instance, that all 4 points are coplanar?
Also... can we really be sure that all the other cells are going to be the same as this one? Even if each is composed of 4 points, couldn't some of them just be a 2D face,... or something?
Those would be things that we'd have to check. However, the points that I chose were very particular ones. My points (except for the one that was a convex combination of two others) were the vertexes of the 4-dimensional cyclic polytope with seven vertexes. By virtue of special extra knowledge, I know that the point set is not degenerate... that no group of four points is coplanar.
I'm trying to think of whether that would affect the vertex-facet incidence matrix at all. Let's see. If I had the points: a=(0,0,0,0), b=(1,0,0,0), c=(0,1,0,0), d=(1,1,0,0), e=(0,0,0,1)... I would end up with four tetrahedronal facets and one square facet. But, I would have severe problems since my tetrahedronal facets overlap with each other. And, this problem wouldn't really just show up on its own.
I'm not really sure how best to algorithmically handle things like this then. One would want to check to see if all of the points fall into some less-than-full-dimensional space. The way Ziegler deals with this is that he works everything within the affine hull of the points or assumes that you've done a rotation and translation and dimensions reduction so that the affine hull and the embedding space are of the same dimension.
In my example with the five points: a, b, c, d, and e... the affine hull is the vector space spanned by a, b, c, and e (or equivalently, any three of the first four points plus 'e'). That affine hull is only three-dimensional and is the set of all points x such that x.(0,0,1,0) = 0. So, I would be looking for two-dimensional planes. They would be defined as all points x such that x.n = k for some real k *and* x.(0,0,1,0) = 0 and n doesn't equal (0,0,1,0). And, I way as well choose my n such that n.(0,0,1,0) = 0 or else I'm effectively only going to be taking advantage of using part of by n.
So, one would be well-advised to determine the rank of the matrix formed by the vertexes before entering into all of this.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
So, one would be well-advised to determine the rank of the matrix formed by the vertexes before entering into all of this.
I regret to admit I had forgotten exactly what the rank of a matrix is... so, please tell me if I'm following this correctly,... or, if at least I'm on the right track...
The rank of a matrix is determining the determinant of a minor of greatest order (dimension), including the whole matrix, that is non-zero. Is this accurate?
Now, I'm thinking this determinant of the minor kinda sounds like a wedge product... although I hadn't really thought of the wedge product in terms of matrices. If this is a wedge product, then doesn't it follow that the wedge product of the particular elements of the matrix in a particular minor will be zero if and only if the multi-vectors are parallel. Is this correct?
So, if all the vectors of the minors of any particular dimension k are all parallel (and parallelism is symmetric and transitive) to each other, then the wedge product of the vectors of the minor,... the determinant of the minor... will be zero. In fact, is it correct that the vectors will be in the same k-space because our vectors share a common origin...?
So, for instance, in the examples above, in 4D space, once we've determined a subset of the vertices that are in the same 3D realm through the "in-hyperplane" dot product, then I believe if all the 3x3 (3D) minors are zero, doesn't this mean that all the points are not only in the same 3D realm, but they're also in parallel 2D planes? ... and, in fact, since our vectors share a common origin, the same 2D planes?
So,... doesn't this mean that the rank of the matrix in the examples above will be less than 4 if all the vectors share a k-space less than 3...?
Is this what the rank is to tell us?
I'm also wondering if we might be able to determine all facets, of all k dimensions less than n, the dimension of the polytope itself, by taking the determinants of all the minors, and the whole matrix of vertices itself... somehow? Somehow I think this might get involved?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
I'm not really sure about the wedge-product thoughts. I'm fairly sure they won't be completely parallel though. But, they may not have full-dimension... I'm not 100% sure on my terminology here. But, in Clifford Algebra terms... if we've got four vectors that are in the same 2-D plane.... maybe: 0, e<sub>1</sub>, e<sub>4</sub>, and e<sub>1</sub> + e<sub>4</sub>... then we're going to get a zero coefficient for the e<sub>1234</sub> term in the Clifford product and somehow, the coeffiecients of the e<sub>123</sub>, e<sub>124</sub>, e<sub>134</sub>, and e<sub>234</sub> should also effectively indicate that these points are all in the same 2-D plane, but I'm not sure how this will show up yet. I'll have to ponder this some more and try some results.
But, yes... that's what the rank of a matrix is supposed to tell us... the size of the largest linearly-independent subspace represented by the matrix. And, the coefficient of the e<sub>123</sub> would represent the volume of the vectors in the product projected down to the e<sub>1</sub>, e<sub>2</sub>, e<sub>3</sub> space.
I'm sorry that I'm being so short and muddled here. I have to run at the moment. More later....
But, yes... that's what the rank of a matrix is supposed to tell us... the size of the largest linearly-independent subspace represented by the matrix. And, the coefficient of the e<sub>123</sub> would represent the volume of the vectors in the product projected down to the e<sub>1</sub>, e<sub>2</sub>, e<sub>3</sub> space.
I'm sorry that I'm being so short and muddled here. I have to run at the moment. More later....
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Bah.. actually, my memory of Clifford Algebras was at fault too... the Clifford product of any three vectors in the same plane is going to be zero, isn't it? It's not just that the multivector for that plane is going to be zero? I'm gonna have to brush up on my Clifford Algebras.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Ahh... okay.. during the day and night last night, I think I sorted some things out in my head. At the time that I read Lounesto's book, I hadn't seen the wedge product anywhere else. But, if I'm remembering right, then the wedge product could be quite useful.
With the Clifford product, e<sub>1</sub>e<sub>1</sub> = 1, but with the wedge product e<sub>1</sub>e<sub>1</sub> = 0, right? That could be quite useful.
Clifford algebras may still be the way to go though since they encompass both the dot-product and the wedge-product if used in special ways. For example... if you have two pure-vectors x and n, then x.n = ( xn + nx )/2 (where the product on the right is the Clifford product).
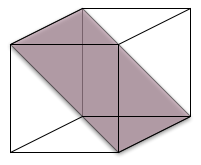
And, I can't see any way around needing the dot-product to determine whether a hyperplane bounds the polytope or slices through it. For example, using the wedge-product, one might be able to tell that the four vertexes on one face of a cube are coplanar, but would you be able to distinguish that face from one cut to include one edge and the diagonally opposed edge of the cube?
With the Clifford product, e<sub>1</sub>e<sub>1</sub> = 1, but with the wedge product e<sub>1</sub>e<sub>1</sub> = 0, right? That could be quite useful.
Clifford algebras may still be the way to go though since they encompass both the dot-product and the wedge-product if used in special ways. For example... if you have two pure-vectors x and n, then x.n = ( xn + nx )/2 (where the product on the right is the Clifford product).
And, I can't see any way around needing the dot-product to determine whether a hyperplane bounds the polytope or slices through it. For example, using the wedge-product, one might be able to tell that the four vertexes on one face of a cube are coplanar, but would you be able to distinguish that face from one cut to include one edge and the diagonally opposed edge of the cube?

- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
For example, using the wedge-product, one might be able to tell that the four vertexes on one face of a cube are coplanar, but would you be able to distinguish that face from one cut to include one edge and the diagonally opposed edge of the cube?
My first thought is to perhaps consider those convex combinations...?
There is another possible problem with all this, however. But, I'm not sure if this would be a problem here...
In 4D, for instance, bivectors get more complicated... as Lounesto calls it, some bivectors in 4D space are not 'simple'... 'simple' is like all bivectors in dimension < 4.
If I understand correctly, these nonsimple bivectors represent orthogonal planes in 4D space, and are written as the sum of two simple bivectors. However, even so, these two orthogonal planes are still mutually orthogonal to two other planes in 4D space... (I'm not really sure if this makes any difference, however...)
I'm just not sure if this is important. I'm just not sure...
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Paul wrote:My first thought is to perhaps consider those convex combinations...?
Well, yes... I suppose that it's possible, for any interior hyperplane, to find two vertexes not in the hyperplane such that the line segment between them intersects the hyperplane. I'm not sure at this point, how reasonable the math will turn out to be on this. Hopefully, I'll get to play with the math of all of this come the weekend.
A quick browsing of the google search "clifford algebra" "polytope" doesn't seem to show up much beyond some of Tony Smith's lattice stuff and maybe some stuff from David Rusin. Hmmm...
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
First off, I'm sorry that you're probably all getting asked for a password to "Members Resources" at http://www.csh.rit.edu. I've asked the admins there to fix that. Apparently, they've gone medieval and decided to censor all user pages until further notice. I apologize for the repeated inconvenience of this.
Let { v<sub>1</sub>, v<sub>2</sub>, v<sub>3</sub>, ..., v<sub>d</sub> } ⊆ vert(P) be some of the vertexes (represented as pure vectors) of a polytope P in R<sup>d</sup>.
Further, let n = ( v<sub>2</sub> - v<sub>1</sub> ) ∧ ( v<sub>3</sub> - v<sub>1</sub> ) ∧ ( v<sub>4</sub> - v<sub>1</sub> ) ∧ ... ∧ ( v<sub>d</sub> - v<sub>1</sub> ).
Claim: The vertexes v<sub>1</sub>, v<sub>2</sub>, v<sub>3</sub>, ..., v<sub>d</sub> determine a unique hyperplane in R<sup>d</sup> if and only if n ≠ 0.
Claim: If n ≠ 0, then n is the Hodge dual of a normal to that hyperplane.
Claim: A point p respresented as a pure vector lies in that unique hyperplane in R<sup>d</sup> if and only if ( p - v<sub>1</sub> ) ∧ n = 0.
Claim: Given points p<sub>1</sub> and p<sub>2</sub> such that ( p<sub>1</sub> - v<sub>1</sub> ) ∧ n ≠ 0 and ( p<sub>2</sub> - v<sub>1</sub> ) ∧ n ≠ 0 both have the same sign, then all of the points p such that p = ( p<sub>2</sub> - p<sub>1</sub> ) t + p<sub>1</sub> where 0 ≤ t ≤ 1 are such that ( p ∧ n ) have that same sign.
Claim: Given points p<sub>1</sub> and p<sub>2</sub> such that ( p<sub>1</sub> - v<sub>1</sub> ) ∧ n ≠ 0 and ( p<sub>2</sub> - v<sub>1</sub> ) ∧ n ≠ 0 have opposite signs, then there exists one and only one t such that ( ( p<sub>2</sub> - p<sub>1</sub> ) t + p<sub>1</sub> ) ∧ n = 0. Further, that t will satisfy 0 < t < 1.
Claim: If we run through all of the vertexes v ∈ vert(P), and with each, we note the sign of ( v - v<sub>1</sub> ) ∧ n, we will find that either they are all non-negative; they are all non-positive; or they are a mixture of positive, negative, and zero. If they are all non-negative or all non-positive, then the convex hull of those vertexes of sign zero is a facet of the polytope. If they are a mixture of positive, negative, and zero, then this hyperplane does not contain any facet of the polytope.
I believe that all of these claims are readily provable and follow fairly well in the order given. But, I haven't actually written out proofs, so I may have glossed something on my mental whiteboard.
Let { v<sub>1</sub>, v<sub>2</sub>, v<sub>3</sub>, ..., v<sub>d</sub> } ⊆ vert(P) be some of the vertexes (represented as pure vectors) of a polytope P in R<sup>d</sup>.
Further, let n = ( v<sub>2</sub> - v<sub>1</sub> ) ∧ ( v<sub>3</sub> - v<sub>1</sub> ) ∧ ( v<sub>4</sub> - v<sub>1</sub> ) ∧ ... ∧ ( v<sub>d</sub> - v<sub>1</sub> ).
Claim: The vertexes v<sub>1</sub>, v<sub>2</sub>, v<sub>3</sub>, ..., v<sub>d</sub> determine a unique hyperplane in R<sup>d</sup> if and only if n ≠ 0.
Claim: If n ≠ 0, then n is the Hodge dual of a normal to that hyperplane.
Claim: A point p respresented as a pure vector lies in that unique hyperplane in R<sup>d</sup> if and only if ( p - v<sub>1</sub> ) ∧ n = 0.
Claim: Given points p<sub>1</sub> and p<sub>2</sub> such that ( p<sub>1</sub> - v<sub>1</sub> ) ∧ n ≠ 0 and ( p<sub>2</sub> - v<sub>1</sub> ) ∧ n ≠ 0 both have the same sign, then all of the points p such that p = ( p<sub>2</sub> - p<sub>1</sub> ) t + p<sub>1</sub> where 0 ≤ t ≤ 1 are such that ( p ∧ n ) have that same sign.
Claim: Given points p<sub>1</sub> and p<sub>2</sub> such that ( p<sub>1</sub> - v<sub>1</sub> ) ∧ n ≠ 0 and ( p<sub>2</sub> - v<sub>1</sub> ) ∧ n ≠ 0 have opposite signs, then there exists one and only one t such that ( ( p<sub>2</sub> - p<sub>1</sub> ) t + p<sub>1</sub> ) ∧ n = 0. Further, that t will satisfy 0 < t < 1.
Claim: If we run through all of the vertexes v ∈ vert(P), and with each, we note the sign of ( v - v<sub>1</sub> ) ∧ n, we will find that either they are all non-negative; they are all non-positive; or they are a mixture of positive, negative, and zero. If they are all non-negative or all non-positive, then the convex hull of those vertexes of sign zero is a facet of the polytope. If they are a mixture of positive, negative, and zero, then this hyperplane does not contain any facet of the polytope.
I believe that all of these claims are readily provable and follow fairly well in the order given. But, I haven't actually written out proofs, so I may have glossed something on my mental whiteboard.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Paul (in email) wrote:Hence, I had thought that something like the Hodge dual would only work in 3D... perhaps 7D? However, I didn't think the Hodge dual would work in a general nD since there is no duality between vectors in bivectors in nD of the nature there is in 3D.
My understanding is that Hodge duality works in any number of dimensions d > 1. However, it is not generally duality between vectors and bivectors. In dimension d, it is a duality between 1-vectors (pure vectors) and (d-1)-vectors. (In fact, I believe it can be exploited even further to be a duality between k-vectors and (d-k)-vectors.)
I know that the dot-product (scalar-product, inner-product) works in any R<sup>d</sup>. And, Hodge-duality is defined in terms of the dot-product.
The goal of the Hodge dual (of a 1-vector) is to start with a 1-vector n (a pure vector in R<sup>d</sup>) and come up with a (d-1)-vector n<sup>*</sup> such that for any 1-vector v, v ∧ n = v.n. If the vector components are v<sub>k</sub> and n<sub>k</sub> respectively, then v.n = ∑ v<sub>k</sub>n<sub>k</sub>. You can check that if w<sub>k</sub> is used to denote the wedge product of the orthogonal unit vectors other than e<sub>k</sub>... that is to say: w<sub>k</sub> = e<sub>1</sub> ∧ e<sub>2</sub> ∧ ... ∧ e<sub>k-1</sub> ∧ e<sub>k+1</sub> ∧ ... ∧ e<sub>d</sub>, that n<sup>*</sup> = ∑ (-1)<sup>k+1</sup> n<sub>k</sub> w<sub>k</sub> will work to make v ∧ n = v.n for all v. It's a bit harder to verify that it's the only choice of n<sup>*</sup> which will work, but it is the only choice that works.
To my understanding, what doesn't work for dimensions other than 3 and 7 is a cross-product--a product of two vectors which results in a new vector perpendicular to the other two with the magnitude of the products of the magnitudes of the initial vectors when the initial vectors are perpendicular and a magnitude of zero when the two vectors are parallel. This is related to Hodge duality in dimension 3. I'm not sure exactly what it's related to in dimension 7 (but I believe has close ties with the octonions).
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
All that I've read so far is Lounesto's book Clifford Algebras and Spinors and Darling's Differential Forms and Connections. I have Porteous's Clifford Algebras and the Classical Groups but haven't read much of it yet. And, of course, I refer to mathworld and planetmath and wikipedia and Google incredibly often.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
I successfully used the wedge product to determine the facet hyperplanes in my simplex given only the vertexes in the Hidden Surface Removal applet that I wrote over the past few days.
I started with the list of vertexes:
Here is the relevant section of code:
I started with the list of vertexes:
- < 1, 0, 0, 0 >
< a, b, 0, 0 >
< a, c, d, 0 >
< a, c, e, f >
< a, c, e, -f >
- a = -(1/4)
b = √( 1 - a<sup>2</sup> )
c = ( a - a<sup>2</sup> ) / b
d = √( 1 - a<sup>2</sup> - c<sup>2</sup> )
e = ( a - a<sup>2</sup> - c<sup>2</sup> )/d
f = √( 1 - a<sup>2</sup> - c<sup>2</sup> - e<sup>2</sup> )
Here is the relevant section of code:
- Code: Select all
public Plane4D( Point4D aa, Point4D bb, Point4D cc, Point4D dd ) {
double ax = aa.getX();
double ay = aa.getY();
double az = aa.getZ();
double aw = aa.getW();
double e1 = ( bb.getX() - ax );
double e2 = ( bb.getY() - ay );
double e3 = ( bb.getZ() - az );
double e4 = ( bb.getW() - aw );
double cx = cc.getX() - ax;
double cy = cc.getY() - ay;
double cz = cc.getZ() - az;
double cw = cc.getW() - aw;
double e12 = e1 * cy - e2 * cx;
double e13 = e1 * cz - e3 * cx;
double e14 = e1 * cw - e4 * cx;
double e23 = e2 * cz - e3 * cy;
double e24 = e2 * cw - e4 * cy;
double e34 = e3 * cw - e4 * cz;
double dx = dd.getX() - ax;
double dy = dd.getY() - ay;
double dz = dd.getZ() - az;
double dw = dd.getW() - aw;
double e123 = e12 * dz - e13 * dy + e23 * dx;
double e124 = e12 * dw - e14 * dy + e24 * dx;
double e134 = e13 * dw - e14 * dz + e34 * dx;
double e234 = e23 * dw - e24 * dz + e34 * dy;
this.normal = new Point4D( e234, -e134, e124, -e123 );
this.offset = this.normal.dot( aa );
if ( this.offset < 0 ) {
this.normal = new Point4D( -e234, e134, -e124, e123 );
this.offset = this.normal.dot( aa );
}
};
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Hello Pat,
I wanted to ask... does it matter which direction the normal to the hyperplane is pointing?
That is, if the normal is a 1-vector, then it can be positive or negative... pointing away from the centroid of the polytope, or pointing towards the centroid...
Does the Hodge dual kinda automatically give you one or the other? Can you tell which is which from the cosine... the sign of the associated inner, dot product?
I wanted to ask... does it matter which direction the normal to the hyperplane is pointing?
That is, if the normal is a 1-vector, then it can be positive or negative... pointing away from the centroid of the polytope, or pointing towards the centroid...
Does the Hodge dual kinda automatically give you one or the other? Can you tell which is which from the cosine... the sign of the associated inner, dot product?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Hello again Pat,
That applet doesn't work in IE for me... it does work in Netscape, though... Do you need the Sun Java enabled?
Anyway... I'm not sure I understand. Is that a 3D cube and a 3D tetrahedron in the applet?
Also...
This part of your code looks like it might be taking the negative of some vector. Is it taking the negative of the normal if it turns out that we get the one pointing towards the centroid of the polytope?
Also... this hidden line stuff... Is the centroid of the polytope at the origin, at least of the main frame (is this usually called the World frame?) Then, you have position vectors (well, the points in the main frame) which locate the tail of the line of sight vector.
Do you use different frames? Like perhaps one for the line of sight vector, and perhaps one for the normal to the facet?
Then, you'd have to come up with the normal to each n-1 facet of the nD polytope. Presumably, you take the one pointing outward. Can you tell whether it's pointing inward or outward by... well, something perhaps to do with the parametric equations of the rays of one of the position vectors of a corner of the facet and the normal... They won't intersect, but can the range, or sign, of something... Seems to me I've seen this done sometime. Somehow I think you can tell whether the two vectors are pointing in the same direction...
Perhaps you'd use the wedge product that represents the planar hypervolume of the facet? But, that's just an orientation... no. I think you need to compare it to a 1-vector...?
Anyway... Once you've got the normal pointing outward (I'd think that would be the better...) then if you calculate the angle of incidence between the normal and a ray from the line of sight intersecting the normal... perhaps this angle of incidence would reveal if the facet is visible from the line of sight?
Anyway... how do you do this?
That applet doesn't work in IE for me... it does work in Netscape, though... Do you need the Sun Java enabled?
Anyway... I'm not sure I understand. Is that a 3D cube and a 3D tetrahedron in the applet?
Also...
- Code: Select all
if ( this.offset < 0 ) {
this.normal = new Point4D( -e234, e134, -e124, e123 );
this.offset = this.normal.dot( aa );
}
This part of your code looks like it might be taking the negative of some vector. Is it taking the negative of the normal if it turns out that we get the one pointing towards the centroid of the polytope?
Also... this hidden line stuff... Is the centroid of the polytope at the origin, at least of the main frame (is this usually called the World frame?) Then, you have position vectors (well, the points in the main frame) which locate the tail of the line of sight vector.
Do you use different frames? Like perhaps one for the line of sight vector, and perhaps one for the normal to the facet?
Then, you'd have to come up with the normal to each n-1 facet of the nD polytope. Presumably, you take the one pointing outward. Can you tell whether it's pointing inward or outward by... well, something perhaps to do with the parametric equations of the rays of one of the position vectors of a corner of the facet and the normal... They won't intersect, but can the range, or sign, of something... Seems to me I've seen this done sometime. Somehow I think you can tell whether the two vectors are pointing in the same direction...
Perhaps you'd use the wedge product that represents the planar hypervolume of the facet? But, that's just an orientation... no. I think you need to compare it to a 1-vector...?
Anyway... Once you've got the normal pointing outward (I'd think that would be the better...) then if you calculate the angle of incidence between the normal and a ray from the line of sight intersecting the normal... perhaps this angle of incidence would reveal if the facet is visible from the line of sight?
Anyway... how do you do this?
- Paul
- Trionian
- Posts: 74
- Joined: Sat Sep 04, 2004 10:56 pm
Paul wrote:That applet doesn't work in IE for me... it does work in Netscape, though... Do you need the Sun Java enabled?
Hmmm... don't know... it may require Java 1.4, but I didn't knowingly use anything from 1.4.
Anyway... I'm not sure I understand. Is that a 3D cube and a 3D tetrahedron in the applet?
No, those are the visible facets of a hypercube and a tet. The facets themselves are 3-d cubes and tetrahedrons. But, there's often more than one facet visible. You'll have to rotate with the second mouse button (or shift+first-button) to see more than one facet at a time.
- Code: Select all
if ( this.offset < 0 ) {
this.normal = new Point4D( -e234, e134, -e124, e123 );
this.offset = this.normal.dot( aa );
}
This part of your code looks like it might be taking the negative of some vector. Is it taking the negative of the normal if it turns out that we get the one pointing towards the centroid of the polytope?
Yep, when you calculate the normal to a plane, it doesn't matter to the plane whether you pick a normal that's pointing away from one side of the plane or away from the other. In my case, however, I want all of my normals to point away from the origin. So, if the offset had turned out negative, I would want to flip the normal... and use the one that points away from the origin. It just makes my visibility calculations later easier if I know all of my normals point away from the origin.
Also... this hidden line stuff... Is the centroid of the polytope at the origin, at least of the main frame (is this usually called the World frame?) Then, you have position vectors (well, the points in the main frame) which locate the tail of the line of sight vector.
Do you use different frames? Like perhaps one for the line of sight vector, and perhaps one for the normal to the facet?
I'm not sure what you mean by different frames. The calculations going on here are this. I have placed the object at the origin. I have picked a point four units away (and a little to the left for the left eye and a little to the right for the right eye) to be the viewpoint. I then determine which vertexes of the object are visible from the viewpoint (At this point, I have not rotated the vertexes at all, I've just checked to see if the line segment from the vertex to the viewpoint intersects any of the facets of the polytope). Then, I go through all possible pairs of vertexes that were visible and check to see which of them have an edge between them. If they have an edge between them, then I determine where the vertexes will appear on the screen and draw a segment between them.
To decide where a vertex appears on the screen, I rotate it based on the its orientation to the viewpoint that was used for clipping. Before, when I checked the visibility, I did this without rotating. For this, I'm rotating so that the viewpoint is effectively where you are sitting... back from the screen a bit. Then, I also rotate it based upon how you have moved the third mouse button (assuming you still have the third mouse button pressed). This doesn't result in any new determination of which vertexes are visible. It just lets you look around a bit more. Then, I translate the vertex a bit to account for the distance from the clipping viewpoint to the origin. I now have the coordinates of this object relative to the viewpoint's world. I then project down to three dimensions by lopping off the w-coordinate. I then project down to two dimensions by doing a perspective calculation (dividing the horizontal and vertical offsets by the distance away the vertex is).
Then, you'd have to come up with the normal to each n-1 facet of the nD polytope. Presumably, you take the one pointing outward. Can you tell whether it's pointing inward or outward by... well, something perhaps to do with the parametric equations of the rays of one of the position vectors of a corner of the facet and the normal... They won't intersect, but can the range, or sign, of something... Seems to me I've seen this done sometime. Somehow I think you can tell whether the two vectors are pointing in the same direction...
I only determine the normals of the planes once at the beginning of setting up the Tet. For the cube, I don't have to calculate the normals, they're pretty easy to just "know". If the dot-product (inner-product, scalar-product) of two vectors is positive, then they generally point in the same direction. If it is negative, they generally point in the opposite direction. That's what that step in the code you quoted was about. If the dot product of my candidate normal with a vertex in the plane came out negative, that indicates that the vector from the origin to the vertex points somewhat opposite the direction of the normal. I don't want this, so I flip the normal.
For completeness, if a and b are vectors, then if a.b = |a|*|b|, then the vectors point exactly the same direction. If a.b = -|a|*|b|, then the vectors point in exactly opposite directions. The dot product cannot get any bigger or smaller than that.
Anyway... Once you've got the normal pointing outward (I'd think that would be the better...) then if you calculate the angle of incidence between the normal and a ray from the line of sight intersecting the normal... perhaps this angle of incidence would reveal if the facet is visible from the line of sight?
Yes, but in this case, I'm concerned with which vertexes are visible from the line of sight. Fortunately, in the case of the Tet, the only surface that can hide a vertex is the (unique) surface that does not contain that vertex. So, I have to check that the viewpoint is below (on the origin side of) all of the hyperplanes which contain the point *and* that the viewpoint is above (on the side opposite the origin of) the hyperplane which does not contain the vertex. If all of those are true, then the vertex is hidden from the viewpoint by the facet opposite the vertex.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
26 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 17 guests
