More precisely, the type I'm referring to are fractals which are self-similar in the following way:
- One can approximate the fractal iteratively
- Each iterant is some number of displaced, shrunken copies of the previous iterant such that:
- All copies are scaled down by the same amount
- The interiors of the copies are disjoint (the copies don't overlap)
- Each copy is contained within the volume of its parent iterant
The Koch snowflake is not such a shape, the iterants increase in volume.
The Menger sponge has easy analogues in any number of dimensions. Take the unit n-cube as the zero-th iterant. Set up a coordinate system for the cube with the origin at the center of the cube and the axises normal to the faces ( (n-1)-facets). Then, divide the cube into thirds along each axis. Throw away all cubes which touch an axis. Lather, rinse, repeat on each remaining subcube. This is equivalent, in my above parlance, of taking 3<sup>n</sup> - 2n - 1 copies of an iterant, each 1/3-rd the original size and displacing them appropriately along the edges ( (n-2)-facets ).
Interestingly, there is an easy way to calculate the Hausdorff dimension of fractals of this type (even without the restriction that the k+1-th iterant is contained in the volume of the k-th iterant). For the Menger sponge in n dimensions, the Hausdorff dimension will be log<sub>3</sub>( 3<sup>n</sup> - 2n - 1 ). Interestingly, as $n$ gets large, the Hausdorff dimension of the n-dimensional Menger sponge approaches $n$.
I started implementing this type of fractal in my raytracer (but, I haven't uploaded the code yet because right now, you can't do the intersection of these fractals with other shapes). I haven't run 4-dimensional Menger sponges yet. But, I did run a similar fractal that I'm calling the cross-sponge.
Iterant zero is a cross-polytope. The next iterant is 2n copies of iterant zero, scaled down by a factor of one half and displaced so that the bounding polytope of the set of copies is exactly iterant zero (basically, just pushing copy k out until it touches the k-th vertex of iterant zero). This shape has fractal dimension log<sub>2</sub>(2n). In particular, for the case where n=1, the fractal dimension is 1... it fills the line. For the case where n=2, the fractal dimension is 2... it fills the plane. After that, it falls behind fast:
3-d: dim 2.584962500721156
4-d: dim 3
5-d: dim 3.3219280948873626
6-d: dim 3.5849625007211565
7-d: dim 3.8073549220576037
8-d: dim 4
Here's a pic of the 6-th iterant of the three-dimensional version:

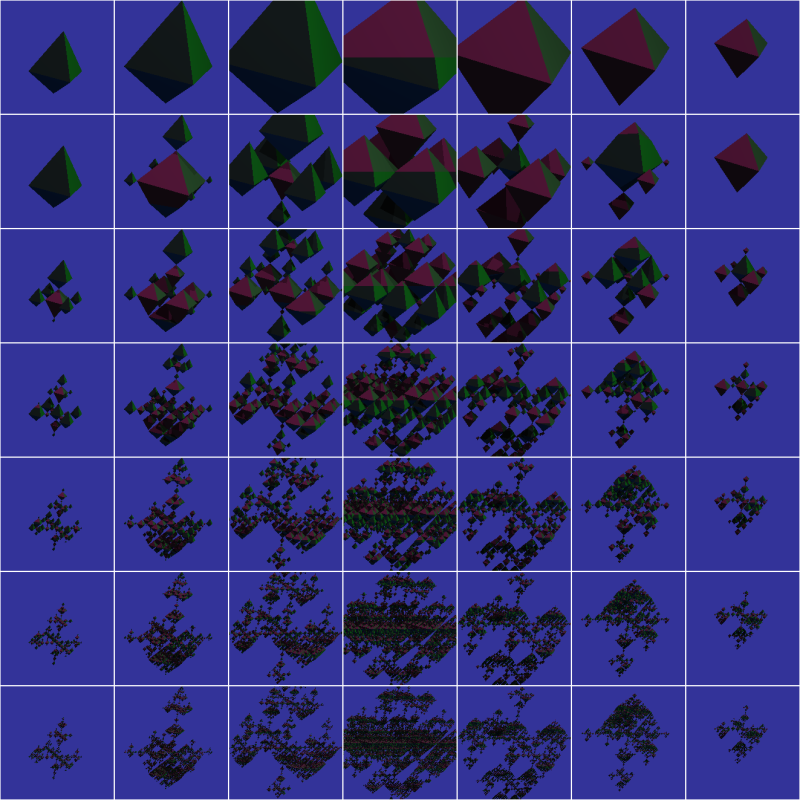
And, here are successive iterants of the four-dimensional version. The top row is the zero-th iterant, the bottom row is the sixth iterant.