Can there be a continuous transform between spaces with different numbers of dimensions? Strictly, no. In the limit, yes.
There are two main models for dimensions. Straight lines and circles. Each is a limiting case of a spiral. A spiral with no pitch is a straight line while a spiral with increasing pitch has as its limit a complex plane.
The transform one could use would be multiplying by a complex number. If the number is real then you get a straight line. If imaginary you get a circle. Anything in between is also possible. There you go, a continuous transform between a circle and a straight line, simple as could be. If you want to completely get rid of a dimension, shrink that circle to a point. That complex number becomes zero. Reverse the process to grow a dimension from a point.
This system is centered around a point, not coordinate-free. But special relativity is point centered too. Chemists who do calulations have to keep separate dimensions for every particle. If they have 25 particles they are working in a 100 dimensional space. This is why quantum computers are important: only they are practical for calculations in such spaces.
Morphing between dimensional spaces
5 posts
• Page 1 of 1
Re: Morphing between dimensional spaces
Well, the quantum number system will allow you to create completely new projects. Perhaps this would allow us to make a scientific breakthrough, create new technologies that will simplify our life, allow us to plan space travel, and help create a formula for a particularly powerful fuel. This is, of course, reasoning. But who knows?
- Challenger007
- Dionian
- Posts: 32
- Joined: Thu Nov 12, 2020 2:51 pm
Re: Morphing between dimensional spaces
There are some interesting issues here.
1. The idea of 'identity'. You look at a cartoon and see say, 'donald duck' there. But it's just different parts of the paper are coloured differently, and we have been trained to see things like animals -> animaloids -> ducklike things -> donald duck. But he is as much part of the fabric as anything else is on the page.
So if we imagine ourselves as 'slipping into four dimensions', what is happening is that the like of 'donald duck' standing up from the page and adding an extra dimension. It is easier for dd to do this, because he is already a presentation of 3d, and we might imagine that the cartoon is but a window into a different world. Then DD can wander out of the frame and talk to us.
2. We are already three-dimension and not a representation of four dimensions, and thus we have no form in four dimensions.
3. One of the other meanings of 'dimension' is a parallel world. These exist if you suppose something like Stargate or Dr Who, where it is possible to leave something that looks like London and end up in something that looks like Lhasa. No higher dimensions, just doors to different 3d realities.
1. The idea of 'identity'. You look at a cartoon and see say, 'donald duck' there. But it's just different parts of the paper are coloured differently, and we have been trained to see things like animals -> animaloids -> ducklike things -> donald duck. But he is as much part of the fabric as anything else is on the page.
So if we imagine ourselves as 'slipping into four dimensions', what is happening is that the like of 'donald duck' standing up from the page and adding an extra dimension. It is easier for dd to do this, because he is already a presentation of 3d, and we might imagine that the cartoon is but a window into a different world. Then DD can wander out of the frame and talk to us.
2. We are already three-dimension and not a representation of four dimensions, and thus we have no form in four dimensions.
3. One of the other meanings of 'dimension' is a parallel world. These exist if you suppose something like Stargate or Dr Who, where it is possible to leave something that looks like London and end up in something that looks like Lhasa. No higher dimensions, just doors to different 3d realities.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Morphing between dimensional spaces
wendy wrote:There are some interesting issues here.
1. The idea of 'identity'. You look at a cartoon and see say, 'donald duck' there. But it's just different parts of the paper are coloured differently, and we have been trained to see things like animals -> animaloids -> ducklike things -> donald duck. But he is as much part of the fabric as anything else is on the page.
So if we imagine ourselves as 'slipping into four dimensions', what is happening is that the like of 'donald duck' standing up from the page and adding an extra dimension. It is easier for dd to do this, because he is already a presentation of 3d, and we might imagine that the cartoon is but a window into a different world. Then DD can wander out of the frame and talk to us.
2. We are already three-dimension and not a representation of four dimensions, and thus we have no form in four dimensions.
3. One of the other meanings of 'dimension' is a parallel world. These exist if you suppose something like Stargate or Dr Who, where it is possible to leave something that looks like London and end up in something that looks like Lhasa. No higher dimensions, just doors to different 3d realities.
But your thoughts are quite logical and, in principle, obvious, only you catch yourself thinking that you cannot formulate them correctly or simply come to such a conclusion. Well, simply because such things seem obvious and, as it were, do not need to be formulated.
- Challenger007
- Dionian
- Posts: 32
- Joined: Thu Nov 12, 2020 2:51 pm
Re: Morphing between dimensional spaces
I’ve always felt that Visual Reorientation Illusions (VRIs) allow one to morph between dimensional viewpoints of the same space.
Something like the Necker Cube Illusion, but instead of seeing only a perceived 2D figure flipping to different 3D viewpoint angles, you get to see our perceived 3D surroundings flip to different 4D viewpoint angles.
When one unfolds a 4D tetracube you get all these different 3D cubes.
When the tetracube is all folded up, each cube is still in there with its own 3D viewpoint, and the lines in this pic show the pathways of morphing between them.
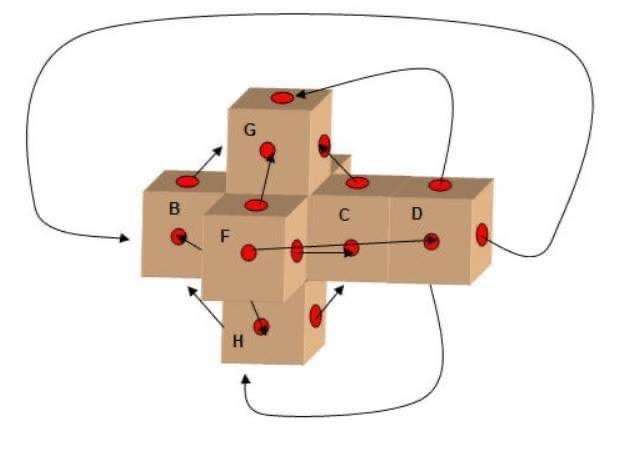
Something like the Necker Cube Illusion, but instead of seeing only a perceived 2D figure flipping to different 3D viewpoint angles, you get to see our perceived 3D surroundings flip to different 4D viewpoint angles.
When one unfolds a 4D tetracube you get all these different 3D cubes.
When the tetracube is all folded up, each cube is still in there with its own 3D viewpoint, and the lines in this pic show the pathways of morphing between them.


My VRI channel: http://youtube.com/channel/UCntWMVVl5wKCx_6CH33_mXg
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
5 posts
• Page 1 of 1
Return to Higher Spatial Dimensions
Who is online
Users browsing this forum: No registered users and 35 guests
