Traversable Klein 'bottle' paths

[Teragon]

I realise, looking at this again, that there is definitely one error to correct so far...
I'll try changing the equations tomorrow to:
x(u,v,s,t) = (R + r * cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * -sin(v/2) + cos(u + t) * cos(v / 2))) * sin(v * cos(s * cos(t)))
y(u,v,s,t) = (R + r *cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * -sin(v/2) + cos(u + t) * cos(v / 2))) * cos(v * cos(s * cos(t)))
z(u,v,s,t) = r * cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * cos(v/2) + cos(u + t) * sin(v / 2))

What is "s" there?

In case it helps, these should be the parametric equations for the whole objects:

90°-Moebius-spheritorus:
x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(u/2)*cos(v)
w = t*sin(u/2)*cos(v)

0°-Moebius-spheritorus:
x = sin(u)*(R + t*sin(u/2)*sin(v))
y = cos(u)*(R + t*sin(u/2)*sin(v))
z = t*cos(u/2)*sin(v)
w = t*cos(v)

u, v = [0, 2pi]
w = [0, r]

Awesome Teragon . I'm pleased to hear that you are also making this for our solid objects in 4D! I look forward to seeing that .

You have to be patient though. It's something I'm gonna spend some time on now and then, so it's going to take a longer timespan.

Maybe one day you can also help me to create a program to show 4D objects using my rotated projection model. That's something I hope to make one day.

Oh I hope so. Do you think the mathemtical part or the programming part is gonna be more difficult for you?

These colour versions make clearer sense to me now, cool! I guess that is the process of my brain adapting to new models?

Sure. You're learning to orient yourself in this new world

Considering the animation of the 3D Klein strip in 4D I think it's much easier to get it right and internalize it using an actual 3D image. Are you familiar with the cross-eyed-view?
It's just a matter of practice. You are squinting at the pictures, a bit like you wanted to look at your nose, or like looking through everthing, so you see both images twice. You vary the degree your eyes cross, until the inner two images are congruent. Then you can easily focus onto this new image in the center and it's gonna be in 3D.



I did a rotation in the wz-plane as well (it's a bit more tricky to see the flips here):

The 90°-object is the more symmetric one, as all the directions the surface normal points at look identical. The surface normal is always pointing ouside of the loop. It just came to me that this means that you could rotate the object in the plane of the loop by some angle, then rotate it by the same angle in the plane perpendicular to the plane of the loop and retain the exact same shape! That means in the same way a torus has a rotational symmetry (=invariance under rotations), the 90°-Moebius-Spheritorus has a double-rotational symmetry (=invariance under double rotations).

I might need you to explain this a bit more please Teragon.

Which are the concepts here you don't understand?

[gonegahgah]

This rotation using cos and sin is seemingly getting frustrating for what I'm trying to do...
I've been able to do what I wanted to do but only on a donut and a pinched torus.
I'm struggling to translate it to a rotated pinched torus (the Klein Ring 3D middle slice).

Here are my results at the moment:


They show the effect but aren't the right shapes...
The pinched torus is closest but it lacks the essential rotation and changing between a Mobius and a fat back.
A pinched torus is easily created by reducing the donut height only via *cos(v/2) where v steps us around the ring.
My present aim is to animate a 3D slice showing us twisting the back of the Klein Ring into 4D space.
Just like we twist a Mobius Strip although it only twists left or right in our 3D.
The twisting is meant to then show a 4D showing us the various Klein varieties that are available.

I'm beginning to wonder at the math!
So far for the rotating donut I have for the red and yellow parts:
x= (2 * cos(u * (cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +1.57079632679) + 6) * -sin(v)
y= (2 * cos(u * (cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +1.57079632679) + 6) * -cos(v)
z= (2 * sin(u * (cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +1.57079632679))
and for the blue and green parts:
x= (2 * cos(u * (1- cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +0) + 6) * -sin(v)
y= (2 * cos(u * (1- cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +0) + 6) * -cos(v)
z= (2 * sin(u * (1- cos(v/2)^2 * (2-sin(t)^2)/2) + t * cos(v/2) +0))
Yellow adds: 4.71238898038. Green adds: 3.14159265359.
All are based upon: -π/2 ≤ u ≤ π/2, 0 ≤ v ≤ 2π, -4π ≤ t ≤ 4π
There must be some way to reduce the similar ones (red and yellow | blue and green) to common equations?

The old Klein Strip has the following formula:
(2 * (sin(v/2) * cos(u + t) - cos(v/2) * sin(u + t) * cos(t) * cos(v/2)) + 6) * sin(v)
(2 * (sin(v/2) * cos(u + t) - cos(v/2) * sin(u + t) * cos(t) * cos(v/2)) + 6) * -cos(v)
(2 * (cos(v/2) * cos(u + t) + cos(v/2) * sin(u + t) * cos(t) * sin(v/2)))

How do I successfully marry the two???

[gonegahgah]

I'm learning math again Hopefully with even more understanding.

So we start thinking about drawing on a rectangle like the following to begin:

We can derive the formulas from this...

1) Make rectangular picture:
a_r= u * ( cos(v/2)²*(2-sin(t)²)/2 ) + t * ( cos(v/2) ) + 0
a_y= u * ( cos(v/2)²*(2-sin(t)²)/2 ) + t * ( cos(v/2) ) + π
a_g= u * ( 1-cos(v/2)²*(2-sin(t)²)/2 ) + t * ( cos(v/2) ) + π/2
a_b= u * ( 1-cos(v/2)²*(2-sin(t)²)/2 ) + t * ( cos(v/2) ) + 3π/2
2) Turn rectangle into cylinder:
hor = r * cos(a)
vert = r * sin(a)
3) Turn cylinder into donut:
x = (hor + R) * -sin(v)
y = (hor + R) * -cos(v)
z = (vert)

It now seems apparent to me that I can't escape the fixed inserted values for this representation as each section acts separately.



The following are just working notes... I'll delete them soon:

[Teragon]

Can't follow the logic of what you're doing right now.
Do you just want to make an animation showing a smooth transition between both extremes of Moebius strips for a constant slice? Isn't that what you've already done?

[Teragon]

I'm not able to make projections of the full Moebius tori in 4D yet, showing the interior of their 3-surface and the proper shading, but what I can show is a projection of their edge, shading it like a 3D-object. We have to be aware that the actual objects' surface is solid in this projection. As usual red is closer in w, blue is further away.

Moebius-0°-spheritorus
Rotating in yw


Rotating in zw


Moebius-90°-spheritorus
Rotating in yw


Rotating in zw

The last animation expresses nicely what I was trying to convey about the symmetry of this object. As the object rotates in the zw-plane it looks the same as if it was rotating in the xy-plane! If it would rotate in the zw-plane and the xy-plane simultanisously (double rotation) in the appropriate sense of rotation, its visual appearance would not change at all. In other words: It has a symmetry with respect to double rotations.

A symmetry of an object corresponds to an operation acting on it (rotation, mirroring, inversion...) that leaves its shape invariant.

I have also made some adjustments for the 3D Moebius strip above. The distance of the object to the observer was very small, in reality you couldn't focus onto the whole object. I've made it larger, now it really looks more like a rotation, because the changes in size between closest and furthermost point are more natural.

[gonegahgah]

Can't follow the logic of what you're doing right now.
Do you just want to make an animation showing a smooth transition between both extremes of Moebius strips for a constant slice? Isn't that what you've already done?

Sorry, I'm using similar colours to your model which is probably confusing things plus it does need an explanation.
I believe the overall shape is fairly representative (though I'm wondering if it can and/or should be or not be reduced to a direct transition equation rather than additive equation).

What I'm looking to produce here is still a 3D slice representation.
This time I realised that I want to try and give a greater sense of the true rotational differences between the Klein Ring varieties.
So, I've gone back to the Mobius Strip analogy of a cut piece of paper.
We turn a cut ribbon of paper into a Moebius Strip by twisting each end a quarter turn each and reconnecting around at the back of a ring.
Throughout the process the front doesn't change orientation; only the back wall (or you could put the twist at the front path or anywhere but I chose the back wall for greater visual effect).
The paper ribbon won't give us a perfect Moebius Ring but it gives the idea.

So, I've taken that idea and added it to our Klein Ring.
The animation I made shows the ring twisted through our space and through 4D space. It remains twisted throughout the animation but the twist changes orientation.
To make the animation have longer presence I've twisted the back wall part several times while keeping the back upright.

The result then is as per earlier modelling that I did on here:


Hmm, just realised something... I'll try to rethink and remodel it...
Hmm, but come to think of it; the pattern is correct, the problem is with the canvas.
That is the torus canvas and the pinched torus canvas produce the visual error. This is an error of not just the shape but of the transition from one path orientation to another.
If I can create a proper Klein Ring canvas then this will be automatically corrected.

I'll redo the above images to show more what I am meaning by my new pattern and explain it more then...

I'm taking the similar approach to the following:

Usually we would paint one apparent side as one colour and the second half (underneath) as another colour.
Instead I am imbuing one apex half as one colour and the other half as another colour.
By imbuing I can just refer to the orientation instead of the surface.
I can say the red apex is on the left and blue on the right; or vice versa if it is twisted the other way around.

So I'm doing a similar thing with the Klein Ring:

I've imbued a quadrant of each path cross-section in one of four colours so that we can see the change in orientation of the path as it circles the Klein Ring.
If any two opposite quadrants of the Klein Ring are fully off in 4th space we can't can't see them and instead only see the colour at that cross-section for the other two opposite quadrants.
We get to see more or less of particular quadrants as the back is rotated to different orientations.

[gonegahgah]

I redid the the following images to match the evidence presented by the animation following:

I'm calling the left image 0° and the right image 90° in line with your having the Klein variety as the 0° variety Teragon.

The following is a combination of the self-rotating image on a pinched torus:


It's not quite where I want to get yet but it shows one thing that I at first thought was a bug but I'm starting to think that it is a feature!
It seemingly appears that two of the opposite axis only swap sides (blue to green, green to blue)?
The other two seem to stick to their own axis (red to red, yellow to yellow).

I guess if I was going to relate this to anything it is that we end up attaching mirror images of the ends to each other.
Which seems to be the 4D thing when you rotate anything through 4th space.
So it might just be right?

Does anyone feel that it is not right?
I updated the equations again to make the animation congruent with the images:
1) Make rectangular picture:
... a_r= u * ( cos(v/2)²*(2-sin(t)²)/2 ) + π/2
... a_y= u * ( cos(v/2)²*(2-sin(t)²)/2 ) + 3π/2
... a_g= u * ( 1-cos(v/2)²*(2-sin(t)²)/2 ) + 0
... a_b= u * ( 1-cos(v/2)²*(2-sin(t)²)/2 ) + π
2) Give Klein like twist to the picture:
... a = a - t * cos(v/2)
3) Turn rectangle into cylinder:
... hor = r * sin(a)
... vert = r * cos(a)
4) Turn cylinder into torus:
... x = (hor + R) * -sin(v)
... y = (hor + R) * -cos(v)
... z = (vert)
5) Turn torus into pinched torus:
... z = z * cos(v/2)
(I call step 1 the picture and steps 2-5 the canvas).

Some still images for comparison:



I currently have the rotation in the image itself. Hopefully I can put the rotation instead in a Klein Ring canvas; if that is possible?

[Teragon]

Usually we would paint one apparent side as one colour and the second half (underneath) as another colour.
Instead I am imbuing one apex half as one colour and the other half as another colour.
By imbuing I can just refer to the orientation instead of the surface.
I can say the red apex is on the left and blue on the right; or vice versa if it is twisted the other way around.

But in order to know which way the band is twisted you need the additional information, if the blue is on the top or on the bottom half on the opposite side and which way you color from there. Also the coloring is unambiguous, there are different ways to color one and the same object - it's gonna be tricky to extract the actual information about the object from that depictions. Terms like "left" and "right" are dependend on the point of view and thus inconvenient tools for commucation. Anyway I wonder why you are bothering about different senses of rotation - it's just a matter of the point of view - when you're looking from ana it's twisting to the left, when you look from kata it's twisting to the right.

Why do you let blue go from w to -z and red from y to -w, instead of keeping blue at w and just moving red from y to -z? It shows the simple rotation the surface does much nicer.

This is made more complicated than it is.

Huh?

It's not quite where I want to get yet but it shows one thing that I at first thought was a bug but I'm starting to think that it is a feature!
It seemingly appears that two of the opposite axis only swap sides (blue to green, green to blue)?
The other two seem to stick to their own axis (red to red, yellow to yellow).

This observation is absolutely correct. That's what a rotation of an n-surface is! You've got a surface extented in n-1 directions and one direction pointing away from the surface (the surface normal). Rotation by 180° means that the roles of the surface normal and one direction of the surface change, but the rest of the directions remain the same (the other lateral direction and the direction along the torus in this case). If another direction would also flip, the object would have to be turned inside out.

This is the 90° object with the coloring of the 0° object.

[...]
Does anyone feel that it is not right?

I hope you will undertand that I don't have the time to follow all your considerations. It's an ambitious project that takes a lot of considerations. My advice would be to first learn enough about 4D geometry using established and well documented approaches, so that you can apply those tools to new objects and you know much faster if you're on the right track and what you have to do in order to reach your goal. I would be more effective.

[gonegahgah]

[Moved this to a following post...]

[gonegahgah]

But in order to know which way the band is twisted you need the additional information, if the blue is on the top or on the bottom half on the opposite side and which way you color from there. Also the coloring is unambiguous, there are different ways to color one and the same object - it's gonna be tricky to extract the actual information about the object from that depictions. Terms like "left" and "right" are dependend on the point of view and thus inconvenient tools for commucation. Anyway I wonder why you are bothering about different senses of rotation - it's just a matter of the point of view - when you're looking from ana it's twisting to the left, when you look from kata it's twisting to the right.

The left-right is in reference to the Moebius as an analogous example. The main thing was that I wanted to refer to 4 opposite/perpendicular circumference points in the circle cross-section of the Klein Ring.

Why do you let blue go from w to -z and red from y to -w, instead of keeping blue at w and just moving red from y to -z? It shows the simple rotation the surface does much nicer.

Keeping w at w (from front pinch to back) and rotating y to z describes the 0° variety. Moving w to y and y to z from front to back describes the 90° variety.
If we take the back as having only a z and no y at 0° then if we rotate the z to y we will end up with a y and no z. The back will then have no height and we won't have a Klein Ring any more.
We'll instead be going from w y at the front to w y at the back which isn't a Klein Ring. So the dual rotation is fundamental.
Doing it the way you mention would be changing it from a Klein Ring variety at 0° to an ordinary Torus at 90°.

[Edit: Hmm, apologies Teragon, you could do that. You could move any point along the edge at the front circle cross-section up to z. I didn't realise that.]
[The characteristic Moebius like bump should remain. Does that make the equations easier to make I wonder?]

I have noticed an error in my canvas though. The following line simply creates a valley instead of the desired consistent slide.
2) Give Klein like twist to the picture: ... a = a - t * cos(v/2)
My work in progress should fix that up hopefully... I'm curious to see what effect it has on the 'feature'.

I apologise for the learning process but I think I am on the right track...

[Teragon]

Keeping w at w (from front pinch to back) and rotating y to z describes the 0° variety. Moving w to y and y to z from front to back describes the 90° variety.

The simplest description of the 0° variety is y going to z and w staying at w.
The simplest description of the 90° variety is w going to z and y staying at y.
How you've colored the 0° variety is y going to w and w going to z.
How you've colored the 90° variety is w going to y and y going to z.
The proof is in your own figures.

[gonegahgah]

The simplest description of the 0° variety is y going to z and w staying at w.
The simplest description of the 90° variety is w going to z and y staying at y.
How you've colored the 0° variety is y going to w and w going to z.
How you've colored the 90° variety is w going to y and y going to z.
The proof is in your own figures.

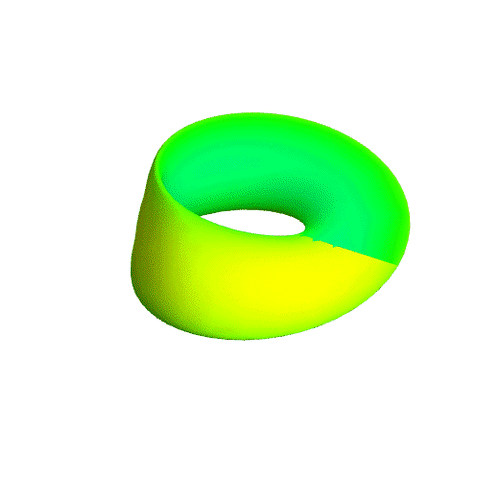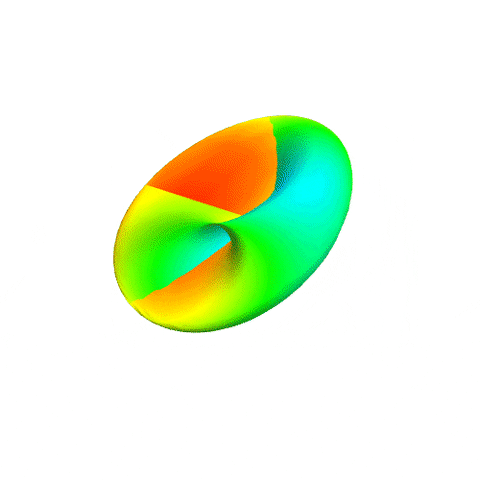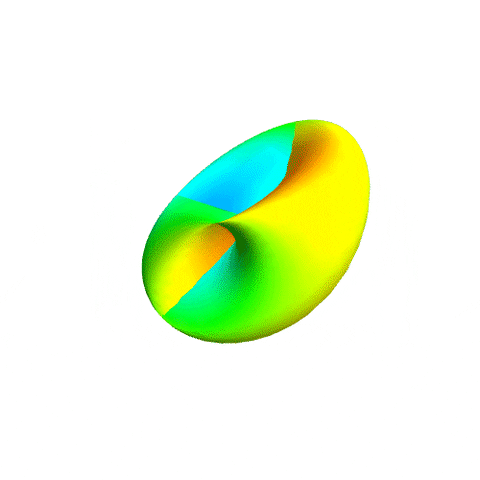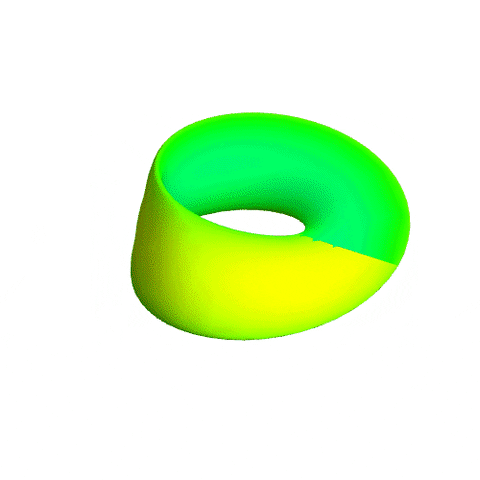
Must have been reading your thoughts I was just making an apology above...

I've just been making some changes to my equations to change it to:
-π/2 ≤ u ≤ π/2, -π ≤ v ≤ π, 0 ≤ t ≤ ?
Next I'll change the way it rotates to make it easier to then add the correct squishing last of all...

You asked before if my go was mathematics or programming.
I always had an interest in geometry especially at school for some reason.
However, I've mainly spent my time programming.

The following changes went extremely well
[I cut the following from my work-in-progress from above...]
1) Make rectangular picture:
... a_r=a_y= u * ( 1-(1-cos(v/2)^2)*(2-sin(t)^2)/2 )
... a_g=a_b= u * ( (1-cos(v/2)^2) * (2-sin(t)^2)/2 )
2) Turn rectangle into radian sized cylinder:
... hor_r = cos(a_r), vert_r = -sin(a_r)
... hor_g = -sin(a_g), vert_g = -cos(a_g)
... hor_y = -cos(a_y), vert_y = sin(a_y)
... hor_b = sin(a_b), vert_b = cos(a_b)
3) Give Klein like twist to the cylinder:
... hor' = hor * cos(t*sin(v/2)) - vert * sin(t*sin(v/2))
... vert' = vert * cos(t*sin(v/2)) + hor * sin(t*sin(v/2))
4) Turn cylinder into full sized torus:
... x = (r * hor + R) * -sin(v)
... y = (r * hor + R) * -cos(v)
... z = (r * vert)
5) Turn torus into pinched torus:
... z = z * cos(v/2)
[I've made alterations to the above to reduce redundancy]

The result looks exactly like before so there is nothing new to show yet despite the rejigging.
It should make it possible for me to add the rotated squishing I wish to add between steps 2 and 3...

... and now, looking at this, I realise I shouldn't have changed to having the Moebius variety at 0°.
It's appears to be quite simple to add the pinch but only if I had kept the varieties where they were!
I'll have to go back through the formulas and change them by 90°. Ah well, back we go...

[gonegahgah]

Thank the math gods I only had to change the rectangular picture to:
... a_r=a_y= u * ( 1-(1-cos(v/2)^2)*(2-cos(t)^2)/2 )
... a_g=a_b= u * ( (1-cos(v/2)^2) * (2-cos(t)^2)/2 )

I was hoping to get rid of step 5 and just add in the following:
2c) Squish the cylinder for the various Klein varieties:
... ver_sq = ver * sin(v/2)*cos(t)

but I can forsee a problem with that... Hmmm?

...or perhaps not. The changes did work and produce the following:

This presently goes from 0 ≤ t ≤ 4π so I'm giving it a good 4 whole twists there!

I'm confident that it is probably not 100% correct yet.
It does have some nice features like the green and blue swapping front and back as the green and blue edges change places relative us.
It is even possible that physically twisting the Klein Ring back will produce those unexpected undulations as the bulk rotates relative to us?
Or can someone tell me if twisting is not possible in 4D? ie. Does it automatically undo itself? I suspect not but tell me if it is otherwise please?
I'll have to explore it more too... There has to be a Moebius Strip at the heart of it I'm fairly confident and hopeful!

The following was an interesting attempt at a partial fix:


I figured that we should see some sort of figure 8 rotation which I think is right.
But, I would hope that this is not it.
I would instead want to see the visible bulk rotate fully around like before.
I'm thinking that is what would happen?
I do want to see the two back halves with a different orientation to each other which isn't present in these.
That is a return to the more Moebius shape. I'm still hoping that is the correct shape?
I'm also suspicious that the clumping is a normal artifact of twisting.
If we over-twist a Moebius Strip it will form clumping too, but it is a line path not a circle?
But, it may be that this is just how the visible bulk orientation appears to us?
So, hence my question about whether it is possible to twist in 4D or does twisting not really exist?

I did the above attempt by changing step 3 to:
3) Give Klein like twist to the cylinder:
... hor' = hor * cos(sin(t)*sin(v/2)) - vert * sin(sin(t)*sin(v/2))
... vert' = vert * cos(sin(t)*sin(v/2)) + hor * sin(sin(t)*sin(v/2))

The next attempt is most certainly a fail too:


I did this one by changing step 3 to:
3) Give Klein like twist to the cylinder:
... hor' = hor * cos(t*sin(v/2)²) - vert * sin(t*sin(v/2)²)
... vert' = vert * cos(t*sin(v/2)²) + hor * sin(t*sin(v/2)²)

I can see now that I shouldn't be varying the rotation of the shape; the bellows effect needs to be in just one rotated plane...
I can put the rotation back then at the picture level I suspect...

[gonegahgah]

Finally got the animation result to where I want it to be!


At the present time the equations are:
1) Make rectangular picture:
... ar=ay= u * ( 1-(1-cos(v/2)²)*(2-cos(t)²)/2 )
... ag=ab= u * ( (1-cos(v/2)²) * (2-cos(t)²)/2 )
2) Rotate picture over time:
... b= a + t*sin(v/2)
3) Turn rectangle into radian sized cylinder:
... horr = cos(ar), vertr = -sin(ar)
... horg = -sin(ag), vertg = -cos(ag)
... hory = -cos(ay), verty = sin(ay)
... horb = sin(ab), vertb = cos(ab)
4) Squish the cylinder for the various Klein varieties:
... versq = ver * sin(v/2)*cos(t)
5) Give Klein like twist to the cylinder:
... hor' = hor * cos(π*sin(v/2)²) - vert * sin(π*sin(v/2)²)
... vert' = vert * cos(π*sin(v/2)²) + hor * sin(π*sin(v/2)²)
6) Turn cylinder into full sized torus:
... x = (r * hor + R) * -sin(v)
... y = (r * hor + R) * -cos(v)
... z = (r * vert)

I do suspect something is wrong still because when we connect cross section edge points:
... 1/3 to 3/1 at top bottom then should be 2/2 & 4/4 at front back,
when we connect:
... 2/4 to 4/2 at top bottom then should be 1/1 & 3/3 at front back...

That's not quite the result presently?

Funnily, to me at least, I just realised that my bulk rotation was going the opposite way to the colour flow...
So I've fixed that by changing the π's to -π's as per the new animation below:


But, more hilarious, that still doesn't fix the problem. I'm starting to consider what might be going on...

It leaves the following as a possibility:
[XXX WRONG XXX]

Which kind of gives me some feeling of actually making sense...
That will be interesting to try to draw!

But, I'm not certain that can be right either? You can't have G-Y & R-B opposite pairings can you? I wouldn't think that was possible.
There is another interesting possibility? I'll explore it tomorrow...

This seems to be the strange and interesting path of the four perpendicular or opposite sides of the cross-section of a Klein Ring.
[XXX WRONG XXX]

By path I mean that the final orientation for one side at the back (say left) changes between these orientations to give us the different varieties of Klein Ring.
The opposite side at the back turns in the opposite manner to this...
Hmm, how to draw that? That should finally give me a successful looking result if I can incorporate these...

Now I also understand the distinction with your explanation of the turning process Teragon to what I am demonstrating.
It appears that we are both correct for the results intended though your understanding of the path itself was better developed.
Mine is important because I need to work out the different orientation between the various versions of the Klein Ring and although it looks like turning it is just the distinction between varieties.
Originally I showed a need for dual turning to pave the path but that is not so; the dual turning is only necessary to create the distinct varieties.

Here is the correct ways the left back cross-section of the ring (or right if twisted the other way) should appear to us for each of the varieties (and not the last depiction):

You can consider that you are looking at it from the left (or right if you choose) with the full circles being the back cut of the 0° & 180° varieties and the lines being the 90° and 270° varieties...
You can also consider that the if the 0° cut at the back is on the left then the 180°cut will be, at the same time, on the right at the back though as looking from the right. ie.:

Now, next to work out if I can draw this on my Klein Ring varieties canvas...

Here they are showing the connections:

The left version shows it at 0° and the right shows it at 90°.

[gonegahgah]

I realise, looking at this again, that there is definitely one error to correct so far...
I'll try changing the equations tomorrow to:
x(u,v,s,t) = (R + r * cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * -sin(v/2) + cos(u + t) * cos(v / 2))) * sin(v * cos(s * cos(t)))
y(u,v,s,t) = (R + r *cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * -sin(v/2) + cos(u + t) * cos(v / 2))) * cos(v * cos(s * cos(t)))
z(u,v,s,t) = r * cos(s) * (sin(v / 2) * sin(u + t) * cos(t) * cos(v/2) + cos(u + t) * sin(v / 2))

What is "s" there?

The 's' is for sideways movement. Though the equations are wrong.

In case it helps, these should be the parametric equations for the whole objects:
90°-Moebius-spheritorus:
x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(u/2)*cos(v)
w = t*sin(u/2)*cos(v)
u, v = [0, 2pi]
w = [0, r]

I'm guessing the last 'w' on the previous line you mean 't' and that it goes from 0 to r?
I can see that the 'u' is how far around the ring we are and that 'v' is used to step each cross-section.
I'm reading these as primarily leaving 'x' and 'y' alone while moving the one path axis from 'w' around to 'z'; along the ring by the opposite 180° point.
Which is cool. I'm not to sure about the 't' and what purpose it serves?
It's current effect would seem to be to just increase the size of the shape over time?
Using 'r' directly would be enough wouldn't it for what you are describing?
So would the following suffice?
x = (r*sin(v) + R) * sin(u)
y = (r*sin(v) + R) * cos(u)
z = (r*cos(v)) * cos(u/2)
w = (r*cos(v)) * sin(u/2)
u, v = [0, 2π]

I came back to your equations because I realised something and I thought you might have already answered it for me.
Maybe you have somewhere else?
It occurs to me that your 90° version might not be the only variety of 90° variety that a 4Der would produce.
I feel my equations are suspect and need to be rewritten but it seems that the bi-rotational variety I described may still be a valid and unique form of a 90° variety.
A 4Der wouldn't really see them as different but we would. [Edit: or would that be vice-versa or both would see; still to be determined].

It's like the following rings:

We wouldn't really notice any difference except when they are side by side.
Of course, if we were in 4D these would just be the same ring.

However, there are a whole 180° of directions the twist could go through in 4D and those would be unique to each other.
I was thinking about the Moebius Strip and how it has only two directions of twist that are unique to us.
But, if we were in 4D it could have instead 180° of directions of twist that would all be unique.
Only 0° would appear to be a Moebius strip to us but the 4Der would see all of them as Moebius strips.

I'll have to rework my equations to more fit with this new reality.
Well, I'll actually have to fix them first to more accurately reflect the old reality first and then rework them.

[Teragon]

In case it helps, these should be the parametric equations for the whole objects:
90°-Moebius-spheritorus:
x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(u/2)*cos(v)
w = t*sin(u/2)*cos(v)
u, v = [0, 2pi]
w = [0, r]

I'm guessing the last 'w' on the previous line you mean 't' and that it goes from 0 to r?
I can see that the 'u' is how far around the ring we are and that 'v' is used to step each cross-section.
I'm reading these as primarily leaving 'x' and 'y' alone while moving the one path axis from 'w' around to 'z'; along the ring by the opposite 180° point.
Which is cool. I'm not to sure about the 't' and what purpose it serves?
It's current effect would seem to be to just increase the size of the shape over time?
Using 'r' directly would be enough wouldn't it for what you are describing?
So would the following suffice?

x, y, z and w are the four coordinates of space.
'u' is, as you recognized, how far around the ring.
As the surface of the Moebius strip is 3D, we need three variables to parameterize it:
'v' is how far around the circular cross-section. It's analogous to the small loop of a torus in 3D, which is added to the big loop, with the difference that it's oscillating between the z- and the w-direction with sin(u/2). 'u' and 'v' constitute the edge of the Moebius strip.
't' is not time, but the radial coordinate of the small loop. It just filles the area inside of the edge varying the radius of the circle that v traces out. It corresponds to the height of the Moebius band in 3D.

For the animations I've set 't' to a constant value, as they are only showing the outside of the image of the Moebius torus. The same is possible for most of the cross-sections, but not all of them. We have to imagine that the image doesn't have any holes though and we are seeing all of it at once from the forth dimension.

I came back to your equations because I realised something and I thought you might have already answered it for me.
Maybe you have somewhere else?
It occurs to me that your 90° version might not be the only variety of 90° variety that a 4Der would produce.
I feel my equations are suspect and need to be rewritten but it seems that the bi-rotational variety I described may still be a valid and unique form of a 90° variety.
A 4Der wouldn't really see them as different but we would. [Edit: or would that be vice-versa or both would see; still to be determined].

However, there are a whole 180° of directions the twist could go through in 4D and those would be unique to each other.
I was thinking about the Moebius Strip and how it has only two directions of twist that are unique to us.
But, if we were in 4D it could have instead 180° of directions of twist that would all be unique.
Only 0° would appear to be a Moebius strip to us but the 4Der would see all of them as Moebius strips.

I've realized that you are right about that. I made a stupid mistake in my contemplation about that. You can see it also in the equations, as after flipping the sign in front of 'u/2', which corresponds to the sense of the twist, only the sine-part changes and you can't transform the object back into it's original form by applying 180°-rotations, which are done by pairwise sign changes of the two coordinates involved.

Now I see that you can clearly see the chiraly in this animation, which shows a rotation in the zw-plane. The invariant plane is the xy-plane but it looks the same as a rotation in the xy-plane.



This is very deep. Under the same rotation, the other 90°-variety would appear to rotate in the other direction. If we rotate it in zw, as we're doing, or in xy, we would't be able to reverse the relative sense of the rotations to get to the other variety. If we rotate in xz, xw, yz or yw by 180°, one coordinate of both rotational planes would be involved and both rotations would revert their sense of rotation! So the relative sign of the rotations is always the same and both objects are really different.

A more general set of equations for the 90°-variety would be

x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(n*u/2)*cos(v)
w = t*sin(n*u/2)*cos(v)

where n is an arbitrary uneven whole number describing the number of twists a the chirality ... -5, -3, -1, 1, 3, 5, ...
An even n would correspond to twisted band that is not a Moebius band. n being a fraction of whole numbers would give... well, you can try it out for yourself.

My observation is that only for n = +-1 there is a symmetry under Clifford rotations (both rotations have the same period). In general, the rotation in the zw-plane has to be n times faster than the rotation in the xy-plane to keep the object invariant. Therefore combinated infinitesimal rotational symmtries need an additional number to be specified, describing the ratio of the periods of the rotations, which can involve fractions of whole numbers only. It's crazy how many new symmetries emerge with the 4D, compared to the step from 2D to 3D, where apart from the increased dimensionality you only get a rotoreflection, which is the same as a rotation in complexity.

[quickfur]

[...]
It's crazy how many new symmetries emerge with the 4D, compared to the step from 2D to 3D, where apart from the increased dimensionality you only get a rotoreflection, which is the same as a rotation in complexity.

Actually, going from 2D to 3D introduces a whole new concept of rotation: orientation. In 2D, all rotations are isomorphic up to translation, and there is only one unique plane of rotation (albeit many possible centers of rotation), i.e., the 2D plane itself. Stepping up to 3D, however, greatly complicates this picture by the possibility of rotations differing in orientation, and no longer being confined to a unique plane. This isn't just a superficial difference either; the 3D rotation group, S3, is qualitatively more complex than the 2D rotation group, S2, such that S3 admits paradoxical decompositions whereas S2 doesn't. So S3 gives rise to the possibilty of the Banach-Tarski paradox, whereas the same is impossible with S2.

Of course, the 4D rotation group is an even bigger step up, in that it admits Clifford double rotations, a strange kind of rotation that has an infinite number of stationary planes, and which corresponds with the Hopf fibration. It is also unique in that 4D is the only dimension in which the Clifford double rotation is orientable, whereas all higher dimensions, which include S4 as a subgroup, no longer have this property.

[Teragon]

That is true, quickfur, but what I mean is, the number of possible types of symmetry elements hardly increases.

Of course, the 4D rotation group is an even bigger step up, in that it admits Clifford double rotations, a strange kind of rotation that has an infinite number of stationary planes, and which corresponds with the Hopf fibration. It is also unique in that 4D is the only dimension in which the Clifford double rotation is orientable, whereas all higher dimensions, which include S4 as a subgroup, no longer have this property.

How is this? I can't imagine how to obtain the same rotation with a different orientation of the defining elements. What about triple rotations?
Do you mean the defining planes by "stationay planes"? I mean there is no plane that remains stationary in a Clifford rotation in 4D. If I got it right the space of orientations of a Clifford rotation has the same topology as the space of orientations of rotations in 3D.

[quickfur]

Ah, sorry, I confused myself. There are no stationary planes in a clifford rotation, only a stationary point. But there are an infinite number of rotational planes; i.e., an infinite number of planes in which the clifford rotation traces out circles.

As for the existence of orientation, it's not immediately obvious to see with a duocylinder. But it's pretty obvious if you consider the Hopf fiber bundle, or any discrete analogue thereof, such as the rings of the bi-24-diminished 600-cell or the swirl-diminished rectified 600-cell. Basically, the fibers in the Hopf fibration wind around each other, and as such exhibits either lefthandedness or righthandedness. This orientation always exists in the 4D subspace in which the clifford rotation takes place, but in 5D and above, one orientation can be converted to the other simply by rotating through the space outside of the 4D subspace, so they are indistinct. In 4D, however, they remain distinct. So the Hopf fibration has two distinct orientations related via a mirror-image operation.

Here's a projection of the swirldiminished rectified 600-cell that shows some of the rings of cells that correspond with a subset of the Hopf fibration:



Sorry, the image is a bit cluttered, but if you know how to do cross-eyed 3D viewing, they are stereoscopic pairs, and you'll be able to see more clearly the white column in the middle. That's half of a toroidal ring of cells that wrap around the polytope; it projects to a vertical column because it lies in the YW plane and we're projecting along the W axis. Around it you can see orange, green, and blue rings of cells that wrap around it: these are other toroidal rings of cells. They are actually isomorphic to the white column (and to each other) under a symmetry operation; and there are 5 of them here. Then around these 5 rings are another 5 rings, angled closer to the horizontal, two of which are clearly visible here in light yellow and magenta. There are also 5 of these (it's kinda hard to see all of them clearly, though 3 can be discerned with some effort). Lastly, but not shown here because of clutter, is a horizontal ring forming an equator around the whole thing. This horizontal ring, corresponding to the orthogonal ring of a duocylinder with one ring parallel to the white column (ring), is the 12th ring of cells around the polytope. Note that all 12 rings are isomorphic to each other under the polytope's symmetry group. Therefore, they correspond with a 12-fiber subset of the Hopf fibration.

Now note that each layer of rings wrap around each other in an oriented way; the mirror image of the above image represents a distinct polytope that has the same structure but of a different handedness. So there are L- and R- variants of the swirldiminished rectified 600-cell, somewhat analogous to L- and R- variants of the snub dodecahedron (but it's not a complete analogy, as the underlying geometry is different).

Furthermore, each of the 12 rings defines a 2D plane in which circles will be traced by a clifford rotation. So there are at least 12 rotational planes corresponding with the same clifford rotation. That implies that given a clifford rotation, there is no unique decomposition into a pair of orthogonal rotations! You can pick any of 6 possible pairs of orthogonal planes, and they will equally define a valid pair of rotations that comprises the same clifford rotation. But we aren't restricted to 12 rotational planes, because the above polytope also features 20 rings of square pyramid cells, which are also great circles equivalent to each other under the symmetry group. So actually, there are 32 rotational planes here. Well, in fact, this is just a subset of the Hopf fibration; there are an infinite number of orthogonal fiber pairs in the Hopf fibration, and all of them are valid decompositions of the same clifford rotation into two plane rotations. So in this sense, the clifford rotation is unusual: in a general double rotation where the rates of rotation of the respective plane rotations are not equal, there is generally only a single pair of plane rotations that comprise that double rotation. But the clifford rotation has an infinite number of possible decompositions. In this sense, the clifford rotation loses one degree of orientation, yet it still retains left- and right-handedness.

[Teragon]

As for the existence of orientation, it's not immediately obvious to see with a duocylinder. But it's pretty obvious if you consider the Hopf fiber bundle, or any discrete analogue thereof, such as the rings of the bi-24-diminished 600-cell or the swirl-diminished rectified 600-cell. Basically, the fibers in the Hopf fibration wind around each other, and as such exhibits either lefthandedness or righthandedness. This orientation always exists in the 4D subspace in which the clifford rotation takes place, but in 5D and above, one orientation can be converted to the other simply by rotating through the space outside of the 4D subspace, so they are indistinct. In 4D, however, they remain distinct. So the Hopf fibration has two distinct orientations related via a mirror-image operation.

The Clifford rotation is achiral in 5D, that's clear. But according to this line of argument rotations in 3D would also be non-orientable. When you flip a double rotation in order to get what would be the other cirality in 4D, the configuration of the rotation has also changed (one part of the rotation is going the other way round). I may be wrong, but as I got it, something is non-orientable, if the element that defines it (in this case maby a tensor?) is unambiguous. Put differently at the same place in the configuration space of the rotation, there is no ambiguos tensor (or whatever) to describe it. This is not the case for such a flip though, because both configurations are different.

This is a very hard stereoscopic pair for me. Just can't really focus and recognize the shapes of the polyhedra.

Here's a projection of the swirldiminished rectified 600-cell that shows some of the rings of cells that correspond with a subset of the Hopf fibration:

As if a 120-cell was not enough for this purpose

Furthermore, each of the 12 rings defines a 2D plane in which circles will be traced by a clifford rotation. So there are at least 12 rotational planes corresponding with the same clifford rotation. That implies that given a clifford rotation, there is no unique decomposition into a pair of orthogonal rotations! You can pick any of 6 possible pairs of orthogonal planes, and they will equally define a valid pair of rotations that comprises the same clifford rotation. But we aren't restricted to 12 rotational planes, because the above polytope also features 20 rings of square pyramid cells, which are also great circles equivalent to each other under the symmetry group. So actually, there are 32 rotational planes here. Well, in fact, this is just a subset of the Hopf fibration; there are an infinite number of orthogonal fiber pairs in the Hopf fibration, and all of them are valid decompositions of the same clifford rotation into two plane rotations. So in this sense, the clifford rotation is unusual: in a general double rotation where the rates of rotation of the respective plane rotations are not equal, there is generally only a single pair of plane rotations that comprise that double rotation. But the clifford rotation has an infinite number of possible decompositions. In this sense, the clifford rotation loses one degree of orientation, yet it still retains left- and right-handedness.

I agree. But now I'm confused why it is still orientable in 4D.

Do you agree that yet there is an infinate number of different configurations for double rotations around a fixed center, i.e. that the configuration space of a double rotation is a sphere?

[wendy]

Parity of rotation applies in every dimension. The trick here is to note that a ring (ie the surface of an n-2 sphere), can be given a vector sense that is orthogonal to the plane it is in, and in even dimensions, clifford-rotation gives the sphere such a sense, and passing through it is with or against the vector, or left / right rotation.

[Klitzing]

This is a very hard stereoscopic pair for me. Just can't really focus and recognize the shapes of the polyhedra.

Here's a projection of the swirldiminished rectified 600-cell that shows some of the rings of cells that correspond with a subset of the Hopf fibration:

As if a 120-cell was not enough for this purpose

Well, you are right, the swirl symmetry is digged within the 600-cell already, but because of the full tetrahedral symmetry of its cells it is not so "obvious" there. For that purpose "spidrox" (the 'swirlprismatically diminished rectified hexacosachoron') was chosen by Quickfur.

A further such figure would be the exeptional uniform polychoron, by Norman Johnson simply called "gap" (for 'grand antiprism'), cf. on wikipedia resp. on Quickfur's own website, which would have served too and indeed is nothing but a bicyclical deca-diminishing of the hexacosachoron. Even so, gap does not display all 12 fibres, instead it just uses the 2 antipodal ones for the centers of the girdles of 10 pentagonal antiprisms each, cf. that "bicyclical" part. The remainder there is still filled by un-touched tetrahedra of the 600-cell. (Those then do not allow for further such pentagonal antiprismal diminishings.)

But there indeed is also an other cut out from that 600-cell, which fully displays the full swirlprism symmetry. That one is "spysp" (acronym for 'small pyramidic swirlprism'), which is an current subject of discussion in an other thread, e.g. cf. here. That one uses just a single cell type (pentagonal pyramids, a.k.a. J1), and also has just a single vertex figure, which could be obtained from the "normal" pentagonal antiprism, when its descending lacing edges would be erased and give way for an underlying orthogonal edge, which then is longer by the golden ratio. (A display of that vertex figure could be found on Hedrondude's website at the page on swirlprismatic scaliforms.) - Because of having both, a single cell type and a single vertex type, this figure then is not only scaliform, it even is a noble polychoron.

--- rk

[Klitzing]

(Those then do not allow for further such pentagonal antiprismal diminishings.)

This is kind of wrong, for sure. It clearly can. That one then would be sisp, the 'small swirlprism' (cf. on Jonathan's website here). It just would be a self-intersecting non-convex polychoron, so. And just like spysp it would be a noble figure, this time with 120 equivalent vertices and 120 equivalent pentagonal antiprismatic cells.

Spysp OTOH had a count of 120 equivalent vertices and 240 equivalent pentagonal pyramidic cells. Moreover it would be non-convex too, but it still is non-self-intersecting! (Thus, most probably, better suited for visualization, I guess.)

--- rk

[Teragon]

There are another two cool objects with the same topology as the Moebius spheritorus. One of them is the Moebius cyltorus.

Moebius cyltorus (Moebius cubinder)
Full name: x° n-Moebius cyltorus
Order: 1
Level: 1
Family: Moebius 3-spheritorus
Cut of a cyltorus, twisted ½+n times
Cross section: Cylinder section
Open directions: 2
Closed directions: 1
Twisted directions: 1
Surface dimensionality: 3
Chiral (90°) / achiral (0°)

The surface of this objects has the same width at any point. For the 90°-variety it's direction rotates from w to z while moving around the object keeping a rectangular cross section. It's an object that can have a big length, but as you go around the loop the long side changes from w to z and back. I wonder how it rolls.

For the 0°-variety the width is constant in w direction and changes in z-direction (if the height is bigger than the loop diameter) with its cross section changing between circular and rectangular.

Finally some perspective projections (blue = far, red = close) of the 90° variety. Its "height" (=cylinder diameter) is identical to its outer loop diameter.

Rotation in zw. You see the same symmetry under double rotations as for the 90° Moebius-spheritorus.


Rotation in yw:


For the following pictures, the width of the Moebius strip inside the loop plane has been set to a smaller value, because that makes it easier to see what's going on. You see the loop nearly undistorted, while the longe edge is twisting around from z to w. As the short edge (the area facing the top and the bottom) lies inside the plane of the loop, it has always the same width all around the loop, while its distance changes as it is offset by the long distance rotating in wz.





(Sorry for the imperfections in the visual appearance.)

In the last three images you can see the strip with your line of sight inside the plane of the loop, so that the center of the loop looks like clearly defined straight line, where the object crosses itself. Actually the object never crosses itself - as the different colors suggest, one part is closer in w than another. Starting from the center along the straight line, both parts of the loop approach each other in w, until they connect at the two end points. These points are also the only points, where the rectangular cross section of the object is undistorted.
You see the directions were the Moebius strip is extended nearly undistorted as they extent in the plane perpendicular to the loop. The long egde of the rectangular cross section coiles around always keeping its distance to the center, tracing out a circle that is modulated by an offset perpendicular to it that goes with the sine of where you are on the loop.

[gonegahgah]

Code: Select all

x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(n*u/2)*cos(v)
w = t*sin(n*u/2)*cos(v)

I was looking at your formulas Teragon (if you're still around?).
I'm a little concerned that the {x}^{y} (side and back) don’t really seem to give up anything to the w (4D) which I thought they would (especially at the highest point) if the path is tumbling.
The varieties in your depiction all seem to be identical; if just from a different forward view?

If you are here(?) is it possible to try out the following parametric equations?

Code: Select all

x = R * sin(u) + r * ( sin(v) * sin(u) )
y = R * cos(u) + r * ( cos(v) * cos(u/2) * cos(t) – sin(v) * cos(u) * sin(t) )
z = r * ( cos(v) * sin(u/2) )
w = r * ( cos(v) * cos(u/2) * sin(t) + sin(v) * cos(u) * cos(t) )

R - major radius, r - path radius, t - Klein Strip variety (-π to π), u - Steps R, v - Steps r.

I'm not sure they are the maximum ideal yet but they maintain a circular path whilst tumbling uniquely and evenly to each other.
To be ideal I'm guessing probably all values should be somehow effected by t (as yours are and which mine aren't).
Here's hoping!

[Teragon]

Code: Select all

x = sin(u)*(R + t*sin(v))
y = cos(u)*(R + t*sin(v))
z = t*cos(n*u/2)*cos(v)
w = t*sin(n*u/2)*cos(v)

I'm a little concerned that the {x}^{y} (side and back) don’t really seem to give up anything to the w (4D) which I thought they would (especially at the highest point) if the path is tumbling.
The varieties in your depiction all seem to be identical; if just from a different forward view?

Hello, the equation you quoted is not supposed to show varieties with different twist planes. It's all the 90°-variety and 'n' just parametrizes the number of twists in the twist plane (is that what you mean?). The parameter 'u' describes the revolution around the loop in the xy plane and at the same time, the rotation of the band in zw.

If you are here(?) is it possible to try out the following parametric equations?

Don't have my program at hand right now, but I'll try soon.

[gonegahgah]

Thanks Teragon.

[Teragon]

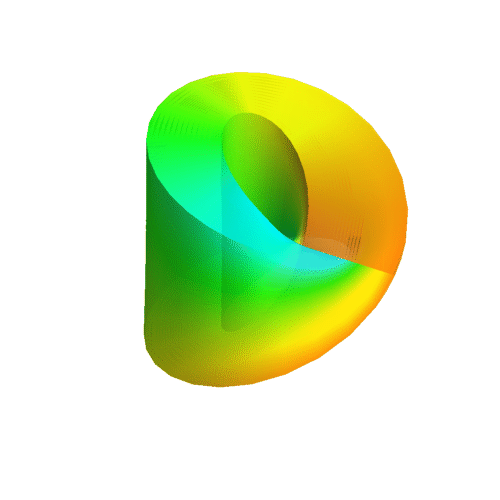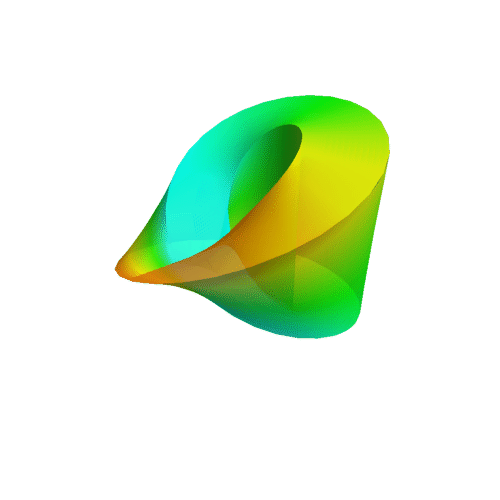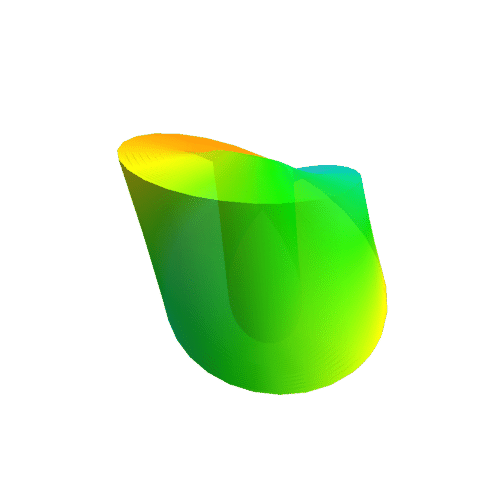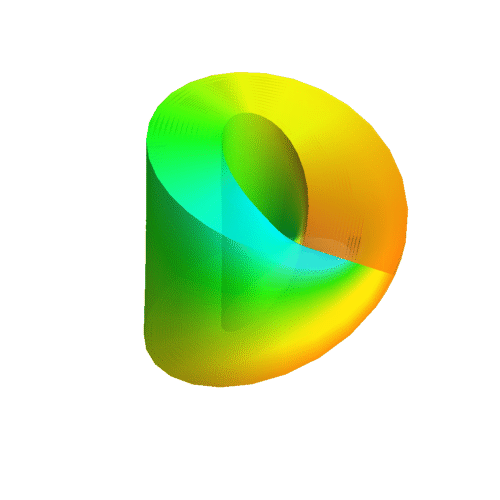
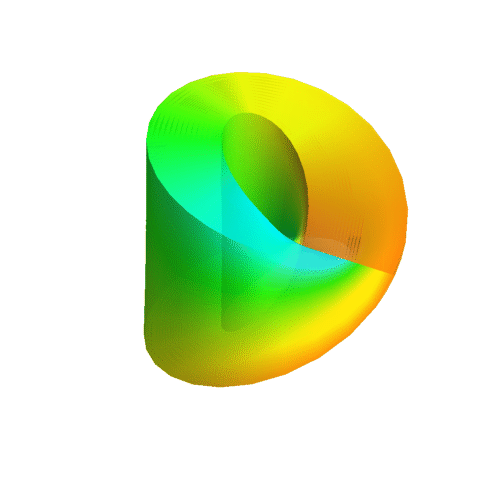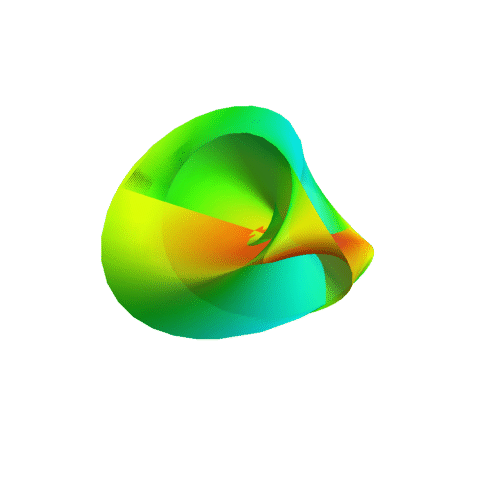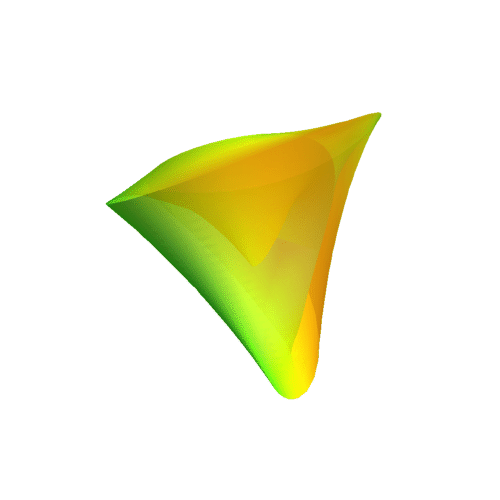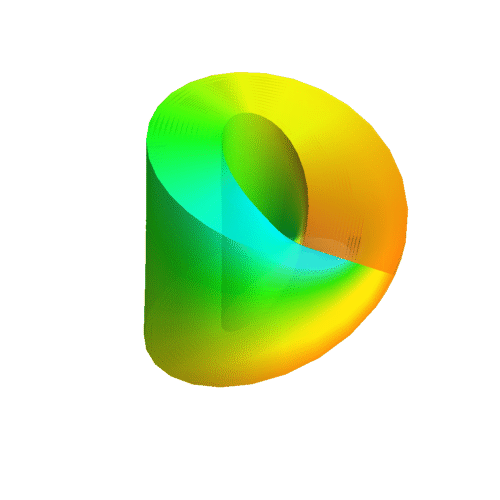
Do you know this when you get back to code you wrote after ages and nothing is working any more? Couldn't find what caused the error, so I can't plot it at the moment. I also can't figure out the logics of your equations. The u- and v-direction are obviously not perpendicular to each other, which is inelegant at best. What I'd come up with would be the following:

The 90° variety of the Moebius spheritorus we know is given by:

Code: Select all

x = sin(u)*(R + r*sin(v))
y = cos(u)*(R + r*sin(v))
z = r*sin(n*u/2)*cos(v)
w = r*cos(n*u/2)*cos(v)


To remind ourselves again, the constants here are R and n. R is the radius of the loop, n is an odd number and is related to the number of twists ( = abs(n)/2)). u describes a revolution around the big loop, which lies in the xy plane. v describes the revolution around the small loop, which lies in the radial direction of the big loop (x/y) and z/w. The twist thus happens in the zw plane and the orthogonal vector of the strip always points in some direction within this plane. As this is always 90° to the plane of the big loop, I called this the 90° variety of the Moebius spheritorus. r is a parameter too and fills out the plane of the small loop.

We should be able to write the 0° variety like this:

Code: Select all

x = sin(u)*(R + r*sin(v)*sin(n*u/2))
y = cos(u)*(R + r*sin(v)*sin(n*u/2))
z = r*cos(n*u/2)*sin(v)
w = r*cos(v)

One direction of the small loop is now always w and the trade-off happens between z and the radial coordinate of the big loop (x/y). Thus the orthogonal vector of the strips 3-surface rotates between w and xy, between 0° and 90° to the plane of the strip. Actually the 0° variety is much easier to imagine than the 90° one. It's just a usual Moebius strip in 3D extruded to a circle in the w dimension. Extruded objects are always achiral due to the preserved mirror symmetry.

Between those two extremes, there is a continuum of possibilities. The minimum angle of the orthogonal vector to the plane of the strip can assume any value between 0 and 90°. Intuitively, I'd say, those possibilities can be described by weighting the 90°- and 0°-variety with the sin and cos of the twist parameter t, respectively. The result would look like this:

Code: Select all

x = sin(u) * (R + r*sin(v) * (sin(t) + sin(n*u/2)*cos(t))
y = cos(u) * (R + r*sin(v) * (sin(t) + sin(n*u/2)*cos(t)))
z = r * (sin(n*u/2)*cos(v)*sin(t) + cos(n*u/2)*sin(v)*cos(t))
w = r*cos(v) * (cos(n*u/2)*sin(t) + cos(t))


It's interesting to see how chirality is built into the strip. t can adapt values between -pi/2 and +pi/2 and flipping the sign means changing the chirality. For t = 0, flipping the sign doesn't do anything, because the strip becomes achiral at this point. So the mirror image of the strip is the same as a rotated version of the strip.

It should be noted that changing the sign of n must have the same effect on the geometry of the object as changing the sign of t.

Edit: Code corrected

[gonegahgah]

Do you know this when you get back to code you wrote after ages and nothing is working any more? Couldn't find what caused the error, so I can't plot it at the moment.

I know that feeling far too much. I'm trying to get to the point where I keep track of working versions better. Maybe one day hopefully!
It is sad as well as I was looking forward to seeing how it looked in your code...

Thank you for your new formulations Teragon. I was very interested to find out if they worked nicely.
I am trying to achieve results where the formulations spit out circles along the length of the Klein Strip.
In order to achieve that all the points need to be a distance of r from the centre.

I did up a spreadsheet to quickly test your new formulations.
To test this I set the R=0 and n=1 for your equations. I also set r=1 just to get unit circles.
Here are a subset of results:

Code: Select all

t=-3.14                                                         | t=0                           
u       v       t       w       x       y       z       r"      | u       v       t       w       x       y       z       r"
-3.14   -3.14   -3.14   -1.00   0.00    0.00    1.00    1.41    | -3.14   -3.14   0.00    1.00    0.00    0.00    1.00    1.41
-3.14   -2.62   -3.14   -1.00   0.00    0.50    0.87    1.41    | -3.14   -2.62   0.00    1.00    0.00    -0.50   0.87    1.41
-3.14   -2.09   -3.14   -1.00   0.00    0.87    0.50    1.41    | -3.14   -2.09   0.00    1.00    0.00    -0.87   0.50    1.41
-3.14   -1.57   -3.14   -1.00   0.00    1.00    0.00    1.41    | -3.14   -1.57   0.00    1.00    0.00    -1.00   0.00    1.41
-3.14   -1.05   -3.14   -1.00   0.00    0.87    -0.50   1.41    | -3.14   -1.05   0.00    1.00    0.00    -0.87   -0.50   1.41
-3.14   -0.52   -3.14   -1.00   0.00    0.50    -0.87   1.41    | -3.14   -0.52   0.00    1.00    0.00    -0.50   -0.87   1.41
-3.14   0.00    -3.14   -1.00   0.00    0.00    -1.00   1.41    | -3.14   0.00    0.00    1.00    0.00    0.00    -1.00   1.41
-3.14   0.52    -3.14   -1.00   0.00    -0.50   -0.87   1.41    | -3.14   0.52    0.00    1.00    0.00    0.50    -0.87   1.41
-3.14   1.05    -3.14   -1.00   0.00    -0.87   -0.50   1.41    | -3.14   1.05    0.00    1.00    0.00    0.87    -0.50   1.41
-3.14   1.57    -3.14   -1.00   0.00    -1.00   0.00    1.41    | -3.14   1.57    0.00    1.00    0.00    1.00    0.00    1.41
-3.14   2.09    -3.14   -1.00   0.00    -0.87   0.50    1.41    | -3.14   2.09    0.00    1.00    0.00    0.87    0.50    1.41
-3.14   2.62    -3.14   -1.00   0.00    -0.50   0.87    1.41    | -3.14   2.62    0.00    1.00    0.00    0.50    0.87    1.41
-3.14   3.14    -3.14   -1.00   0.00    0.00    1.00    1.41    | -3.14   3.14    0.00    1.00    0.00    0.00    1.00    1.41
------------------------------------------------------------------------------------------------------------------------------
0.00    -3.14   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -3.14   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -2.62   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -2.62   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -2.09   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -2.09   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -1.57   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -1.57   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -1.05   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -1.05   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -0.52   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -0.52   0.00    1.00    0.00    0.00    0.00    1.00
0.00    0.00    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    0.00    0.00    1.00    0.00    0.00    0.00    1.00
0.00    0.52    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    0.52    0.00    1.00    0.00    0.00    0.00    1.00
0.00    1.05    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    1.05    0.00    1.00    0.00    0.00    0.00    1.00
0.00    1.57    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    1.57    0.00    1.00    0.00    0.00    0.00    1.00
0.00    2.09    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    2.09    0.00    1.00    0.00    0.00    0.00    1.00
0.00    2.62    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    2.62    0.00    1.00    0.00    0.00    0.00    1.00
0.00    3.14    -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    3.14    0.00    1.00    0.00    0.00    0.00    1.00

Some of the resultant co-ordinates are not equal to r"=1 from their centre?

I get this resultant r" by calculating:

Code: Select all

r" = √( w² + x² + y² + z²)

That's not to say that your formulations could not still result in producing circles overall (but there are some resultant r" in the fuller spreadsheet that are <1 so this is probably not likely).
It's also not to say that these aren't a type of Klein Strips.
It's just to say that it is not spitting out circles like I'm trying to achieve.
I can provide a longer subsection of data results of your equations if you would like?

The formulations I have developed so far (and haven't been able to get past yet) produce the following results for the same (plus further) subset:

Code: Select all

t=-3.14                                                         | t=0                                                         
u       v       t       w       x       y       z       r"      | u       v       t       w       x       y       z       r" 
-3.14   -3.14   -3.14   0.00    0.00    0.00    -1.00   1.00    | -3.14   -3.14   0.00    0.00    0.00    0.00    -1.00   1.00
-3.14   -2.62   -3.14   0.50    0.00    0.00    -0.87   1.00    | -3.14   -2.62   0.00    -0.50   0.00    0.00    -0.87   1.00
-3.14   -2.09   -3.14   0.87    0.00    0.00    -0.50   1.00    | -3.14   -2.09   0.00    -0.87   0.00    0.00    -0.50   1.00
-3.14   -1.57   -3.14   1.00    0.00    0.00    0.00    1.00    | -3.14   -1.57   0.00    -1.00   0.00    0.00    0.00    1.00
-3.14   -1.05   -3.14   0.87    0.00    0.00    0.50    1.00    | -3.14   -1.05   0.00    -0.87   0.00    0.00    0.50    1.00
-3.14   -0.52   -3.14   0.50    0.00    0.00    0.87    1.00    | -3.14   -0.52   0.00    -0.50   0.00    0.00    0.87    1.00
-3.14   0.00    -3.14   0.00    0.00    0.00    1.00    1.00    | -3.14   0.00    0.00    0.00    0.00    0.00    1.00    1.00
-3.14   0.52    -3.14   -0.50   0.00    0.00    0.87    1.00    | -3.14   0.52    0.00    0.50    0.00    0.00    0.87    1.00
-3.14   1.05    -3.14   -0.87   0.00    0.00    0.50    1.00    | -3.14   1.05    0.00    0.87    0.00    0.00    0.50    1.00
-3.14   1.57    -3.14   -1.00   0.00    0.00    0.00    1.00    | -3.14   1.57    0.00    1.00    0.00    0.00    0.00    1.00
-3.14   2.09    -3.14   -0.87   0.00    0.00    -0.50   1.00    | -3.14   2.09    0.00    0.87    0.00    0.00    -0.50   1.00
-3.14   2.62    -3.14   -0.50   0.00    0.00    -0.87   1.00    | -3.14   2.62    0.00    0.50    0.00    0.00    -0.87   1.00
-3.14   3.14    -3.14   0.00    0.00    0.00    -1.00   1.00    | -3.14   3.14    0.00    0.00    0.00    0.00    -1.00   1.00
----------------------------------------------------------------|-------------------------------------------------------------
0.00    -3.14   -3.14   0.00    0.00    1.00    0.00    1.00    | 0.00    -3.14   0.00    0.00    0.00    -1.00   0.00    1.00
0.00    -2.62   -3.14   -0.50   0.00    0.87    0.00    1.00    | 0.00    -2.62   0.00    0.50    0.00    -0.87   0.00    1.00
0.00    -2.09   -3.14   -0.87   0.00    0.50    0.00    1.00    | 0.00    -2.09   0.00    0.87    0.00    -0.50   0.00    1.00
0.00    -1.57   -3.14   -1.00   0.00    0.00    0.00    1.00    | 0.00    -1.57   0.00    1.00    0.00    0.00    0.00    1.00
0.00    -1.05   -3.14   -0.87   0.00    -0.50   0.00    1.00    | 0.00    -1.05   0.00    0.87    0.00    0.50    0.00    1.00
0.00    -0.52   -3.14   -0.50   0.00    -0.87   0.00    1.00    | 0.00    -0.52   0.00    0.50    0.00    0.87    0.00    1.00
0.00    0.00    -3.14   0.00    0.00    -1.00   0.00    1.00    | 0.00    0.00    0.00    0.00    0.00    1.00    0.00    1.00
0.00    0.52    -3.14   0.50    0.00    -0.87   0.00    1.00    | 0.00    0.52    0.00    -0.50   0.00    0.87    0.00    1.00
0.00    1.05    -3.14   0.87    0.00    -0.50   0.00    1.00    | 0.00    1.05    0.00    -0.87   0.00    0.50    0.00    1.00
0.00    1.57    -3.14   1.00    0.00    0.00    0.00    1.00    | 0.00    1.57    0.00    -1.00   0.00    0.00    0.00    1.00
0.00    2.09    -3.14   0.87    0.00    0.50    0.00    1.00    | 0.00    2.09    0.00    -0.87   0.00    -0.50   0.00    1.00
0.00    2.62    -3.14   0.50    0.00    0.87    0.00    1.00    | 0.00    2.62    0.00    -0.50   0.00    -0.87   0.00    1.00
0.00    3.14    -3.14   0.00    0.00    1.00    0.00    1.00    | 0.00    3.14    0.00    0.00    0.00    -1.00   0.00    1.00
----------------------------------------------------------------|-------------------------------------------------------------
0.52    -3.14   -3.14   0.00    0.00    0.97    0.26    1.00    | 0.52    -3.14   0.00    0.00    0.00    -0.97   0.26    1.00
0.52    -2.62   -3.14   -0.43   -0.25   0.84    0.22    1.00    | 0.52    -2.62   0.00    0.43    -0.25   -0.84   0.22    1.00
0.52    -2.09   -3.14   -0.75   -0.43   0.48    0.13    1.00    | 0.52    -2.09   0.00    0.75    -0.43   -0.48   0.13    1.00
0.52    -1.57   -3.14   -0.87   -0.50   0.00    0.00    1.00    | 0.52    -1.57   0.00    0.87    -0.50   0.00    0.00    1.00
0.52    -1.05   -3.14   -0.75   -0.43   -0.48   -0.13   1.00    | 0.52    -1.05   0.00    0.75    -0.43   0.48    -0.13   1.00
0.52    -0.52   -3.14   -0.43   -0.25   -0.84   -0.22   1.00    | 0.52    -0.52   0.00    0.43    -0.25   0.84    -0.22   1.00
0.52    0.00    -3.14   0.00    0.00    -0.97   -0.26   1.00    | 0.52    0.00    0.00    0.00    0.00    0.97    -0.26   1.00
0.52    0.52    -3.14   0.43    0.25    -0.84   -0.22   1.00    | 0.52    0.52    0.00    -0.43   0.25    0.84    -0.22   1.00
0.52    1.05    -3.14   0.75    0.43    -0.48   -0.13   1.00    | 0.52    1.05    0.00    -0.75   0.43    0.48    -0.13   1.00
0.52    1.57    -3.14   0.87    0.50    0.00    0.00    1.00    | 0.52    1.57    0.00    -0.87   0.50    0.00    0.00    1.00
0.52    2.09    -3.14   0.75    0.43    0.48    0.13    1.00    | 0.52    2.09    0.00    -0.75   0.43    -0.48   0.13    1.00
0.52    2.62    -3.14   0.43    0.25    0.84    0.22    1.00    | 0.52    2.62    0.00    -0.43   0.25    -0.84   0.22    1.00
0.52    3.14    -3.14   0.00    0.00    0.97    0.26    1.00    | 0.52    3.14    0.00    0.00    0.00    -0.97   0.26    1.00
----------------------------------------------------------------|-------------------------------------------------------------
1.05    -3.14   -3.14   0.00    0.00    0.87    0.50    1.00    | 1.05    -3.14   0.00    0.00    0.00    -0.87   0.50    1.00
1.05    -2.62   -3.14   -0.25   -0.43   0.75    0.43    1.00    | 1.05    -2.62   0.00    0.25    -0.43   -0.75   0.43    1.00
1.05    -2.09   -3.14   -0.43   -0.75   0.43    0.25    1.00    | 1.05    -2.09   0.00    0.43    -0.75   -0.43   0.25    1.00
1.05    -1.57   -3.14   -0.50   -0.87   0.00    0.00    1.00    | 1.05    -1.57   0.00    0.50    -0.87   0.00    0.00    1.00
1.05    -1.05   -3.14   -0.43   -0.75   -0.43   -0.25   1.00    | 1.05    -1.05   0.00    0.43    -0.75   0.43    -0.25   1.00
1.05    -0.52   -3.14   -0.25   -0.43   -0.75   -0.43   1.00    | 1.05    -0.52   0.00    0.25    -0.43   0.75    -0.43   1.00
1.05    0.00    -3.14   0.00    0.00    -0.87   -0.50   1.00    | 1.05    0.00    0.00    0.00    0.00    0.87    -0.50   1.00
1.05    0.52    -3.14   0.25    0.43    -0.75   -0.43   1.00    | 1.05    0.52    0.00    -0.25   0.43    0.75    -0.43   1.00
1.05    1.05    -3.14   0.43    0.75    -0.43   -0.25   1.00    | 1.05    1.05    0.00    -0.43   0.75    0.43    -0.25   1.00
1.05    1.57    -3.14   0.50    0.87    0.00    0.00    1.00    | 1.05    1.57    0.00    -0.50   0.87    0.00    0.00    1.00
1.05    2.09    -3.14   0.43    0.75    0.43    0.25    1.00    | 1.05    2.09    0.00    -0.43   0.75    -0.43   0.25    1.00
1.05    2.62    -3.14   0.25    0.43    0.75    0.43    1.00    | 1.05    2.62    0.00    -0.25   0.43    -0.75   0.43    1.00
1.05    3.14    -3.14   0.00    0.00    0.87    0.50    1.00    | 1.05    3.14    0.00    0.00    0.00    -0.87   0.50    1.00
----------------------------------------------------------------|-------------------------------------------------------------
1.57    -3.14   -3.14   0.00    0.00    0.71    0.71    1.00    | 1.57    -3.14   0.00    0.00    0.00    -0.71   0.71    1.00
1.57    -2.62   -3.14   0.00    -0.50   0.61    0.61    1.00    | 1.57    -2.62   0.00    0.00    -0.50   -0.61   0.61    1.00
1.57    -2.09   -3.14   0.00    -0.87   0.35    0.35    1.00    | 1.57    -2.09   0.00    0.00    -0.87   -0.35   0.35    1.00
1.57    -1.57   -3.14   0.00    -1.00   0.00    0.00    1.00    | 1.57    -1.57   0.00    0.00    -1.00   0.00    0.00    1.00
1.57    -1.05   -3.14   0.00    -0.87   -0.35   -0.35   1.00    | 1.57    -1.05   0.00    0.00    -0.87   0.35    -0.35   1.00
1.57    -0.52   -3.14   0.00    -0.50   -0.61   -0.61   1.00    | 1.57    -0.52   0.00    0.00    -0.50   0.61    -0.61   1.00
1.57    0.00    -3.14   0.00    0.00    -0.71   -0.71   1.00    | 1.57    0.00    0.00    0.00    0.00    0.71    -0.71   1.00
1.57    0.52    -3.14   0.00    0.50    -0.61   -0.61   1.00    | 1.57    0.52    0.00    0.00    0.50    0.61    -0.61   1.00
1.57    1.05    -3.14   0.00    0.87    -0.35   -0.35   1.00    | 1.57    1.05    0.00    0.00    0.87    0.35    -0.35   1.00
1.57    1.57    -3.14   0.00    1.00    0.00    0.00    1.00    | 1.57    1.57    0.00    0.00    1.00    0.00    0.00    1.00
1.57    2.09    -3.14   0.00    0.87    0.35    0.35    1.00    | 1.57    2.09    0.00    0.00    0.87    -0.35   0.35    1.00
1.57    2.62    -3.14   0.00    0.50    0.61    0.61    1.00    | 1.57    2.62    0.00    0.00    0.50    -0.61   0.61    1.00
1.57    3.14    -3.14   0.00    0.00    0.71    0.71    1.00    | 1.57    3.14    0.00    0.00    0.00    -0.71   0.71    1.00
----------------------------------------------------------------|-------------------------------------------------------------
2.09    -3.14   -3.14   0.00    0.00    0.50    0.87    1.00    | 2.09    -3.14   0.00    0.00    0.00    -0.50   0.87    1.00
2.09    -2.62   -3.14   0.25    -0.43   0.43    0.75    1.00    | 2.09    -2.62   0.00    -0.25   -0.43   -0.43   0.75    1.00
2.09    -2.09   -3.14   0.43    -0.75   0.25    0.43    1.00    | 2.09    -2.09   0.00    -0.43   -0.75   -0.25   0.43    1.00
2.09    -1.57   -3.14   0.50    -0.87   0.00    0.00    1.00    | 2.09    -1.57   0.00    -0.50   -0.87   0.00    0.00    1.00
2.09    -1.05   -3.14   0.43    -0.75   -0.25   -0.43   1.00    | 2.09    -1.05   0.00    -0.43   -0.75   0.25    -0.43   1.00
2.09    -0.52   -3.14   0.25    -0.43   -0.43   -0.75   1.00    | 2.09    -0.52   0.00    -0.25   -0.43   0.43    -0.75   1.00
2.09    0.00    -3.14   0.00    0.00    -0.50   -0.87   1.00    | 2.09    0.00    0.00    0.00    0.00    0.50    -0.87   1.00
2.09    0.52    -3.14   -0.25   0.43    -0.43   -0.75   1.00    | 2.09    0.52    0.00    0.25    0.43    0.43    -0.75   1.00
2.09    1.05    -3.14   -0.43   0.75    -0.25   -0.43   1.00    | 2.09    1.05    0.00    0.43    0.75    0.25    -0.43   1.00
2.09    1.57    -3.14   -0.50   0.87    0.00    0.00    1.00    | 2.09    1.57    0.00    0.50    0.87    0.00    0.00    1.00
2.09    2.09    -3.14   -0.43   0.75    0.25    0.43    1.00    | 2.09    2.09    0.00    0.43    0.75    -0.25   0.43    1.00
2.09    2.62    -3.14   -0.25   0.43    0.43    0.75    1.00    | 2.09    2.62    0.00    0.25    0.43    -0.43   0.75    1.00
2.09    3.14    -3.14   0.00    0.00    0.50    0.87    1.00    | 2.09    3.14    0.00    0.00    0.00    -0.50   0.87    1.00
----------------------------------------------------------------|-------------------------------------------------------------
2.62    -3.14   -3.14   0.00    0.00    0.26    0.97    1.00    | 2.62    -3.14   0.00    0.00    0.00    -0.26   0.97    1.00
2.62    -2.62   -3.14   0.43    -0.25   0.22    0.84    1.00    | 2.62    -2.62   0.00    -0.43   -0.25   -0.22   0.84    1.00
2.62    -2.09   -3.14   0.75    -0.43   0.13    0.48    1.00    | 2.62    -2.09   0.00    -0.75   -0.43   -0.13   0.48    1.00
2.62    -1.57   -3.14   0.87    -0.50   0.00    0.00    1.00    | 2.62    -1.57   0.00    -0.87   -0.50   0.00    0.00    1.00
2.62    -1.05   -3.14   0.75    -0.43   -0.13   -0.48   1.00    | 2.62    -1.05   0.00    -0.75   -0.43   0.13    -0.48   1.00
2.62    -0.52   -3.14   0.43    -0.25   -0.22   -0.84   1.00    | 2.62    -0.52   0.00    -0.43   -0.25   0.22    -0.84   1.00
2.62    0.00    -3.14   0.00    0.00    -0.26   -0.97   1.00    | 2.62    0.00    0.00    0.00    0.00    0.26    -0.97   1.00
2.62    0.52    -3.14   -0.43   0.25    -0.22   -0.84   1.00    | 2.62    0.52    0.00    0.43    0.25    0.22    -0.84   1.00
2.62    1.05    -3.14   -0.75   0.43    -0.13   -0.48   1.00    | 2.62    1.05    0.00    0.75    0.43    0.13    -0.48   1.00
2.62    1.57    -3.14   -0.87   0.50    0.00    0.00    1.00    | 2.62    1.57    0.00    0.87    0.50    0.00    0.00    1.00
2.62    2.09    -3.14   -0.75   0.43    0.13    0.48    1.00    | 2.62    2.09    0.00    0.75    0.43    -0.13   0.48    1.00
2.62    2.62    -3.14   -0.43   0.25    0.22    0.84    1.00    | 2.62    2.62    0.00    0.43    0.25    -0.22   0.84    1.00
2.62    3.14    -3.14   0.00    0.00    0.26    0.97    1.00    | 2.62    3.14    0.00    0.00    0.00    -0.26   0.97    1.00
----------------------------------------------------------------|-------------------------------------------------------------
3.14    -3.14   -3.14   0.00    0.00    0.00    1.00    1.00    | 3.14    -3.14   0.00    0.00    0.00    0.00    1.00    1.00
3.14    -2.62   -3.14   0.50    0.00    0.00    0.87    1.00    | 3.14    -2.62   0.00    -0.50   0.00    0.00    0.87    1.00
3.14    -2.09   -3.14   0.87    0.00    0.00    0.50    1.00    | 3.14    -2.09   0.00    -0.87   0.00    0.00    0.50    1.00
3.14    -1.57   -3.14   1.00    0.00    0.00    0.00    1.00    | 3.14    -1.57   0.00    -1.00   0.00    0.00    0.00    1.00
3.14    -1.05   -3.14   0.87    0.00    0.00    -0.50   1.00    | 3.14    -1.05   0.00    -0.87   0.00    0.00    -0.50   1.00
3.14    -0.52   -3.14   0.50    0.00    0.00    -0.87   1.00    | 3.14    -0.52   0.00    -0.50   0.00    0.00    -0.87   1.00
3.14    0.00    -3.14   0.00    0.00    0.00    -1.00   1.00    | 3.14    0.00    0.00    0.00    0.00    0.00    -1.00   1.00
3.14    0.52    -3.14   -0.50   0.00    0.00    -0.87   1.00    | 3.14    0.52    0.00    0.50    0.00    0.00    -0.87   1.00
3.14    1.05    -3.14   -0.87   0.00    0.00    -0.50   1.00    | 3.14    1.05    0.00    0.87    0.00    0.00    -0.50   1.00
3.14    1.57    -3.14   -1.00   0.00    0.00    0.00    1.00    | 3.14    1.57    0.00    1.00    0.00    0.00    0.00    1.00
3.14    2.09    -3.14   -0.87   0.00    0.00    0.50    1.00    | 3.14    2.09    0.00    0.87    0.00    0.00    0.50    1.00
3.14    2.62    -3.14   -0.50   0.00    0.00    0.87    1.00    | 3.14    2.62    0.00    0.50    0.00    0.00    0.87    1.00
3.14    3.14    -3.14   0.00    0.00    0.00    1.00    1.00    | 3.14    3.14    0.00    0.00    0.00    0.00    1.00    1.00

These show only t=0 and t=pi so here's a further subset that show a couple of points where 0<t<pi (just to show they also work):

Code: Select all

t=0.52                                                          | t=1.05                                                     
u       v       t       w       x       y       z       r"      | u       v       t       w       x       y       z       r" 
-3.14   -3.14   0.52    0.00    0.00    0.00    -1.00   1.00    | -3.14   -3.14   1.05    0.00    0.00    0.00    -1.00   1.00
-3.14   -2.62   0.52    -0.43   0.00    -0.25   -0.87   1.00    | -3.14   -2.62   1.05    -0.25   0.00    -0.43   -0.87   1.00
-3.14   -2.09   0.52    -0.75   0.00    -0.43   -0.50   1.00    | -3.14   -2.09   1.05    -0.43   0.00    -0.75   -0.50   1.00
-3.14   -1.57   0.52    -0.87   0.00    -0.50   0.00    1.00    | -3.14   -1.57   1.05    -0.50   0.00    -0.87   0.00    1.00
-3.14   -1.05   0.52    -0.75   0.00    -0.43   0.50    1.00    | -3.14   -1.05   1.05    -0.43   0.00    -0.75   0.50    1.00
-3.14   -0.52   0.52    -0.43   0.00    -0.25   0.87    1.00    | -3.14   -0.52   1.05    -0.25   0.00    -0.43   0.87    1.00
-3.14   0.00    0.52    0.00    0.00    0.00    1.00    1.00    | -3.14   0.00    1.05    0.00    0.00    0.00    1.00    1.00
-3.14   0.52    0.52    0.43    0.00    0.25    0.87    1.00    | -3.14   0.52    1.05    0.25    0.00    0.43    0.87    1.00
-3.14   1.05    0.52    0.75    0.00    0.43    0.50    1.00    | -3.14   1.05    1.05    0.43    0.00    0.75    0.50    1.00
-3.14   1.57    0.52    0.87    0.00    0.50    0.00    1.00    | -3.14   1.57    1.05    0.50    0.00    0.87    0.00    1.00
-3.14   2.09    0.52    0.75    0.00    0.43    -0.50   1.00    | -3.14   2.09    1.05    0.43    0.00    0.75    -0.50   1.00
-3.14   2.62    0.52    0.43    0.00    0.25    -0.87   1.00    | -3.14   2.62    1.05    0.25    0.00    0.43    -0.87   1.00
-3.14   3.14    0.52    0.00    0.00    0.00    -1.00   1.00    | -3.14   3.14    1.05    0.00    0.00    0.00    -1.00   1.00
----------------------------------------------------------------|-------------------------------------------------------------
0.00    -3.14   0.52    0.50    0.00    -0.87   0.00    1.00    | 0.00    -3.14   1.05    0.87    0.00    -0.50   0.00    1.00
0.00    -2.62   0.52    0.87    0.00    -0.50   0.00    1.00    | 0.00    -2.62   1.05    1.00    0.00    0.00    0.00    1.00
0.00    -2.09   0.52    1.00    0.00    0.00    0.00    1.00    | 0.00    -2.09   1.05    0.87    0.00    0.50    0.00    1.00
0.00    -1.57   0.52    0.87    0.00    0.50    0.00    1.00    | 0.00    -1.57   1.05    0.50    0.00    0.87    0.00    1.00
0.00    -1.05   0.52    0.50    0.00    0.87    0.00    1.00    | 0.00    -1.05   1.05    0.00    0.00    1.00    0.00    1.00
0.00    -0.52   0.52    0.00    0.00    1.00    0.00    1.00    | 0.00    -0.52   1.05    -0.50   0.00    0.87    0.00    1.00
0.00    0.00    0.52    -0.50   0.00    0.87    0.00    1.00    | 0.00    0.00    1.05    -0.87   0.00    0.50    0.00    1.00
0.00    0.52    0.52    -0.87   0.00    0.50    0.00    1.00    | 0.00    0.52    1.05    -1.00   0.00    0.00    0.00    1.00
0.00    1.05    0.52    -1.00   0.00    0.00    0.00    1.00    | 0.00    1.05    1.05    -0.87   0.00    -0.50   0.00    1.00
0.00    1.57    0.52    -0.87   0.00    -0.50   0.00    1.00    | 0.00    1.57    1.05    -0.50   0.00    -0.87   0.00    1.00
0.00    2.09    0.52    -0.50   0.00    -0.87   0.00    1.00    | 0.00    2.09    1.05    0.00    0.00    -1.00   0.00    1.00
0.00    2.62    0.52    0.00    0.00    -1.00   0.00    1.00    | 0.00    2.62    1.05    0.50    0.00    -0.87   0.00    1.00
0.00    3.14    0.52    0.50    0.00    -0.87   0.00    1.00    | 0.00    3.14    1.05    0.87    0.00    -0.50   0.00    1.00
----------------------------------------------------------------|-------------------------------------------------------------
0.52    -3.14   0.52    0.48    0.00    -0.84   0.26    1.00    | 0.52    -3.14   1.05    0.84    0.00    -0.48   0.26    1.00
0.52    -2.62   0.52    0.79    -0.25   -0.51   0.22    1.00    | 0.52    -2.62   1.05    0.94    -0.25   -0.04   0.22    1.00
0.52    -2.09   0.52    0.89    -0.43   -0.04   0.13    1.00    | 0.52    -2.09   1.05    0.79    -0.43   0.41    0.13    1.00
0.52    -1.57   0.52    0.75    -0.50   0.43    0.00    1.00    | 0.52    -1.57   1.05    0.43    -0.50   0.75    0.00    1.00
0.52    -1.05   0.52    0.41    -0.43   0.79    -0.13   1.00    | 0.52    -1.05   1.05    -0.04   -0.43   0.89    -0.13   1.00
0.52    -0.52   0.52    -0.04   -0.25   0.94    -0.22   1.00    | 0.52    -0.52   1.05    -0.51   -0.25   0.79    -0.22   1.00
0.52    0.00    0.52    -0.48   0.00    0.84    -0.26   1.00    | 0.52    0.00    1.05    -0.84   0.00    0.48    -0.26   1.00
0.52    0.52    0.52    -0.79   0.25    0.51    -0.22   1.00    | 0.52    0.52    1.05    -0.94   0.25    0.04    -0.22   1.00
0.52    1.05    0.52    -0.89   0.43    0.04    -0.13   1.00    | 0.52    1.05    1.05    -0.79   0.43    -0.41   -0.13   1.00
0.52    1.57    0.52    -0.75   0.50    -0.43   0.00    1.00    | 0.52    1.57    1.05    -0.43   0.50    -0.75   0.00    1.00
0.52    2.09    0.52    -0.41   0.43    -0.79   0.13    1.00    | 0.52    2.09    1.05    0.04    0.43    -0.89   0.13    1.00
0.52    2.62    0.52    0.04    0.25    -0.94   0.22    1.00    | 0.52    2.62    1.05    0.51    0.25    -0.79   0.22    1.00
0.52    3.14    0.52    0.48    0.00    -0.84   0.26    1.00    | 0.52    3.14    1.05    0.84    0.00    -0.48   0.26    1.00
----------------------------------------------------------------|-------------------------------------------------------------
1.05    -3.14   0.52    0.43    0.00    -0.75   0.50    1.00    | 1.05    -3.14   1.05    0.75    0.00    -0.43   0.50    1.00
1.05    -2.62   0.52    0.59    -0.43   -0.52   0.43    1.00    | 1.05    -2.62   1.05    0.77    -0.43   -0.16   0.43    1.00
1.05    -2.09   0.52    0.59    -0.75   -0.16   0.25    1.00    | 1.05    -2.09   1.05    0.59    -0.75   0.16    0.25    1.00
1.05    -1.57   0.52    0.43    -0.87   0.25    0.00    1.00    | 1.05    -1.57   1.05    0.25    -0.87   0.43    0.00    1.00
1.05    -1.05   0.52    0.16    -0.75   0.59    -0.25   1.00    | 1.05    -1.05   1.05    -0.16   -0.75   0.59    -0.25   1.00
1.05    -0.52   0.52    -0.16   -0.43   0.77    -0.43   1.00    | 1.05    -0.52   1.05    -0.52   -0.43   0.59    -0.43   1.00
1.05    0.00    0.52    -0.43   0.00    0.75    -0.50   1.00    | 1.05    0.00    1.05    -0.75   0.00    0.43    -0.50   1.00
1.05    0.52    0.52    -0.59   0.43    0.52    -0.43   1.00    | 1.05    0.52    1.05    -0.77   0.43    0.16    -0.43   1.00
1.05    1.05    0.52    -0.59   0.75    0.16    -0.25   1.00    | 1.05    1.05    1.05    -0.59   0.75    -0.16   -0.25   1.00
1.05    1.57    0.52    -0.43   0.87    -0.25   0.00    1.00    | 1.05    1.57    1.05    -0.25   0.87    -0.43   0.00    1.00
1.05    2.09    0.52    -0.16   0.75    -0.59   0.25    1.00    | 1.05    2.09    1.05    0.16    0.75    -0.59   0.25    1.00
1.05    2.62    0.52    0.16    0.43    -0.77   0.43    1.00    | 1.05    2.62    1.05    0.52    0.43    -0.59   0.43    1.00
1.05    3.14    0.52    0.43    0.00    -0.75   0.50    1.00    | 1.05    3.14    1.05    0.75    0.00    -0.43   0.50    1.00
----------------------------------------------------------------|-------------------------------------------------------------
1.57    -3.14   0.52    0.35    0.00    -0.61   0.71    1.00    | 1.57    -3.14   1.05    0.61    0.00    -0.35   0.71    1.00
1.57    -2.62   0.52    0.31    -0.50   -0.53   0.61    1.00    | 1.57    -2.62   1.05    0.53    -0.50   -0.31   0.61    1.00
1.57    -2.09   0.52    0.18    -0.87   -0.31   0.35    1.00    | 1.57    -2.09   1.05    0.31    -0.87   -0.18   0.35    1.00
1.57    -1.57   0.52    0.00    -1.00   0.00    0.00    1.00    | 1.57    -1.57   1.05    0.00    -1.00   0.00    0.00    1.00
1.57    -1.05   0.52    -0.18   -0.87   0.31    -0.35   1.00    | 1.57    -1.05   1.05    -0.31   -0.87   0.18    -0.35   1.00
1.57    -0.52   0.52    -0.31   -0.50   0.53    -0.61   1.00    | 1.57    -0.52   1.05    -0.53   -0.50   0.31    -0.61   1.00
1.57    0.00    0.52    -0.35   0.00    0.61    -0.71   1.00    | 1.57    0.00    1.05    -0.61   0.00    0.35    -0.71   1.00
1.57    0.52    0.52    -0.31   0.50    0.53    -0.61   1.00    | 1.57    0.52    1.05    -0.53   0.50    0.31    -0.61   1.00
1.57    1.05    0.52    -0.18   0.87    0.31    -0.35   1.00    | 1.57    1.05    1.05    -0.31   0.87    0.18    -0.35   1.00
1.57    1.57    0.52    0.00    1.00    0.00    0.00    1.00    | 1.57    1.57    1.05    0.00    1.00    0.00    0.00    1.00
1.57    2.09    0.52    0.18    0.87    -0.31   0.35    1.00    | 1.57    2.09    1.05    0.31    0.87    -0.18   0.35    1.00
1.57    2.62    0.52    0.31    0.50    -0.53   0.61    1.00    | 1.57    2.62    1.05    0.53    0.50    -0.31   0.61    1.00
1.57    3.14    0.52    0.35    0.00    -0.61   0.71    1.00    | 1.57    3.14    1.05    0.61    0.00    -0.35   0.71    1.00
----------------------------------------------------------------|-------------------------------------------------------------
2.09    -3.14   0.52    0.25    0.00    -0.43   0.87    1.00    | 2.09    -3.14   1.05    0.43    0.00    -0.25   0.87    1.00
2.09    -2.62   0.52    0.00    -0.43   -0.50   0.75    1.00    | 2.09    -2.62   1.05    0.25    -0.43   -0.43   0.75    1.00
2.09    -2.09   0.52    -0.25   -0.75   -0.43   0.43    1.00    | 2.09    -2.09   1.05    0.00    -0.75   -0.50   0.43    1.00
2.09    -1.57   0.52    -0.43   -0.87   -0.25   0.00    1.00    | 2.09    -1.57   1.05    -0.25   -0.87   -0.43   0.00    1.00
2.09    -1.05   0.52    -0.50   -0.75   0.00    -0.43   1.00    | 2.09    -1.05   1.05    -0.43   -0.75   -0.25   -0.43   1.00
2.09    -0.52   0.52    -0.43   -0.43   0.25    -0.75   1.00    | 2.09    -0.52   1.05    -0.50   -0.43   0.00    -0.75   1.00
2.09    0.00    0.52    -0.25   0.00    0.43    -0.87   1.00    | 2.09    0.00    1.05    -0.43   0.00    0.25    -0.87   1.00
2.09    0.52    0.52    0.00    0.43    0.50    -0.75   1.00    | 2.09    0.52    1.05    -0.25   0.43    0.43    -0.75   1.00
2.09    1.05    0.52    0.25    0.75    0.43    -0.43   1.00    | 2.09    1.05    1.05    0.00    0.75    0.50    -0.43   1.00
2.09    1.57    0.52    0.43    0.87    0.25    0.00    1.00    | 2.09    1.57    1.05    0.25    0.87    0.43    0.00    1.00
2.09    2.09    0.52    0.50    0.75    0.00    0.43    1.00    | 2.09    2.09    1.05    0.43    0.75    0.25    0.43    1.00
2.09    2.62    0.52    0.43    0.43    -0.25   0.75    1.00    | 2.09    2.62    1.05    0.50    0.43    0.00    0.75    1.00
2.09    3.14    0.52    0.25    0.00    -0.43   0.87    1.00    | 2.09    3.14    1.05    0.43    0.00    -0.25   0.87    1.00
----------------------------------------------------------------|-------------------------------------------------------------
2.62    -3.14   0.52    0.13    0.00    -0.22   0.97    1.00    | 2.62    -3.14   1.05    0.22    0.00    -0.13   0.97    1.00
2.62    -2.62   0.52    -0.26   -0.25   -0.41   0.84    1.00    | 2.62    -2.62   1.05    -0.02   -0.25   -0.49   0.84    1.00
2.62    -2.09   0.52    -0.58   -0.43   -0.49   0.48    1.00    | 2.62    -2.09   1.05    -0.26   -0.43   -0.71   0.48    1.00
2.62    -1.57   0.52    -0.75   -0.50   -0.43   0.00    1.00    | 2.62    -1.57   1.05    -0.43   -0.50   -0.75   0.00    1.00
2.62    -1.05   0.52    -0.71   -0.43   -0.26   -0.48   1.00    | 2.62    -1.05   1.05    -0.49   -0.43   -0.58   -0.48   1.00
2.62    -0.52   0.52    -0.49   -0.25   -0.02   -0.84   1.00    | 2.62    -0.52   1.05    -0.41   -0.25   -0.26   -0.84   1.00
2.62    0.00    0.52    -0.13   0.00    0.22    -0.97   1.00    | 2.62    0.00    1.05    -0.22   0.00    0.13    -0.97   1.00
2.62    0.52    0.52    0.26    0.25    0.41    -0.84   1.00    | 2.62    0.52    1.05    0.02    0.25    0.49    -0.84   1.00
2.62    1.05    0.52    0.58    0.43    0.49    -0.48   1.00    | 2.62    1.05    1.05    0.26    0.43    0.71    -0.48   1.00
2.62    1.57    0.52    0.75    0.50    0.43    0.00    1.00    | 2.62    1.57    1.05    0.43    0.50    0.75    0.00    1.00
2.62    2.09    0.52    0.71    0.43    0.26    0.48    1.00    | 2.62    2.09    1.05    0.49    0.43    0.58    0.48    1.00
2.62    2.62    0.52    0.49    0.25    0.02    0.84    1.00    | 2.62    2.62    1.05    0.41    0.25    0.26    0.84    1.00
2.62    3.14    0.52    0.13    0.00    -0.22   0.97    1.00    | 2.62    3.14    1.05    0.22    0.00    -0.13   0.97    1.00
----------------------------------------------------------------|-------------------------------------------------------------
3.14    -3.14   0.52    0.00    0.00    0.00    1.00    1.00    | 3.14    -3.14   1.05    0.00    0.00    0.00    1.00    1.00
3.14    -2.62   0.52    -0.43   0.00    -0.25   0.87    1.00    | 3.14    -2.62   1.05    -0.25   0.00    -0.43   0.87    1.00
3.14    -2.09   0.52    -0.75   0.00    -0.43   0.50    1.00    | 3.14    -2.09   1.05    -0.43   0.00    -0.75   0.50    1.00
3.14    -1.57   0.52    -0.87   0.00    -0.50   0.00    1.00    | 3.14    -1.57   1.05    -0.50   0.00    -0.87   0.00    1.00
3.14    -1.05   0.52    -0.75   0.00    -0.43   -0.50   1.00    | 3.14    -1.05   1.05    -0.43   0.00    -0.75   -0.50   1.00
3.14    -0.52   0.52    -0.43   0.00    -0.25   -0.87   1.00    | 3.14    -0.52   1.05    -0.25   0.00    -0.43   -0.87   1.00
3.14    0.00    0.52    0.00    0.00    0.00    -1.00   1.00    | 3.14    0.00    1.05    0.00    0.00    0.00    -1.00   1.00
3.14    0.52    0.52    0.43    0.00    0.25    -0.87   1.00    | 3.14    0.52    1.05    0.25    0.00    0.43    -0.87   1.00
3.14    1.05    0.52    0.75    0.00    0.43    -0.50   1.00    | 3.14    1.05    1.05    0.43    0.00    0.75    -0.50   1.00
3.14    1.57    0.52    0.87    0.00    0.50    0.00    1.00    | 3.14    1.57    1.05    0.50    0.00    0.87    0.00    1.00
3.14    2.09    0.52    0.75    0.00    0.43    0.50    1.00    | 3.14    2.09    1.05    0.43    0.00    0.75    0.50    1.00
3.14    2.62    0.52    0.43    0.00    0.25    0.87    1.00    | 3.14    2.62    1.05    0.25    0.00    0.43    0.87    1.00
3.14    3.14    0.52    0.00    0.00    0.00    1.00    1.00    | 3.14    3.14    1.05    0.00    0.00    0.00    1.00    1.00

All of the varieties and steps produce resultant radii that are equal to 1.

I would certainly like to see alternate equations that may be better if we can work some out...

[Teragon]

I did up a spreadsheet to quickly test your new formulations.
To test this I set the R=0 and n=1 for your equations. I also set r=1 just to get unit circles.

Good idea and yes, there where mistakes in the code. I changed it in the post above. Could you test it again now?

Related to my major mistake of writing w = r was my notion that the 0° Moebius strip was just an extruded usual Moebius strip. This would give the torus a quadratic cross section, whereas in reality, it has a circular cross section.