Why Humans Will Never Understand 4D Space
46 posts
• Page 1 of 2 • 1, 2
Why Humans Will Never Understand 4D Space
See http://bit.ly/2frZJST to understand why Humans will never understand 4D Space.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
I think you're giving up too soon, Steve. It has nothing to do with being smart enough. It's the amount of time you put into it. You might find that the people who have a very good grasp of +4D geometry have been studying it for more than 5~10 years.
The type/level of math one has access to can also be a limiting factor, which relates to the sophistication of the visuals one can make (the diff between an approximation of your 'best guess', and a direct mathematical output of a function, for some hypershape) Another thing that can happen is not enough collaboration with others who study the same thing. Often times, you'll run into a barrier in reasoning, when it just doesn't make any sense. This is when a lot of people give up, when they should be posting more questions than they have answers for.
Instead of "Just give up everyone, it's impossible!" , maybe try a "Alright, this is as far as I can go with my reasoning. Anyone have an idea, or a visual that might help?" . One leads to greater knowledge, the other does not.
We are embedded in a 3D physical reality, this is true. Any attempt to grasp a 4D object is met with great resistance for some time. But, you can still use a little 3D intuition and 2D -> 3D analogy to help the process. The truth is, a 4D physical object is about as alien as it gets. They're truly alien to our 3D understanding. We will never come across anything like a tesseract passing through a 3-plane. But, we can create a tesseract in 3D slices (or 3D projection) and play around with it, on a computer.
In addition to that, the very best way to study such a thing is to reduce these different n-D shapes into a math expression, and work out the finer details from it. On this forum, there are several forms of math that do this. This method is far superior to visual-only, or best guesses. The exploration you've taken is a great intro that will help with further study. You've got the basic concept down, regarding how flat a 3D object is in a 4D space. That's further along than most other people.
So, don't stop here with your interest. I also recommend giving yourself some mental breaks from such intense studying/visualizing. It is exhausting, trying to imagine something clearly for the first time. Your mind can't always be 'on' the whole time.
The type/level of math one has access to can also be a limiting factor, which relates to the sophistication of the visuals one can make (the diff between an approximation of your 'best guess', and a direct mathematical output of a function, for some hypershape) Another thing that can happen is not enough collaboration with others who study the same thing. Often times, you'll run into a barrier in reasoning, when it just doesn't make any sense. This is when a lot of people give up, when they should be posting more questions than they have answers for.
Instead of "Just give up everyone, it's impossible!" , maybe try a "Alright, this is as far as I can go with my reasoning. Anyone have an idea, or a visual that might help?" . One leads to greater knowledge, the other does not.
We are embedded in a 3D physical reality, this is true. Any attempt to grasp a 4D object is met with great resistance for some time. But, you can still use a little 3D intuition and 2D -> 3D analogy to help the process. The truth is, a 4D physical object is about as alien as it gets. They're truly alien to our 3D understanding. We will never come across anything like a tesseract passing through a 3-plane. But, we can create a tesseract in 3D slices (or 3D projection) and play around with it, on a computer.
In addition to that, the very best way to study such a thing is to reduce these different n-D shapes into a math expression, and work out the finer details from it. On this forum, there are several forms of math that do this. This method is far superior to visual-only, or best guesses. The exploration you've taken is a great intro that will help with further study. You've got the basic concept down, regarding how flat a 3D object is in a 4D space. That's further along than most other people.
So, don't stop here with your interest. I also recommend giving yourself some mental breaks from such intense studying/visualizing. It is exhausting, trying to imagine something clearly for the first time. Your mind can't always be 'on' the whole time.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Why Humans Will Never Understand 4D Space
While our physical senses will never see 4D directly, nothing theoretically prevents us from mentally grasping it.
Case in point: we actually cannot see 3D. Our eyes only have 2D retinas, which can only capture 2D projections of 3D objects, so what we're actually seeing every day isn't 3D at all, but merely 2D projections of the surfaces of 3D objects. Nevertheless, our brain has no problem at all in constructing 3D models of the world that are, in spite of certain borderline flaws, pretty darn accurate. All the 3D that you imagine you see every day, is actually a mental construct produced by your brain trying to reconcile the binocular disparity between the 2D images that your two eyes see! In fact, your brain does this so well that you don't even have to think about it, you just instinctively interpret these 2D images in a 3D way.
It is definitely possible to learn to "visualize" 4D mentally. It takes some effort, but it's quite possible. True, it probably will never attain to the same level as a hypothetical 4D being with 4D eyes (that can see 3D projections of 4D objects), and it will probably never become instinctive in the same way 3D is instinctive, but it's possible to get pretty darned good with it. Good enough for me to (re)discover quite a number of 4D objects, in fact, that afterwards were verified to be correct mathematically.
Case in point: we actually cannot see 3D. Our eyes only have 2D retinas, which can only capture 2D projections of 3D objects, so what we're actually seeing every day isn't 3D at all, but merely 2D projections of the surfaces of 3D objects. Nevertheless, our brain has no problem at all in constructing 3D models of the world that are, in spite of certain borderline flaws, pretty darn accurate. All the 3D that you imagine you see every day, is actually a mental construct produced by your brain trying to reconcile the binocular disparity between the 2D images that your two eyes see! In fact, your brain does this so well that you don't even have to think about it, you just instinctively interpret these 2D images in a 3D way.
It is definitely possible to learn to "visualize" 4D mentally. It takes some effort, but it's quite possible. True, it probably will never attain to the same level as a hypothetical 4D being with 4D eyes (that can see 3D projections of 4D objects), and it will probably never become instinctive in the same way 3D is instinctive, but it's possible to get pretty darned good with it. Good enough for me to (re)discover quite a number of 4D objects, in fact, that afterwards were verified to be correct mathematically.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Why Humans Will Never Understand 4D Space
In fact, the best way to get from grasping one dimension towards the next, is by considering prisms or pyramids of things of the lesser dimension. This once let me to the inventon of segmentotopes, i.e. monostratic orbiform polytopes. Those are defined to be polytopes with unit edges only, where all vertices are contained within a pair of parallel hyperplanes, and also are on a hypersphere. Those pyrmaids and prisms then are just a special case of these. - These segmentotopes are just being designed to be easily being grasped from the underlying dimension of the bases.
Having managed that step, then one could aim to conquer multistratic figures also. Or even could apply that cross dimensional step over and over again, thereby climbing into ever higher dimensions!
Thus, I fully second what Quickfur just said.
--- rk
Having managed that step, then one could aim to conquer multistratic figures also. Or even could apply that cross dimensional step over and over again, thereby climbing into ever higher dimensions!
Thus, I fully second what Quickfur just said.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Why Humans Will Never Understand 4D Space
What you see is only part of the picture. The mind does a good deal of processing, and it is easy enough to trick this process. It apparently takes learning for us to read pictures, even photographs. It is probably different of movies, but for still pictures, we need apparently to be taught these things. Laurence of Arabia, for having presented some Arabs a group painting of themselves, the arabs were unable to decipher the picture into visual clues that they were people, and asked were such a spot the camel's nose.
If you wear glasses, at a different prescription to your want, then things will be seen and read further away or closer than normal, and you will act accordingly. You should also note that optical illusions also work by tricking the mind to something that the eye reads separately.
4D space, is not so much building a holographic picture in your eye, but tricking the mind into reading what is in front of it, is actually a holographic view of the 3d image of 4d. If you look at some of quickfur's pictures, especially the stereo pairs, the mind would be tricked into building a foam of cells. This is what quickfur draws. But we can as readily read a foam of polygons into a picture of a polyhedron, and if we know the foam of cells are polyhedra forshortened by sloping, we can appreciate four dimensions.
And this is the trick. The mind may, or may not actually create a visual of 4d, but one can build a thing of changing scenes, which to the mind is 4d.
And we can well understand spaces of 4D or 5D or 6D, with a degree of understanding of the mind, and a good deal of help from the eye.
If you wear glasses, at a different prescription to your want, then things will be seen and read further away or closer than normal, and you will act accordingly. You should also note that optical illusions also work by tricking the mind to something that the eye reads separately.
4D space, is not so much building a holographic picture in your eye, but tricking the mind into reading what is in front of it, is actually a holographic view of the 3d image of 4d. If you look at some of quickfur's pictures, especially the stereo pairs, the mind would be tricked into building a foam of cells. This is what quickfur draws. But we can as readily read a foam of polygons into a picture of a polyhedron, and if we know the foam of cells are polyhedra forshortened by sloping, we can appreciate four dimensions.
And this is the trick. The mind may, or may not actually create a visual of 4d, but one can build a thing of changing scenes, which to the mind is 4d.
And we can well understand spaces of 4D or 5D or 6D, with a degree of understanding of the mind, and a good deal of help from the eye.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Why Humans Will Never Understand 4D Space
I love the thought of 4D space. I just wish I had more time to spend there...
For me it was a case of understanding the relevance and nature of extra side-ways and the relation of those to our common actions.
Common actions include moving forward and backward and gravitational downwards or the opposite upwards.
These tend to be common to all numbers of spatial dimensions where something might occur (ie. 2D and above).
We will tend to want to do things in relation to these 4 directions no matter which nD universe we are in.
For example: trees will always grow mainly upwards. Also, we will still need to travel towards destinations.
My approach to understanding extra-sideways is to rotate the extra dimensions around our own.
For a 2Der they would take a rotation of sideways slices of our 3D world and rotate them instead vertically in their own.
For us we would take a rotation of slices of a 4D world and rotate them vertically in our 3D space.
There is going to be crowding when there are a lot of 4D objects but it gives us somewhere to consider them.
We can then just think of the bulk as the sum of all these rotations.
It is this which allows me to more readily see a 4Ders world and predict what would eventuate; which I couldn't do originally when I first started.
This approach helps me to avoid the mistakes that are easy to make when we think from our, only really available, 3D experience...
It helps me to more easily describe the world of a 4Der and what 4D would actually mean that is different or similar to what we have.
That is an exciting thing to do!
For me it is more about the day to day gritty things of the 4Der's life and how their life would be the same or different to ours...
For me it was a case of understanding the relevance and nature of extra side-ways and the relation of those to our common actions.
Common actions include moving forward and backward and gravitational downwards or the opposite upwards.
These tend to be common to all numbers of spatial dimensions where something might occur (ie. 2D and above).
We will tend to want to do things in relation to these 4 directions no matter which nD universe we are in.
For example: trees will always grow mainly upwards. Also, we will still need to travel towards destinations.
My approach to understanding extra-sideways is to rotate the extra dimensions around our own.
For a 2Der they would take a rotation of sideways slices of our 3D world and rotate them instead vertically in their own.
For us we would take a rotation of slices of a 4D world and rotate them vertically in our 3D space.
There is going to be crowding when there are a lot of 4D objects but it gives us somewhere to consider them.
We can then just think of the bulk as the sum of all these rotations.
It is this which allows me to more readily see a 4Ders world and predict what would eventuate; which I couldn't do originally when I first started.
This approach helps me to avoid the mistakes that are easy to make when we think from our, only really available, 3D experience...
It helps me to more easily describe the world of a 4Der and what 4D would actually mean that is different or similar to what we have.
That is an exciting thing to do!
For me it is more about the day to day gritty things of the 4Der's life and how their life would be the same or different to ours...
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Why Humans Will Never Understand 4D Space
I do know a way, but it may be you won''t like it. Does it fit with the requirement that we will never understand 4D? If it doesn't fit where should I write to? It takes a long time for me to write. Studying previous comments especially ICN5D. Depends on how one defines what constitutes "dimension" possibly.
All sense impressions are encoded using identical nerve impulses that create the qualities of the world we "know". It is taking place in our brains, these patterns of impulses and the connections created by them, are recoded through our history to form words that represent these qualities, these words we can use to "think" with and communicate with and store.
They may mean different things to different people.
Spacial dimensions are mutually at right angles to each other. This, if correct, means what follows might be correct.
From my viewpoint front/back, left/right, up/down form the first three directions. They have the following qualities -
They are of indefinite length. They can in combination define all intermediate directions. If a direction is a vector then
They either diverge from a point or converge to a point or cross at a point. This point can be called an "Identity". I am one such identity though the meaning of 'point' has been stretched and may not apply. I cannot see these directions, they are lines of sight LoS. I see along these directions. I believe they are there. They are special to every identity. Imaginary, created by the brain. Visualisable.
Difficult bit here. A sphere cantered on the Identity is at right angles to every LoS as are all spheres no matter what the radius. This complies with the mutuality. The mind is capable of visualising this 4D interpretation, providing the meaning of the word "dimension" can be extended. If it is accepted, then the world I am conscious of is just that 4th dimension for I can't see my Identity or my LoSs. For a conscious being we have to accept ones own Identity as unique, with all other entities having their own Identity unique to them. If this is barking mad, please do not accept anything else.
To boil it down to its simplest form, the two lines at right angles joined by an arc are three dimensions. The arc is a third dimension defining a surface. It seems crazy. I look at it over and over. It mucks up all my beliefs about multidimensional shapes but my brain keeps saying why not?
I would be most pleased if someone could convert me back.
If it is acceptable, it results in a nearly visualisable 5th to do with motion which in turn alters ones perception of time. Perhaps this is playing with words, but it does match ones perception of the world and destroy every frame of reference I have encountere.
Identity
All sense impressions are encoded using identical nerve impulses that create the qualities of the world we "know". It is taking place in our brains, these patterns of impulses and the connections created by them, are recoded through our history to form words that represent these qualities, these words we can use to "think" with and communicate with and store.
They may mean different things to different people.
Spacial dimensions are mutually at right angles to each other. This, if correct, means what follows might be correct.
From my viewpoint front/back, left/right, up/down form the first three directions. They have the following qualities -
They are of indefinite length. They can in combination define all intermediate directions. If a direction is a vector then
They either diverge from a point or converge to a point or cross at a point. This point can be called an "Identity". I am one such identity though the meaning of 'point' has been stretched and may not apply. I cannot see these directions, they are lines of sight LoS. I see along these directions. I believe they are there. They are special to every identity. Imaginary, created by the brain. Visualisable.
Difficult bit here. A sphere cantered on the Identity is at right angles to every LoS as are all spheres no matter what the radius. This complies with the mutuality. The mind is capable of visualising this 4D interpretation, providing the meaning of the word "dimension" can be extended. If it is accepted, then the world I am conscious of is just that 4th dimension for I can't see my Identity or my LoSs. For a conscious being we have to accept ones own Identity as unique, with all other entities having their own Identity unique to them. If this is barking mad, please do not accept anything else.
To boil it down to its simplest form, the two lines at right angles joined by an arc are three dimensions. The arc is a third dimension defining a surface. It seems crazy. I look at it over and over. It mucks up all my beliefs about multidimensional shapes but my brain keeps saying why not?
I would be most pleased if someone could convert me back.
If it is acceptable, it results in a nearly visualisable 5th to do with motion which in turn alters ones perception of time. Perhaps this is playing with words, but it does match ones perception of the world and destroy every frame of reference I have encountere.
Identity
- Richard T H Ellis
- Nullonian
- Posts: 1
- Joined: Thu Dec 15, 2016 9:53 pm
Re: Why Humans Will Never Understand 4D Space
Though... I did just realise that I shouldn't be rotating the up direction with the sideways rotation...
This then gives the characteristic turning in on itself that has always been demonstrated on this forum...
Hmmm, what will that mean for what I was thinking?
I only realised that when I was trying to design a 4D chain and I knew there was something wrong!
This then gives the characteristic turning in on itself that has always been demonstrated on this forum...
Hmmm, what will that mean for what I was thinking?
I only realised that when I was trying to design a 4D chain and I knew there was something wrong!
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Why Humans Will Never Understand 4D Space
In 2D we can't have chains because there is no sideways. So we are reliant on a series of S-hooks or alternating C-hooks.
In 3D we can have proper chains made of alternating O's locked together.
In 4D we can have a linear hole along one dimension and in a second linear dimension for the alternating links.
And we would still have the linear direction of the length of he chain; as in our world.
But that leaves one linear dimension - or circle of dimensions - to fulfill to prevent unlinking...
Does that mean we would need to combine both the 2D and 3D worlds and have a link and hooking system working together?
Or, one of the fellows on here invented semi-rail cars.
So alternatively, could we do something similar and use some sort of incorporated guide channels to lock the chain along the two perpendicular alignments allowing the chain to work?
In 3D we can have proper chains made of alternating O's locked together.
In 4D we can have a linear hole along one dimension and in a second linear dimension for the alternating links.
And we would still have the linear direction of the length of he chain; as in our world.
But that leaves one linear dimension - or circle of dimensions - to fulfill to prevent unlinking...
Does that mean we would need to combine both the 2D and 3D worlds and have a link and hooking system working together?
Or, one of the fellows on here invented semi-rail cars.
So alternatively, could we do something similar and use some sort of incorporated guide channels to lock the chain along the two perpendicular alignments allowing the chain to work?
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Why Humans Will Never Understand 4D Space
ICN5D wrote:I think you're giving up too soon, Steve.
First of all thank you for that well thought out reply. Secondly, sorry about this very late response. I guess I didn't say what really convinced me that we 3D Beings will never understand 4D. It was the insight I got while thinking about how a 2D Being might understand 3D Space. Because I am 3D I should be able to show the 2D Being how to do it. The futility of a 2D Being understanding 3D became clear to me. The 2D Being is stuck in his 2D Space. All he can ever do is look at intersections and slices. He can arrange the slices all around in his 2D Space but can never truly see the slices connected together into 3D Space. He is truly handicapped by 2d thinking. He is unable, physically, to find that third direction that he needs to put the slices together to form a 3D object. Then his visual system will not allow him to ever see a 3D object. The 2D Being needs to be able to see a 2D Hyper plane object, a square for example, the way we see it. He needs to see the insides of it. I think understanding the dilemma for the 2D Being should give insight into our problem. Slices and reflections don't do it for me anymore, I need something better. It has to be a Visualization answer. I'm pretty good with math and I don't think I would be very fulfilled by a purely Math answer. Show me how to see a 3D Hyper Plane. Show me how to see all the points of a solid cube at the same time, all connected together without being sliced up.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Slices, intersections and reflections don't do it for me anymore. For example I want to see all the points of a 3D cube simultaneously with all the connections between points to other points without slicing it up. It must also seem flat in this visualization that I am looking for. Can you really do that?quickfur wrote:While our physical senses will never see 4D directly, nothing theoretically prevents us from mentally grasping it.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Can you really see all the points of a solid 3D cube at the same time while seeing all the connections and without slicing the thing up? It must also give the sensation of a flat object. I don't think anybody can do that. But this is the requirement I put on my study. I was not able to do it.wendy wrote:What you see is only part of the picture.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
But can you really see a single 3D Hyper Plane like a 4D Being would? I'm interested in knowing how you do that.Klitzing wrote:In fact, the best way to get from grasping one dimension towards the next, is by considering prisms or pyramids of things of the lesser dimension.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
By rotating the extra dimension into our 3D Space you are doing what I did in my animations. It works for a period of time but eventually I needed more. You need to see all the point of a solid 3D cube simultaneously while seeing all the connections of the points to each other and not slicing things up and it must have the sense of being flat.gonegahgah wrote:I love the thought of 4D space. I just wish I had more time to spend there...
For me it was a case of understanding the relevance and nature of extra side-ways and the relation of those to our common actions.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
I agree, simply slicing 3D bodies and viewing disconnected slices as some series does not provide a good understanding of 3D by means of simple 2D objects.
Right for that purpose Viktor Schlegel once invented the Schlegel diagrams. These diagrams are a mere edge diagram of the according polyhedron, seen from very close above one of its faces, everything then being projected into this very face. E.g. a cube then would look more or less like this:
Even so the lacing faces get distorted here, it provides a very good understanding of the full figure. Also the complete incidence structure is faithfully transfered.
The same then holds true for projection from 4D down into 3D. There too Schlegel diagrams provide good insights. The only disadventage here usually is, that pictures ask for a further projection down to 2D. So it might serve usefull to use a stereo pair of 3D projections being further projected slightly different into 2D. Or you better would use true 3D devices like VRML models, which allow for interactive rotations on the screen.
But even a single 2D picture of a 3D Schlegel diagram of a 4D polychoron serves much better to the grasp of its structure than mere sectioning series would, I think. Esp. whenever you would not have too many vertex layers to be projected from 4D into 3D. - This was why I once invented the set of segmentotopes right for educational purposes: polytopes which have unit edges throughout only, and all their vertices being located both on a hypersphere (that is, the polytope is orbiform) and on a pair of parallel hyperplanes (that is, within orthogonal direction we just have 2 vertex layers). This then allows for very simple to grasp Schlegel diagrams (when projected along this orthogonal direction).
I'd think, you easily would grasp all the needed cells e.g. for that exeptional segmentochoron K-4.21 (cube||ike):
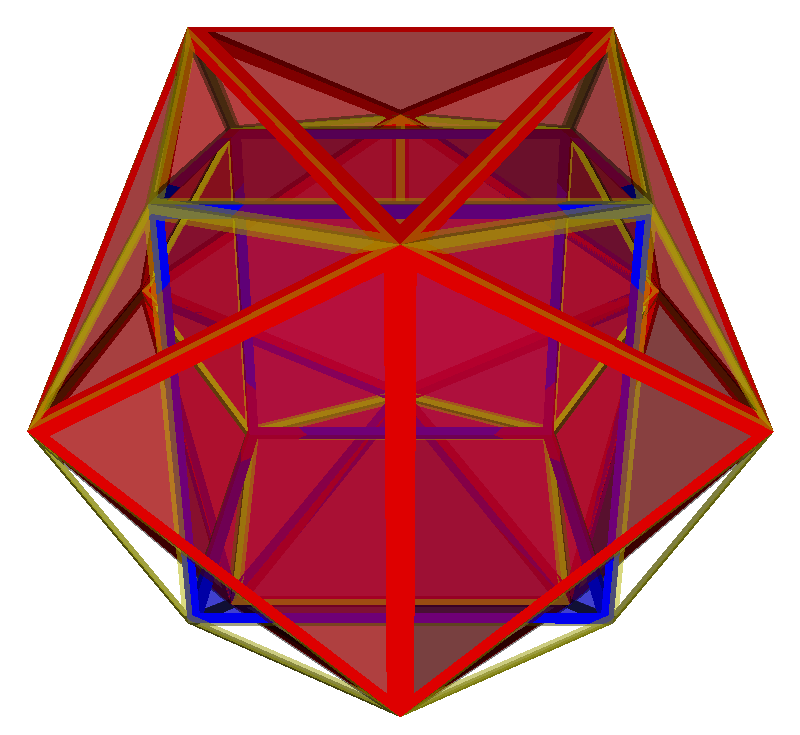
The one layer shows the blue cube, the other one the red icosahedron (ike). Lacing faces then are 6 triangular prisms (square-attached to the faces of the cube), 12 square pyramids (square-attached to the other squares of those triangle prisms), and 8 tetrahedra (tip-to-tip with the vertices of the cube).
Being equipped with such an aid, I'd say it is well possible to get rather good mental models of 4D objects for mere 3D humans!![Pleased :]](./images/smilies/pleased.gif)
--- rk
Right for that purpose Viktor Schlegel once invented the Schlegel diagrams. These diagrams are a mere edge diagram of the according polyhedron, seen from very close above one of its faces, everything then being projected into this very face. E.g. a cube then would look more or less like this:
- Code: Select all
*---------------*
| \ / |
| *-------* |
| | | |
| | | |
| | | |
| *-------* |
| / \ |
*---------------*
Even so the lacing faces get distorted here, it provides a very good understanding of the full figure. Also the complete incidence structure is faithfully transfered.
The same then holds true for projection from 4D down into 3D. There too Schlegel diagrams provide good insights. The only disadventage here usually is, that pictures ask for a further projection down to 2D. So it might serve usefull to use a stereo pair of 3D projections being further projected slightly different into 2D. Or you better would use true 3D devices like VRML models, which allow for interactive rotations on the screen.
But even a single 2D picture of a 3D Schlegel diagram of a 4D polychoron serves much better to the grasp of its structure than mere sectioning series would, I think. Esp. whenever you would not have too many vertex layers to be projected from 4D into 3D. - This was why I once invented the set of segmentotopes right for educational purposes: polytopes which have unit edges throughout only, and all their vertices being located both on a hypersphere (that is, the polytope is orbiform) and on a pair of parallel hyperplanes (that is, within orthogonal direction we just have 2 vertex layers). This then allows for very simple to grasp Schlegel diagrams (when projected along this orthogonal direction).
I'd think, you easily would grasp all the needed cells e.g. for that exeptional segmentochoron K-4.21 (cube||ike):

The one layer shows the blue cube, the other one the red icosahedron (ike). Lacing faces then are 6 triangular prisms (square-attached to the faces of the cube), 12 square pyramids (square-attached to the other squares of those triangle prisms), and 8 tetrahedra (tip-to-tip with the vertices of the cube).
Being equipped with such an aid, I'd say it is well possible to get rather good mental models of 4D objects for mere 3D humans!
![Pleased :]](./images/smilies/pleased.gif)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Why Humans Will Never Understand 4D Space
SteveKlinko wrote: wendy wrote:
What you see is only part of the picture.
Can you really see all the points of a solid 3D cube at the same time while seeing all the connections and without slicing the thing up? It must also give the sensation of a flat object. I don't think anybody can do that. But this is the requirement I put on my study. I was not able to do it.
The funny part about this is that we can't even see three dimensions. It's a learnt art from running into things, and if one might change the focal lengths of one's glasses, things are seen at a different distance to what they really are. All the same, i figured out the clifford rotations by watching the night sky in four dimensions.
The reality is that the eye sees things, it's up to the brain to figure out what has been seen. We miss a large amount of 3d things because the mind closes triangles, and puts items closer to what is supposed to be there. A really good experiment is in Betty Edward's art of drawing. Take a picture from a news-paper, and in one attempt, try to copy it (not trace it), onto a sketch pad. Then do the same thing with the picture upside down. The difference is mind-opening.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Why Humans Will Never Understand 4D Space
I Googled the name of your second figure to learn more about it. I can see that you have done a lot of good work on these topics. I do appreciate the approach that you take, because it does provide a certain way of visualizing these things. But I am simple minded and I have to understand the first more simple principles of methods and theories before I can move on to more complicated aspects. I admit I am stuck on the 3D Hyper Plane and feel that I cant move forward without understanding it better. I understand it conceptually but I want to understand it like a 4Der would, which to me is the next logical step. I am looking for a representation for the cube that will give me the insight that a 4Der would have. First the cube would be flat. Your diagram shows that, but things are overlapped. The 4Der would not see any overlap as long as he is looking at the cube from outside our 3D Space. Next thing is that the six faces of the cube would all look the same size and shape and would surround the inside points in some way. All points of the cube, even a solid cube, would be visible and unobstructed by any other points of the cube. The 4Der would clearly see all the inside points at the same time with all the connections of the points to each other spread out over a flat 3D area. Some how the points that make up the six faces would clearly be seen as the surface of the cube. If we were talking about a sphere the situation is even worse. I want a representation that would clearly show all the surface points drawn on a 3D flat surface with all the connections between the points clearly visible with no overlaps. The surface points of the Sphere would have to clearly be shown to contain the inside points with no overlapping. All points on the surface and inside the Sphere would be spread out over a Flat 3D Hyper Plane from the point of View of the 4Der. He sees inside the Sphere. I still maintain that our Brains will not let us see these things in this way. I hyped it up by observing that if we did have a 4D Brain that we would have 32000 times more neurons and so be 32000 times more intelligent. The added intelligence is good but probably not necessary for understanding 4D Space. However a 3D Retina and 3D Visual Cortex is absolutely necessary. This means that a 4D Cat would understand things about 4D Space that we can not. The understanding would be Visual not theoretical. In this sense a 4D Cat might be smarter than we are. I think we can understand 4D Space the best that 3Ders can do, but we can never understand 4D Space like 4Ders would. I think I should have emphasized the stipulation "Like a 4Der" in my original post.Klitzing wrote:I agree, simply slicing 3D bodies and viewing disconnected slices as some series does not provide a good understanding of 3D by means of simple 2D objects.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
You don't necessarily have to view it as a 4d person ought. It is understanding, rather than physical form that matters.
There has been a fierce debate here on whether the spherical tiling of eight cubes, constitutes a tesseract or not. It has no terrage, and thus is not a 4d figure, but a 3d tiling.
Of course, things like lace cities and various other projections help. With lace cities we have been able to reach eight dimensions. With laminate tilings, twentyfour.
But i digress.
There has been a fierce debate here on whether the spherical tiling of eight cubes, constitutes a tesseract or not. It has no terrage, and thus is not a 4d figure, but a 3d tiling.
Of course, things like lace cities and various other projections help. With lace cities we have been able to reach eight dimensions. With laminate tilings, twentyfour.
But i digress.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Why Humans Will Never Understand 4D Space
By analogy if you circularly tile six squares in 2D Space you can never get a cube. In fact the 2D observer will still have no idea what a cube is by doing this. If you take all the techniques that we use to try to understand 4D Space and apply them to a 2Der trying to understand 3D Space you will see how the 2Der can never really see a cube for what it is. Even more importantly the 2Der will never even understand the flatness of a square in 3D Space.wendy wrote:You don't necessarily have to view it as a 4d person ought. It is understanding, rather than physical form that matters.
There has been a fierce debate here on whether the spherical tiling of eight cubes, constitutes a tesseract or not. It has no terrage, and thus is not a 4d figure, but a 3d tiling.
Of course, things like lace cities and various other projections help. With lace cities we have been able to reach eight dimensions. With laminate tilings, twentyfour.
But i digress.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Another fundamental principle that I cover heavily in my Animations is the behavior of rotational axes. In 2D it is a Point, in 3D it is a Line, and in 4D it is a Plane. So the other thing, besides the 3D Hyper Plane, that I think we (maybe just me) need to concentrate on is how can a Plane rotate in Place? The 2Der will not understand a Line rotating in place. I think if you examine the futility of a 2Der trying to understand this you will understand why we will be unable to understand a Plane rotating in place. We can use all the techniques including the ones I use in my Animations but it will always elude us to fully understand it. We can not get out of our 3D Space prisons. Also, just looking at equations does not do it for me. We need 4D Brains and therefore 3D Retinas and 3D Cortexes.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
The key to constructing a Tesseract is to view the sides not as 8 cubes but as 8 3D Hyper Plane objects. Thinking of the sides as cubes will always prevent proper understanding of the Tesseract. If you view the sides as cubes you will be looking at the 3d Hyper Plane Object from an edge view. You must view the cube from 4D Space where it becomes a Flat 3D Object. This is where the Hyper Plane visualization is so important. Now the cubes look more logically like some kind of side objects since they are Flat in 4D Space. So the Tesseract is really constructed from 8 Flat Hyper Space objects in 4D Space. If the Tesseract is centered at the origin then for each of the 4 axes there will be a Flat 3D Object perpendicular to the axis located at equidistant positions plus and minus of the origin. Since the Flat 3D Objects are flat they would seem to fit together and connect to each other at lines like a regular cube. However this is now 4D Space and the Flat 3D objects fit together to form the Tesseract on 2D edges. Each Flat 3D object will connect with six other Flat 3D objects to form the Tesseract. If there is a test particle randomly floating around inside the Tesseract it will bounce off of 8 different bounding Flat 3D objects that make up the sides of the Tesseract. The point is that when the test particle hits a side it will be only a single point away from the outside since the side is Flat. If you think of the sides as cubes you will always be hitting the sides of cube objects and are one whole cube size distant from the outside. The next thing we can do is unfold the Tesseract into 3D Space by rotating the Flat 3D sides on the 2D Planes that connect them to each other. You should see my original post (Exploring the 4th Dimension Using Animations) to view the animations for a good demonstration of these kinds of constructions and rotations. One last suggestion is to think about what the 2Der has to do with the 6 squares that make up a cube in order to understand the cube. The 2Der would obviously not want to look at the squares on their edges, which is really all he can do from his 2D Space, but rather would need to understand the flatness of a square by somehow seeing it from 3D Space.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Do you really need to have a real 4D perception in order to grasp the local connectivities of 4D polychora?
I would not think so. But there is still something better than just doing sections and then having sequences of unconnected such section pics. The point here is, that the continuity is missing. But even sectioning movies would not give the required for feeling. For then still the overview is lacking.
The Schlegel diagrams on the other hand will help here out quite well. It is the best suited aid I could think of. If done correctly, that is, if the projection center was being chosen close enough atop some specific cell, and if the polychoron to be considered was convex, then everything would project right into that very cell. Thus, if that very cell would be considered in addition to be rather "the outer space" instead, then the whole picture would be fully free of any overlap! - Sure, if only speaking of a mere projection, i.e. when the projection center was not chosen to be close enough, then you might encounter some overlaps instead. But that's then just a matter of a bad choice of the fokus. (Or simply due to the further projection of the 3D Schlegel diagram of the 4D object down to a 2D picture...)
In fact, I would even go a step further. You not even really need to have a full understanding of a gloabal 4D space, in order to grasp 4D polychora. That is just because the polychora locally are made of some 3D fabric only. Therefore you could consider a polychoron just like an ant, running on the surface of a ball. That is, when you can understand 3D honeycombs or according cell complexes in a localized manner, then there would be no much difference whether this cell structure would close in a spherical, in an euclidean, or in a hyperbolic way. And that beyond that local 3D fabric there would be some perpendicular (radial) direction, kind some ana and katha turning towards the polychoral outside resp. polychoral inside, that is rather irrelevant here.
The only point to consider, when mapping such curved surface spaces into our 3D euclidean perception space, is that the respective cells get somewhat distorted to match the according excess. - Else you'd end up with a mere net only, which then has to be folded and reconnected across the gaps. Nets, in fact, whenever the gaps would not be localized at some specific point of current interest, also might serve for some considerations. But then the overall continuity would be lacking, for sure.
Thus, to conclude, there is a good lot of aids in order to visualize many 4D aspects, even without having a true 4D eye and a 3D retina. I.e. it is not that you have to really "see" 4D in order to just understand 4D.
--- rk
I would not think so. But there is still something better than just doing sections and then having sequences of unconnected such section pics. The point here is, that the continuity is missing. But even sectioning movies would not give the required for feeling. For then still the overview is lacking.
The Schlegel diagrams on the other hand will help here out quite well. It is the best suited aid I could think of. If done correctly, that is, if the projection center was being chosen close enough atop some specific cell, and if the polychoron to be considered was convex, then everything would project right into that very cell. Thus, if that very cell would be considered in addition to be rather "the outer space" instead, then the whole picture would be fully free of any overlap! - Sure, if only speaking of a mere projection, i.e. when the projection center was not chosen to be close enough, then you might encounter some overlaps instead. But that's then just a matter of a bad choice of the fokus. (Or simply due to the further projection of the 3D Schlegel diagram of the 4D object down to a 2D picture...)
In fact, I would even go a step further. You not even really need to have a full understanding of a gloabal 4D space, in order to grasp 4D polychora. That is just because the polychora locally are made of some 3D fabric only. Therefore you could consider a polychoron just like an ant, running on the surface of a ball. That is, when you can understand 3D honeycombs or according cell complexes in a localized manner, then there would be no much difference whether this cell structure would close in a spherical, in an euclidean, or in a hyperbolic way. And that beyond that local 3D fabric there would be some perpendicular (radial) direction, kind some ana and katha turning towards the polychoral outside resp. polychoral inside, that is rather irrelevant here.
The only point to consider, when mapping such curved surface spaces into our 3D euclidean perception space, is that the respective cells get somewhat distorted to match the according excess. - Else you'd end up with a mere net only, which then has to be folded and reconnected across the gaps. Nets, in fact, whenever the gaps would not be localized at some specific point of current interest, also might serve for some considerations. But then the overall continuity would be lacking, for sure.
Thus, to conclude, there is a good lot of aids in order to visualize many 4D aspects, even without having a true 4D eye and a 3D retina. I.e. it is not that you have to really "see" 4D in order to just understand 4D.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Why Humans Will Never Understand 4D Space
I think these diagrams show connectivities but completely obscure the real appearance of objects. These diagrams seem to eliminate the insides of the object. I think you need the 4D view even with these diagrams. Take the Tesseract for example. from my 3D perspective the central small cube seems to be completely surrounded by the other warped cubes and completely inside the large outside cube. There is no inside with these diagrams. Also this kind of representation of a Tesseract continues to show the Tesseract as being made out of cubes. While technically true in 3D Space it is not what a 4Der sees. The 4Der sees 8 Flat 3D objects connected together to form the Tesseract. If you put a test particle inside the Tesseract and let it randomly move around it will eventually bounce off of all the walls. At the point of impact on any wall and at any position on the wall the particle will be only one point (the thickness of the wall) away from the outside of the Tesseract. By making the sides look like cubes you would get the impression that the test particle would be hitting the sides of cubes and never hitting any points inside any cube. By making the sides look like cubes the diagram is completely obscuring the reality of a Tesseract. I think the key is in visualizing how things like cubes and spheres are actually Flat in 4D Space and then putting them together.Klitzing wrote:Do you really need to have a real 4D perception in order to grasp the local connectivities of 4D polychora?
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Indeed, it is more the honeycomb view of the mere surface topology. That is, every point of this perception space would be attached at ana side to the inner of the polytope and at katha side to the outer of the polytope. Or putting it in different words: the inner and outer spaces completely are blended out in a mere surface view, for sure.
--- rk
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Why Humans Will Never Understand 4D Space
You know. it took me days to figure out Weimholt's hexahedron, until i made a model of it in zometools.
None the same, you make models and understand from how the models work, what it does in real life. You don't have to hack at twelve inches!
It really isn't a matter of what is in front of the eyes. The art of seeing is also in the brain. With the likes of lace cities or bubblegrams or schlegel diagrams, one can see the surface.
On the other hand, to sit down and consider what a 4d map ought look like, considering the nature of the day and the seasons and the climata, is not something that intuitively flows from three dimensions, nor is the nature of the various rotations in 4d, or the implication of using a non-wheel rotation on a wheeled vehicle. Yet these answers come to me visually. I'm hopeless at things like algebra.
But then again, Schwarzchild's metric was by me solved visually. It's a matter of a slightly distorted common sense.
None the same, you make models and understand from how the models work, what it does in real life. You don't have to hack at twelve inches!
It really isn't a matter of what is in front of the eyes. The art of seeing is also in the brain. With the likes of lace cities or bubblegrams or schlegel diagrams, one can see the surface.
On the other hand, to sit down and consider what a 4d map ought look like, considering the nature of the day and the seasons and the climata, is not something that intuitively flows from three dimensions, nor is the nature of the various rotations in 4d, or the implication of using a non-wheel rotation on a wheeled vehicle. Yet these answers come to me visually. I'm hopeless at things like algebra.
But then again, Schwarzchild's metric was by me solved visually. It's a matter of a slightly distorted common sense.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Why Humans Will Never Understand 4D Space
Seeing a particular viewpoint from a different perpendicular direction indicates the existence of a higher dimension.
A 2D viewpoint of a 1D line "all the way around it" would be possible in 3D space.
A 3D viewpoint of a 2D plane "all the way around it" would be possible in 4D space.
So seeing a 3D viewpoint "all the way around it" would kind of like be experiencing 4D.
It would be in 3D slices at a time, but overall, one could get a sense of the 4D totality of it.
My two cents.
A 2D viewpoint of a 1D line "all the way around it" would be possible in 3D space.
A 3D viewpoint of a 2D plane "all the way around it" would be possible in 4D space.
So seeing a 3D viewpoint "all the way around it" would kind of like be experiencing 4D.
It would be in 3D slices at a time, but overall, one could get a sense of the 4D totality of it.
My two cents.

My VRI channel: http://youtube.com/channel/UCntWMVVl5wKCx_6CH33_mXg
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: Why Humans Will Never Understand 4D Space
To see if I understand what you are saying let's apply this to a 2Der trying to understand a cube. Let's slice up the cube into a bunch of squares and put these squares into the 2Ders 2D Space. He can only see them from their edge views. This deconstruction of the cube gives him no idea how they connect to each other. He sees them as nice solid squares with beautiful width and depth. In order for him to see how they connect he must see them as Flat objects but in his world a square is not a Flat object. it is a solid impenetrable object that he can walk all the way around. He is unable to see the Flatness of these squares. He can know in theory how to do it but he will never really know how to stack them up. The situation is the same for a 3Der looking at a bunch of cube slices of a Tesseract Unless the 3Der recognizes the Flatness of a cube in 4D Space I don't see how looking at 3D cubes gives him a good way to understand 4D Space. I agree it's a start but the missing element is in recognizing the Flatness of 3D objects in 4D Space. When you can see how they are actually Flat they will stack up in a more understandable way. The problem is in seeing the Flatness and I think this is a limitation of our 3D Brains.Hugh wrote:Seeing a particular viewpoint from a different perpendicular direction indicates the existence of a higher dimension.
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
Id like to thank everyone for their comments over the weekend. I want to say a few more things about the Tesseract. It is commonly said that the sides of a Tesseract are made out of cubes. In fact Tesseracts are not made out of 3D cubes like the ones that exist in our 3D Space. The Tesseract cubes have an extra dimension. They are in fact something different than our 3D cubes. They are Flat 3D Objects. If you look at them on edge, in a 4D Space, they will look like 3D cubes. But these cubes have a Flat characteristic that is the main characteristic of a cube in 4D Space. These Flat 3D Objects must be oriented so that their Flat sides form the sides of the Tesseract. They connect to each other at 2D Objects that have a Line like characteristic. Yes 2D Objects in 4D Space have a line like characteristic. Two Tesseract sides connected on these 2D Lines can pivot about each other like they were hinged together. This is why a 2D object can rotate in place like an axis. My Animations show this in some detail. Bottom line of all this is that a Tesseract is a simple box with thin sides in 4D Space. It seems like projections, slices, etc. make them into something more complicated than is needed. I'll have to speak for myself and say that I can not make a Tesseract out of bunch of cubes in 3D Space. Just like the 2Der will never understand a cube by looking at a bunch of squares in his 2D Space. He would have to see the Flatness of a square but he is always looking at the squares on edge. Just in case here is the link to my Animations:
http://www.theintermind.com/ExploringTh ... ations.asp
http://www.theintermind.com/ExploringTh ... ations.asp
- SteveKlinko
- Dionian
- Posts: 31
- Joined: Tue Aug 20, 2013 10:32 pm
- Location: Titusville Florida
Re: Why Humans Will Never Understand 4D Space
SteveKlinko wrote:To see if I understand what you are saying let's apply this to a 2Der trying to understand a cube. Let's slice up the cube into a bunch of squares and put these squares into the 2Ders 2D Space. He can only see them from their edge views. This deconstruction of the cube gives him no idea how they connect to each other. He sees them as nice solid squares with beautiful width and depth. In order for him to see how they connect he must see them as Flat objects but in his world a square is not a Flat object. it is a solid impenetrable object that he can walk all the way around. He is unable to see the Flatness of these squares. He can know in theory how to do it but he will never really know how to stack them up.Hugh wrote:Seeing a particular viewpoint from a different perpendicular direction indicates the existence of a higher dimension.
In order for the 2Der to understand the fullness of 3D, he has to take his 2D slice of 3D and turn it "all the way around" the 1D line that he understands into a "new direction". He understands forward/back and right/left, but just has to understand that there is a new perpendicular direction to each of these that is available. Once he realizes that, he can appreciate that there is an up/down that any of his axes can be re-oriented in, and understand the "new space" that is made available because of it.
SteveKlinko wrote:The situation is the same for a 3Der looking at a bunch of cube slices of a Tesseract Unless the 3Der recognizes the Flatness of a cube in 4D Space I don't see how looking at 3D cubes gives him a good way to understand 4D Space. I agree it's a start but the missing element is in recognizing the Flatness of 3D objects in 4D Space. When you can see how they are actually Flat they will stack up in a more understandable way. The problem is in seeing the Flatness and I think this is a limitation of our 3D Brains.
In order for the 3Der to understand the fullness of 4D, he has to take his 3D slice of 4D and turn it "all the way around" the 2D plane that he understands into a "new direction". He understands forward/back, right/left and up/down, but just has to understand that there is a new perpendicular direction to each of these that is available. Once he realizes that, he can appreciate that there is an ana/kata that any of his axes can be reoriented in, and understand the "new space" that is made available because of it.

My VRI channel: http://youtube.com/channel/UCntWMVVl5wKCx_6CH33_mXg
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: Why Humans Will Never Understand 4D Space
SteveKlinko wrote:To see if I understand what you are saying let's apply this to a 2Der trying to understand a cube. Let's slice up the cube into a bunch of squares and put these squares into the 2Ders 2D Space. He can only see them from their edge views. This deconstruction of the cube gives him no idea how they connect to each other. He sees them as nice solid squares with beautiful width and depth. In order for him to see how they connect he must see them as Flat objects but in his world a square is not a Flat object. it is a solid impenetrable object that he can walk all the way around. He is unable to see the Flatness of these squares. He can know in theory how to do it but he will never really know how to stack them up. The situation is the same for a 3Der looking at a bunch of cube slices of a Tesseract Unless the 3Der recognizes the Flatness of a cube in 4D Space I don't see how looking at 3D cubes gives him a good way to understand 4D Space. I agree it's a start but the missing element is in recognizing the Flatness of 3D objects in 4D Space. When you can see how they are actually Flat they will stack up in a more understandable way. The problem is in seeing the Flatness and I think this is a limitation of our 3D Brains.Hugh wrote:Seeing a particular viewpoint from a different perpendicular direction indicates the existence of a higher dimension.
I'd say that slicing the cube is even worse for understanding the cube by mere square sections: the first and the last square actually are faces of the cube, but all the other sections would lay out the inner part of the cube. It is only their sides which lay out sections in turn of the lacing squares of the cube. And this disconnected lower-dimensional sectioning of the lacing elements is what makes the sectional representation so hard to grasp.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
46 posts
• Page 1 of 2 • 1, 2
Return to Higher Spatial Dimensions
Who is online
Users browsing this forum: No registered users and 59 guests
