I been thinking sbout thr failings of abstract polytopes. in that most of the definitation apper fairly arbitary, in that it looks like an intersection of some distorted set theory, ad ultimatily resting on some notion that a line is made of points.
This is at odds with the notiom that a point in n space requires n equals signs, or partitions of space. It doesn't really handle round things, in so much that it autamaticly supposes flat things the dyadic rule is totally not needed. It is a provable condition if one suppose simgle density.
Thoughts about polytope definitions
14 posts
• Page 1 of 1
Thoughts about polytope definitions
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
The current approach looks at cuts giving \(n-c\) dimensional spaces such as satified by c equal signs This produces a nsked fabric in that we povider a series of *surtopes* to boundthe fabric. this involves "mounting" such that the interior of the surface patch is at the limit of the patch.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
Interpreting abstract polytopes in terms of point sets was the original motivation for abstract theory, but it is quite unnecessary and leads to difficult contradictions. For example to dualise, you just reverse the Hasse diagram. Now try dualising the combinatorics of all those point sets!
It is simplest, most elegant and most powerful to treat each element as a primitive object of dimension or rank k (for -1 < k < n). As Hilbert said in a related context, "we might as well be talking of tables, chairs and beer mugs" as planes, lines and points.
We can then map or "realize" the abstract structure onto whatever kind of "polytope" we choose to define.
It is simplest, most elegant and most powerful to treat each element as a primitive object of dimension or rank k (for -1 < k < n). As Hilbert said in a related context, "we might as well be talking of tables, chairs and beer mugs" as planes, lines and points.
We can then map or "realize" the abstract structure onto whatever kind of "polytope" we choose to define.
- steelpillow
- Trionian
- Posts: 71
- Joined: Sat Jan 15, 2011 7:06 pm
- Location: England
Re: Thoughts about polytope definitions
Happy birthday, Wendy!
I agree with steelpillow here; points and planes are equally fundamental. Where do you find a suggestion that a line or plane is made of points, in the context of abstract polytopes? (I have no problem with the notion in general.)
I agree with steelpillow here; points and planes are equally fundamental. Where do you find a suggestion that a line or plane is made of points, in the context of abstract polytopes? (I have no problem with the notion in general.)
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 561
- Joined: Tue Sep 18, 2018 4:10 am
Re: Thoughts about polytope definitions
That a product might be described as a join or union based on the addition of vertices suggest that polytopes are little more than some hull surrounding a set of vertces. at no point do you see the kind of description that 'for all A, for all B there exists a unique AB, as i descirbe in polytopes.pdf little attention is given to the intermediate surtopes. NWJ reiterates that thes are sums, that somehow a tegum is a count of vertices,
The whole discussion with URL (vi.hndz.p) resolves around that a surtope is a set of points.
The notion of mr_e_man is that one can form a union of sets (a,b,c) and (c,d,e) that include two entries sounds to me to be an unwarranted extention to the theory, as if we must coount 'red' and 'car' as separate entities, and not features applied that apply to any motor car that is red. In my younger i was sketching up how one could unify mathematics, since any object would be a list, the things like 'set' parity' would be functions that reduces the input to just separate distinct objects. And each of these functions have complimentry forms, The set of factors of 120, gives 30 the coset is 4, the lists involve (2, 2, 2, 3, 5) the set is (2,3,5) the coset is (2,2)= factors less set.c coset has also an other meaning, in the a parallel set.
The whole discussion with URL (vi.hndz.p) resolves around that a surtope is a set of points.
The notion of mr_e_man is that one can form a union of sets (a,b,c) and (c,d,e) that include two entries sounds to me to be an unwarranted extention to the theory, as if we must coount 'red' and 'car' as separate entities, and not features applied that apply to any motor car that is red. In my younger i was sketching up how one could unify mathematics, since any object would be a list, the things like 'set' parity' would be functions that reduces the input to just separate distinct objects. And each of these functions have complimentry forms, The set of factors of 120, gives 30 the coset is 4, the lists involve (2, 2, 2, 3, 5) the set is (2,3,5) the coset is (2,2)= factors less set.c coset has also an other meaning, in the a parallel set.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
A surtope is a set of points only if space is a set of points. This is a common dogma, maintained by NWJ among many others. He tried hard to construct abstract polytopes as point sets, and failed. It works only for convex realizations.
If you assume that everything is points, then of course the busiest points - the vertices - will be the most important thing in your vision.
Space can be made of many other things and a polytope may be seen for example as the enclosure of a set of planes, or the meet or intersection of a set of half-spaces. Better to make no such assumptions at all. An abstract polytope is a child of algebraic set theory, it is not geometry. That we can apply it to geometric polytopes is a great beauty and a great enlightenment.
Sets also have symmetries, which become the symmetries of the polytope. Symmetries often involve factors, as seen for example in the idea that {6/2} is a pair of {3} superimposed. Or, if we wind {6} twice, it ends up with the symmetry of {3}. Where we see factors we see a conservation law, and where we see a conservation law, we see a symmetry.
If you assume that everything is points, then of course the busiest points - the vertices - will be the most important thing in your vision.
Space can be made of many other things and a polytope may be seen for example as the enclosure of a set of planes, or the meet or intersection of a set of half-spaces. Better to make no such assumptions at all. An abstract polytope is a child of algebraic set theory, it is not geometry. That we can apply it to geometric polytopes is a great beauty and a great enlightenment.
Sets also have symmetries, which become the symmetries of the polytope. Symmetries often involve factors, as seen for example in the idea that {6/2} is a pair of {3} superimposed. Or, if we wind {6} twice, it ends up with the symmetry of {3}. Where we see factors we see a conservation law, and where we see a conservation law, we see a symmetry.
- steelpillow
- Trionian
- Posts: 71
- Joined: Sat Jan 15, 2011 7:06 pm
- Location: England
Re: Thoughts about polytope definitions
wendy wrote:The notion of mr_e_man is that one can form a union of sets (a,b,c) and (c,d,e) that include two entries
How did that enter the discussion? I didn't think it was important. But I'll try to explain it again.
To make a "disjoint union", you just stick a label on each element to tell which set it came from. Given the two sets {a,b,c} and {c,d,e}, where of course c=c, you construct two new sets consisting of pairs, {(a,1), (b,1), (c,1)} and {(c,2), (d,2), (e,2)}. We have (c,1)≠(c,2) because 1≠2. Ordered pairs are equal only if their corresponding components are equal.
In some sense, it's a way of enforcing 3+3=6 rather than 3+3=5.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 561
- Joined: Tue Sep 18, 2018 4:10 am
Re: Thoughts about polytope definitions
disjoint unionns is an unnecessary step, you get the ssme effect by multiplying each set by a name, ant then take the union. so as you have it c,1 and c,2 are different elements. i t is a weird way to go, and not in the set theory i was taudht.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
the hexagram has order 12 stmmetry, you cant get this from the spool ={6\2}, which has order six symmetry. the extra mirrors exchange the triangles. so symettry does not arise from vertex count.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
The real weakness of abstract polytope theory is also its greatest strength, in its failure to address geometry. We are cleansed of points and windings and things, instead we are left with a set-theoretic structural recipe, a rigorous foundation but no more.
And so we must "realize" the recipe and "inject" (whatever that means) the poset into some containing space, where it magically appears as a geometric polytope. But that realization may prove "unfaithful" (whatever we want that to mean), so we enter the traditional game of monster-barring. In the end, our geometry has gained nothing except the greatest gift of all - freedom from preconceptions.
To help the magic along, I like to break the "realization" spell into two steps.
1. Interpretation. We decide on things like points, lines and planes, and whether lines are ranges of points or points are pencils of lines, and so on. In classic geometry, we interpret the polytope surface as a graph drawn on some topological smooth manifold. It now has some sort of nebulous form, but no measurements. I call this a morphic polytope.
2. Concretization. We pick some metric space and immerse the manifold in it. We may wish to flatten the faces, or make all sides and angles equal, or whatever. We may wish, or find that we are obliged, to twist the manifold up and have some fun, as with the tetrahemihexahedron.
We may choose instead to interpret the n-1 faces as half-spaces in a Grassmannian probability space, concretize the body (maximal element) as a particle-particle scattering amplitude in high-energy particle physics, and call it an amplituhedron. The abstract polytope is still the same.
And so we must "realize" the recipe and "inject" (whatever that means) the poset into some containing space, where it magically appears as a geometric polytope. But that realization may prove "unfaithful" (whatever we want that to mean), so we enter the traditional game of monster-barring. In the end, our geometry has gained nothing except the greatest gift of all - freedom from preconceptions.
To help the magic along, I like to break the "realization" spell into two steps.
1. Interpretation. We decide on things like points, lines and planes, and whether lines are ranges of points or points are pencils of lines, and so on. In classic geometry, we interpret the polytope surface as a graph drawn on some topological smooth manifold. It now has some sort of nebulous form, but no measurements. I call this a morphic polytope.
2. Concretization. We pick some metric space and immerse the manifold in it. We may wish to flatten the faces, or make all sides and angles equal, or whatever. We may wish, or find that we are obliged, to twist the manifold up and have some fun, as with the tetrahemihexahedron.
We may choose instead to interpret the n-1 faces as half-spaces in a Grassmannian probability space, concretize the body (maximal element) as a particle-particle scattering amplitude in high-energy particle physics, and call it an amplituhedron. The abstract polytope is still the same.
- steelpillow
- Trionian
- Posts: 71
- Joined: Sat Jan 15, 2011 7:06 pm
- Location: England
Re: Thoughts about polytope definitions
wendy wrote:disjoint unionns is an unnecessary step, you get the ssme effect by multiplying each set by a name, ant then take the union. so as you have it c,1 and c,2 are different elements.
Exactly. The disjoint union is not an extension to set theory; it can be defined in terms of the existing set theory (the ordinary union and ordered pairs or the Cartesian product). It doesn't necessarily replace the ordinary union. They have different uses.
The union would not be appropriate to describe the construction pictured here. A and B are abstract polytopes, and we don't know what their elements are; we only know how many elements are in a polytope, and the incidence relations between them. So we can't tell whether some element of A is equal to some element of B. That means we don't know how many elements are in the union. But we do know how many elements are in the disjoint union.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 561
- Joined: Tue Sep 18, 2018 4:10 am
Re: Thoughts about polytope definitions
wendy wrote:That a product might be described as a join or union based on the addition of vertices suggest that polytopes are little more than some hull surrounding a set of vertces. at no point do you see the kind of description that 'for all A, for all B there exists a unique AB, as i descirbe in polytopes.pdf little attention is given to the intermediate surtopes.
We can describe the tegum product C of two abstract polytopes A and B, without giving special attention to the vertices.
Omitting the bodies of the polytopes (the greatest elements in the posets), it is just C=A×B (the Cartesian product). For each element a in A, for each element b in B, there is a unique element (a,b) in C. The rank (or "dimension") of (a,b) is the sum of ranks of a and b, plus 1. We can compare two elements (a,b) and (c,d) in C, considering rank and incidence: (a,b) ≤ (c,d) when both a ≤ c and b ≤ d.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 561
- Joined: Tue Sep 18, 2018 4:10 am
Re: Thoughts about polytope definitions
The nullitope does not equate to an empty set. It is actually the namon, and every surtope that is incindent on it is part of that name. If two tringles are placed over each oter each has it on namon, when you turn it into a hexagram, the namons merge. this is true in the tegum product.
dince the products require f(ab)=f(a)f(b) for this to hold the polytopes under draught product require the namon to be at 0 rank, the surtope count is then the product of the equation, baseo at vertex= rank1. In the proguct of repeation the vertex is at rank0.
note that johnson descibed te surtope verge as a polytope cluster(to much like monty python , anthrax cluster)
the verge is that adjacent to a road, inclus the formation as built up to allow drainage. the verge lies in the open lace cone that extends as far as needed like a tetrahedron can be formed by the intesection of v and /\planes. the actua polytope comes from the interior intersection of verge. here the surtope function as the namon.
dince the products require f(ab)=f(a)f(b) for this to hold the polytopes under draught product require the namon to be at 0 rank, the surtope count is then the product of the equation, baseo at vertex= rank1. In the proguct of repeation the vertex is at rank0.
note that johnson descibed te surtope verge as a polytope cluster(to much like monty python , anthrax cluster)
the verge is that adjacent to a road, inclus the formation as built up to allow drainage. the verge lies in the open lace cone that extends as far as needed like a tetrahedron can be formed by the intesection of v and /\planes. the actua polytope comes from the interior intersection of verge. here the surtope function as the namon.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Thoughts about polytope definitions
wendy wrote:The nullitope does not equate to an empty set.
Indeed. It was supposed to originally, but the abstract set theory is much cleaner if it is just another element. Point-set enthusiasts can still realize it as the empty set if it pleases them. But they should remember that while every set contains the empty set, that does not mean that it is a member of every set.
I call the abstract element the nullity. its realization as a polytope is the nullon.
In order to match rank numbering to dimension, it is conventional to rank it –1, with vertices ranked 0. But these numbers are arbitrary, they affect only the detailed form of the equations. It is sufficient merely to specify the order of ranking. It is only when we realize the poset as an object in n dimensions, perhaps a geometric polytope, that the ranking numbers start to matter. For example, depending on which end of the ordering we start counting, we will obtain either one of a dual pair of polytopes.
So I regard an abstract polytope as embodying the structure of both a given geometric form or graph, and the dual form.
If two tringles are placed over each oter each has it on namon, when you turn it into a hexagram, the namons merge.
Topologically I see the hexagram as a surface with two boundaries, like a short tube. Here are my Hasse diagrams of the double-wound hexagon and hexagram:
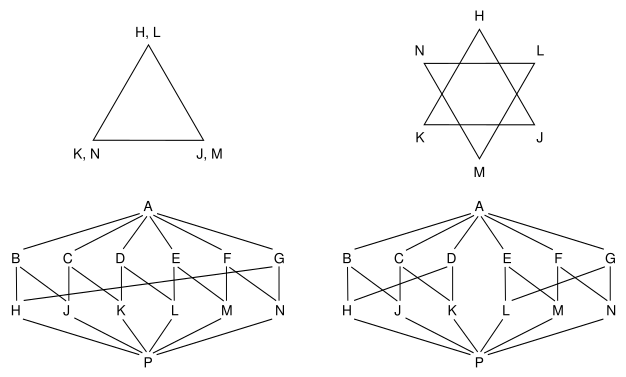
- steelpillow
- Trionian
- Posts: 71
- Joined: Sat Jan 15, 2011 7:06 pm
- Location: England
14 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 54 guests
