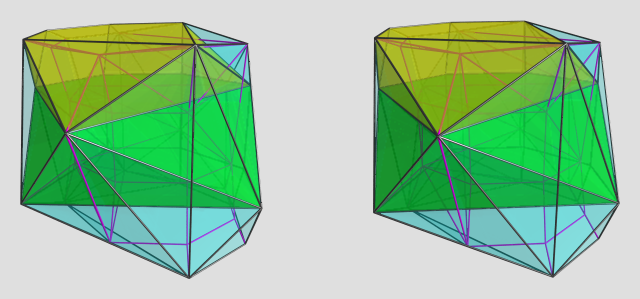
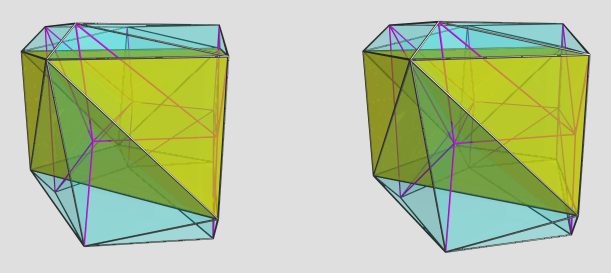
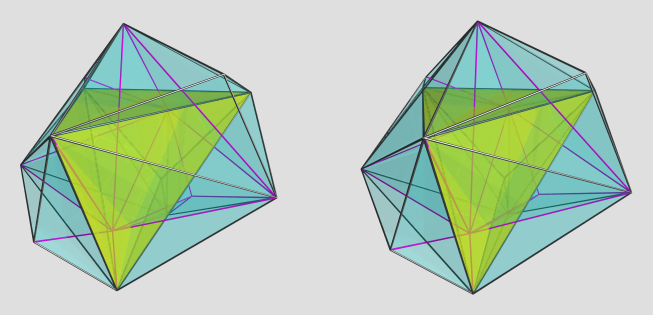
Back on the topic of polychoron symmetry groups...
The simplest type of group without simple rotations would be generated by a single isoclinic rotation (θ, θ), where θ = 360°/m for some fixed integer m. The whole group contains m elements, of the form (nθ, nθ) for various integers n. The transformation matrices look like
- Code: Select all
⌈ cos(nθ) -sin(nθ) 0 0 ⌉
| sin(nθ) cos(nθ) 0 0 |
| 0 0 cos(nθ) -sin(nθ) |
⌊ 0 0 sin(nθ) cos(nθ) ⌋
= cos(nθ)1
M - sin(nθ)K
L.
So, take some random points (x,y,z,w) (say, 2 to 5 points), apply each of these m matrices to each of those points (to get a total of 2*m to 5*m points, of the form (x cos(nθ) - y sin(nθ), x sin(nθ) + y cos(nθ), z cos(nθ) - w sin(nθ), z sin(nθ) + w cos(nθ)), then take the convex hull, and render!

The result will probably look like a tangled blob of tetrahedra. Perhaps we should take the dual, so that the cells have more distinctive shapes, and only 4 cells meet at each vertex.
Now let's look at the more interesting 4D groups, which come from 3D rotation groups. There are 2 infinite families: One type of group has m rotations around a single axis; but that just gives us 2m isoclinic rotations generated by a single isoclinic rotation, which we've already seen. The other type of group has m rotations around one axis, and m 180° rotations around perpendicular axes, as the rotational symmetries of an m-gon prism. Let θ = 360°/(2m). The quaternions representing these rotations have the form
cos(nθ) + k sin(nθ) ,
j cos(nθ) - i sin(nθ) ,
for various integers n. This gives us two types of matrix
- Code: Select all
⌈ cos(nθ) -sin(nθ) 0 0 ⌉ ⌈ 0 0 -cos(nθ) -sin(nθ) ⌉
| sin(nθ) cos(nθ) 0 0 | | 0 0 -sin(nθ) cos(nθ) |
| 0 0 cos(nθ) -sin(nθ) | | cos(nθ) sin(nθ) 0 0 |
⌊ 0 0 sin(nθ) cos(nθ) ⌋ , ⌊ sin(nθ) -cos(nθ) 0 0 ⌋
in the m-gonal prismatic swirl group. (There may appear to be some inconsistent signs (±), but it doesn't matter because n may be replaced with -n.)
In a linked post, I've shown the cube's symmetries and the corresponding multivectors, which can instead be written as quaternions, and then re-interpreted as matrices, which will form the cubic swirl group:
±1,
±i , ±j , ±k ,
(±1 ± i ± j ± k)/2 ,
(±1 ± i)/√2 , (±1 ± j)/√2 , (±1 ± k)/√2 ,
(±i ± j)/√2 , (±i ± k)/√2 , (±j ± k)/√2 .
(All combinations of signs are taken.) For tetrahedral symmetry, simply omit the ones with √2. I'll show just a few of the resulting matrices:
(1 + i + j + k)/2 , (1 + i - j + k)/2 , (1 + k)/√2
- Code: Select all
⌈ 1/2 1/2 -1/2 1/2⌉ ⌈ 1/2 1/2 1/2 1/2⌉ ⌈ 1/√2 1/√2 0 0 ⌉
|-1/2 1/2 1/2 1/2| |-1/2 1/2 1/2 -1/2| |-1/√2 1/√2 0 0 |
| 1/2 -1/2 1/2 1/2| |-1/2 -1/2 1/2 1/2| | 0 0 1/√2 1/√2|
⌊-1/2 -1/2 -1/2 1/2⌋ , ⌊-1/2 1/2 -1/2 1/2⌋ , ⌊ 0 0 -1/√2 1/√2⌋
In fact the tetrahedral swirl group is generated by the first two of these matrices, and the cubic swirl group is generated by the third and either one of the first two.
The dodecahedron's rotational symmetries are represented by the quaternions
±1 ,
±i , ±j , ±k ,
(±1 ± i ± j ± k)/2 ,
(±φ ± φ⁻¹i ± j)/2 , (±φ ± φ⁻¹j ± k)/2 , (±φ ± φ⁻¹k ± i)/2 ,
(±φ⁻¹ ± i ± φj)/2 , (±φ⁻¹ ± j ± φk)/2 , (±φ⁻¹ ± k ± φi)/2 ,
(±1 ± φi ± φ⁻¹j)/2 , (±1 ± φj ± φ⁻¹k)/2 , (±1 ± φk ± φ⁻¹i)/2 ,
(±φi ± j ± φ⁻¹k)/2 , (±φj ± k ± φ⁻¹i)/2 , (±φk ± i ± φ⁻¹j)/2 .
Converting a few of these to matrices:
(1 + i + j + k)/2 , (1 + i - j + k)/2 , (φ + φ⁻¹k + i)/2
- Code: Select all
⌈ 1/2 1/2 -1/2 1/2⌉ ⌈ 1/2 1/2 1/2 1/2⌉ ⌈ φ/2 φ⁻¹/2 0 1/2 ⌉
|-1/2 1/2 1/2 1/2| |-1/2 1/2 1/2 -1/2| |-φ⁻¹/2 φ/2 1/2 0 |
| 1/2 -1/2 1/2 1/2| |-1/2 -1/2 1/2 1/2| | 0 -1/2 φ/2 φ⁻¹/2|
⌊-1/2 -1/2 -1/2 1/2⌋ , ⌊-1/2 1/2 -1/2 1/2⌋ , ⌊-1/2 0 -φ⁻¹/2 φ/2 ⌋
Again the tetrahedral swirl group is generated by the first two, and the dodecahedral swirl group is generated by the third and either one of the first two.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩


 The result will probably look like a tangled blob of tetrahedra. Perhaps we should take the dual, so that the cells have more distinctive shapes, and only 4 cells meet at each vertex.
The result will probably look like a tangled blob of tetrahedra. Perhaps we should take the dual, so that the cells have more distinctive shapes, and only 4 cells meet at each vertex.

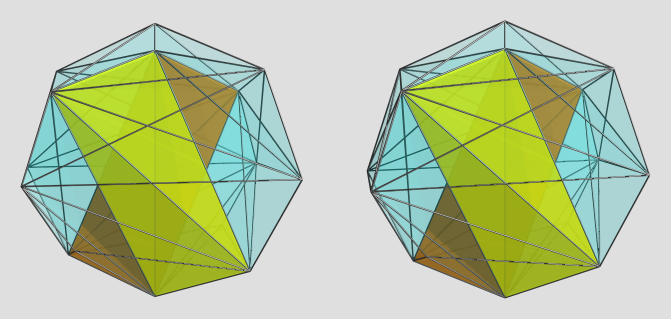
 Just gimme a few minutes to run it through and figure out a nice viewpoint for the dual...
Just gimme a few minutes to run it through and figure out a nice viewpoint for the dual...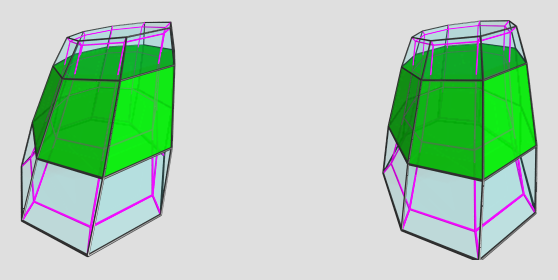

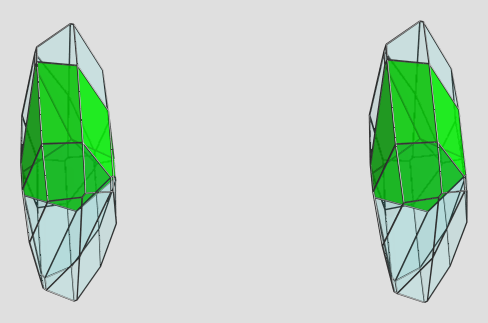
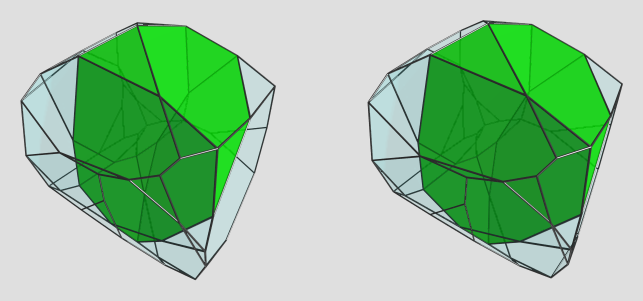
 This is wrong, as shown by (45°, 135°).
This is wrong, as shown by (45°, 135°). They look like what I had in mind.
They look like what I had in mind.