We all know what rays and lines are. Rays go forever in one direction, and lines extend in two.
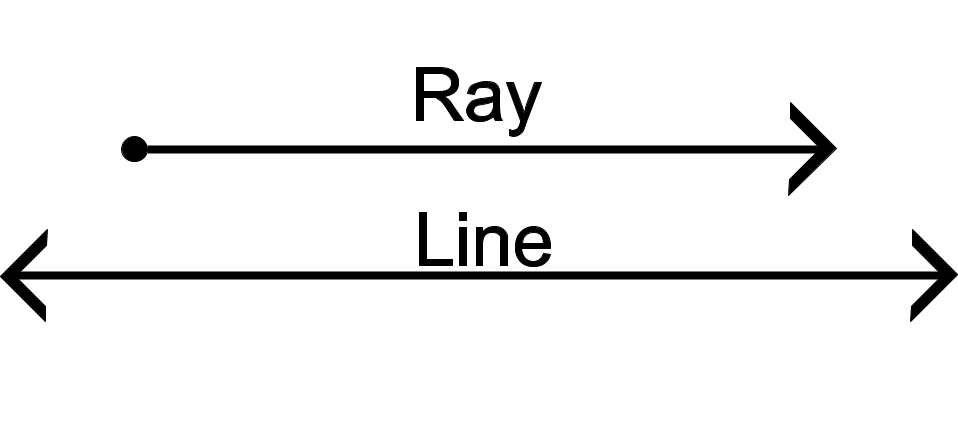
Here, the arrows will mean that the polytope extends to infinity, as this will make things easier to understand.
The question I was wondering was... what would this look like in higher dimensions?
Introducing... the polycara! I'm going to define an n-dimensional polycaron as any shape that has an infinite n-hypervolume.
So what do these look like? I've coined another name for the 2-dimensional polycara: the polycra. I've also put these into 5 general categories, each with a 'professional' and 'unprofessional' name. Without further ado, let's see what they are!
The Planaray (professional: radic prism)

The main idea of this shape is the prism of a ray, or the cartesian product of a line segment and a ray. This specific planaray is what I call a right planaray, because it has two right angles. It is also technically a triangle (3 sides), but only has 2 actual angles.
We can also define many other things with the rays leaving at different angles or having a different polygon at the finite section, and that is the entire category of planarays. Here is an example of one of these irregular planarays:

The Linon (professional: linear prism)

This is similar to the planaray, but with a line. The specific kind of linon you see above is what I will call a regular linon, because it actually is regular. The regular linon can also be defined as the cartesian product of a line segment and a line. The other irregular kinds of linons are just alterations to the intersection of the sides, and adding more sides. Here is an example:

The Angleon (professional: solid angle)

For the most part, this category of shapes takes an angle and turns it into a solid shape. There are 3 basic subcategories of linons:
- Right linon: Has a right angle. This is also the Cartesian product of two rays.
- Regular linon: Has any angle between 0 and 360 degrees.
- Irregular linon: Has additional sides to a regular linon.
The Hemiplane (professional: also hemiplane)

As you may expect, the hemiplane is half of a plane. You can also have irregular hemiplanes by adding sides.
The Plane (professional: Plane)
I don't need an image for this, do I? We all know what the plane is, and it is the Cartesian product of two lines. This is the final category of polycra.
Higher-dimensional polycara
We can get all the other N-dimensional polycara categories by taking the Cartesian products of N line segments, rays, or lines (where there has to be at least 1 ray or line). Because of this, there will be 3N-1 N-dimensional polycara.
Does anybody have any similar ideas or subcategories of these polycara, or possibly some renders of polycara? I find these extremely interesting.
