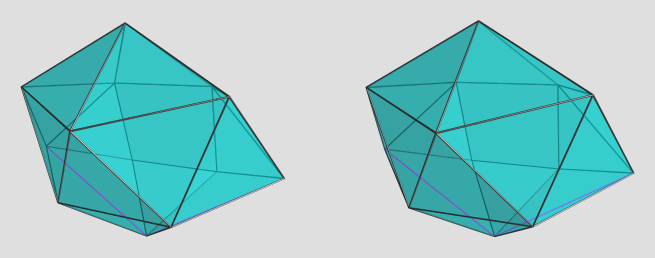
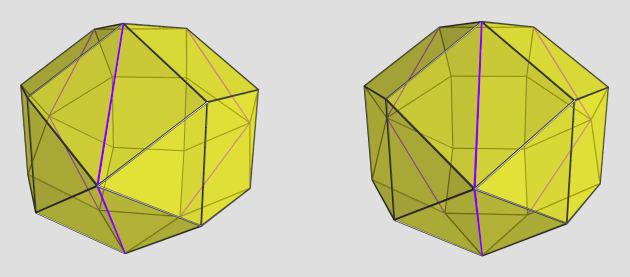
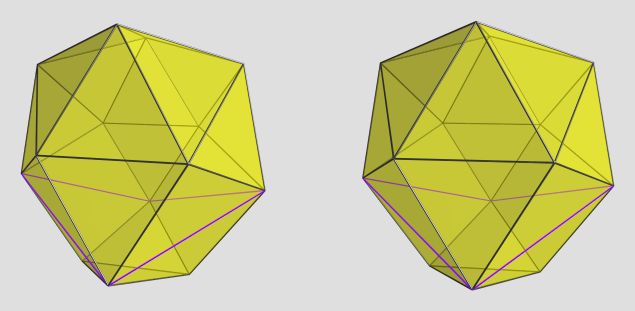
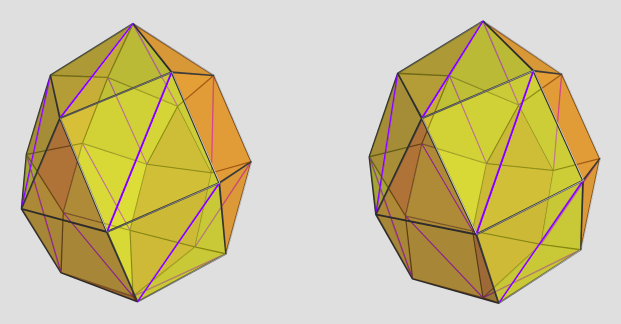
So yesterday I threw together a simple ball-n-springs simulator, and with some tweaks, I could solve many of the polyhedra posted here numerically, and with fairly good accuracy too. And it runs very fast, compared to the polynomial solver.
However, I soon ran into a wrinkle: some of the polyhedra have dependencies between coordinates, e.g., <0, A, B> and <-A, 0, B>, which a simple ball-n-springs model does not express. In order to remedy this, I introduced the idea of a Bar, which behaves sort of like an equalizer between two coordinates of two different balls. It always applies force proportional to the average of two bound coordinates such that it tries to center them on the origin. It's a simplistic hack, but with some care, it does work; I could successfully solve for things like sphenohexocingulum and so forth, with good accuracy and very fast speed (compared to the hours it took to solve it algebraically

). Here, however, I began to run into some of the limitations I mentioned about numerical solvers: in certain systems that depends too much on Bars, the solution converges very slowly -- sublinearly, probably even sublogarithmically. Generally, springs cause fast convergence, but Bars cause slow convergence (unless they're complemented by springs). So Bars are really only useful for maintaining the relationship between +X and -X (to prevent lopsided "solutions" -- local minima in which their absolute values no longer correspond).
Anyway, after getting it to solve bimegalunamegacingulum (aka tetrafolium), I finally felt confident enough to attempt hexonalunamegacorona... only to run into the most feared problem in ball-n-spring simulators: convergence to the wrong solution among multiple local minima. I'm still not 100% sure this is an inherent problem -- in the process I
did discover a mistake in one of the constraints, so it's possible the problem is caused by an error in another constraint -- but it appears to be converging on numerous non-convex solutions, and is very hard to control which solution it converges to. It's highly sensitive to initial conditions and also spring strength: having too high of a spring strength causes convex/concave oscillations in the early iterations that throws off the solution path, but having too low a spring strength slows down convergence significantly. Once the right spring strength has been found, it seems to be highly sensitive to the initial ball positions; a small shift can dramatically change the solution path and lead to very different solutions (all of which, so far, appear to have concavities in one place or another, and it's very hard to control where it will go). There are also many initial conditions that cause the system to diverge altogether.
So right now, I'm stuck trying to find the right initial conditions that will yield the desired solution. And also wondering if I should review the constraints yet again to make sure I didn't screw up the formulation of the system!

There's also the ever-present threat that perhaps this high sensitivity to initial conditions is a sign that there's
no convex solution after all.




 (Either that, or upgrade my PC to have more RAM and hope for the best.
(Either that, or upgrade my PC to have more RAM and hope for the best.  )
)






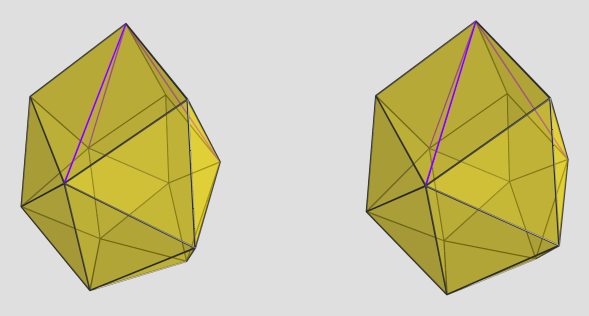
 And so, here it is, the beast itself:
And so, here it is, the beast itself: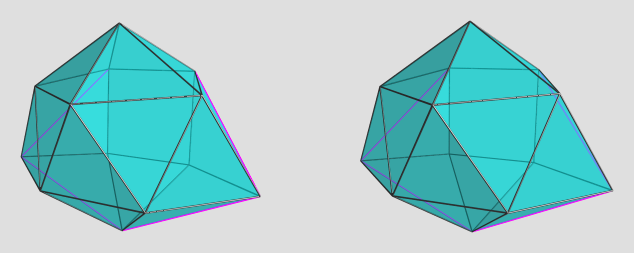
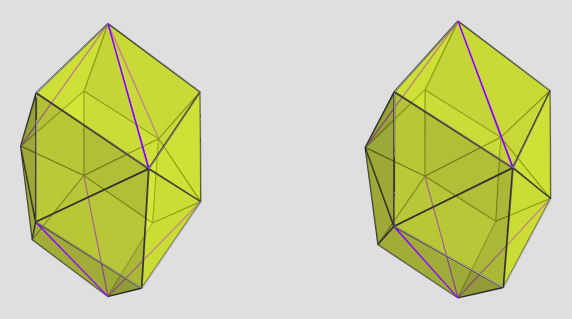
 So here they are:
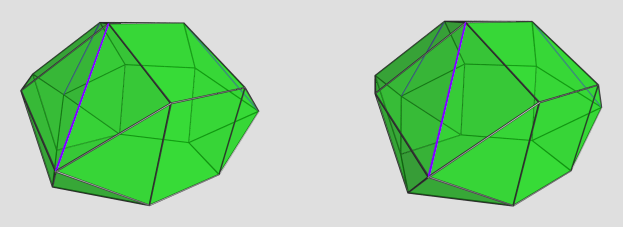
So here they are: But it's just a teeny bit off, so we can't.
But it's just a teeny bit off, so we can't.