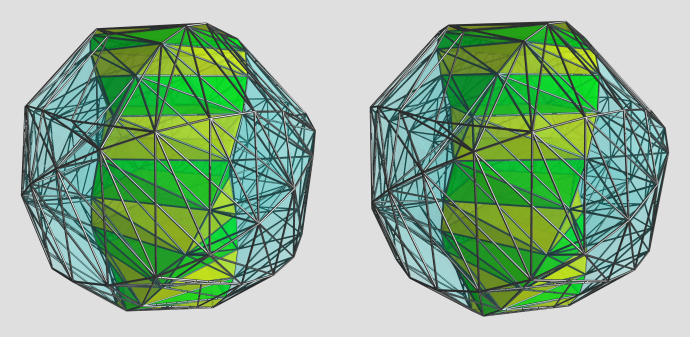
quickfur wrote:Mercurial, the Spectre wrote:[...]
How about the alternated truncated octahedral prism (aka the pyritohedral icosahedral antiprism)? It's not uniform. Coordinates are:
(0, ±1/2, ±0.80901699437494742410, 0.35355339059327376220) (all even permutations for the first three coordinates, for a total of 12 vertices)
(±1/2, 0, ±0.80901699437494742410, -0.35355339059327376220) (same as above for the first three coordinates)
And also its dual.
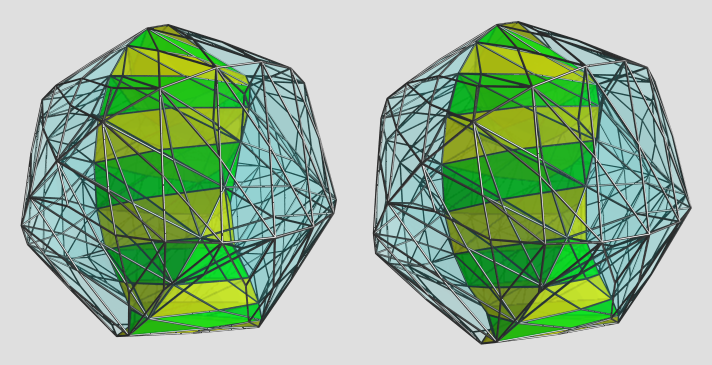
Here's the same projection in a different orientation:
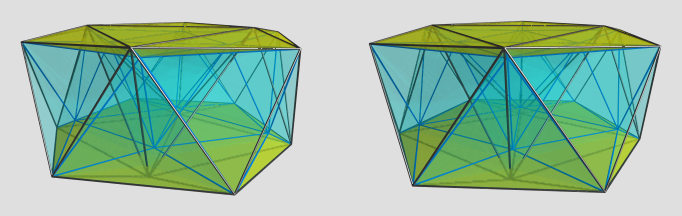
I'm not sure what to make of this; it looks like the prism of an irregular hexagonal prism. Is there a specific 4D viewpoint you have in mind?
Anyway, here's the dual:
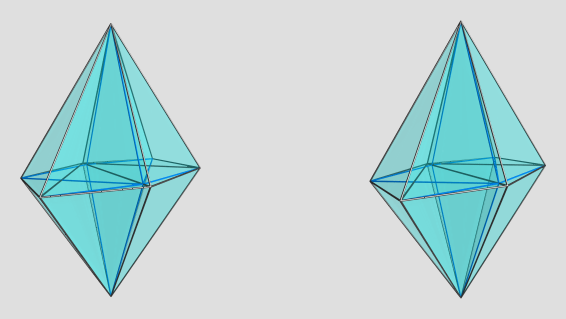
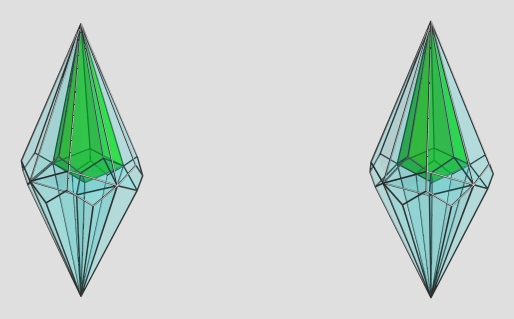
Not sure what to make of this either. It does look like a pretty little diamond shape, though.
Again, if you have a specific 4D viewpoint in mind, do let me know.
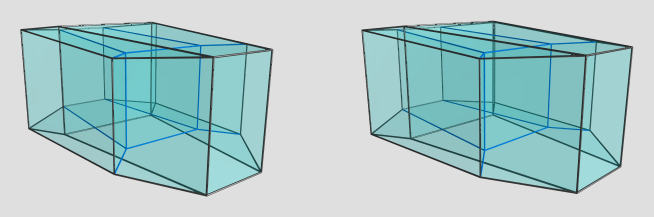
Wait, that's not the shape I had in mind. This shape is actually a distorted 4-6 duoprism and its dual, a 4-6 duopyramid. Sorry.
The coordinates of the alternated truncated octahedral prism are:
(0, ±1/2, ±0.80901699437494742410, 0.35355339059327376220) (4)
(±0.80901699437494742410, 0, ±1/2, 0.35355339059327376220) (4)
(±1/2, ±0.80901699437494742410, 0, 0.35355339059327376220) (4)
They define a regular icosahedron (alternated truncated octahedron) of length 1.
(±1/2, 0, ±0.80901699437494742410, -0.35355339059327376220) (4)
(±0.80901699437494742410, ±1/2, 0, -0.35355339059327376220) (4)
(0, ±0.80901699437494742410, ±1/2, -0.35355339059327376220) (4)
They define another regular icosahedron (alternated truncated octahedron) of length 1, this time antialigned like how a compound of two icosahedra would result in a nonuniform truncated octahedron.





 , so here's an icosahedron-first projection:
, so here's an icosahedron-first projection: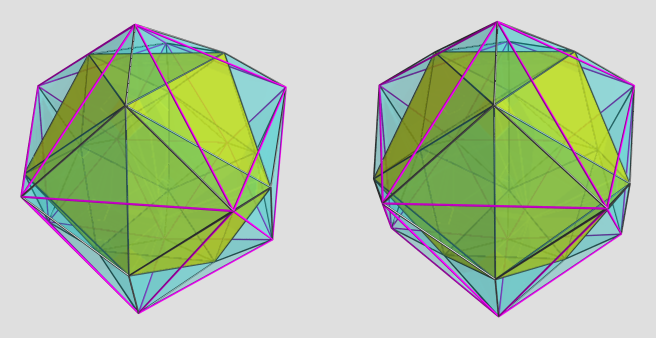
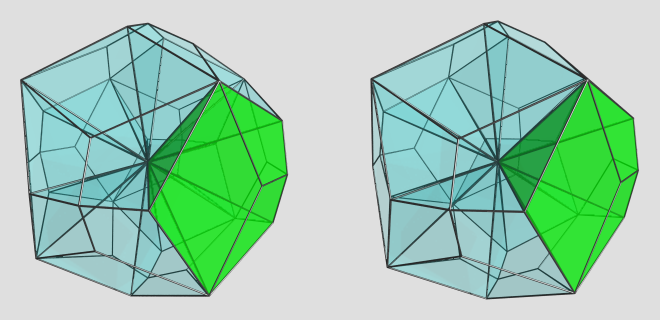
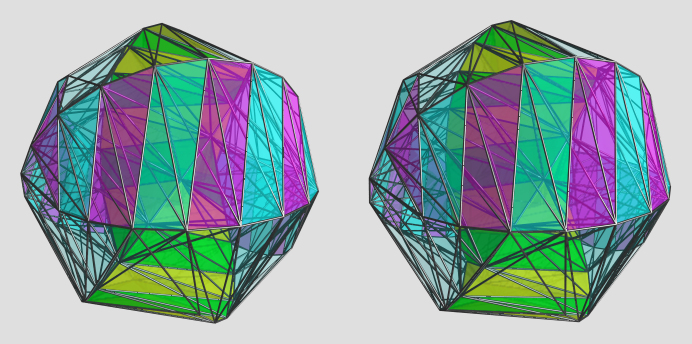
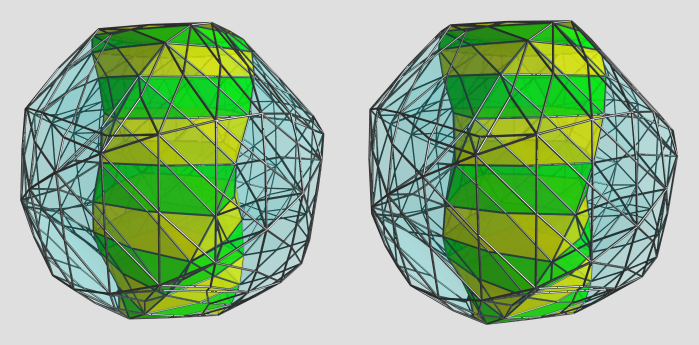

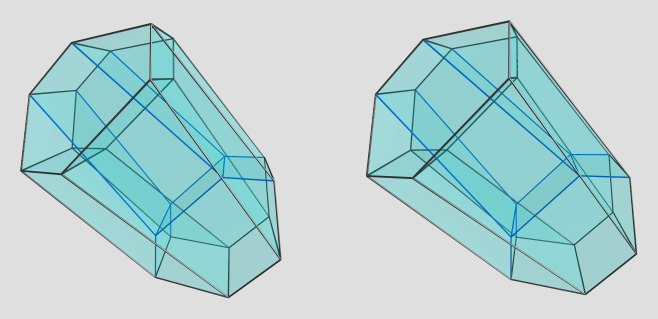
 That generated the desired polytope definition. And now the render:
That generated the desired polytope definition. And now the render: