Isogonal swirl polychora
47 posts
• Page 1 of 2 • 1, 2
Isogonal swirl polychora
I think Bowers has discovered many dice that are very interesting to look at, but unfortunately I don't have access to Stella4D, polyview, or any other 4D rendering software to check with. Unfortunately from what I can find, Stella4D is not free and polyview is not available in Windows.
I have heard of examples such as the 72 square antiprism dice and the 250 sided corkscrew dice. Sounds like their duals are isogonal as well, although I have no idea of the 4D coordinates or any images related to these shapes. But fortunately he mentioned the 16-celled tetrahedral swirl dice which has D3 symmetric cells.
So far I only use GeoGebra to make 3D orthogonal projections of 4D objects. It takes a lot of time to put the vertices and edges. It took me a week to make an F4-centered projection of the omnisnub 24-cell (basically two different 24-gonal projections). For the coordinate transforms I use Wolfram Alpha.
Would you help me join the hunt for these elusive isogonal polychora?
PS. Came back because I forgot to visit this site, just going back to regular isogonal polychoron hunting. I know many of you have searched for CRFs, but why not take a look into the world of isogonal nonuniform polychora? Like the alternated biomnitruncatodecachoron formed as an alternated biomnitruncatodecahoron (convex hull of two omnitruncated 5-cells with two kinds of truncated octahedra) I added in wikipedia.
I have heard of examples such as the 72 square antiprism dice and the 250 sided corkscrew dice. Sounds like their duals are isogonal as well, although I have no idea of the 4D coordinates or any images related to these shapes. But fortunately he mentioned the 16-celled tetrahedral swirl dice which has D3 symmetric cells.
So far I only use GeoGebra to make 3D orthogonal projections of 4D objects. It takes a lot of time to put the vertices and edges. It took me a week to make an F4-centered projection of the omnisnub 24-cell (basically two different 24-gonal projections). For the coordinate transforms I use Wolfram Alpha.
Would you help me join the hunt for these elusive isogonal polychora?
PS. Came back because I forgot to visit this site, just going back to regular isogonal polychoron hunting. I know many of you have searched for CRFs, but why not take a look into the world of isogonal nonuniform polychora? Like the alternated biomnitruncatodecachoron formed as an alternated biomnitruncatodecahoron (convex hull of two omnitruncated 5-cells with two kinds of truncated octahedra) I added in wikipedia.
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Isogonal swirl polychora
I've also been interested in plain old isogonal polytopes (which I just like to call isoforms (semiscaliform also works but the scali part gets cancelled out by semi so it just means "form" and there is an alternative definition where every face just looks like a semiuniform polygon)), especially semiuniforms (uniforms but without the silly restriction of having to have all edges be the same length) which only have documentation for a few examples. I don't really know how to find isogonal polychora nor CRFs however except maybe for faceting vertex figures.
gwa
discord is spiritbackup#1797
discord is spiritbackup#1797
-

ubersketch - Trionian
- Posts: 159
- Joined: Thu Nov 30, 2017 12:00 am
Re: Isogonal swirl polychora
ubersketch wrote:I've also been interested in plain old isogonal polytopes (which I just like to call isoforms (semiscaliform also works but the scali part gets cancelled out by semi so it just means "form" and there is an alternative definition where every face just looks like a semiuniform polygon)), especially semiuniforms (uniforms but without the silly restriction of having to have all edges be the same length) which only have documentation for a few examples. I don't really know how to find isogonal polychora nor CRFs however except maybe for faceting vertex figures.
Stella 4D does great but only rich people have it.......
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Isogonal swirl polychora
I am rich, and I can confirm Stella4d is pretty good but is missing features I would rather have.
gwa
discord is spiritbackup#1797
discord is spiritbackup#1797
-

ubersketch - Trionian
- Posts: 159
- Joined: Thu Nov 30, 2017 12:00 am
Re: Isogonal swirl polychora
If you can compute coordinates for 4D objects you're interested in (convex only, unfortunately), I can make polyview models for them and render them.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:If you can compute coordinates for 4D objects you're interested in (convex only, unfortunately), I can make polyview models for them and render them.
Let me try with the 7-2 step prism, as that can be derived from the 7-7 duoprism:
((0, 1.152382435481243, 1.123489801858734, -0.256429215818139)
(1.123489801858734, -0.256429215818139, 0.5, -1.038260698286168)
(-0.5, -1.038260698286168, -0.5, -1.038260698286168)
(-0.900968867902419, 0.718498696363685, -1.123489801858734, -0.256429215818139)
(0.900968867902419, 0.718498696363685, -0.900968867902419, 0.718498696363685)
(0.5, -1.038260698286168, 0, 1.152382435481243)
(-1.123489801858734, -0.256429215818139, 0.900968867902419, 0.718498696363685)
Can you please identify also the cells (as well as its dual and its cells)?
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Isogonal swirl polychora
Hmm. This is a tough one. It looks like it has 14 (irregular) tetrahedral cells, all joining at rather sharp angles, which makes it really hard to find a good 4D viewpoint. I spent about 20 mins trying to find a good viewpoint, but couldn't.
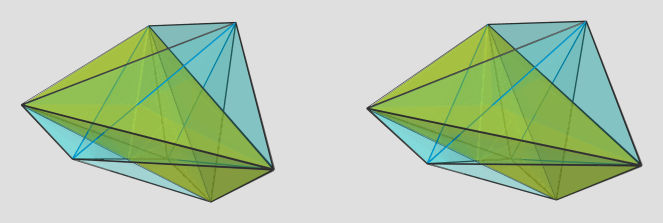
This is the best image I could get after ~20 min's of trying. The yellow cell is the one facing the 4D viewpoint. The faint blue edges lie on the far side of the polytope. There are 4 other cells that lie on this side of the polytope, the rest lie on the far side.
According to the edge length classifier, there are 3 kinds of edges, with lengths approx 2.06, 2.46, and 2.88, respectively. As far as I can tell, all cells are congruent, with all 3 kinds of edges (1 edge of length 2.88, 2 edges of length 2.06, 3 edges of length 2.46). For every cell, there are 2 others that do not share any edges with it (i.e., they only touch at the vertices). Every cell shares at least 1 vertex with every other cell.
If you're interested in step prisms, probably the best bet would be to start with a larger duoprism, so the the result would have blunter angles, as that tends to be easier to visualize via projections.
P.S. It occurred to me that it might be useful to do a vertex-centered projection, so here's one:
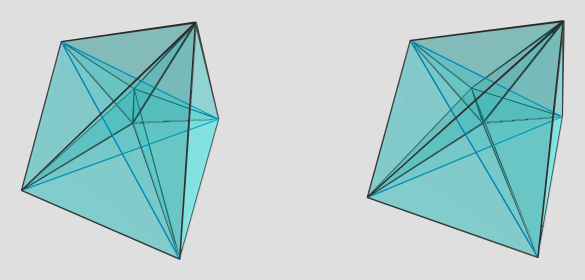
Again, the faint blue edges are on the far side of the polytope. This viewpoint isn't that clear either, but at least if you focus on the edges emanating from the central vertex (the vertex the projection is centered on), you can sort of see the tetrahedral cells folded around it. It's not very clear, though. As I said, it has very sharp angles and so it's hard to get a good viewpoint on it.
As for the dual, let me get to that.

This is the best image I could get after ~20 min's of trying. The yellow cell is the one facing the 4D viewpoint. The faint blue edges lie on the far side of the polytope. There are 4 other cells that lie on this side of the polytope, the rest lie on the far side.
According to the edge length classifier, there are 3 kinds of edges, with lengths approx 2.06, 2.46, and 2.88, respectively. As far as I can tell, all cells are congruent, with all 3 kinds of edges (1 edge of length 2.88, 2 edges of length 2.06, 3 edges of length 2.46). For every cell, there are 2 others that do not share any edges with it (i.e., they only touch at the vertices). Every cell shares at least 1 vertex with every other cell.
If you're interested in step prisms, probably the best bet would be to start with a larger duoprism, so the the result would have blunter angles, as that tends to be easier to visualize via projections.
P.S. It occurred to me that it might be useful to do a vertex-centered projection, so here's one:

Again, the faint blue edges are on the far side of the polytope. This viewpoint isn't that clear either, but at least if you focus on the edges emanating from the central vertex (the vertex the projection is centered on), you can sort of see the tetrahedral cells folded around it. It's not very clear, though. As I said, it has very sharp angles and so it's hard to get a good viewpoint on it.
As for the dual, let me get to that.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
Mmmm, the dual 7-2 step prism is much more interesting, because it has non-tetrahedral cells.  It's still not so easy to get a good view of it, but I managed to find a serviceable viewpoint:
It's still not so easy to get a good view of it, but I managed to find a serviceable viewpoint:
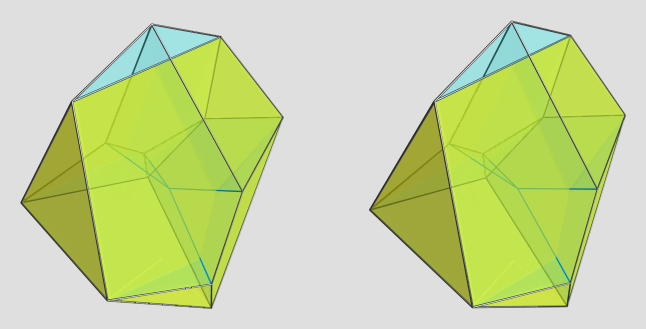
This is a cell-centered projection, with the yellow cell being the one directly facing the 4D viewpoint (i.e., 90° to the 4D viewpoint). It appears to have 2 triangular faces, 2 tetragons, and 2 pentagons, all irregular. There are two other cells that lie on the near side from this viewpoint, each touching the yellow cell on a pentagonal face, and sharing a triangle with each other (seen at the top of the image).
As usual, the blue edges lie on the far side. As far as I can tell, there are only 4 of these, meeting at the antipodal vertex. This particular viewpoint is rather nice in that you can trace the shapes of the remaining cells with not too much difficulty by tracing the edge outlines.
Here's one of the other cells on the near side:
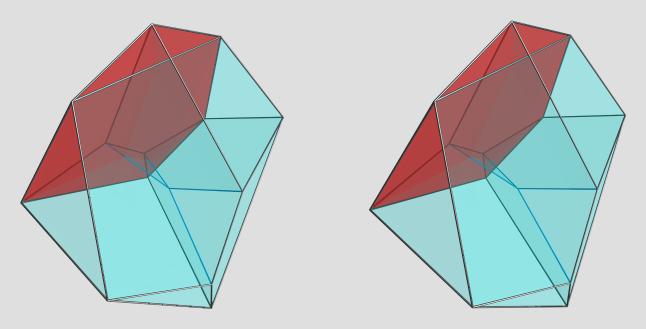
Here's the other one:
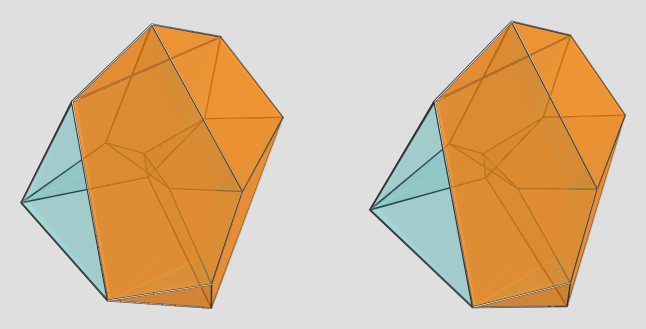
Here are the 4 cells on the far side of the polytope:
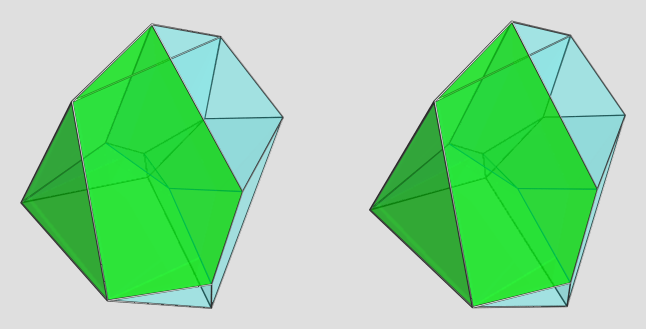
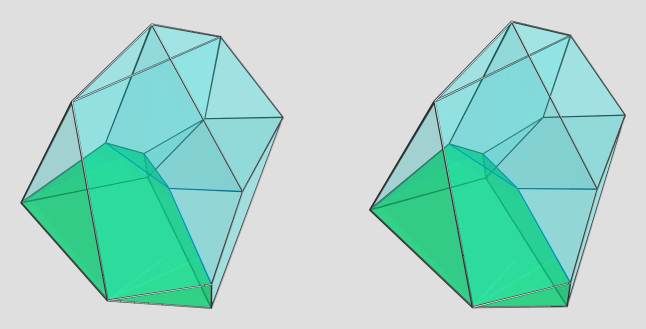
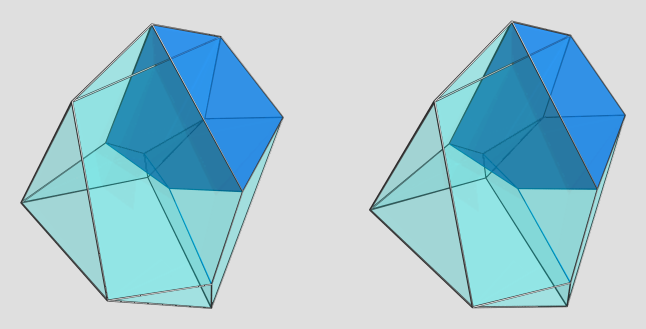
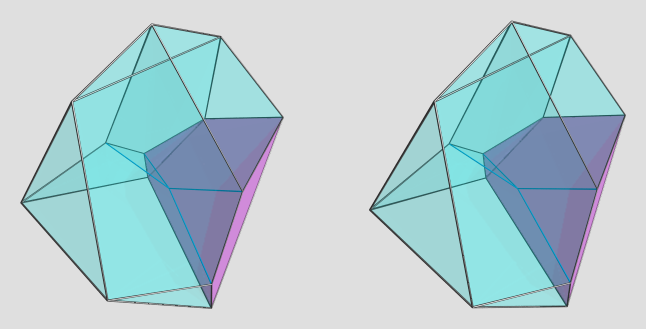
AFAICT, these cells are all congruent, so this sorta gives you a good view of the cell shape from different angles (albeit under various 4D projection foreshortenings as well ).
).
 It's still not so easy to get a good view of it, but I managed to find a serviceable viewpoint:
It's still not so easy to get a good view of it, but I managed to find a serviceable viewpoint:
This is a cell-centered projection, with the yellow cell being the one directly facing the 4D viewpoint (i.e., 90° to the 4D viewpoint). It appears to have 2 triangular faces, 2 tetragons, and 2 pentagons, all irregular. There are two other cells that lie on the near side from this viewpoint, each touching the yellow cell on a pentagonal face, and sharing a triangle with each other (seen at the top of the image).
As usual, the blue edges lie on the far side. As far as I can tell, there are only 4 of these, meeting at the antipodal vertex. This particular viewpoint is rather nice in that you can trace the shapes of the remaining cells with not too much difficulty by tracing the edge outlines.
Here's one of the other cells on the near side:

Here's the other one:

Here are the 4 cells on the far side of the polytope:




AFAICT, these cells are all congruent, so this sorta gives you a good view of the cell shape from different angles (albeit under various 4D projection foreshortenings as well
 ).
).- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:Hmm. This is a tough one. It looks like it has 14 (irregular) tetrahedral cells, all joining at rather sharp angles, which makes it really hard to find a good 4D viewpoint. I spent about 20 mins trying to find a good viewpoint, but couldn't.
This is the best image I could get after ~20 min's of trying. The yellow cell is the one facing the 4D viewpoint. The faint blue edges lie on the far side of the polytope. There are 4 other cells that lie on this side of the polytope, the rest lie on the far side.
According to the edge length classifier, there are 3 kinds of edges, with lengths approx 2.06, 2.46, and 2.88, respectively. As far as I can tell, all cells are congruent, with all 3 kinds of edges (1 edge of length 2.88, 2 edges of length 2.06, 3 edges of length 2.46). For every cell, there are 2 others that do not share any edges with it (i.e., they only touch at the vertices). Every cell shares at least 1 vertex with every other cell.
If you're interested in step prisms, probably the best bet would be to start with a larger duoprism, so the the result would have blunter angles, as that tends to be easier to visualize via projections.
P.S. It occurred to me that it might be useful to do a vertex-centered projection, so here's one:
Again, the faint blue edges are on the far side of the polytope. This viewpoint isn't that clear either, but at least if you focus on the edges emanating from the central vertex (the vertex the projection is centered on), you can sort of see the tetrahedral cells folded around it. It's not very clear, though. As I said, it has very sharp angles and so it's hard to get a good viewpoint on it.
As for the dual, let me get to that.
Good, but one thing I noticed is that there are actually two types of tetrahedra here. This can be illustrated by coloring each edge according to the length (red = short, blue = medium, and green = long for example). The tetrahedra are divided into two classes: those with one green edge and those with three green edges. BTW, it is not identical to the 6-simplex even though they share the same vertex/edge arrangement in 2D, but it appears as a 4D projection of a 6-simplex.
Anyways, I mentioned a class of swirl polychora, also derived from the n-n duoprisms. They are compounds of n-n duoprisms rotated like how three equilateral triangles can be placed in a regular nonagon, so the simplest non-trivial one is the so-called triangular duoprismatic triswirlchoron with 18 triangular antiprism cells (in two perpendicular sets of 9 cells each) and 54 tetrahedra. More about here: viewtopic.php?f=25&t=2231
P.S. the coordinates of the triangular duoprismatic triswirlchoron is the Cartesian product (P1) x (P1) where P1 is a unit equilateral triangle (resulting in a unit 3-3 duoprism), (P2) x (P2) where P2 is a unit equilateral triangle rotated 40 degrees with respect to P1, and (P3) x (P3) where P3 is a unit equilateral triangle rotated 80 degrees with respect to P1.
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Isogonal swirl polychora
What would be the result of doing that but with 2 different trigonal duoprisms instead of 3? (normal and rotated 60 degrees)
EDIT: Apparently that would be the triangular duoantiprism. Sorry, missed it.
EDIT: Apparently that would be the triangular duoantiprism. Sorry, missed it.
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
Mercurial, the Spectre wrote:[...]
Good, but one thing I noticed is that there are actually two types of tetrahedra here. This can be illustrated by coloring each edge according to the length (red = short, blue = medium, and green = long for example). The tetrahedra are divided into two classes: those with one green edge and those with three green edges.
Argh, I should've checked more carefully before making statements like that.

 I should have colored the edges differently, since the latest version of polyview allows doing that relatively easily (it used to be that you have to manually select those edges, the latest version now allows selecting them by length).
I should have colored the edges differently, since the latest version of polyview allows doing that relatively easily (it used to be that you have to manually select those edges, the latest version now allows selecting them by length).BTW, it is not identical to the 6-simplex even though they share the same vertex/edge arrangement in 2D, but it appears as a 4D projection of a 6-simplex.
A sufficiently high-dimensional simplex can project into any polytope with simplicial facets.
 So that's not saying very much.
So that's not saying very much.  (In fact, if you're willing to delete some edges, a sufficiently high-dimensioned simplex can project into any polytope, regardless of facet type. But that's kinda a useless statement because it doesn't really tell you anything useful.)
(In fact, if you're willing to delete some edges, a sufficiently high-dimensioned simplex can project into any polytope, regardless of facet type. But that's kinda a useless statement because it doesn't really tell you anything useful.)Anyways, I mentioned a class of swirl polychora, also derived from the n-n duoprisms. They are compounds of n-n duoprisms rotated like how three equilateral triangles can be placed in a regular nonagon, so the simplest non-trivial one is the so-called triangular duoprismatic triswirlchoron with 18 triangular antiprism cells (in two perpendicular sets of 9 cells each) and 54 tetrahedra. More about here: viewtopic.php?f=25&t=2231
P.S. the coordinates of the triangular duoprismatic triswirlchoron is the Cartesian product (P1) x (P1) where P1 is a unit equilateral triangle (resulting in a unit 3-3 duoprism), (P2) x (P2) where P2 is a unit equilateral triangle rotated 40 degrees with respect to P1, and (P3) x (P3) where P3 is a unit equilateral triangle rotated 80 degrees with respect to P1.
This sounds very interesting! I'm going to try to play with this a bit to see if I can construct these things.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
One of these days I might try to come up with a list of types of isogonal polychora. Bowers already has a list of 4D dice (which will be the duals of the isogonals) so I'll start from there.
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
username5243 wrote:One of these days I might try to come up with a list of types of isogonal polychora. Bowers already has a list of 4D dice (which will be the duals of the isogonals) so I'll start from there.
I've always been interested in cell-transitive polychora.
The regular polychora are of course the first of these. Then obviously the 4D Catalans. Then two of my favorites are also uniform: the bitruncated 24-cell and bitruncated 5-cell.
Another favorite is bidex, with 48 transitive tridiminished icosahedra. Its dual is also cell-transitive (albeit non-CRF), which is especially interesting.
Then there's the duoprisms, obviously, and their duals (what Wendy calls the tegums). The limiting shape of the duoprisms as the polygon degree grows is the duocylinder; the limiting shape of the tegums is the bicircular tegum (tegum product of two orthogonal circles).
Then the duoantiprisms, of which the grand antiprism is uniform, but the rest are not (AFAIK, none of them are CRF either besides gap).
Then there's the swirlprisms, the step-prisms, which are probably related to the discretizations of Bower's regular polytwisters.
Another related category that I'm not sure has been explored is the discrete Hopf fibration mapping of face-transitive 3D polyhedra, like e.g. the discrete Hopf mapping of the n-gonal bipyramids (i.e. duals of the 3D uniform prisms) or the duals of the uniform antiprisms. These may or may not be related to the swirlprisms / polytwisters, but it's along the same idea of using the Hopf fibration mapping to create transitive structures.
There's also the pyramid antiprisms (i.e., n-pyramid || dual n-pyramid), which if I didn't make a mistake ought to be vertex-transitive, so their duals also ought to be 4D dice.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:[...]
There's also the pyramid antiprisms (i.e., n-pyramid || dual n-pyramid), which if I didn't make a mistake ought to be vertex-transitive, so their duals also ought to be 4D dice.
Argh, nevermind, I wasn't thinking clearly. There are clearly two distinct classes of vertices in these.


- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
the gap (grand antiprism) isn't really a duoantiprism. THe bi-pentagonal duoantiprism (formed by alternating a decagonal doprism) has 20 pentagon antiprisms and 50 tetrahedra only. I do think other polygonal versions of gap are vertex transitive.
The pyramid antiprisms aren't vertex transitive - they're the same thing as antiprism bipyramids, which obviously won't be vertex transitive.
I'll make the list later, I think I may have discovered some new ones - turns out certain tesseractic uniform polychora (tat, sidpith, and rit) are vertex transitive under square duoprismatic symmetry - so they should have analogous constructions for other polygonal symmetries too that are vertex transitive.
Bowers actually has a page on his website where he lists all the dice up to 20 sides, found here:
http://www.polytope.net/hedrondude/dice4.htm
The pyramid antiprisms aren't vertex transitive - they're the same thing as antiprism bipyramids, which obviously won't be vertex transitive.
I'll make the list later, I think I may have discovered some new ones - turns out certain tesseractic uniform polychora (tat, sidpith, and rit) are vertex transitive under square duoprismatic symmetry - so they should have analogous constructions for other polygonal symmetries too that are vertex transitive.
Bowers actually has a page on his website where he lists all the dice up to 20 sides, found here:
http://www.polytope.net/hedrondude/dice4.htm
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
Another idea that just occurred to me: take an n,n-duoprism, Stott-expand its cells outward radially and take the convex hull. Basically, the result looks like the convex hull of the compound of a 2n,n-duoprism with an n,2n-duoprism, which should be vertex-transitive. So the dual should be cell-transitive.
The duoprism is just a special case, of course. Take any cell-transitive, vertex-transitive swirlprism, and Stott-expand the cells. If my guess is correct it should also result in a vertex-transitive polytope, so the dual should again be cell-transitive.
The duoprism is just a special case, of course. Take any cell-transitive, vertex-transitive swirlprism, and Stott-expand the cells. If my guess is correct it should also result in a vertex-transitive polytope, so the dual should again be cell-transitive.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
Yeah that should work.
Wait, I just thought: would a Stott-expansion of deca or cont be vertex transitive? It might be if the expanded duoprisms rae...
Wait, I just thought: would a Stott-expansion of deca or cont be vertex transitive? It might be if the expanded duoprisms rae...
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
Here's an example made by taking the dual of the convex hull of the union of a 5,10-duoprism with a 10,5-duoprism:
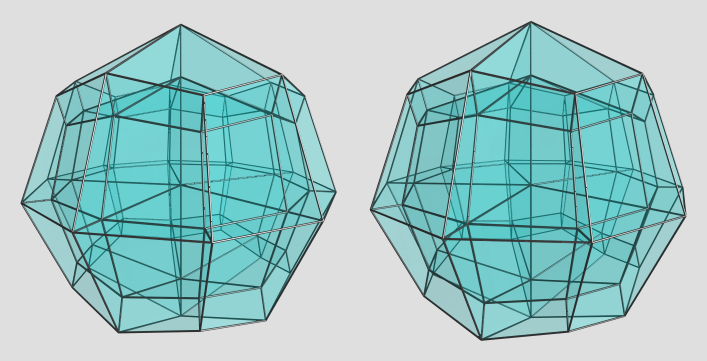
(Due to the large number of edges, I turned on clipping, so what you see here is only the cells on the near side.)
AFAICT, it should be cell-transitive, and the cell shape is some kind of hexahedron with tetragonal faces (distorted cubes). There are 100 cells and 120 vertices.
For the case n=4, the Stott expansion coincides with the runcinated tesseract, so the dual would be a 4D Catalan. For the other cases, the result would not be a Catalan, but would nevertheless be cell-transitive, and so would serve as 4D dice. In general, the number of cells would be 4*n2, so you would get dice of these sizes:
n=2: 16 (coinciding with the 16-cell[*])
n=3: 36
n=4: 64 (dual of runcinated tesseract)
n=5: 100
n=6: 144
... etc.

(Due to the large number of edges, I turned on clipping, so what you see here is only the cells on the near side.)
AFAICT, it should be cell-transitive, and the cell shape is some kind of hexahedron with tetragonal faces (distorted cubes). There are 100 cells and 120 vertices.
For the case n=4, the Stott expansion coincides with the runcinated tesseract, so the dual would be a 4D Catalan. For the other cases, the result would not be a Catalan, but would nevertheless be cell-transitive, and so would serve as 4D dice. In general, the number of cells would be 4*n2, so you would get dice of these sizes:
n=2: 16 (coinciding with the 16-cell[*])
n=3: 36
n=4: 64 (dual of runcinated tesseract)
n=5: 100
n=6: 144
... etc.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
And here's a render of the n=3 case:
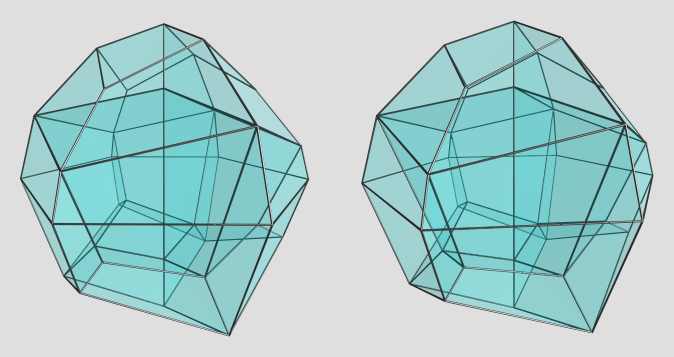
I'm really liking this construction, it yields nice hexahedral cells for the dice's facets.

I'm really liking this construction, it yields nice hexahedral cells for the dice's facets.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
I agree, these things are neat.
Speaking of interesting 4D dice, one of the more interesting ones should be the dual of spic (x3o4o3x) which as 144 sides shaped like the dual of a square antiprism. Probalby the most interesting one imo outside of the duals of the snub 24 and grand antiprism.
Speaking of interesting 4D dice, one of the more interesting ones should be the dual of spic (x3o4o3x) which as 144 sides shaped like the dual of a square antiprism. Probalby the most interesting one imo outside of the duals of the snub 24 and grand antiprism.
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
The inevitable next question is, what if we take this to the extreme? I.e., take the limit as n approaches infinity. The result should be the dual of the "runcinated duocylinder" (the result of Stott-contracting the two toroidal surfaces of a duocylinder and taking the convex hull), which is a kind of ridged tegum; its two bounding 3-manifolds would look sorta like raising a circular ridge around the duocylinder's surfaces. If I'm not mistaken, it should be the equivalent of taking the convex hull of a duocylinder with two circles raised above its two toroidal surfaces.
Probably an analogous operation applies to all the regular polytwisters: raise a circular ridge above each twistor, and the result should be chorix-transitive, I think? Well, if you regard the ridge as part of the twistor, then it's definitely still regular, except I'm not sure if you can call it a twistor anymore. Or it may be uniform if the twistor splits into multiple strips around the ridge? No matter what, this is really cool stuff.
Or it may be uniform if the twistor splits into multiple strips around the ridge? No matter what, this is really cool stuff. 
Probably an analogous operation applies to all the regular polytwisters: raise a circular ridge above each twistor, and the result should be chorix-transitive, I think? Well, if you regard the ridge as part of the twistor, then it's definitely still regular, except I'm not sure if you can call it a twistor anymore.
 Or it may be uniform if the twistor splits into multiple strips around the ridge? No matter what, this is really cool stuff.
Or it may be uniform if the twistor splits into multiple strips around the ridge? No matter what, this is really cool stuff. 
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:If you can compute coordinates for 4D objects you're interested in (convex only, unfortunately), I can make polyview models for them and render them.
How about the disphenoidal diacosioctacontaoctachoron (288-cell)? Its coordinates are all permutations of sign and location of:
{1, 0, 0, 0}
{√2/2, √2/2, 0, 0}
{1/2, 1/2, 1/2, 1/2}
- Mecejide
- Trionian
- Posts: 86
- Joined: Sun Mar 10, 2019 1:58 am
- Location: Nethlekempt Farrows
Re: Isogonal swirl polychora
Mecejide wrote:quickfur wrote:If you can compute coordinates for 4D objects you're interested in (convex only, unfortunately), I can make polyview models for them and render them.
How about the disphenoidal diacosioctacontaoctachoron (288-cell)? Its coordinates are all permutations of sign and location of:
{1, 0, 0, 0}
{√2/2, √2/2, 0, 0}
{1/2, 1/2, 1/2, 1/2}
That's the dual of the bitruncated 24-cell, isn't it? This one is a toughie, because it's all tetrahedral cells. Simplicial polytopes are generally the hardest to work with in projections because it's hard to discern where the cells are. Nevertheless, here's an attempt:
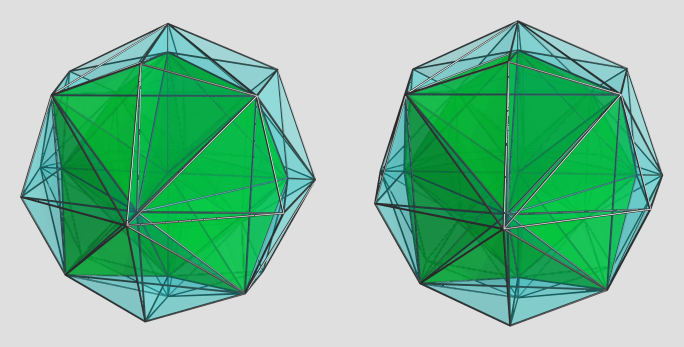
Because of the large number of edges and cells, which make it hard to discern individual cells, I decided to highlight the cluster of cells surrounding the central vertex (which is the nearest vertex to the 4D viewpoint). The contrast with the outer cells make the latter more easily discernible IMO. The green blob is actually a cluster of 24 (non-regular) tetrahedra, 3 around every diagonal edge emanating from the central vertex. As can be easily seen in the front of the projection volume, the axial edges have 8 cells surrounding them. There are many other cells here that are hard to pick out individually because of their sheer number.
Note that to declutter the image I turned on visibility clipping, so only the near side cells are shown here. The far side cells are clipped to keep some semblance of sanity in the resulting image.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
Yeah that's the dual of the bitruncated 24; a simpler one of the same sort is the disphenoidal triacontachoron, the dual of the decachoron (bitruncated 5).
One interesting group of vertex-transitive polytopes is this sort of thing - take a polytope with single (not duble) pennic/icoic symmetry, with a second copy from the opposite orientation, take the convex hull, and the result is a vertex-transitive polychoron - so the duals are fair dice. The ones with the regular 5-cell and 24-cell are Catalans; the others are new. I don't have coordinates for these on hand for the 24-cell based ones, but the ones derived from 5-cell truncates should be easy - I believe it works if you take the coordinates of a 5-cell truncate (that are on your website, quickfur) for one copy, and the second copy by just flipping all the signs.
One interesting group of vertex-transitive polytopes is this sort of thing - take a polytope with single (not duble) pennic/icoic symmetry, with a second copy from the opposite orientation, take the convex hull, and the result is a vertex-transitive polychoron - so the duals are fair dice. The ones with the regular 5-cell and 24-cell are Catalans; the others are new. I don't have coordinates for these on hand for the 24-cell based ones, but the ones derived from 5-cell truncates should be easy - I believe it works if you take the coordinates of a 5-cell truncate (that are on your website, quickfur) for one copy, and the second copy by just flipping all the signs.
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
How about the convex hull of 2 rectified 24-cells?
{0, 1, 1, 1}
{0, √2/2, √2/2, √2}
{1/2, 1/2, 1/2, 3/2}
{0, 1, 1, 1}
{0, √2/2, √2/2, √2}
{1/2, 1/2, 1/2, 3/2}
- Mecejide
- Trionian
- Posts: 86
- Joined: Sun Mar 10, 2019 1:58 am
- Location: Nethlekempt Farrows
Re: Isogonal swirl polychora
Mecejide wrote:How about the convex hull of 2 rectified 24-cells?
{0, 1, 1, 1}
{0, √2/2, √2/2, √2}
{1/2, 1/2, 1/2, 3/2}
Whoa, this one turned out far more interesting than I expected! It's a pretty little polychoron with 48 cubes and 192 (irregular) square antiprisms:
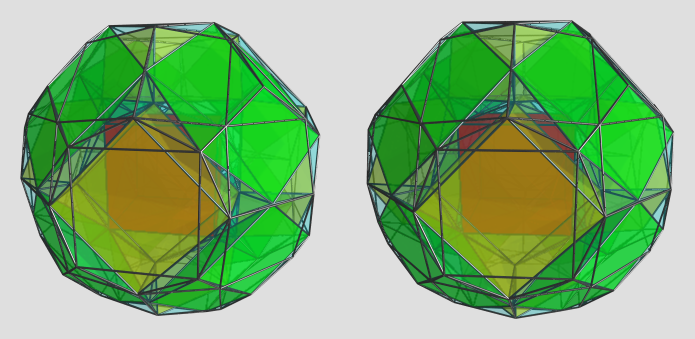
Surprisingly, there are no "filler" cells like tetrahedra or triangular prisms; it's just regular cubes and squished square antiprisms. Especially interesting is how at every vertex 2 cubes and 6 square antiprisms meet. A totally unexpected structure (for me!).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:Mecejide wrote:How about the convex hull of 2 rectified 24-cells?
{0, 1, 1, 1}
{0, √2/2, √2/2, √2}
{1/2, 1/2, 1/2, 3/2}
Whoa, this one turned out far more interesting than I expected! It's a pretty little polychoron with 48 cubes and 192 (irregular) square antiprisms:
<rest of post snipped>
Shouldn't it have 144 square antiprisms, not 192?
- username5243
- Trionian
- Posts: 128
- Joined: Sat Mar 18, 2017 1:42 pm
Re: Isogonal swirl polychora
Ah you're right, mea culpa. 

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Isogonal swirl polychora
quickfur wrote:Mecejide wrote:How about the convex hull of 2 rectified 24-cells?
{0, 1, 1, 1}
{0, √2/2, √2/2, √2}
{1/2, 1/2, 1/2, 3/2}
Whoa, this one turned out far more interesting than I expected! It's a pretty little polychoron with 48 cubes and 192 (irregular) square antiprisms:
Surprisingly, there are no "filler" cells like tetrahedra or triangular prisms; it's just regular cubes and squished square antiprisms. Especially interesting is how at every vertex 2 cubes and 6 square antiprisms meet. A totally unexpected structure (for me!).
I call it the biambotetracontaoctachoron. There's a wikipedia entry on it (see https://en.wikipedia.org/wiki/Rectified ... _polytopes)
How about the alternated truncated octahedral prism (aka the pyritohedral icosahedral antiprism)? It's not uniform. Coordinates are:
(0, ±1/2, ±0.80901699437494742410, 0.35355339059327376220) (all even permutations for the first three coordinates, for a total of 12 vertices)
(±1/2, 0, ±0.80901699437494742410, -0.35355339059327376220) (same as above for the first three coordinates)
And also its dual.
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Isogonal swirl polychora
Mercurial, the Spectre wrote:[...]
How about the alternated truncated octahedral prism (aka the pyritohedral icosahedral antiprism)? It's not uniform. Coordinates are:
(0, ±1/2, ±0.80901699437494742410, 0.35355339059327376220) (all even permutations for the first three coordinates, for a total of 12 vertices)
(±1/2, 0, ±0.80901699437494742410, -0.35355339059327376220) (same as above for the first three coordinates)
And also its dual.
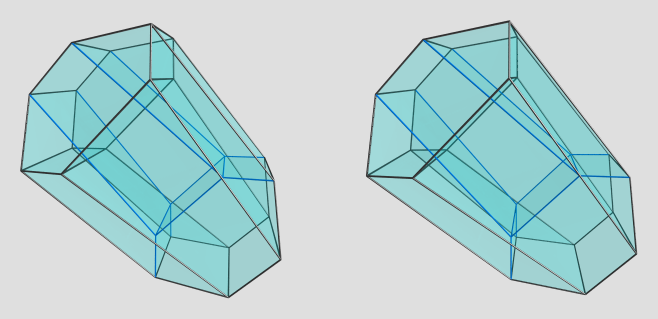
Here's the same projection in a different orientation:
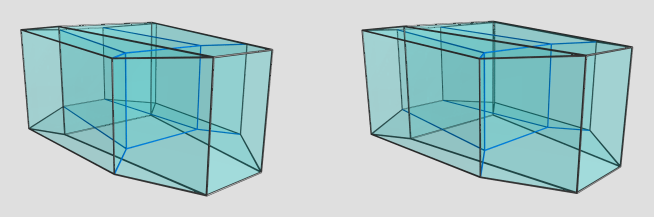
I'm not sure what to make of this; it looks like the prism of an irregular hexagonal prism. Is there a specific 4D viewpoint you have in mind?
Anyway, here's the dual:
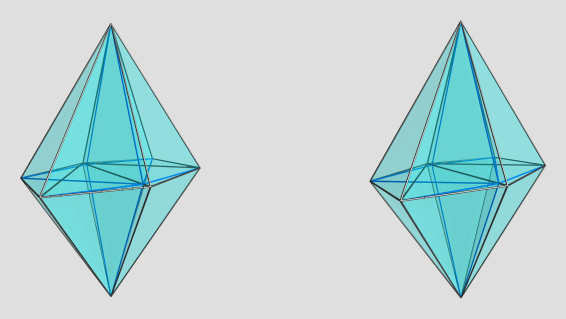
Not sure what to make of this either. It does look like a pretty little diamond shape, though.
Again, if you have a specific 4D viewpoint in mind, do let me know.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
47 posts
• Page 1 of 2 • 1, 2
Who is online
Users browsing this forum: No registered users and 50 guests
