Can Chamfer generalized to higher-dimensions?
For example, in case of truncation, higher-order truncation can be defined, like cantellation, runcination, sterication, etc.
According to Wikipedia, Chamfering (edge-truncation) is an operation for polyhedra, similar to expansion, but differ to that because of maintaining original vertices.
In here what I wanna ask is whether higher-order Chamfering can be defined.
For example, in that similar to expansion, can we generalize it to ridge-truncation (that cuts ridges of polytope, similar to expansion, but remaining vertex, edge, …, peak)?
Can Chamfer generalized to higher-dimensions?
8 posts
• Page 1 of 1
Re: Can Chamfer generalized to higher-dimensions?
Chamfering exists in all dimensions, and is perfectly generalised to all levels of surtope. I use the word 'bevel' for it.
Vertex-champhering is simply truncation.
In essence, for a figure constructed by Wythoff's construction, champering consists of an intersection of a regular polytope and the dual of some rectate. The edge-champer is the regular polytope xooo... intersecting with the dual of the polytope at the edges, ie omoooo.. A hedro-champer would intersect xoooo with oomooo..., where these are the individual marks on the nodes.
Since the Conway-Hart constructions treat any figure as a regular, and derive the new figure in the same way that the regular gives a new figure, then you can chamfer any polytope.
The normal n-chamfer would be a margin-chamfer, which seeks to round the boundaries between the faces. In essence, imagine a tesseract of wood. The margin-chamfer would be as if you were to plane the sharp corners at 45 degrees to the cube-cube interface. This does not chamfer the edge, but the boundry between the faces (margins).
Vertex-champhering is simply truncation.
In essence, for a figure constructed by Wythoff's construction, champering consists of an intersection of a regular polytope and the dual of some rectate. The edge-champer is the regular polytope xooo... intersecting with the dual of the polytope at the edges, ie omoooo.. A hedro-champer would intersect xoooo with oomooo..., where these are the individual marks on the nodes.
Since the Conway-Hart constructions treat any figure as a regular, and derive the new figure in the same way that the regular gives a new figure, then you can chamfer any polytope.
The normal n-chamfer would be a margin-chamfer, which seeks to round the boundaries between the faces. In essence, imagine a tesseract of wood. The margin-chamfer would be as if you were to plane the sharp corners at 45 degrees to the cube-cube interface. This does not chamfer the edge, but the boundry between the faces (margins).
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Can Chamfer generalized to higher-dimensions?
Thanks for your reply.
Then... what's shape of cells of ridge-truncated tesseract and ridge-truncated 120-cell?
Are some of them non-uniform like hexagons of chamfered dodecahedron?
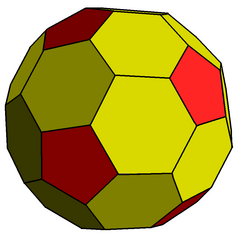
https://en.wikipedia.org/wiki/Chamfer_(geometry)
https://en.wikipedia.org/wiki/Chamfered_dodecahedron
Then... what's shape of cells of ridge-truncated tesseract and ridge-truncated 120-cell?
Are some of them non-uniform like hexagons of chamfered dodecahedron?

https://en.wikipedia.org/wiki/Chamfer_(geometry)
https://en.wikipedia.org/wiki/Chamfered_dodecahedron
- hy.dodec
- Dionian
- Posts: 19
- Joined: Sun Aug 13, 2017 11:12 am
Re: Can Chamfer generalized to higher-dimensions?
Chamfering is quite an interesting operation, when being transfered onto higher spaces too.
In contrast to Wendy's beveling operation chamfering is being applied only to the edges of some regular polytope.
In fact within 4D it flatens the former edges into new elongated rhombohedral cells (just as in 3D there occured elongated rhombs aka axially symmetric hexagons as new faces). Additionally the former regular polyhedral cells get rasped down into chamfered versions thereof.
But it should be noted also that those new cells underneath the former chamfered off edges - yes, indeed, the former vertices are NOT maintained thereby, within 4D alike as in 3D, rather it is only their radial direction which is being kept, not the actual distance! - will have elongated hexagonal faces in parallel to the replaced edge, which then attach to the thereby chamfered cells, and further tetragonal ones, which connect inbetween the hexagons and connect to the tips. These tetragons generally will be kites only. Just within the case of a fourfold symmetry around the edges of the former regular polychoron, these kites become true rhombs.
This above observation then is why that only the chamfered 16-cell can be made with all edges being equal sized. - More details to that figure can be found here: https://bendwavy.org/klitzing/incmats/abx3ooo3ooc4odo_zx.htm.
In that very case the new axial cells underneath the former edges happen to be bi-augmented axially elongated cuboctahedra.
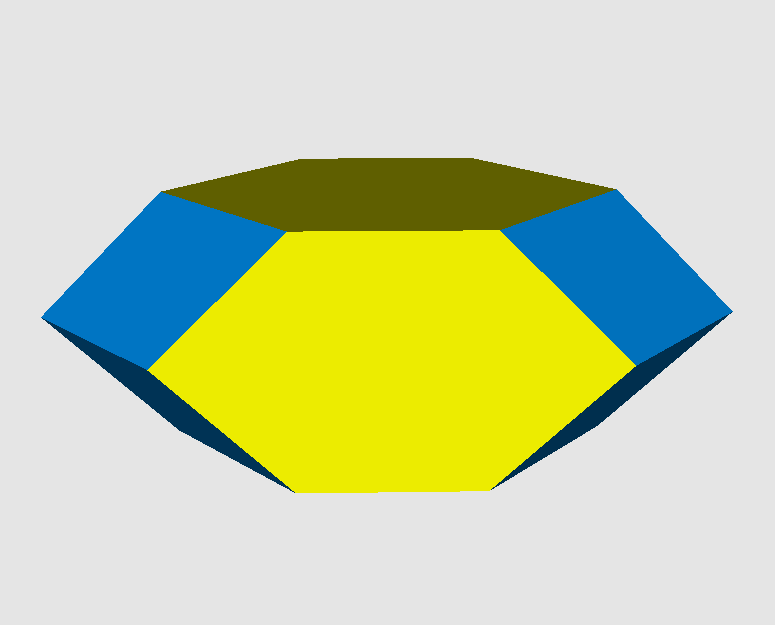
And the former tetrahedral cells get reduced into chamfered tetrahedra which happen to look like tetrahedrally only being truncated cubes:
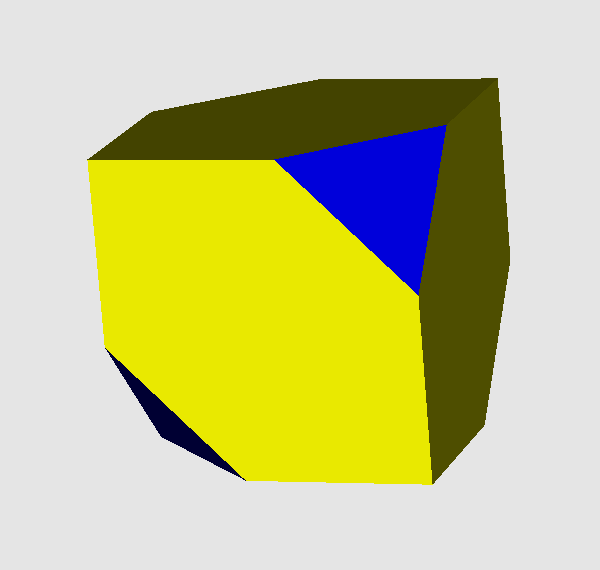
Thus the yellow axial hexahedra will connect both types of cells, whereas the dark blue triangles will connect to those again, and the lighter blue rhombs will connect to those in turn. The tips of those axial cells then will be situated slightly underneath the 8 vertices of the original encasing 16-cell.
--- rk
In contrast to Wendy's beveling operation chamfering is being applied only to the edges of some regular polytope.
In fact within 4D it flatens the former edges into new elongated rhombohedral cells (just as in 3D there occured elongated rhombs aka axially symmetric hexagons as new faces). Additionally the former regular polyhedral cells get rasped down into chamfered versions thereof.
But it should be noted also that those new cells underneath the former chamfered off edges - yes, indeed, the former vertices are NOT maintained thereby, within 4D alike as in 3D, rather it is only their radial direction which is being kept, not the actual distance! - will have elongated hexagonal faces in parallel to the replaced edge, which then attach to the thereby chamfered cells, and further tetragonal ones, which connect inbetween the hexagons and connect to the tips. These tetragons generally will be kites only. Just within the case of a fourfold symmetry around the edges of the former regular polychoron, these kites become true rhombs.
This above observation then is why that only the chamfered 16-cell can be made with all edges being equal sized. - More details to that figure can be found here: https://bendwavy.org/klitzing/incmats/abx3ooo3ooc4odo_zx.htm.
In that very case the new axial cells underneath the former edges happen to be bi-augmented axially elongated cuboctahedra.

And the former tetrahedral cells get reduced into chamfered tetrahedra which happen to look like tetrahedrally only being truncated cubes:

Thus the yellow axial hexahedra will connect both types of cells, whereas the dark blue triangles will connect to those again, and the lighter blue rhombs will connect to those in turn. The tips of those axial cells then will be situated slightly underneath the 8 vertices of the original encasing 16-cell.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Can Chamfer generalized to higher-dimensions?
Klitzing described the chamfered 16-cell. Every regular polychoron has a chamfered version, in which the edge, instead of the vertex, is truncated in a manner that resembles a process towards rectification.
The chamfered 5-cell has 5 chamfered tetrahedra and 10 D3h-symmetric polyhedra that basically is composed of 6 kites (3 at the top and 3 at the bottom arranged like a triangle subdivided into 3 identical kites, and 3 rectangular-symmetric hexagons connecting them with their centers lying on the xy-plane). Topologically, the 10 D3h-symmetric cells are not zonohedra because the kites are not centrally symmetric.
The chamfered tesseract has 8 chamfered cubes and 32 of the same D3h-symmetric polyhedra described before.
The chamfered 16-cell is described by Klitzing.
The chamfered 24-cell has 24 chamfered octahedra and 96 of the same D3h-symmetric polyhedra.
The chamfered 120-cell has 120 chamfered dodecahedra and 1200 of the same D3h-symmetric polyhedra.
The chamfered 600-cell has 600 chamfered tetrahedra and 720 D5h-symmetric polyhedra that are analogues of the ones found from the chamfered 5-cell and the chamfered 16-cell. There are 10 kites (5 top, 5 bottom) with 5 rectangular-symmetric hexagons connecting them in much the same way as the previous ones.
Except for the chamfered 16-cell, they cannot be made into zonochora due to restrictions in topological variations if a rhomb is to be used in place of a kite.
Honestly, there are no easy names for these possibly-zonohedral kite-hexagon polyhedra, but I would call them n-deltoidal hexagoprismohedra, in reference of containing only kites and hexagons with prismatic symmetry. The bi-augmented axially elongated cuboctahedra can also be called the tetradeltoidal hexagoprismohedron.
The chamfered 5-cell has 5 chamfered tetrahedra and 10 D3h-symmetric polyhedra that basically is composed of 6 kites (3 at the top and 3 at the bottom arranged like a triangle subdivided into 3 identical kites, and 3 rectangular-symmetric hexagons connecting them with their centers lying on the xy-plane). Topologically, the 10 D3h-symmetric cells are not zonohedra because the kites are not centrally symmetric.
The chamfered tesseract has 8 chamfered cubes and 32 of the same D3h-symmetric polyhedra described before.
The chamfered 16-cell is described by Klitzing.
The chamfered 24-cell has 24 chamfered octahedra and 96 of the same D3h-symmetric polyhedra.
The chamfered 120-cell has 120 chamfered dodecahedra and 1200 of the same D3h-symmetric polyhedra.
The chamfered 600-cell has 600 chamfered tetrahedra and 720 D5h-symmetric polyhedra that are analogues of the ones found from the chamfered 5-cell and the chamfered 16-cell. There are 10 kites (5 top, 5 bottom) with 5 rectangular-symmetric hexagons connecting them in much the same way as the previous ones.
Except for the chamfered 16-cell, they cannot be made into zonochora due to restrictions in topological variations if a rhomb is to be used in place of a kite.
Honestly, there are no easy names for these possibly-zonohedral kite-hexagon polyhedra, but I would call them n-deltoidal hexagoprismohedra, in reference of containing only kites and hexagons with prismatic symmetry. The bi-augmented axially elongated cuboctahedra can also be called the tetradeltoidal hexagoprismohedron.
- Mercurial, the Spectre
- Trionian
- Posts: 106
- Joined: Mon Jun 19, 2017 9:50 am
Re: Can Chamfer generalized to higher-dimensions?
Umm... How about ridge-truncation?
Moving facet apart and outward, but also maintain the original vertices...
Can this operation possible in all higher-dimensions?
If possible, Could you give an example in 4D?
Moving facet apart and outward, but also maintain the original vertices...
Can this operation possible in all higher-dimensions?
If possible, Could you give an example in 4D?
- hy.dodec
- Dionian
- Posts: 19
- Joined: Sun Aug 13, 2017 11:12 am
Re: Can Chamfer generalized to higher-dimensions?
hy.dodec wrote:Moving facet apart and outward, but also maintain the original vertices...
Can this operation possible in all higher-dimensions?
If possible, Could you give an example in 4D?
Here comes a detailed description of one of the 4D examples:
your quest quite generally comes down to this:
first bit = conway expansion, e.g. from xPoQoRo to xPoQoRx
second bit = but apiculating the new vertex figure facets
in such a way that the laterals of those apiculations become corealmic with those other cells
Just consider this one for example:
first bit: x3o3o3o = pen -> x3o3o3x = spid
second bit: plus apiculating one subset of the tets in such a pyramidal height, that the trips get symmetrical elongated triangular dipyramids here the height and thus the lacing edge size of those triangular pyramids has to be derived from the environment.
Here we consider the unit-edged spid first. Its 4D circumradius R then is 1 too. The 3D circumradius r of the trip cells is sqrt(7/12), accordingly the trip-center-radius of spid is sqrt(R^2-r^2)=sqrt(1-7/12)=sqrt(5/12)
Now consider some y-scaled pen y3o3o3o.
That one has a circumradius R of y*sqrt(2/5). Here the edges of those are the elements, which become the trips while expansion. Thus we have to consider the circumradius r of the edge, which is simply y/2. Accordingly the edge-center-radius of the y-pen is sqrt(R^2-r^2)=y*sqrt(2/5-1/4)=y*sqrt(3/20)
Now these 2 elements have to be corealmic, that is, we have to equate these radii, sqrt(5/12)=y*sqrt(3/20), therefrom deriving y=sqrt(100/36)=sqrt(25/9)=5/3
Therefore the searched for apiculated polychoron thus is the convex hull of the compound of x3o3o3x (x=unit edge) plus y3o3o3o (y=5/3 edge) or just xy3oo3oo3xo&#zc, where the y surely is a pseudo-edge only, and the lacing edge c, i.e. the lacing edge of those apiculating pyramids are still to be calculated. But y=5/3 and the height of the unit trip is 1. Thus the pyramid itself has height h=(5/3-1)/2=1/3. The circumradius of the regular unit triangle is r=1/sqrt(3), therefore c=sqrt(r^2+h^2)=sqrt(1/3+1/9)=sqrt(4/9)=2/3
Further it can be observed, that xy3oo3oo3xo&#zc surely allows for a Stott contraction wrt. the first node, then resulting in oa3oo3oo3xo&#zc, where a=y-x=5/3-1=2/3 as well. But still those a's are pseude edges! - It appears that this contracted figure is not new, rather it is nothing but o3m3o3o or tibbid, i.e. the dual of o3x3o3o or rap.
Thus the above derived polychoron is nothing but a Stott expansion of tibbid. Its cells would be 10 elongated versions of the cells of tibbid, i.e. elongated triangular dipyramids xy2xo3oo&#zc, plus 5 tetrahedra x3o3o.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Can Chamfer generalized to higher-dimensions?
Thanks for all replies!
Sorry, I missed out a condition...
What about just moving facet apart, but maintain original vertices, edges, faces, …, j-faces, …, peaks
Sorry for asking again

Sorry, I missed out a condition...
What about just moving facet apart, but maintain original vertices, edges, faces, …, j-faces, …, peaks
Sorry for asking again


- hy.dodec
- Dionian
- Posts: 19
- Joined: Sun Aug 13, 2017 11:12 am
8 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 26 guests
