Bialternatosnub is my own term for bilateral alternatosnub with the word alternatosnub meaning "alternate snubbing." i.e. the vertices are halved similar to a full snub but preserving bilateral symmetry instead of making it chiral. Note that this topic will focus on regular polytopal bases. I discovered the process myself while experimenting with orthogonal 3D projections of duoprisms in GeoGebra.
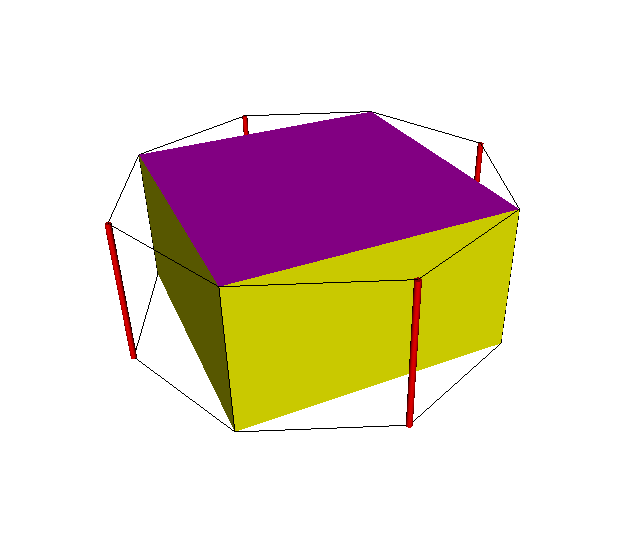
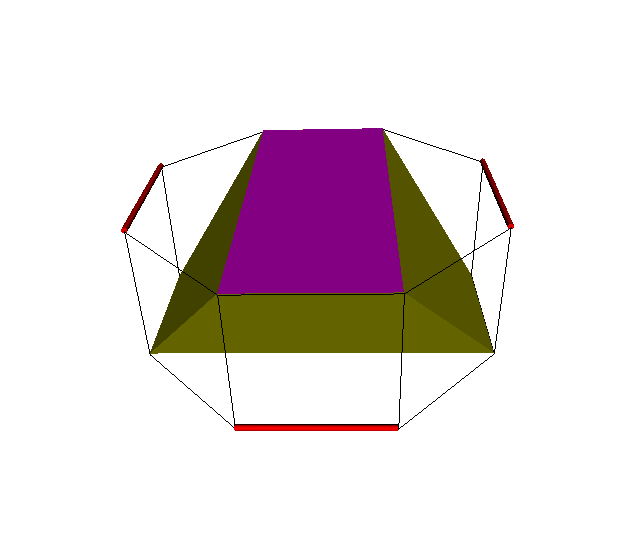
IMPORTANT NOTICE: Bialternatosnubbing is not a commutative operation, so s2s4x (a rectangular trapezoprism, basically a D2d-symmetric cube with 2 rectangles and 4 lateral trapezoidal faces) and s4s2x (a square prism) are not geometrically the same (although in some cases, such as these pairs, are topologically the same polyhedron). It can also be applied to tilings and honeycombs as well. They are isogonal, so their duals will have congruent facets.
Introduction
Bialternatosnub polytopes are derived from omnitruncated polytopes that have been alternated in a different way compared to full snubs preserving bilateral symmetry along the hyperplanes of the alternated facets. The base polytopes will be from regular polytopes, tilings, or honeycombs of Schläfli symbol {p,q,..,y,z} with shorthand notation s{p}s{q}...s{z}x with the last letter being an even number (z in this case). If the last letter represents an odd number, then the result is a holosnub instead of a full-fledged bialternatosnub. (example: s3s3s4x denoting a bialternatosnub 16-cell which contains 16 icosahedra, 32 triangular prisms (represented as s3s2x or bialternatosnub trigonal dihedron), 24 rectangular trapezoprisms (s2s4x or bialternatosnub square hosohedron), 8 pyritohedral rhombicuboctahedra, and 96 wedges as sectioning facets. It has no uniform realization. Fun fact: an x,u-variant of s3s3s4x occurs as a diminishing of prissi).
In 2D, the bialternatosnub of {2p} is the 2p-gon itself with p-gonal symmetry. Its uniform (and regular) realization is none other than the 2p-gon itself.
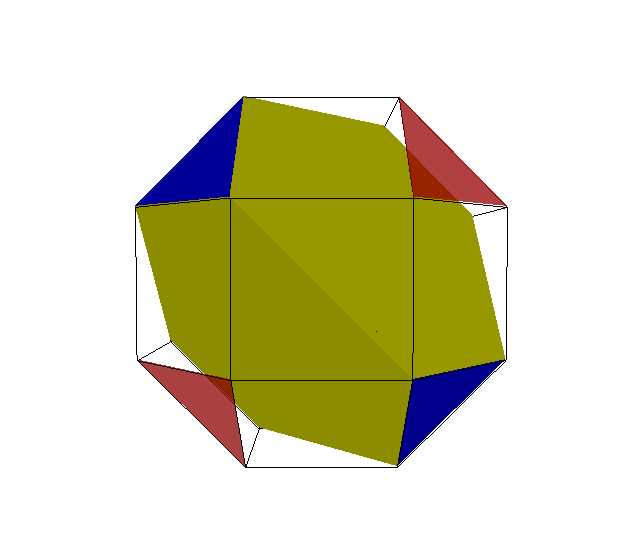
In 3D, the bialternatosnub of {p,2q} has faces of type sPs (same as the p-gon), s2Qx (mentioned before) with trapezoidal faces as sectioning facets. Its uniform realization is xPo2Qx (cantellated {p,2q}). Example is the bialternatosnub {3,4} which turns out to be a pyritohedral rhombicuboctahedron.
In 4D, the bialternatosnub of {p,q,2r} has cells of type sPsQs, sQs(2R)x, sPs2x, s2s(2R)x with wedges (triangular prisms) as sectioning facets. In general, like the 4D snubs, there is no uniform realization.
One of my favorites is the bialternatosnub 2-4 duoprism (s2s2s4x) which I discovered months ago. It is nonuniform and can be derived from the 4-8 duoprism. It has tetrahedra, rectangular trapezoprisms and wedges for cells (plus square faces that are actually derived from the cubes; these alternate with the tetrahedra). In fact the variant with squares and regular tetrahedra appears as a diminishing of rit (rectified tesseract).
I'd love to see its dual that has 16 identical bilaterally symmetric triangular prism cells (basically the dual of s2s2s4x's vertex figure, which is a bilaterally symmetric trigonal bipyramid) but I don't have Stella4D to check it out.
Best to you out there guys, as this is my first post