List of uniform honeycombs
99 posts
• Page 4 of 4 • 1, 2, 3, 4
Re: List of uniform honeycombs
My name is Eric#0289. I am also EricABQ on the Miraheze wiki.
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
It's been 6 years since I posted my first of uniform honeycombs. To celebrate, I've published a website about uniform honeycombs, in the style of Bowers' uniform polychora website: https://ericbinnendyk.github.io/website/honeycombs.html
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
Over the past few months, I've been sharing my new honeycomb discoveries with Username5243 over discord. I will be posting these discoveries here for reference.
I found several new members of the gyrate and elongate regiments, by viewing them as stacks of slab honeycombs and faceting the slabs.
I found several new members of the gyrate and elongate regiments, by viewing them as stacks of slab honeycombs and faceting the slabs.
- Octet is a stack of trataps (triangular tiling antiprisms). Tratap has two other regiment members (not counting subdivisions of trats into azaps): ditathahap and ditathatap (see the spreadsheet for details). A stack of ditathahaps is ohtrah (cho verf) and a stack of ditathataps is tehtrah (oho verf). But if you alternate between two of these three slabs on alternate layers, it gives three new uniform honeycombs: tratap + ditathahap, tratap + ditathatap, and ditathahap + ditathatap. (The last one actually comes in two forms, one with stacks of azaps and one with trats, but I'm excluding the former from the main list because it has coplanar faces in its verf.)
- Gytoh is also a stack of trataps, so it gives five new uniform honeycombs: ditathatap+ditathatap, ditathahap+ditathahap, tratap+ditathatap, tratap+ditathahap, and ditathatap+ditathahap.
- Gyetoh is a stack of alternating trataps and trattips (triangular tiling prisms). The trattips have o3o3o3*a prism symmetry so they act like they have three regiment members: trattip, ditathap1 (has trips touching octs), and ditathap2 (has trips touching tets). All the combinations of trattip members alternating with tratap members lead to eight new uniform honeycombs in addition to gyetoh.
- Etoh is also a stack of alternating trataps and trattips, but unlike gyetoh, etoh's symmetries allow us to map trips onto adjacent trips by turning the layer upside down. If we replace trattip by ditathap1 or ditathap2, the result is no longer uniform. Thus, the etoh regiment contains two new uniform honeycombs: ditathatap+trattip and ditathahap+trattip.
- Regyetoh (retroelongated gytoh) has eight other regiment members analogous to gyetoh.
- Retoh (retroelongated octet) has two other regiment members analogous to etoh.
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
On the Discord, _Geometer mentioned finding a uniform member of the squatap (square tiling antiprism) regiment. (Squatap itself is scaliform). It has tets and azaps. The verf is the blend of two wedges with square bases; a faceting of a square antipodium. It is also half of an oho. I propose the name "Spinosquare tiling hemiantiprism" for this, similar to the polyteron nophap (spinopentachoric hemiantiprism).
In fact, _Geometer described three members of the squatap regiment, whose verfs are half of co, cho, and oho. The other two are non-uniform scaliforms. I call them "Square tiling antiprism", "Square tiling hemiantiprism" (I used to give this name to o~x o~x || o~x x~o, but I now call that "apeirogonal antiprism pseudoprismatic honeycomb"), and "Spinosquare tiling hemiantiprism" respectively.
In fact, _Geometer described three members of the squatap regiment, whose verfs are half of co, cho, and oho. The other two are non-uniform scaliforms. I call them "Square tiling antiprism", "Square tiling hemiantiprism" (I used to give this name to o~x o~x || o~x x~o, but I now call that "apeirogonal antiprism pseudoprismatic honeycomb"), and "Spinosquare tiling hemiantiprism" respectively.
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
I also found some more members of the prismatic honeycombs' regiments. The ones I found involve blending the honeycombs with polygon-apeirogon duoprisms, but I suspect some prismatic honeycombs have many other regiment members yet to be discovered.
First, prismatic honeycombs made from tilings containing n-gons can be blended with n-gonal apeirogonal duoprisms. However, no more than one of them can blend around each lateral edge of a prism (corresponding to a vertex in the original tiling). To find blendings that are uniform honeycombs, we need to find ways to color one type of face of a uniform tiling so that exactly one face around each vertex is colored and the tiling is still vertex transitive under the coloring.
I know of several ways to do this:
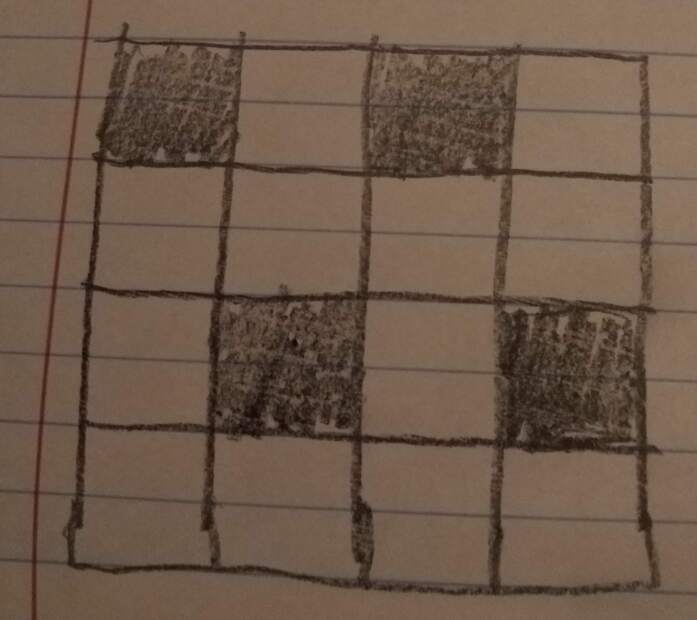
Blend 1/4 of the squares in squat (already listed as quabassiph)
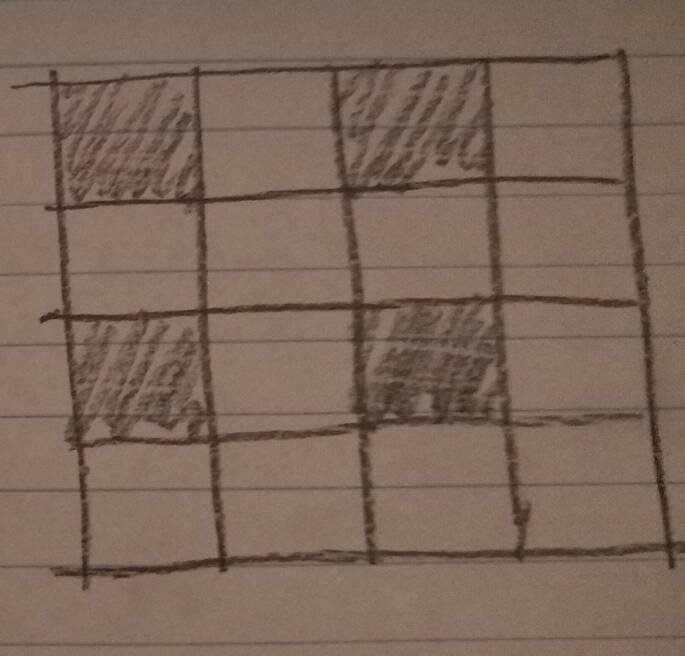
Blend 1/4 of the squares in squat, but shifted on alternate layers (a new member of the chon regiment!):
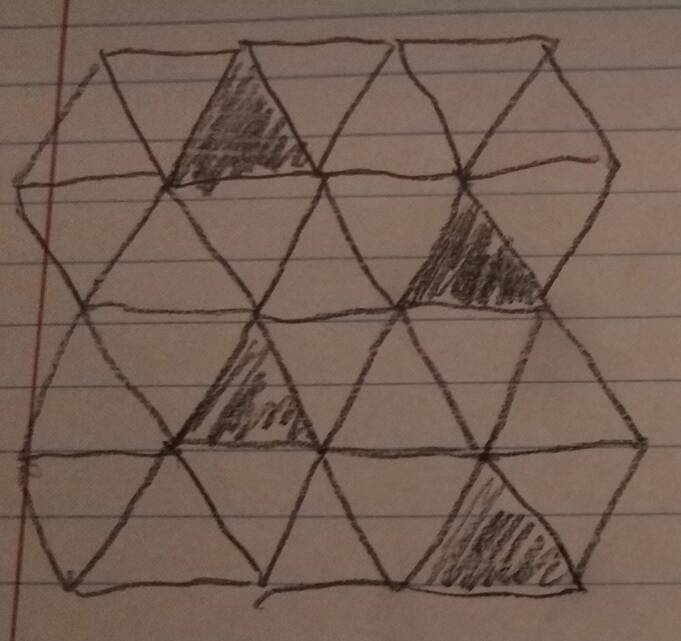
Blend 1/6 of the triangles in trat (e.g. the blue triangles in this picture of s3s3s3*a: https://commons.wikimedia.org/wiki/File ... 121314.png):
Blend 1/3 of the hexagons in hexat
Blend half the triangles in that
Blend the squares in tosquat
Blend half the octagons in tosquat
Blend the squares in quitsquat
Blend half the octagons in quitsquat
Blend the triangles in toxat
Blend the triangles in quothat
Blend the triangles in rothat
Blend the hexagons in rothat
Blend the triangles in shothat
Blend the hexagons in shothat
Blend the triangles in ghothat
Blend the hexagons in ghothat
Blend the triangles in qrothat
Blend the hexagons in qrothat
Blend the squares in sossa
Note: This and the next one are wild honeycombs because the pseudo-apeirogons in the middle of squats in the sossa pseudoprismatic honeycomb are intercepted by the ridge between two vertical azips.
Also, if we try to blend the apeirogons in any of these tilings' pseudoprismatic honeycombs, we end up with subdivisions with vertical rows of apeirogons instead of squats, so they would go in Category B (subdivisions) , not here.
Blend the squares in gossa
Blend the hexagons in shaha
Blend the hexagons in ghaha
Blend the squares in grothat
Blend the hexagons in grothat
Blend the dodecagons in grothat
Blend the octagons in satsa
Blend the octagrams in satsa
(If we blend the apeirogons it will just lead to a subdivided version of the satsa prismatic honeycomb, which will go into category B as before)
Blend the dodecagons in hatha
Blend the dodecagrams in hatha
Blend the octagons in qrasquit
Blend the octagrams in qrasquit
Blend the squares in qrasquit
Blend the dodecagons in thotithit
Blend the dodecagrams in thotithit
Blend the hexagons in thotithit
Blend the squares in quitothit
Blend the hexagons in quitothit
Blend the dodecagrams in quitothit
Blend half the squares in snasquat
Blend half the squares in rasisquat
Blend half the squares in snassa
Blend the non-snub triangles in snathat
Blend the hexagons in snathat
There may well be other blendings with snubs that I haven't investigated yet.
Each of these 43 selections of polygons from tilings corresponds to two honeycombs: one where the n-gonal apeirogonal duoprisms blend with the tiling's prismatic honeycomb, and another where the duoprisms are blended with tiling prisms which take up half the layers. Thus we have a total of 86 new uniform honeycombs.
First, prismatic honeycombs made from tilings containing n-gons can be blended with n-gonal apeirogonal duoprisms. However, no more than one of them can blend around each lateral edge of a prism (corresponding to a vertex in the original tiling). To find blendings that are uniform honeycombs, we need to find ways to color one type of face of a uniform tiling so that exactly one face around each vertex is colored and the tiling is still vertex transitive under the coloring.
I know of several ways to do this:
Blend 1/4 of the squares in squat (already listed as quabassiph)
Blend 1/4 of the squares in squat, but shifted on alternate layers (a new member of the chon regiment!):
Blend 1/6 of the triangles in trat (e.g. the blue triangles in this picture of s3s3s3*a: https://commons.wikimedia.org/wiki/File ... 121314.png):
Blend 1/3 of the hexagons in hexat
Blend half the triangles in that
Blend the squares in tosquat
Blend half the octagons in tosquat
Blend the squares in quitsquat
Blend half the octagons in quitsquat
Blend the triangles in toxat
Blend the triangles in quothat
Blend the triangles in rothat
Blend the hexagons in rothat
Blend the triangles in shothat
Blend the hexagons in shothat
Blend the triangles in ghothat
Blend the hexagons in ghothat
Blend the triangles in qrothat
Blend the hexagons in qrothat
Blend the squares in sossa
Note: This and the next one are wild honeycombs because the pseudo-apeirogons in the middle of squats in the sossa pseudoprismatic honeycomb are intercepted by the ridge between two vertical azips.
Also, if we try to blend the apeirogons in any of these tilings' pseudoprismatic honeycombs, we end up with subdivisions with vertical rows of apeirogons instead of squats, so they would go in Category B (subdivisions) , not here.
Blend the squares in gossa
Blend the hexagons in shaha
Blend the hexagons in ghaha
Blend the squares in grothat
Blend the hexagons in grothat
Blend the dodecagons in grothat
Blend the octagons in satsa
Blend the octagrams in satsa
(If we blend the apeirogons it will just lead to a subdivided version of the satsa prismatic honeycomb, which will go into category B as before)
Blend the dodecagons in hatha
Blend the dodecagrams in hatha
Blend the octagons in qrasquit
Blend the octagrams in qrasquit
Blend the squares in qrasquit
Blend the dodecagons in thotithit
Blend the dodecagrams in thotithit
Blend the hexagons in thotithit
Blend the squares in quitothit
Blend the hexagons in quitothit
Blend the dodecagrams in quitothit
Blend half the squares in snasquat
Blend half the squares in rasisquat
Blend half the squares in snassa
Blend the non-snub triangles in snathat
Blend the hexagons in snathat
There may well be other blendings with snubs that I haven't investigated yet.
Each of these 43 selections of polygons from tilings corresponds to two honeycombs: one where the n-gonal apeirogonal duoprisms blend with the tiling's prismatic honeycomb, and another where the duoprisms are blended with tiling prisms which take up half the layers. Thus we have a total of 86 new uniform honeycombs.
- Attachments
-
 trat-blend.jpg
trat-blend.jpg- (48.04 KiB) Not downloaded yet
-
 squat-blend-2.jpg
squat-blend-2.jpg- (40.13 KiB) Not downloaded yet
-
 squat-blend-1.jpg
squat-blend-1.jpg- (44.71 KiB) Not downloaded yet
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
I found some new uniform honeycombs that are blends of gacoca regiment members (square podium verf) with cuhsquah (thah verf).
First, a post by Mecejide on the Discord, mentioning a blend of squattip (square tiling prism) and gacoca, made me realize that edges can be added to gacoca between pairs of vertices one edge length apart, and the resulting edge skeleton is still vertex transitive.
I realized the same thing could be done in 2D with sossa. New edges can be added between vertices, perpendicular to the parallel sides in the trapezoid verf. At first, I didn't think it was possible to choose faces from this edge arrangement so that two faces met at an edge, but then I realized that sossa is still uniform when the two octagrams around each vertex have different colors. Blending with sha at the apeirogons worked because one set of octagrams got prograde squares as neighbors and the other set got retrograde squares. We can also blend sha with gossa. We can also facet subsymmetric sossa into a compound of two satsa, one at each vertex, which is in a sub-regiment (it has three out of the four edges of sossa around each vertex). There are two ways to blend 2-satsa with sha, one where octagrams touch prograde squares and the other where they touch retrograde squares.
Anyway, I found that these four tilings were already known. They are listed as rassersa, rarsisresa, rosassa, and rorisassa on Klitzing's site, and as irstobsint, irocsint, sirostobint, and girostobint on hsaka's site (I don't know what these acronyms stand for).
Then I realized that you could do the same thing in 3D with gacoca! Color the two sets of goccoes in gacoca different colors so that they cycle between two colors around each vertex. This gives a Wythoffian construction with octet symmetry. The squats in gocco come in sets exactly one edge length apart, so we can connect them with edges and blend with cuhsquah, which has cubes in alternate positions of the cubic honeycomb. Goccoes of one color (red) are adjacent to retrograde cubes, while goccoes of the other color (blue) are adjacent to prograde cubes. I think this works because the red and blue goccoes in gacoca swap places when we travel to a vertex in an adjacent square tiling one edge length away, and the cubes of cuhsquah do the same. The entire blend has octet symmetry.
Note that the stabilizers of the cubes in this blend have square pyramidal symmetry, so it is not kaleidoscopical unlike sabbadipady.
This construction should be possible with any member of the gacoca regiment with squats, as long as it has no faces from the sossa regiment. The half-symmetric gocco members can blend in two different ways. If I'm not mistaken, this should lead to 20 new uniform honeycombs.
Here's the verf of the blend of gacoca and cuhsquah.
First, a post by Mecejide on the Discord, mentioning a blend of squattip (square tiling prism) and gacoca, made me realize that edges can be added to gacoca between pairs of vertices one edge length apart, and the resulting edge skeleton is still vertex transitive.
I realized the same thing could be done in 2D with sossa. New edges can be added between vertices, perpendicular to the parallel sides in the trapezoid verf. At first, I didn't think it was possible to choose faces from this edge arrangement so that two faces met at an edge, but then I realized that sossa is still uniform when the two octagrams around each vertex have different colors. Blending with sha at the apeirogons worked because one set of octagrams got prograde squares as neighbors and the other set got retrograde squares. We can also blend sha with gossa. We can also facet subsymmetric sossa into a compound of two satsa, one at each vertex, which is in a sub-regiment (it has three out of the four edges of sossa around each vertex). There are two ways to blend 2-satsa with sha, one where octagrams touch prograde squares and the other where they touch retrograde squares.
Anyway, I found that these four tilings were already known. They are listed as rassersa, rarsisresa, rosassa, and rorisassa on Klitzing's site, and as irstobsint, irocsint, sirostobint, and girostobint on hsaka's site (I don't know what these acronyms stand for).
Then I realized that you could do the same thing in 3D with gacoca! Color the two sets of goccoes in gacoca different colors so that they cycle between two colors around each vertex. This gives a Wythoffian construction with octet symmetry. The squats in gocco come in sets exactly one edge length apart, so we can connect them with edges and blend with cuhsquah, which has cubes in alternate positions of the cubic honeycomb. Goccoes of one color (red) are adjacent to retrograde cubes, while goccoes of the other color (blue) are adjacent to prograde cubes. I think this works because the red and blue goccoes in gacoca swap places when we travel to a vertex in an adjacent square tiling one edge length away, and the cubes of cuhsquah do the same. The entire blend has octet symmetry.
Note that the stabilizers of the cubes in this blend have square pyramidal symmetry, so it is not kaleidoscopical unlike sabbadipady.
This construction should be possible with any member of the gacoca regiment with squats, as long as it has no faces from the sossa regiment. The half-symmetric gocco members can blend in two different ways. If I'm not mistaken, this should lead to 20 new uniform honeycombs.
Here's the verf of the blend of gacoca and cuhsquah.
Last edited by polychoronlover on Tue Jan 04, 2022 7:44 pm, edited 1 time in total.
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
I just started webpages for uniform tilings and uniform tetracombs on the first anniversary of my uniform honeycomb website:
https://ericbinnendyk.github.io/website/tilings.html
https://ericbinnendyk.github.io/website/tetracombs.html
https://ericbinnendyk.github.io/website/tilings.html
https://ericbinnendyk.github.io/website/tetracombs.html
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
Re: List of uniform honeycombs
I recently realized that any conjugate pair of expanded hypercube troop and contracted hypercube troop can tile Euclidean space together, even if they’re iquipadah types.
- Mecejide
- Trionian
- Posts: 86
- Joined: Sun Mar 10, 2019 1:58 am
- Location: Nethlekempt Farrows
Re: List of uniform honeycombs
Here's a Python program that I worked on in 2017-2019 to search the spict (small prismated icositetrachoric tetracomb) regiment (I made similar searchers to clear out some uniform honeycomb regiments such as octet, gacoca, and rich). I haven't had time to work on it in the past few years because real life (and other recreational projects) got in the way. I didn't want to post it until it was complete, but regiment searching is in style again now and there are other programs made by members of the Discord to search regiments too.
The potential facet regiments in the spict regiment (that I know of) are spic, ico, ope, triddip, tich, cont, proh, srit, srico, srich, sircope, and prich, but I never added sircope, prich, or gico from the ico regiment because I only realized they could occur after I was too busy to update my program. My program also can't currently eliminate IRCs, fissaries, or compounds.
Here is my program (Python 2):
Here is the list of 243 spict regiment members my program found. I suspect the actual count is below 200 after defissing.
The potential facet regiments in the spict regiment (that I know of) are spic, ico, ope, triddip, tich, cont, proh, srit, srico, srich, sircope, and prich, but I never added sircope, prich, or gico from the ico regiment because I only realized they could occur after I was too busy to update my program. My program also can't currently eliminate IRCs, fissaries, or compounds.
Here is my program (Python 2):
- Code: Select all
add = lambda x, y: x + y
# --RIDGE ORDERING IN EACH RIDGE REGIMENT--
# oct2 regiment: [none, oct2, thah1 (trigons on edge), thah2 (trigons in middle)]
# sirco1 regiment: [none, sirco1, socco1, sroh1]
# sirco2 regiment: [none, sirco2, socco2, sroh2]
# co1 regiment: [none, co1, oho1, cho1]
# --LOCAL RIDGE REGIMENT LISTS--
# spic regiment: [oct1, oct3, trip1, trip2, tic1, tic2, sirco1, sirco2]
# ico regiment: [oct1, oct2, co1]
# ope regiment: [oct2, trip1, trip3, cube]
# triddip regiment: [trip2, trip3]
# tich regiment: [oct2, tic1, tic3, tosquat]
# cont regiment: [tic2, tic3]
# proh regiment: [co1, trip1, tic1, op, girco]
# srit regiment: [oct2, trip3, tic3, sirco1, op]
# srico regiment: [co2, trip3, tic3, sirco2, girco]
# srich regiment: [co1, cube, tosquat, sirco1, girco]
# --FACET REGIMENT LIST--
# [spic, ico, ope, triddip, tich, cont, proh, srit, srico, srich]
# --GLOBAL RIDGE REGIMENT LIST--
# [oct1, oct2, oct3, trip1, trip2, trip3, tic1, tic2, tic3, sirco1, sirco2, cube, tosquat, co1, co2, op, girco]
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
# oct1 is on top (attached to ico), trip1 and tic1 point down, sirco1 is wider at bottom, oct2 is on sides
# co1 goes from top back to bottom front, co2 goes side to side
# trip3 and tic3 are on sides
# ipi1, inpac1, etc. are in the orientation on Bowers' website
# --FACET ORDERING IN EACH FACET REGIMENT--
facetlist = [[('spic', [1, 1, 1, 1, 0, 0, 0, 0]),
('siddic', [1, 1, 0, 0, 1, 1, 0, 0]),
('sripic', [0, 0, 1, 1, 1, 1, 0, 0]),
('smiffadic', [1, 1, 0, 0, 0, 0, 1, 1]),
('offadac', [0, 0, 0, 0, 1, 1, 1, 1]),
('sandic', [1, 1, 0, 0, 0, 0, 2, 2]),
('lifpic', [0, 0, 1, 1, 0, 0, 2, 2]),
('sirc', [0, 0, 0, 0, 0, 0, 3, 3]),
('ipi1', [0, 0, 1, 0, 0, 0, 1, 0]),
('inpac1', [1, 1, 1, 0, 0, 0, 0, 1]),
('picni1', [0, 0, 1, 0, 1, 1, 0, 1]),
('ridi1', [0, 0, 0, 0, 1, 0, 2, 0]),
('irnic1', [1, 1, 0, 0, 0, 1, 2, 0]),
('dipdi1', [0, 0, 1, 1, 1, 0, 0, 2]),
('sarnipadi1', [0, 0, 0, 1, 0, 1, 3, 0]),
('dirpidic1', [1, 1, 1, 0, 0, 1, 0, 3]),
('pifficdi1', [1, 1, 1, 0, 0, 1, 3, 0]),
('dinpi1', [0, 0, 0, 1, 1, 0, 1, 2]),
('dinic1', [1, 1, 0, 0, 0, 1, 1, 3]),
('inpic1', [1, 1, 1, 0, 0, 0, 3, 2]),
('ipi2', [0, 0, 0, 1, 0, 0, 0, 1]),
('inpac2', [1, 1, 0, 1, 0, 0, 1, 0]),
('picni2', [0, 0, 0, 1, 1, 1, 1, 0]),
('ridi2', [0, 0, 0, 0, 0, 1, 0, 2]),
('irnic2', [1, 1, 0, 0, 1, 0, 0, 2]),
('dipdi2', [0, 0, 1, 1, 0, 1, 2, 0]),
('sarnipadi2', [0, 0, 1, 0, 1, 0, 0, 3]),
('dirpidic2', [1, 1, 0, 1, 1, 0, 3, 0]),
('pifficdi2', [1, 1, 0, 1, 1, 0, 0, 3]),
('dinpi2', [0, 0, 1, 0, 0, 1, 2, 1]),
('dinic2', [1, 1, 0, 0, 1, 0, 3, 1]),
('inpic2', [1, 1, 0, 1, 0, 0, 2, 3])],
[('ico', [1, 1, 0]),
('oh', [1, 0, 2]),
('shahoh', [0, 1, 2]),
('huhoh', [0, 3, 3]),
('hohoh', [1, 2, 3]),
('ohuhoh', [1, 3, 1]),
('ghahoh', [0, 2, 1])],
[('ope', [1, 1, 1, 0]),
('thahp1', [2, 1, 0, 1]),
('thahp2', [3, 0, 1, 1])],
[('triddip', [1, 1])],
[('tich', [1, 1, 1, 0]),
('ticuhsquah1', [2, 1, 0, 1]),
('ticuhsquah2', [3, 0, 1, 1])],
[('cont', [1, 1])],
[('proh', [1, 1, 1, 1, 0]),
('siphado', [2, 1, 1, 0, 1]),
('sirpith', [3, 0, 0, 1, 1])],
[('srit', [1, 1, 0, 1, 0]),
('rawvatoth', [1, 0, 1, 2, 0]),
('sirdo', [0, 1, 1, 3, 0]),
('spript', [0, 1, 1, 0, 1]),
('garpit', [0, 0, 0, 3, 1]),
('pattinoth', [1, 0, 1, 1, 1]),
('pinpith', [1, 1, 0, 2, 1])],
[('srico', [1, 1, 0, 1, 0]),
('rawvaty', [1, 0, 1, 2, 0]),
('sirdi', [0, 1, 1, 3, 0]),
('spirdy', [0, 1, 1, 0, 1]),
('gardi', [0, 0, 0, 3, 1]),
('dindi', [1, 0, 1, 1, 1]),
('inipdi', [1, 1, 0, 2, 1])],
[('srich', [1, 1, 0, 1, 0]),
('rawvicoca', [1, 0, 1, 2, 0]),
('srich_3rd', [0, 1, 1, 3, 0]),
('srich_4th', [0, 1, 1, 0, 1]),
('srich_5th', [0, 0, 0, 3, 1]),
('srich_6th', [1, 0, 1, 1, 1]),
('srich_7th', [1, 1, 0, 2, 1])]]
# conversion from local ridge regiments to global ridge regiments
mappings = [[0, 2, 3, 4, 6, 7, 9, 10], [0, 1, 13], [1, 3, 5, 11], [4, 5], [1, 6, 8, 12], [7, 8], [13, 3, 6, 15, 16], [1, 5, 8, 9, 15], [14, 5, 8, 10, 16], [13, 11, 12, 9, 16]]
# number of times (once or twice) each ridge regiment of each facet contributes to touching the ridge (2 if identical facets meet at the ridge, otherwise 1)
incedences = [[1, 2, 1, 1, 1, 1, 1, 1], [1, 1, 1], [1, 1, 1, 1], [1, 1], [1, 1, 1, 1], [1, 1], [2, 1, 1, 1, 1], [1, 1, 1, 1, 1], [2, 1, 1, 1, 1], [1, 1, 1, 1, 1]]
flistlen = len(facetlist)
numrids = 17
def all0or2(lis):
zeroortwo = lambda x: x == 0 or x == 2
return all(map(zeroortwo, lis))
def somemorethan2(lis):
morethantwo = lambda x: x > 2
return any(map(morethantwo, lis))
# Increments the current facet configuration (facets) to the next possible configuration, e.g. [0, 0, 0, 0, 0, 0, 0, 3, 0, 7] -> [0, 0, 0, 0, 0, 0, 0, 3, 1, 0]. Only increments the sublist [0:last + 1]
def increment(lis, last):
if last == -1:
lis = [0] * flistlen
return
# It's supposed to be len(facetlist[last]) (not len(facetlist[last]) - 1) because we can have 0 (no regiment member) at the beginning.
if lis[last] == len(facetlist[last]):
lis[last] = 0
increment(lis, last - 1)
return
lis[last] += 1
def lastnotzero(lis):
if lis[-1] != 0:
return len(lis) - 1
else:
return lastnotzero(lis[:-1])
def globalize_ridgelist(ridgelist, find):
g_ridgelist = [0] * numrids
for local_rind, rid in enumerate(ridgelist):
g_ridgelist[mappings[find][local_rind]] = rid
return g_ridgelist
def global_incedences(ridgelist, find):
g_incedences = [0] * numrids
for local_rind, rid in enumerate(ridgelist):
if rid != 0:
g_incedences[mappings[find][local_rind]] = incedences[find][local_rind]
return g_incedences
def facetstoridges(facs):
rids = [0] * numrids
for find, fac in enumerate(facs):
# add ridges contributed by each facet
if fac > len(facetlist[find]):
# I'm confident enough in my code that I know I'll never reach this case and should probably remove it
print "Oh no!!! Facet list has a term out of bounds of facet regiment!"
rids = [0] * numrids
return
if fac > 0 and fac <= len(facetlist[find]):
# to do: deal with cases of clashing between different regiment members in ridge
rids = map(add, global_incedences(facetlist[find][fac - 1][1], find), rids)
return rids
ERR_CLASH = -1
# for a configuration of facets, fills the empty list (ridge list) with the number of each ridge regiment member achieved.
# returns ERR_CLASH (-1) if the same ridge achieves two regiment members (a clash)
def which_ridge_from_each_reg(facs, empty_list):
assert empty_list == [0] * numrids
# empty_list is an accumulation of the ridges contributed by each facet
for find, fac in enumerate(facs):
if fac > 0 and fac <= len(facetlist[find]):
which_rids = globalize_ridgelist(facetlist[find][fac - 1][1], find)
# combine ridges of this facet with ridges of previous facets
for i in range(numrids):
if which_rids[i] != 0:
if empty_list[i] == 0:
# adds ridge from new regiment
empty_list[i] = which_rids[i]
elif empty_list[i] == which_rids[i]:
# connects to the same regiment member
pass
else:
# attempts to connect two different regiment members - clash!
return ERR_CLASH
return 0
def facetnames(facets, isunique):
fstr = ''
for find, x in enumerate(facets):
if x > 0:
fstr += (facetlist[find][x - 1][0] + ' ')
find += 1
if (not isunique):
fstr += "(not unique)"
return fstr
'''def incr_search():
facets = [0] * flistlen
ridgelist = [0] * numrids
members = [] # List of facet lists (that actually connect properly)
while True:
if somemorethan2(ridgelist):
increment(facets, lastnotzero(facets))
else:
increment(facets, flistlen - 1)
if facets == [0] * flistlen:
return
ridgelist = facetstoridges(facets)
if all0or2(ridgelist):
isunique = True # add a verification only if the verf has some symmetry that is not needed for the facetings
if isunique:
members.append(facets)
print facetnames(facets, isunique)'''
# Revamping of above code
facets = [0] * flistlen
members = []
def incr_count(facets, start):
# precondition: facets[i] == 0 for all i >= start
for fac in range(len(facetlist[start]) + 1):
facets[start] = fac
ridgelist = facetstoridges(facets)
# no need to check this if fac == 0; it will have been detected by previous recursive layer of function
if fac != 0:
if max(ridgelist) > 2:
continue
# check for clashes between different members of ridge regiment
which_ridges = [0] * numrids
if which_ridge_from_each_reg(facets, which_ridges) == ERR_CLASH:
continue
if start < len(facets) - 1:
incr_count(facets, start + 1)
else:
# we have a complete set of facets, now convert to ridges
ridgelist = facetstoridges(facets)
if all0or2(ridgelist):
isunique = True # this would be the place where we check for duplicates of subsymmetric regiment members, but that doesn't apply to spict
if isunique:
members.append(facets)
print facetnames(facets, isunique)
facets[start] = 0
# postcondition: facets[i] == 0 for all i >= start
incr_count(facets, 0)
#flist_test = [9, 0, 1, 0, 0, 0, 0, 1, 0, 0] # blend of srittits
#print facetstoridges(flist_test)
Here is the list of 243 spict regiment members my program found. I suspect the actual count is below 200 after defissing.
- Code: Select all
sirdo spirdy srich_5th
sirpith spript spirdy
sirpith garpit srich_5th
ope tich proh spript
ope tich proh garpit spirdy srich_5th
ope tich siphado spirdy
ope tich siphado sirdo srich_5th
thahp1 ticuhsquah1 proh spript spirdy srich_4th
thahp1 ticuhsquah1 proh garpit srich_3rd
thahp1 ticuhsquah1 siphado srich_4th
thahp1 ticuhsquah1 siphado sirdo spirdy srich_3rd
thahp2 ticuhsquah2 spirdy srich_4th
thahp2 ticuhsquah2 sirdo srich_3rd
thahp2 ticuhsquah2 sirpith spript srich_4th
thahp2 ticuhsquah2 sirpith garpit spirdy srich_3rd
spic ico triddip tich proh spript
spic ico triddip tich proh garpit spirdy srich_5th
spic ico triddip tich siphado spirdy
spic ico triddip tich siphado sirdo srich_5th
spic ico ope triddip
spic ico ope triddip sirpith garpit srich_5th
siddic ico tich cont
siddic ico tich cont sirpith garpit srich_5th
siddic ico ope cont proh spript
siddic ico ope cont proh garpit spirdy srich_5th
siddic ico ope cont siphado spirdy
siddic ico ope cont siphado sirdo srich_5th
sripic triddip cont proh spript
sripic triddip cont proh garpit spirdy srich_5th
sripic triddip cont siphado spirdy
sripic triddip cont siphado sirdo srich_5th
sripic ope triddip tich cont
sripic ope triddip tich cont sirpith garpit srich_5th
sripic thahp1 triddip ticuhsquah1 cont spirdy srich_4th
sripic thahp1 triddip ticuhsquah1 cont sirdo srich_3rd
sripic thahp1 triddip ticuhsquah1 cont sirpith spript srich_4th
sripic thahp1 triddip ticuhsquah1 cont sirpith garpit spirdy srich_3rd
sripic thahp2 triddip ticuhsquah2 cont proh garpit srich_3rd
sripic thahp2 triddip ticuhsquah2 cont siphado srich_4th
smiffadic ico srit srico
smiffadic ico sirpith pattinoth dindi
smiffadic ohuhoh ticuhsquah2 dindi srich_6th
smiffadic ohuhoh thahp2 srico srich
offadac tich cont srit srico
offadac ope cont proh pattinoth srico
offadac ope cont siphado srit dindi
offadac ghahoh ticuhsquah1 cont dindi srich_6th
sandic ico rawvatoth rawvaty
sandic ico sirpith pinpith inipdi
sandic ohuhoh ticuhsquah2 rawvaty rawvicoca
sandic ohuhoh thahp2 inipdi srich_7th
lifpic triddip tich proh pinpith rawvaty
lifpic triddip tich siphado rawvatoth inipdi
lifpic ope triddip rawvatoth rawvaty
lifpic ghahoh thahp1 triddip inipdi srich_7th
sirc gardi srich_5th
sirc sirdo sirdi
sirc sirpith spript sirdi srich_5th
sirc sirpith garpit gardi
sirc ope tich proh spript gardi srich_5th
sirc ope tich proh garpit sirdi
sirc ope tich siphado sirdi srich_5th
sirc ope tich siphado sirdo gardi
sirc thahp1 ticuhsquah1 proh spript sirdi srich_3rd
sirc thahp1 ticuhsquah1 proh garpit gardi srich_4th
sirc thahp1 ticuhsquah1 siphado gardi srich_3rd
sirc thahp1 ticuhsquah1 siphado sirdo sirdi srich_4th
sirc thahp2 ticuhsquah2 sirdi srich_3rd
sirc thahp2 ticuhsquah2 sirdo gardi srich_4th
sirc thahp2 ticuhsquah2 sirpith spript gardi srich_3rd
sirc thahp2 ticuhsquah2 sirpith garpit sirdi srich_4th
ipi1 tich proh pattinoth
ipi1 tich siphado srit spirdy
ipi1 ope srit
ipi1 ope sirpith pattinoth spirdy
ipi1 ghahoh thahp1 srich
inpac1 ico tich proh spript srico
inpac1 ico tich proh garpit dindi srich_5th
inpac1 ico tich siphado dindi
inpac1 ico tich siphado sirdo srico srich_5th
inpac1 ico ope srico
inpac1 ico ope sirdo dindi srich_5th
inpac1 ico ope sirpith spript dindi
inpac1 ico ope sirpith garpit srico srich_5th
picni1 cont proh spript srico
picni1 cont proh garpit dindi srich_5th
picni1 cont siphado dindi
picni1 cont siphado sirdo srico srich_5th
picni1 ope tich cont srico
picni1 ope tich cont sirpith garpit srico srich_5th
picni1 thahp1 ticuhsquah1 cont dindi srich_4th
picni1 thahp1 ticuhsquah1 cont sirdo srico srich_3rd
picni1 thahp1 ticuhsquah1 cont sirpith spript srico srich_4th
picni1 thahp1 ticuhsquah1 cont sirpith garpit dindi srich_3rd
picni1 thahp2 ticuhsquah2 cont proh garpit srico srich_3rd
picni1 thahp2 ticuhsquah2 cont siphado srico srich_4th
ridi1 tich rawvatoth
ridi1 tich sirpith pinpith spirdy
ridi1 ope proh pinpith
ridi1 ope siphado rawvatoth spirdy
ridi1 ghahoh ticuhsquah1 rawvicoca
irnic1 ico cont rawvatoth
irnic1 ico cont sirpith pinpith spirdy
irnic1 ohuhoh ticuhsquah2 cont rawvicoca
irnic1 ohuhoh thahp2 cont spirdy srich_7th
dipdi1 triddip proh spript rawvaty
dipdi1 triddip proh garpit inipdi srich_5th
dipdi1 triddip siphado inipdi
dipdi1 triddip siphado sirdo rawvaty srich_5th
dipdi1 ope triddip tich rawvaty
dipdi1 ope triddip tich sirpith garpit rawvaty srich_5th
dipdi1 thahp1 triddip ticuhsquah1 inipdi srich_4th
dipdi1 thahp1 triddip ticuhsquah1 sirdo rawvaty srich_3rd
dipdi1 thahp1 triddip ticuhsquah1 sirpith spript rawvaty srich_4th
dipdi1 thahp1 triddip ticuhsquah1 sirpith garpit inipdi srich_3rd
dipdi1 thahp2 triddip ticuhsquah2 proh garpit rawvaty srich_3rd
dipdi1 thahp2 triddip ticuhsquah2 siphado rawvaty srich_4th
sarnipadi1 triddip cont spirdy srich_5th
sarnipadi1 triddip cont sirdo
sarnipadi1 triddip cont sirpith spript srich_5th
sarnipadi1 triddip cont sirpith garpit spirdy
sarnipadi1 ope triddip tich cont proh garpit
sarnipadi1 ope triddip tich cont siphado srich_5th
sarnipadi1 thahp1 triddip ticuhsquah1 cont proh spript srich_3rd
sarnipadi1 thahp1 triddip ticuhsquah1 cont proh garpit spirdy srich_4th
sarnipadi1 thahp1 triddip ticuhsquah1 cont siphado spirdy srich_3rd
sarnipadi1 thahp1 triddip ticuhsquah1 cont siphado sirdo srich_4th
sarnipadi1 thahp2 triddip ticuhsquah2 cont srich_3rd
sarnipadi1 thahp2 triddip ticuhsquah2 cont sirpith garpit srich_4th
dirpidic1 ico tich cont proh garpit gardi srich_5th
dirpidic1 ico tich cont siphado gardi
dirpidic1 ico ope cont sirdi
dirpidic1 ico ope cont sirdo gardi srich_5th
dirpidic1 ico ope cont sirpith spript gardi
dirpidic1 ico ope cont sirpith garpit sirdi srich_5th
pifficdi1 ico tich cont proh garpit
pifficdi1 ico tich cont siphado srich_5th
pifficdi1 ico ope cont spirdy srich_5th
pifficdi1 ico ope cont sirdo
pifficdi1 ico ope cont sirpith spript srich_5th
pifficdi1 ico ope cont sirpith garpit spirdy
dinpi1 triddip tich srit rawvaty
dinpi1 triddip tich sirpith pattinoth inipdi
dinpi1 ope triddip proh pattinoth rawvaty
dinpi1 ghahoh triddip ticuhsquah1 inipdi srich_6th
dinic1 ico cont srit sirdi
dinic1 ico cont sirpith pattinoth gardi
dinic1 ohuhoh ticuhsquah2 cont gardi srich_6th
dinic1 ohuhoh thahp2 cont sirdi srich
inpic1 ico tich proh spript inipdi srich_5th
inpic1 ico tich proh garpit rawvaty
inpic1 ico tich siphado rawvaty srich_5th
inpic1 ico tich siphado sirdo inipdi
inpic1 ico ope inipdi srich_5th
inpic1 ico ope sirdo rawvaty
inpic1 ico ope sirpith spript rawvaty srich_5th
inpic1 ico ope sirpith garpit inipdi
ipi2 triddip srico
ipi2 triddip sirdo dindi srich_5th
ipi2 triddip sirpith spript dindi
ipi2 triddip sirpith garpit srico srich_5th
ipi2 ope triddip tich proh garpit dindi srich_5th
ipi2 ope triddip tich siphado dindi
ipi2 thahp1 triddip ticuhsquah1 proh spript dindi srich_4th
ipi2 thahp1 triddip ticuhsquah1 proh garpit srico srich_3rd
ipi2 thahp1 triddip ticuhsquah1 siphado srico srich_4th
ipi2 thahp1 triddip ticuhsquah1 siphado sirdo dindi srich_3rd
ipi2 thahp2 triddip ticuhsquah2 dindi srich_4th
ipi2 thahp2 triddip ticuhsquah2 sirpith garpit dindi srich_3rd
inpac2 ico triddip srit
inpac2 ico triddip sirpith pattinoth spirdy
inpac2 ohuhoh triddip ticuhsquah2 spirdy srich_6th
inpac2 ohuhoh thahp2 triddip srich
picni2 triddip tich cont srit
picni2 ope triddip cont proh pattinoth
picni2 ghahoh triddip ticuhsquah1 cont spirdy srich_6th
ridi2 cont rawvaty
ridi2 cont sirdo inipdi srich_5th
ridi2 cont sirpith spript inipdi
ridi2 cont sirpith garpit rawvaty srich_5th
ridi2 ope tich cont proh garpit inipdi srich_5th
ridi2 ope tich cont siphado inipdi
ridi2 thahp1 ticuhsquah1 cont proh spript inipdi srich_4th
ridi2 thahp1 ticuhsquah1 cont proh garpit rawvaty srich_3rd
ridi2 thahp1 ticuhsquah1 cont siphado rawvaty srich_4th
ridi2 thahp1 ticuhsquah1 cont siphado sirdo inipdi srich_3rd
ridi2 thahp2 ticuhsquah2 cont inipdi srich_4th
ridi2 thahp2 ticuhsquah2 cont sirpith garpit inipdi srich_3rd
irnic2 ico tich rawvaty
irnic2 ico tich sirdo inipdi srich_5th
irnic2 ico tich sirpith spript inipdi
irnic2 ico tich sirpith garpit rawvaty srich_5th
irnic2 ico ope proh spript rawvaty
irnic2 ico ope proh garpit inipdi srich_5th
irnic2 ico ope siphado inipdi
irnic2 ico ope siphado sirdo rawvaty srich_5th
dipdi2 triddip tich cont proh pinpith
dipdi2 ope triddip cont rawvatoth
dipdi2 ghahoh thahp1 triddip cont spirdy srich_7th
sarnipadi2 proh spript sirdi
sarnipadi2 proh garpit gardi srich_5th
sarnipadi2 siphado gardi
sarnipadi2 siphado sirdo sirdi srich_5th
sarnipadi2 ope tich sirdi
sarnipadi2 ope tich sirdo gardi srich_5th
sarnipadi2 ope tich sirpith spript gardi
sarnipadi2 ope tich sirpith garpit sirdi srich_5th
sarnipadi2 thahp1 ticuhsquah1 gardi srich_4th
sarnipadi2 thahp1 ticuhsquah1 sirdo sirdi srich_3rd
sarnipadi2 thahp1 ticuhsquah1 sirpith spript sirdi srich_4th
sarnipadi2 thahp1 ticuhsquah1 sirpith garpit gardi srich_3rd
sarnipadi2 thahp2 ticuhsquah2 proh spript gardi srich_4th
sarnipadi2 thahp2 ticuhsquah2 proh garpit sirdi srich_3rd
sarnipadi2 thahp2 ticuhsquah2 siphado sirdi srich_4th
sarnipadi2 thahp2 ticuhsquah2 siphado sirdo gardi srich_3rd
dirpidic2 ico triddip tich spirdy srich_5th
dirpidic2 ico triddip tich sirdo
dirpidic2 ico triddip tich sirpith spript srich_5th
dirpidic2 ico triddip tich sirpith garpit spirdy
dirpidic2 ico ope triddip proh garpit
dirpidic2 ico ope triddip siphado srich_5th
pifficdi2 ico triddip tich sirdi
pifficdi2 ico triddip tich sirdo gardi srich_5th
pifficdi2 ico triddip tich sirpith spript gardi
pifficdi2 ico triddip tich sirpith garpit sirdi srich_5th
pifficdi2 ico ope triddip proh garpit gardi srich_5th
pifficdi2 ico ope triddip siphado gardi
dinpi2 tich cont proh pinpith srico
dinpi2 ope cont rawvatoth srico
dinpi2 ope cont sirpith pinpith dindi
dinpi2 ghahoh thahp1 cont dindi srich_7th
dinic2 ico tich dindi srich_5th
dinic2 ico tich sirdo srico
dinic2 ico tich sirpith spript srico srich_5th
dinic2 ico tich sirpith garpit dindi
dinic2 ico ope proh spript dindi srich_5th
dinic2 ico ope proh garpit srico
dinic2 ico ope siphado srico srich_5th
dinic2 ico ope siphado sirdo dindi
inpic2 ico triddip rawvatoth sirdi
inpic2 ico triddip sirpith pinpith gardi
inpic2 ohuhoh triddip ticuhsquah2 sirdi rawvicoca
inpic2 ohuhoh thahp2 triddip gardi srich_7th
Climbing method and elemental naming scheme are good.
- polychoronlover
- Trionian
- Posts: 72
- Joined: Wed Feb 29, 2012 1:15 am
99 posts
• Page 4 of 4 • 1, 2, 3, 4
Who is online
Users browsing this forum: No registered users and 50 guests
