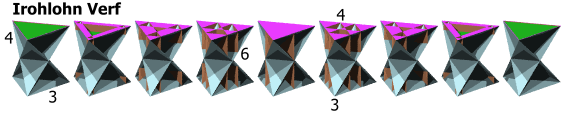
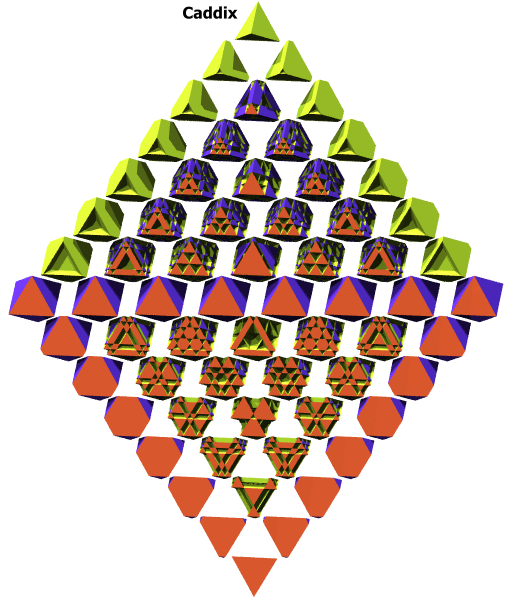
Polyhedron Dude wrote:... Chad - cellihemidodecateron. Its facets are 30 tepes (cyan and yellow) and 6 spids (red).
http://pages.suddenlink.net/hedrondude/chad.png
Matrix of its vertex figure (using the same vertex pattern as before):
- Code: Select all
8 | 3 3 | 3 9 | 4 3
--+-------+------+----
2 | 12 * | 2 2 | 2 2 ab x
2 | * 12 | 0 4 | 2 2 ae q
--+-------+------+----
3 | 3 0 | 8 * | 1 1 abc xxx verf(tet)
3 | 1 2 | * 24 | 1 1 abf xqq verf(trip)
--+-------+------+----
4 | 3 3 | 1 3 | 8 * abcf xo3oo&#q = verf(tepe)
6 | 6 6 | 2 6 | * 4 abcegh xo3ox&#q = verf(spid)
And thus of chad:
- Code: Select all
30 | 8 | 12 12 | 8 24 | 8 4
---+-----+--------+--------+-----
2 | 120 | 3 3 | 3 9 | 4 3
---+-----+--------+--------+-----
3 | 3 | 120 * | 2 2 | 2 2
4 | 4 | * 90 | 0 4 | 2 2
---+-----+--------+--------+-----
4 | 6 | 4 0 | 60 * | 1 1 (tet)
6 | 9 | 2 3 | * 120 | 1 1 (trip)
---+-----+--------+--------+-----
8 | 16 | 8 6 | 2 4 | 30 * (tepe)
20 | 60 | 40 30 | 10 20 | * 6 (spid)
--- rk



















 .
.



 .
.