- Code: Select all
x3o3o
o3o3x
o3o3o
o3x3o
o3o3o
I watch the list, there are plenty of pretty pictures, but time constraints etc limit me to what is mayly on the box.
x3o3o
o3o3x
o3o3o
o3x3o
o3o3o
wendy wrote:Is this thing in the list yet? It's the gosset polytope 1_21 in five dimensions or the same as the half-cube. The lace city for it follows. 2_11 is bleadingly obvious.
- Code: Select all
x3o3o
o3o3x
o3o3o
o3x3o
o3o3o
I watch the list, there are plenty of pretty pictures, but time constraints etc limit me to what is mayly on the box.
x3o3o *b3o3o
. . . . . | 16 | 10 | 30 | 10 20 | 5 5 verf=rap
-------------+----+----+-----+-------+------
x . . . . | 2 | 80 | 6 | 3 6 | 3 2 edge-fig.=trip
-------------+----+----+-----+-------+------
x3o . . . | 3 | 3 | 160 | 1 2 | 2 1
-------------+----+----+-----+-------+------
x3o3o . . | 4 | 6 | 4 | 40 * | 2 0 tet
x3o . *b3o . | 4 | 6 | 4 | * 80 | 1 1 tet
-------------+----+----+-----+-------+------
x3o3o *b3o . | 8 | 24 | 32 | 8 8 | 10 * hex
x3o . *b3o3o | 5 | 10 | 10 | 0 5 | * 16 penPolyhedron Dude wrote:... Quittin - quasitruncated penteract, or stellatruncated penteract. Its symbol is ooox"x, it is the 5-D version of quith. Interestingly, this one has holes in it due to its quitit facets having zero density regions inside. Facets are 10 quitits (lavender) and 32 pens (aqua).
http://pages.suddenlink.net/hedrondude/quittin.png ...
o3o3o3x4/3x
. . . . . | 160 | 4 1 | 6 4 | 4 6 | 1 4
------------+-----+--------+--------+--------+------
. . . x . | 2 | 320 * | 3 1 | 3 3 | 1 3
. . . . x | 2 | * 80 | 0 4 | 0 6 | 0 4 edge-fig.=tet
------------+-----+--------+--------+--------+------
. . o3x . | 3 | 3 0 | 320 * | 2 1 | 1 2
. . . x4/3x | 8 | 4 4 | * 80 | 0 3 | 0 3
------------+-----+--------+--------+--------+------
. o3o3x . | 4 | 6 0 | 4 0 | 160 * | 1 1 tet
. . o3x4/3x | 24 | 24 12 | 8 6 | * 40 | 0 2 quith
------------+-----+--------+--------+--------+------
o3o3o3x . | 5 | 10 0 | 10 0 | 5 0 | 32 * pen
. o3o3x4/3x | 64 | 96 32 | 64 24 | 16 8 | * 10 quititPolyhedron Dude wrote:... Gaqrin - great quasirhombated penteract. Its symbol is ooxx"x. Its facets are 10 gaqrits (blue), 32 tips (golden), and 80 tepes (red).
http://pages.suddenlink.net/hedrondude/gaqrin.png
o3o3x3x4x
. . . . . | 640 | 3 1 1 | 3 3 3 1 | 1 3 3 3 | 1 1 3
----------+-----+-------------+----------------+----------------+---------
. . x . . | 2 | 960 * * | 2 1 1 0 | 1 2 2 1 | 1 1 2
. . . x . | 2 | * 320 * | 0 3 0 1 | 0 3 0 3 | 1 0 3
. . . . x | 2 | * * 320 | 0 0 3 1 | 0 0 3 3 | 0 1 3
----------+-----+-------------+----------------+----------------+---------
. o3x . . | 3 | 3 0 0 | 640 * * * | 1 1 1 0 | 1 1 1
. . x3x . | 6 | 3 3 0 | * 320 * * | 0 2 0 1 | 1 0 2
. . x . x | 4 | 2 0 2 | * * 480 * | 0 0 2 1 | 0 1 2
. . . x4x | 8 | 0 4 4 | * * * 80 | 0 0 0 3 | 0 0 3
----------+-----+-------------+----------------+----------------+---------
o3o3x . . | 4 | 6 0 0 | 4 0 0 0 | 160 * * * | 1 1 0 tet
. o3x3x . | 12 | 12 6 0 | 4 4 0 0 | * 160 * * | 1 0 1 tut
. o3x . x | 6 | 6 0 3 | 2 0 3 0 | * * 320 * | 0 1 1 trip
. . x3x4x | 48 | 24 24 24 | 0 8 12 6 | * * * 40 | 0 0 2 girco
----------+-----+-------------+----------------+----------------+---------
o3o3x3x . | 20 | 30 10 0 | 20 10 0 0 | 5 5 0 0 | 32 * * tip
o3o3x . x | 8 | 6 0 4 | 8 0 6 0 | 2 0 4 0 | * 80 * tepe
. o3x3x4x | 192 | 192 96 96 | 64 64 96 24 | 0 16 32 8 | * * 10 grito3o3x3x4/3x
. . . . . | 640 | 3 1 1 | 3 3 3 1 | 1 3 3 3 | 1 1 3
------------+-----+-------------+----------------+----------------+---------
. . x . . | 2 | 960 * * | 2 1 1 0 | 1 2 2 1 | 1 1 2
. . . x . | 2 | * 320 * | 0 3 0 1 | 0 3 0 3 | 1 0 3
. . . . x | 2 | * * 320 | 0 0 3 1 | 0 0 3 3 | 0 1 3
------------+-----+-------------+----------------+----------------+---------
. o3x . . | 3 | 3 0 0 | 640 * * * | 1 1 1 0 | 1 1 1
. . x3x . | 6 | 3 3 0 | * 320 * * | 0 2 0 1 | 1 0 2
. . x . x | 4 | 2 0 2 | * * 480 * | 0 0 2 1 | 0 1 2
. . . x4/3x | 8 | 0 4 4 | * * * 80 | 0 0 0 3 | 0 0 3
------------+-----+-------------+----------------+----------------+---------
o3o3x . . | 4 | 6 0 0 | 4 0 0 0 | 160 * * * | 1 1 0 tet
. o3x3x . | 12 | 12 6 0 | 4 4 0 0 | * 160 * * | 1 0 1 tut
. o3x . x | 6 | 6 0 3 | 2 0 3 0 | * * 320 * | 0 1 1 trip
. . x3x4/3x | 48 | 24 24 24 | 0 8 12 6 | * * * 40 | 0 0 2 quitco
------------+-----+-------------+----------------+----------------+---------
o3o3x3x . | 20 | 30 10 0 | 20 10 0 0 | 5 5 0 0 | 32 * * tip
o3o3x . x | 8 | 6 0 4 | 8 0 6 0 | 2 0 4 0 | * 80 * tepe
. o3x3x4/3x | 192 | 192 96 96 | 64 64 96 24 | 0 16 32 8 | * * 10 gaqritwendy wrote:Is this thing in the list yet? It's the gosset polytope 1_21 in five dimensions or the same as the half-cube. The lace city for it follows. 2_11 is bleadingly obvious.
- Code: Select all
x3o3o
o3o3x
o3o3o
o3x3o
o3o3o
I watch the list, there are plenty of pretty pictures, but time constraints etc limit me to what is mayly on the box.


x3o3o *b3o3o
. . . . . | 16 | 10 | 30 | 10 20 | 5 5 verf=rap
-------------+----+----+-----+-------+------
x . . . . | 2 | 80 | 6 | 3 6 | 3 2 edge-fig.=trip
-------------+----+----+-----+-------+------
x3o . . . | 3 | 3 | 160 | 1 2 | 2 1
-------------+----+----+-----+-------+------
x3o3o . . | 4 | 6 | 4 | 40 * | 2 0 tet
x3o . *b3o . | 4 | 6 | 4 | * 80 | 1 1 tet
-------------+----+----+-----+-------+------
x3o3o *b3o . | 8 | 24 | 32 | 8 8 | 10 * hex
x3o . *b3o3o | 5 | 10 | 10 | 0 5 | * 16 pen

o3o3x3x4x
. . . . . | 640 | 3 1 1 | 3 3 3 1 | 1 3 3 3 | 1 1 3
----------+-----+-------------+----------------+----------------+---------
. . x . . | 2 | 960 * * | 2 1 1 0 | 1 2 2 1 | 1 1 2
. . . x . | 2 | * 320 * | 0 3 0 1 | 0 3 0 3 | 1 0 3
. . . . x | 2 | * * 320 | 0 0 3 1 | 0 0 3 3 | 0 1 3
----------+-----+-------------+----------------+----------------+---------
. o3x . . | 3 | 3 0 0 | 640 * * * | 1 1 1 0 | 1 1 1
. . x3x . | 6 | 3 3 0 | * 320 * * | 0 2 0 1 | 1 0 2
. . x . x | 4 | 2 0 2 | * * 480 * | 0 0 2 1 | 0 1 2
. . . x4x | 8 | 0 4 4 | * * * 80 | 0 0 0 3 | 0 0 3
----------+-----+-------------+----------------+----------------+---------
o3o3x . . | 4 | 6 0 0 | 4 0 0 0 | 160 * * * | 1 1 0 tet
. o3x3x . | 12 | 12 6 0 | 4 4 0 0 | * 160 * * | 1 0 1 tut
. o3x . x | 6 | 6 0 3 | 2 0 3 0 | * * 320 * | 0 1 1 trip
. . x3x4x | 48 | 24 24 24 | 0 8 12 6 | * * * 40 | 0 0 2 girco
----------+-----+-------------+----------------+----------------+---------
o3o3x3x . | 20 | 30 10 0 | 20 10 0 0 | 5 5 0 0 | 32 * * tip
o3o3x . x | 8 | 6 0 4 | 8 0 6 0 | 2 0 4 0 | * 80 * tepe
. o3x3x4x | 192 | 192 96 96 | 64 64 96 24 | 0 16 32 8 | * * 10 grit
 - got nothing to do ...
- got nothing to do ... 
Klitzing wrote::( - got nothing to do ...
--- rk
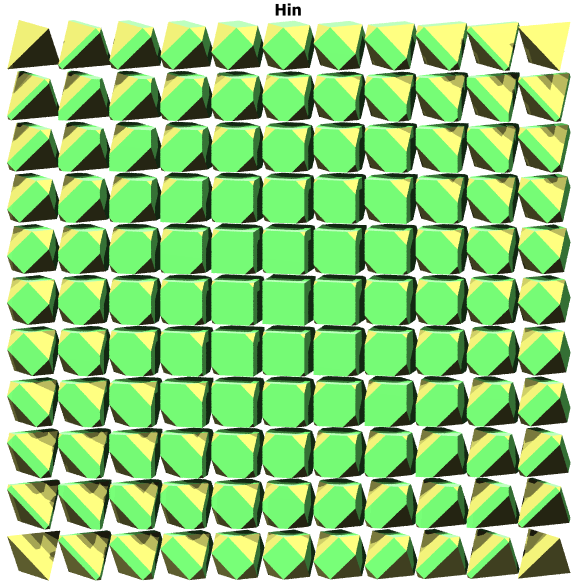
wendy wrote:The 'hin' section is rather interesting, as there is lots of activity going on in it. Wendy thanks Polyhedron Dude and Klitzing for the show.

 Recently I (re)found a very nice and quite useful formula!
Recently I (re)found a very nice and quite useful formula!
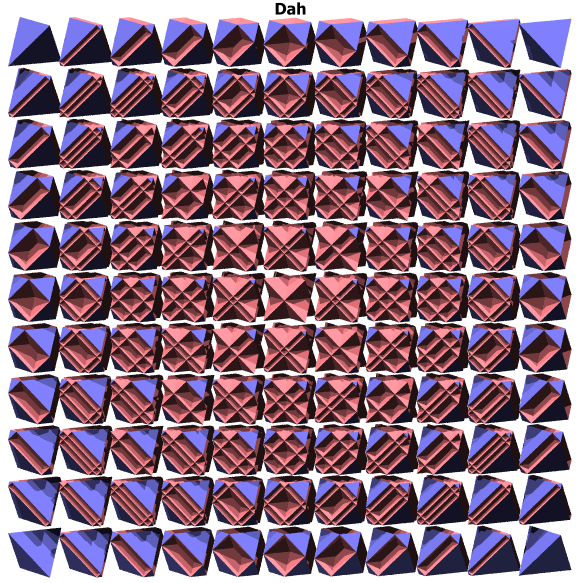



 ) - rinah and radah - coming soon!
) - rinah and radah - coming soon!Polyhedron Dude wrote:... Dah - dishexadecateron. It is a member of the hin regiment and its verf is a firp. It is semiregular. Its facets are 16 raps (pink) and 16 pens (blue).
http://pages.suddenlink.net/hedrondude/dah.png
...
16 | 10 | 30 | 20 15 | 5 10 verf=firp
---+----+-----+-------+------
2 | 80 | 6 | 6 6 | 2 6
---+----+-----+-------+------
3 | 3 | 160 | 2 2 | 1 3
---+----+-----+-------+------
4 | 6 | 4 | 80 * | 1 1 tet
6 | 12 | 8 | * 40 | 0 2 oct
---+----+-----+-------+------
5 | 10 | 10 | 5 0 | 16 * pen
10 | 30 | 30 | 5 5 | * 16 rapPolyhedron Dude wrote:... Han - hexadecapenteract. Also a member of the hin regiment, its verf is a pinnip and it is also semiregular. Its facets are 10 hexes (yellow) and 16 raps (blue grey).
http://pages.suddenlink.net/hedrondude/han.png
...
16 | 10 | 30 | 10 20 15 | 5 10 verf=pinnip
---+----+-----+----------+------
2 | 80 | 6 | 3 6 6 | 3 6
---+----+-----+----------+------
3 | 3 | 160 | 1 2 2 | 2 3
---+----+-----+----------+------
4 | 6 | 4 | 40 * * | 2 0 tet
4 | 6 | 4 | * 80 * | 1 1 tet
6 | 12 | 8 | * * 40 | 0 2 oct
---+----+-----+----------+------
8 | 24 | 32 | 8 8 0 | 10 * hex
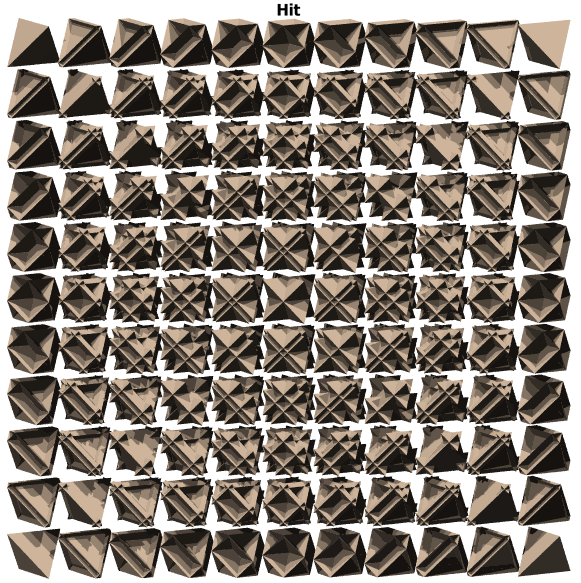
10 | 30 | 30 | 0 5 5 | * 16 rapPolyhedron Dude wrote:... Hit - hexadecateron. This is the noble member of the hin regiment. Its facets are 16 pinnips. I bet this one will be a hit!
http://pages.suddenlink.net/hedrondude/hit.png
The hin regiment has 2 more members to be revealed (even though they are on my polyteron website) - rinah and radah - coming soon!
16 | 10 | 30 !20 | 15 30 | 10
---+----+---------+-------+---
2 | 80 | 6 !4 | 6 9 | 6
---+----+---------+-------+---
3 | 3 | 160 * | 2 1 | 3
4 | 4 | * !80 | 0 !3 | !3
---+----+---------+-------+---
6 | 12 | 8 0 | 40 * | 2 oct
6 | 9 | 2 3 | * 80 | 2 trip
---+----+---------+-------+---
10 | 30 | 30 15 | 5 10 | 16 pinnip

Klitzing wrote:Polyhedron Dude wrote:... Hit - hexadecateron. This is the noble member of the hin regiment. Its facets are 16 pinnips. I bet this one will be a hit!
The hin regiment has 2 more members to be revealed (even though they are on my polyteron website) - rinah and radah - coming soon!
Incidence matrix ...
 Outch, got the number of squares wrong. (And therby some few derived numbers too.) One should don not make 2 steps by one...
Outch, got the number of squares wrong. (And therby some few derived numbers too.) One should don not make 2 steps by one...Vertex Pattern:
a g
b c h
e d i j
f
6 * | 4 1 2 2 0 | 2 4 6 4 1 | 4 2 a
* 4 | 0 0 3 3 3 | 0 6 3 3 3 | 3 3 g
----+--------------+--------------+----
2 0 | 12 * * * * | 1 1 1 0 0 | 2 1 ab x
2 0 | * 3 * * * | 0 0 0 4 0 | 4 0 af q
1 1 | * * 12 * * | 0 2 0 1 0 | 2 1 ag x
1 1 | * * * 12 * | 0 0 2 1 1 | 2 2 ai q
0 2 | * * * * 6 | 0 2 0 0 1 | 1 2 gh x
----+--------------+--------------+----
4 0 | 4 0 0 0 0 | 3 * * * * | 2 0 abfd xxxx = verf(oct)
2 2 | 1 0 2 0 1 | * 12 * * * | 1 1 abih xxxx = verf(oct)
2 1 | 1 0 0 2 0 | * * 12 * * | 1 1 abj xqq = verf(trip)
2 1 | 0 1 1 1 0 | * * * 12 * | 2 0 agf xqq = verf(trip)
1 2 | 0 0 0 2 1 | * * * * 6 | 0 2 aij xqq = verf(trip)
----+--------------+--------------+----
4 2 | 4 2 4 4 1 | 1 2 2 4 0 | 6 * abdfgj verf(pinnip)
3 3 | 3 0 3 6 3 | 0 3 3 0 3 | * 4 abchij verf(pinnip)
or
10 | 6 3 | 6 9 | 6
---+-------+-------+---
2 | 30 * | 2 1 | 3 x
2 | * 15 | 0 4 | 4 q
---+-------+-------+---
4 | 4 0 | 15 * | 2 verf(oct)
3 | 1 2 | * 30 | 2 verf(trip)
---+-------+-------+---
6 | 9 6 | 3 6 | 10 verf(pinnip)
16 | 10 | 30 15 | 15 30 | 10
---+----+--------+-------+---
2 | 80 | 6 3 | 6 9 | 6
---+----+--------+-------+---
3 | 3 | 160 * | 2 1 | 3
4 | 4 | * 60 | 0 4 | 4
---+----+--------+-------+---
6 | 12 | 8 0 | 40 * | 2 (oct)
6 | 9 | 2 3 | * 80 | 2 (trip)
---+----+--------+-------+---
10 | 30 | 30 15 | 5 10 | 16 (pinnip)
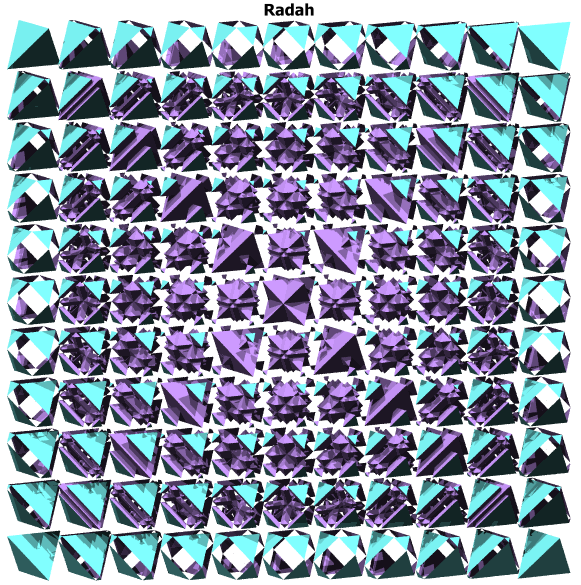
Polyhedron Dude wrote:... Radah - retrodishexadecateron - facets are 16 pens (cyan) and 16 firps (lavender). This one has a nice spiky look to it.
http://pages.suddenlink.net/hedrondude/radah.png
...
Vertex Pattern:
a g
b c h
e d i j
f
6 * | 4 1 2 2 0 | 2 4 4 4 1 0 | 4 2 2 0 a
* 4 | 0 0 3 3 3 | 0 3 3 3 3 3 | 3 3 1 1 g
----+--------------+----------------+--------
2 0 | 12 * * * * | 1 1 1 0 0 0 | 1 1 1 0 ab x
2 0 | * 3 * * * | 0 0 0 4 0 0 | 4 0 0 0 af q
1 1 | * * 12 * * | 0 2 0 1 0 0 | 2 0 1 0 ag x
1 1 | * * * 12 * | 0 0 2 1 1 0 | 2 2 0 0 ai q
0 2 | * * * * 6 | 0 0 0 0 1 2 | 0 2 0 1 gh x
----+--------------+----------------+--------
3 0 | 3 0 0 0 0 | 4 * * * * * | 0 1 1 0 abc xxx = verf(tet)
2 1 | 1 0 2 0 0 | * 12 * * * * | 1 0 1 0 abg xxx = verf(tet)
2 1 | 1 0 0 2 0 | * * 12 * * * | 1 1 0 0 abj xqq = verf(trip)
2 1 | 0 1 1 1 0 | * * * 12 * * | 2 0 0 0 afg xqq = verf(trip)
1 2 | 0 0 0 2 1 | * * * * 6 * | 0 2 0 0 aij xqq = verf(trip)
0 3 | 0 0 0 0 3 | * * * * * 4 | 0 1 0 1 ghi xxx = verf(tet)
----+--------------+----------------+--------
4 2 | 2 2 4 4 0 | 0 2 2 4 0 0 | 6 * * * abdfgj verf(firp)
3 3 | 3 0 0 6 3 | 1 0 3 0 3 1 | * 4 * * abchij verf(firp)
3 1 | 3 0 3 0 0 | 1 3 0 0 0 0 | * * 4 * abcg tet = verf(pen)
0 4 | 0 0 0 0 6 | 0 0 0 0 0 4 | * * * 1 ghij tet = verf(pen)
or
10 | 6 3 | 6 9 | 6 2
---+-------+-------+-----
2 | 30 * | 2 1 | 2 1 x
2 | * 15 | 0 4 | 4 0 q
---+-------+-------+-----
3 | 3 0 | 20 * | 1 1 xxx = verf(tet)
3 | 1 2 | * 30 | 2 0 xqq = verf(trip)
---+-------+-------+-----
6 | 6 6 | 2 6 | 10 * verf(firp)
4 | 6 0 | 4 0 | * 5 tet = verf(pen)
16 | 10 | 30 15 | 20 30 | 10 5
---+----+--------+-------+------
2 | 80 | 6 3 | 6 9 | 6 2
---+----+--------+-------+------
3 | 3 | 160 * | 2 1 | 2 1
4 | 4 | * 60 | 0 4 | 4 0
---+----+--------+-------+------
4 | 6 | 4 0 | 80 * | 1 1 tet
6 | 9 | 2 3 | * 80 | 2 0 trip
---+----+--------+-------+------
10 | 30 | 20 15 | 5 10 | 16 * firp
5 | 10 | 10 0 | 5 0 | * 16 pen
 )
)Polyhedron Dude wrote:Now for the final [two] member[s] of the hin regiment:
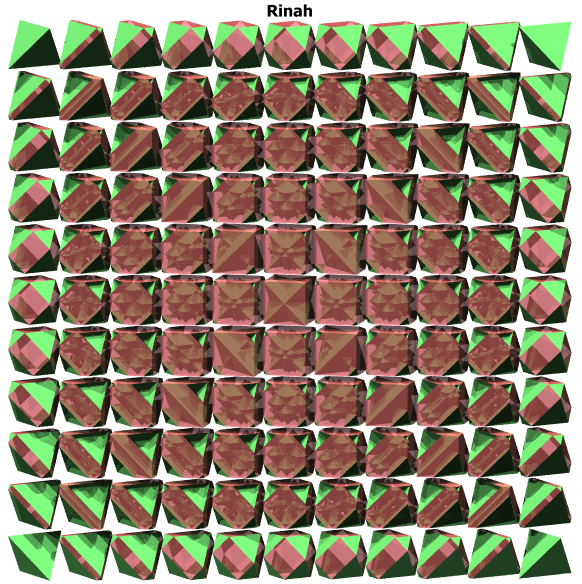
... Rinah - retropenteractihexadecateron - facets are 10 hexes (transparent red) and 16 firps (green). This one is a copycat to han and its only difference is its internal structure, so I rendered the hexes as transparent to get a glimpse inside.
http://pages.suddenlink.net/hedrondude/rinah.png
Vertex Pattern:
a g
b c h
e d i j
f
6 * | 4 1 2 2 0 | 2 2 4 4 4 1 1 0 | 1 4 2 2 a
* 4 | 0 0 3 3 3 | 0 0 3 3 3 3 3 3 | 0 3 3 3 g
----+--------------+--------------------+--------
2 0 | 12 * * * * | 1 1 1 1 0 0 0 0 | 1 1 1 1 ab x
2 0 | * 3 * * * | 0 0 0 0 4 0 0 0 | 0 4 0 0 af q
1 1 | * * 12 * * | 0 0 2 0 1 1 0 0 | 0 2 0 2 ag x
1 1 | * * * 12 * | 0 0 0 2 1 0 1 0 | 0 2 2 0 ai q
0 2 | * * * * 6 | 0 0 0 0 0 1 1 2 | 0 0 2 2 gh x
----+--------------+--------------------+--------
3 0 | 3 0 0 0 0 | 4 * * * * * * * | 1 0 1 0 abc xxx = verf(tet) hf
3 0 | 3 0 0 0 0 | * 4 * * * * * * | 1 0 0 1 abe xxx = verf(tet) hh
2 1 | 1 0 2 0 0 | * * 12 * * * * * | 0 1 0 1 abg xxx = verf(tet) hf
2 1 | 1 0 0 2 0 | * * * 12 * * * * | 0 1 1 0 abj xqq = verf(trip)
2 1 | 0 1 1 1 0 | * * * * 12 * * * | 0 2 0 0 afg xqq = verf(trip)
1 2 | 0 0 2 0 1 | * * * * * 6 * * | 0 0 0 2 agh xxx = verf(tet) hh
1 2 | 0 0 0 2 1 | * * * * * * 6 * | 0 0 2 0 aij xqq = verf(trip)
0 3 | 0 0 0 0 3 | * * * * * * * 4 | 0 0 1 1 ghi xxx = verf(tet) hf
----+--------------+--------------------+--------
6 0 | 12 0 0 0 0 | 4 4 0 0 0 0 0 0 | 1 * * * abcdef oct = verf(hex)
4 2 | 2 2 4 4 0 | 0 0 2 2 4 0 0 0 | * 6 * * abdfgj verf(firp)
3 3 | 3 0 0 6 3 | 1 0 0 3 0 0 3 1 | * * 4 * abchij verf(firp)
3 3 | 3 0 6 0 3 | 0 1 3 0 0 3 0 1 | * * * 4 abeghi oct = verf(hex)
or
10 | 6 3 | 3 6 9 | 3 6
---+-------+----------+-----
2 | 30 * | 1 2 1 | 2 2 x
2 | * 15 | 0 0 4 | 0 4 q
---+-------+----------+-----
3 | 3 0 | 10 * * | 2 0 xxx = verf(tet) hh
3 | 3 0 | * 20 * | 1 1 xxx = verf(tet) hf
3 | 1 2 | * * 30 | 0 2 xqq = verf(trip)
---+-------+----------+-----
6 | 12 0 | 4 4 0 | 5 * oct = verf(hex)
6 | 6 6 | 0 2 6 | * 10 verf(firp)16 | 10 | 30 15 | 10 20 30 | 5 10
---+----+--------+----------+------
2 | 80 | 6 3 | 3 6 9 | 3 6
---+----+--------+----------+------
3 | 3 | 160 * | 1 2 1 | 2 2
4 | 4 | * 60 | 0 0 4 | 0 4
---+----+--------+----------+------
4 | 6 | 4 0 | 40 * * | 2 0 tet
4 | 6 | 4 0 | * 80 * | 1 1 tet
6 | 9 | 2 3 | * * 80 | 0 2 trip
---+----+--------+----------+------
8 | 24 | 32 0 | 8 8 0 | 10 * hex
10 | 30 | 20 15 | 0 5 10 | * 16 firp
(copycat = same external surtope). This is quite evident from his field of sectionings, but else would be rather surprising. Han has for facets octs and trip, while rinah has for facets octs and firps. Sure, firp is a faceting of trip, but the prominent external squares would be missing. That is, han would hide those squares from external vision.This one is a copycat to han and its only difference is its internal structure





Polyhedron Dude wrote:Our next [two] polytera are from the nit regiment, notice how different they look:
Irl - invertiretrolepidoteron - its facets are 16 pinnips (red), 16 rawvtips (purple), and 16 sirdops (cyan).
http://pages.suddenlink.net/hedrondude/irl.png -- the url to irl...
Vertex Pattern:
a b g h
c i
d e j k
f l
12 | 2 1 2 2 | 2 3 3 2 2 | 1 3 3
---+------------+-------------+------
2 | 12 * * * | 1 1 1 0 0 | 1 1 1 ab x
2 | * 6 * * | 2 0 0 2 0 | 1 3 0 ag x
2 | * * 12 * | 0 2 0 0 1 | 1 0 2 ah q
2 | * * * 12 | 0 0 2 1 1 | 0 2 2 ak h
---+------------+-------------+------
4 | 2 2 0 0 | 6 * * * * | 1 1 0 abgh xxxx = verf(oct)
3 | 1 0 2 0 | * 12 * * * | 1 0 1 abi xqq = verf(trip)
3 | 1 0 0 2 | * * 12 * * | 0 1 1 abl xhh = verf(tut)
4 | 0 2 0 2 | * * * 6 * | 0 2 0 aegk xh(-x)h = verf(oho)
4 | 0 0 2 2 | * * * * 6 | 0 0 2 adhk qh(-q)h = verf(cho)
---+------------+-------------+------
6 | 6 3 6 0 | 3 6 0 0 0 | 2 * * abcghi verf(pinnip)
6 | 2 3 0 4 | 1 0 2 2 0 | * 6 * abfghl verf(rawvtip)
6 | 2 0 4 4 | 0 2 2 0 2 | * * 6 abdeil verf(sirdop)80 | 12 | 12 6 12 12 | 6 12 12 6 6 | 2 6 6
---+-----+-----------------+-----------------+---------
2 | 480 | 2 1 2 2 | 2 3 3 2 2 | 1 3 3
---+-----+-----------------+-----------------+---------
3 | 3 | 320 * * * | 1 1 1 0 0 | 1 1 1
3 | 3 | * 160 * * | 2 0 0 2 0 | 1 3 0
4 | 4 | * * 240 * | 0 2 0 0 1 | 1 0 2
6 | 6 | * * * 160 | 0 0 2 1 1 | 0 2 2
---+-----+-----------------+-----------------+---------
6 | 12 | 4 4 0 0 | 80 * * * * | 1 1 0 oct
6 | 9 | 2 0 3 0 | * 160 * * * | 1 0 1 trip
12 | 18 | 4 0 0 4 | * * 80 * * | 0 1 1 tut
12 | 24 | 0 8 0 4 | * * * 40 * | 0 2 0 oho
12 | 24 | 0 0 6 4 | * * * * 40 | 0 0 2 cho
---+-----+-----------------+-----------------+---------
10 | 30 | 20 10 15 0 | 5 10 0 0 0 | 16 * * pinnip
30 | 90 | 20 30 0 20 | 5 0 5 5 0 | * 16 * rawvtip
30 | 90 | 20 0 30 20 | 0 10 5 0 5 | * * 16 sirdop
Polyhedron Dude wrote:... Raccoth - retrocelli32-16teron - its facets are 32 firps (purple and green), 16 garpops (yellow), and 40 ohopes (red).
http://pages.suddenlink.net/hedrondude/raccoth.png
12 | 2 2 2 2 | 1 3 3 6 2 2 | 1 1 3 5
---+-------------+----------------+---------
2 | 12 * * * | 1 1 1 0 1 0 | 1 1 0 2 ab x
2 | * 12 * * | 0 2 0 2 0 0 | 1 0 1 2 ae q
2 | * * 12 * | 0 0 2 2 0 1 | 0 1 2 2 ah q
2 | * * * 12 | 0 0 0 2 1 1 | 0 0 2 2 ak h
---+-------------+----------------+---------
3 | 3 0 0 0 | 4 * * * * * | 1 1 0 0 abc xxx = verf(tet)
3 | 1 2 0 0 | * 12 * * * * | 1 0 0 1 abf xqq = verf(trip)
3 | 1 0 2 0 | * * 12 * * * | 0 1 0 1 abi xqq = verf(trip)
3 | 0 1 1 1 | * * * 24 * * | 0 0 1 1 aeh qqh = verf(hip)
4 | 2 0 0 2 | * * * * 6 * | 0 0 0 2 abjkxh(-x)h = verf(oho)
4 | 0 0 2 2 | * * * * * 6 | 0 0 2 0 adhk qh(-q)h = verf(cho)
---+-------------+----------------+---------
6 | 6 6 0 0 | 2 6 0 0 0 0 | 2 * * * abcdef verf(firp)
6 | 6 0 6 0 | 2 0 6 0 0 0 | * 2 * * abcghi verf(firp)
6 | 0 2 4 4 | 0 0 0 4 0 2 | * * 6 * abdeil verf(garpop)
5 | 2 2 2 2 | 2 1 1 2 1 0 | * * * 12 abfjk verf(ohope)
80 | 12 | 12 12 12 12 | 4 12 12 24 6 6 | 2 2 6 12
---+-----+-----------------+----------------------+------------
2 | 480 | 2 2 2 2 | 1 3 3 6 2 2 | 1 1 3 5
---+-----+-----------------+----------------------+------------
3 | 3 | 320 * * * | 1 1 1 0 1 0 | 1 1 0 2
4 | 4 | * 240 * * | 0 2 0 2 0 0 | 1 0 1 2
4 | 4 | * * 240 * | 0 0 2 2 0 1 | 0 1 2 2
6 | 6 | * * * 160 | 0 0 0 2 1 1 | 0 0 2 2
---+-----+-----------------+----------------------+------------
4 | 6 | 4 0 0 0 | 80 * * * * * | 1 1 0 0 tet
6 | 9 | 2 3 0 0 | * 160 * * * * | 1 0 0 1 trip
6 | 9 | 2 0 3 0 | * * 160 * * * | 0 1 0 1 trip
12 | 18 | 0 3 3 2 | * * * 160 * * | 0 0 1 1 hip
12 | 24 | 8 0 0 4 | * * * * 40 * | 0 0 0 2 oho
12 | 24 | 0 0 6 4 | * * * * * 40 | 0 0 2 0 cho
---+-----+-----------------+----------------------+------------
10 | 30 | 20 15 0 0 | 5 10 0 0 0 0 | 16 * * * firp
10 | 30 | 20 0 15 0 | 5 0 10 0 0 0 | * 16 * * firp
30 | 90 | 0 15 30 20 | 0 0 0 10 0 5 | * * 16 * garpop
24 | 60 | 16 12 12 8 | 0 4 4 4 2 0 | * * * 40 ohope
Klitzing wrote:...Polyhedron Dude wrote:... Today's polyteron is Gancpan and boy does it look "gancsta". This is the great spinocelliprismated penteract. It is one of seven members of the getitdin regiment - o(o'x"x)x = oGx. It is also non-orientable. Its facets are 10 girpdohs (yellow), 10 gnappoths (cyan), 32 tips (red), and 80 tuttips (blue). I just added the girpdo macros to my sectioning program a couple days ago. ...
--- rk
x3x3o3o *b4/3x4*c
. . . . . | 640 | 1 3 3 | 3 3 3 3 3 | 3 3 3 1 3 1 | 1 3 1 1
------------------+-----+-------------+---------------------+----------------------+------------
x . . . . | 2 | 320 * * | 3 3 0 0 0 | 3 3 3 0 0 0 | 1 3 1 0
. x . . . | 2 | * 960 * | 1 0 2 1 0 | 2 1 0 1 2 0 | 1 2 0 1
. . . . x | 2 | * * 960 | 0 1 0 1 2 | 0 1 2 0 2 1 | 0 2 1 1
------------------+-----+-------------+---------------------+----------------------+------------
x3x . . . | 6 | 3 3 0 | 320 * * * * | 2 1 0 0 0 0 | 1 2 0 0
x . . . x | 4 | 2 0 2 | * 480 * * * | 0 1 2 0 0 0 | 0 2 1 0
. x3o . . | 3 | 0 3 0 | * * 640 * * | 1 0 0 1 1 0 | 1 1 0 1
. x . . *b4/3x | 8 | 0 4 4 | * * * 240 * | 0 1 0 0 2 0 | 0 2 0 1
. . o . x4*c | 4 | 0 0 4 | * * * * 480 | 0 0 1 0 1 1 | 0 1 1 1
------------------+-----+-------------+---------------------+----------------------+------------
x3x3o . . | 12 | 6 12 0 | 4 0 4 0 0 | 160 * * * * * | 1 1 0 0 tut
x3x . . *b4/3x | 48 | 24 24 24 | 8 12 0 6 0 | * 40 * * * * | 0 2 0 0 quitco
x . o . x4*c | 8 | 4 0 8 | 0 4 0 0 2 | * * 240 * * * | 0 1 1 0 cube
. x3o3o . | 4 | 0 6 0 | 0 0 4 0 0 | * * * 160 * * | 1 0 0 1 tet
. x3o . *b4/3x4*c | 24 | 0 24 24 | 0 0 8 6 6 | * * * * 80 * | 0 1 0 1 gocco
. . o3o x4*c | 8 | 0 0 12 | 0 0 0 0 6 | * * * * * 80 | 0 0 1 1 cube
------------------+-----+-------------+---------------------+----------------------+------------
x3x3o3o . | 20 | 10 30 0 | 10 0 20 0 0 | 5 0 0 5 0 0 | 32 * * * tip
x3x3o . *b4/3x4*c | 192 | 96 192 192 | 64 96 64 48 48 | 16 8 24 0 8 0 | * 10 * * gichado
x . o3o x4*c | 16 | 8 0 24 | 0 12 0 0 12 | 0 0 6 0 0 2 | * * 40 * tes
. x3o3o *b4/3x4*c | 64 | 0 96 96 | 0 0 64 24 48 | 0 0 0 16 8 8 | * * * 10 gittith
Klitzing wrote:...Polyhedron Dude wrote:This one is Kafandoh - spikifacetospinodishexadecateron. It is one of the 37 members of the sirhin regiment and it's non-orientable. Sirhin's symbol is oxo6. It's facets are 16 garpops (cyan) and 16 ripdips (peach). I've rendered only a quadrant of the sections (like I did with gibtadin), the bottom right section is the center section. This one has an interesting structure to it. Below are the sections and verf. ...
--- rk
x3o3o *b3x3o
. . . . . | 160 | 3 6 | 3 6 6 3 | 1 6 3 2 3 | 2 3 1
-------------+-----+---------+-----------------+----------------+---------
x . . . . | 2 | 240 * | 2 2 0 0 | 1 4 1 0 0 | 2 2 0
. . . x . | 2 | * 480 | 0 1 2 1 | 0 2 1 1 2 | 1 2 1
-------------+-----+---------+-----------------+----------------+---------
x3o . . . | 3 | 3 0 | 160 * * * | 1 2 0 0 0 | 2 1 0
x . . x . | 4 | 2 2 | * 240 * * | 0 2 1 0 0 | 1 2 0
. o . *b3x . | 3 | 0 3 | * * 320 * | 0 1 0 1 1 | 1 1 1
. . . x3o | 3 | 0 3 | * * * 160 | 0 0 1 0 2 | 0 2 1
-------------+-----+---------+-----------------+----------------+---------
x3o3o . . | 4 | 6 0 | 4 0 0 0 | 40 * * * * | 2 0 0 tet
x3o . *b3x . | 12 | 12 12 | 4 6 4 0 | * 80 * * * | 1 1 0 co
x . . x3o | 6 | 3 6 | 0 3 0 2 | * * 80 * * | 0 2 0 trip
. o3o *b3x . | 4 | 0 6 | 0 0 4 0 | * * * 80 * | 1 0 1 tet
. o . *b3x3o | 6 | 0 12 | 0 0 4 4 | * * * * 80 | 0 1 1 oct
-------------+-----+---------+-----------------+----------------+---------
x3o3o *b3x . | 32 | 48 48 | 32 24 32 0 | 8 8 0 8 0 | 10 * * rit
x3o . *b3x3o | 30 | 30 60 | 10 30 20 20 | 0 5 10 0 5 | * 16 * srip
. o3o *b3x3o | 10 | 0 30 | 0 0 20 10 | 0 0 0 5 5 | * * 16 rap
Klitzing wrote:...Polyhedron Dude wrote:Now for an utter nightmare! Gipbin - great prismated biprismatopenteract. It is a member of the fawdint regiment, who's symbol is oGo or o(o'x"x)o. I suspect this one is orientable, so I rendered it as such. Its facets are 10 gittiths (cyan), 32 raps (blue), 40 goccopes (red), 80 opes (yellow), 80 tistodips (orange), and 80 tisdips (green). It also has 10 dippanoth shaped pseudofacets. Only the top-left quadrant of the section field has been rendered - therefore the center of the polytope is the bottom-right section. Now who's up for building a model?...
--- rk
o3x3o3o *b4/3x4*c
. . . . . | 320 | 6 3 | 3 6 6 3 | 3 3 2 6 1 | 1 3 2
------------------+-----+---------+-----------------+------------------+---------
. x . . . | 2 | 960 * | 1 2 1 0 | 2 1 1 2 0 | 1 2 1
. . . . x | 2 | * 480 | 0 0 2 2 | 0 1 0 4 1 | 0 2 2
------------------+-----+---------+-----------------+------------------+---------
o3x . . . | 3 | 3 0 | 320 * * * | 2 1 0 0 0 | 1 2 0
. x3o . . | 3 | 3 0 | * 640 * * | 1 0 1 1 0 | 1 1 1
. x . . *b4/3x | 8 | 4 4 | * * 240 * | 0 1 0 2 0 | 0 2 1
. . o . x4*c | 4 | 0 4 | * * * 240 | 0 0 0 2 1 | 0 1 2
------------------+-----+---------+-----------------+------------------+---------
o3x3o . . | 6 | 12 0 | 4 4 0 0 | 160 * * * * | 1 1 0 oct
o3x . . *b4/3x | 24 | 24 12 | 8 0 6 0 | * 40 * * * | 0 2 0 quith
. x3o3o . | 4 | 6 0 | 0 4 0 0 | * * 160 * * | 1 0 1 tet
. x3o . *b4/3x4*c | 24 | 24 24 | 0 8 6 6 | * * * 80 * | 0 1 1 gocco
. . o3o x4*c | 8 | 0 12 | 0 0 0 6 | * * * * 40 | 0 0 2 cube
------------------+-----+---------+-----------------+------------------+---------
o3x3o3o . | 10 | 30 0 | 10 20 0 0 | 5 0 5 0 0 | 32 * * rap
o3x3o . *b4/3x4*c | 96 | 192 96 | 64 64 48 24 | 16 8 0 8 0 | * 10 * wavitoth
. x3o3o *b4/3x4*c | 64 | 96 96 | 0 64 24 48 | 0 0 16 8 8 | * * 10 gittith
Klitzing wrote:......Polyhedron Dude wrote:This one is up to no good, for it is Bad - biprismatododecateron. It is in the dot regiment, dot being ooxoo. Its facets are 12 firps (cyan and yellow) and 20 triddips (red). Its verf has triddip (triangle duoprism) symmetry. ...
--- rk
o3o3x3o3o
. . . . . | 20 | 9 | 9 9 | 3 9 3 | 3 3 verf=triddip
----------+----+----+-------+----------+----
. . x . . | 2 | 90 | 2 2 | 1 4 1 | 2 2
----------+----+----+-------+----------+----
. o3x . . | 3 | 3 | 60 * | 1 2 0 | 2 1
. . x3o . | 3 | 3 | * 60 | 0 2 1 | 1 2
----------+----+----+-------+----------+----
o3o3x . . | 4 | 6 | 4 0 | 15 * * | 2 0 tet
. o3x3o . | 6 | 12 | 4 4 | * 30 * | 1 1 oct
. . x3o3o | 4 | 6 | 0 4 | * * 15 | 0 2 tet
----------+----+----+-------+----------+----
o3o3x3o . | 10 | 30 | 20 10 | 5 5 0 | 6 * rap
. o3x3o3o | 10 | 30 | 10 20 | 0 5 5 | * 6 rap
or
. . . . . | 20 | 9 | 18 | 6 9 | 6 verf=triddip
-------------+----+----+-----+-------+---
. . x . . | 2 | 90 | 4 | 2 4 | 4
-------------+----+----+-----+-------+---
. o3x . . & | 3 | 3 | 120 | 1 2 | 3
-------------+----+----+-----+-------+---
o3o3x . . & | 4 | 6 | 4 | 30 * | 2 tet
. o3x3o . | 6 | 12 | 8 | * 30 | 2 oct
-------------+----+----+-----+-------+---
o3o3x3o . & | 10 | 30 | 30 | 5 5 | 12 rap
Klitzing wrote:...Polyhedron Dude wrote:Now for a weird looking one - Gloptin = great lapidoprismatotruncated penteract. It belongs to the 7 member quiptin regiment, quiptin's symbol is oxox"x. Gloptin's facets are 10 girpiths (purple), 32 sirdops (cyan), 10 gaqrits (red), and 80 tistodips (yellow). Its verf is a butterfly wedge pyramid. ...
--- rk
o3x3o3x4/3x
. . . . . | 960 | 4 2 1 | 2 2 4 4 1 2 | 1 2 2 2 2 4 1 | 1 1 2 2
------------+-----+--------------+-------------------------+----------------------------+------------
. x . . . | 2 | 1920 * * | 1 1 1 1 0 0 | 1 1 1 1 1 1 0 | 1 1 1 1
. . . x . | 2 | * 960 * | 0 0 2 0 1 1 | 0 1 0 2 0 2 1 | 1 0 1 2
. . . . x | 2 | * * 480 | 0 0 0 4 0 2 | 0 0 2 0 2 4 1 | 0 1 2 2
------------+-----+--------------+-------------------------+----------------------------+------------
o3x . . . | 3 | 3 0 0 | 640 * * * * * | 1 1 1 0 0 0 0 | 1 1 1 0
. x3o . . | 3 | 3 0 0 | * 640 * * * * | 1 0 0 1 1 0 0 | 1 1 0 1
. x . x . | 4 | 2 2 0 | * * 960 * * * | 0 1 0 1 0 1 0 | 1 0 1 1
. x . . x | 4 | 2 0 2 | * * * 960 * * | 0 0 1 0 1 1 0 | 0 1 1 1
. . o3x . | 3 | 0 3 0 | * * * * 320 * | 0 0 0 2 0 0 1 | 1 0 0 2
. . . x4/3x | 8 | 0 4 4 | * * * * * 240 | 0 0 0 0 0 2 1 | 0 0 1 2
------------+-----+--------------+-------------------------+----------------------------+------------
o3x3o . . | 6 | 12 0 0 | 4 4 0 0 0 0 | 160 * * * * * * | 1 1 0 0 oct
o3x . x . | 6 | 6 3 0 | 2 0 3 0 0 0 | * 320 * * * * * | 1 0 1 0 trip
o3x . . x | 6 | 6 0 3 | 2 0 0 3 0 0 | * * 320 * * * * | 0 1 1 0 trip
. x3o3x . | 12 | 12 12 0 | 0 4 6 0 4 0 | * * * 160 * * * | 1 0 0 1 co
. x3o . x | 6 | 6 0 3 | 0 2 0 3 0 0 | * * * * 320 * * | 0 1 0 1 trip
. x . x4/3x | 16 | 8 8 8 | 0 0 4 4 2 2 | * * * * * 240 * | 0 0 1 1 stop
. . o3x4/3x | 24 | 0 24 12 | 0 0 0 0 8 6 | * * * * * * 40 | 0 0 0 2 quith
------------+-----+--------------+-------------------------+----------------------------+------------
o3x3o3x . | 30 | 60 30 0 | 20 20 30 0 10 0 | 5 10 0 5 0 0 0 | 32 * * * srip
o3x3o . x | 12 | 24 0 6 | 8 8 0 12 0 0 | 2 0 4 0 4 0 0 | * 80 * * ope
o3x . x4/3x | 24 | 24 12 12 | 8 0 12 12 0 3 | 0 4 4 0 0 3 0 | * * 80 * tistodip
. x3o3x4/3x | 192 | 192 192 96 | 0 64 96 96 64 48 | 0 0 0 16 32 24 8 | * * * 10 quiproh






Polyhedron Dude wrote:Today we have three polytera, all belonging to the scad regiment.
Scad - small cellated dodecateron, also called stericated hexateron - symbol is xooox. The scad regiment has 11 members. Its facets are 12 pens (yellow and magenta), 30 tepes(blue and red), and 20 triddips (green).
http://pages.suddenlink.net/hedrondude/scad.png ...
x3o3o3o3x
. . . . . | 30 | 4 4 | 6 12 6 | 4 12 12 4 | 1 4 6 4 1
----------+----+-------+----------+-------------+-------------
x . . . . | 2 | 60 * | 3 3 0 | 3 6 3 0 | 1 3 3 1 0
. . . . x | 2 | * 60 | 0 3 3 | 0 3 6 3 | 0 1 3 3 1
----------+----+-------+----------+-------------+-------------
x3o . . . | 3 | 3 0 | 60 * * | 2 2 0 0 | 1 2 1 0 0
x . . . x | 4 | 2 2 | * 90 * | 0 2 2 0 | 0 1 2 1 0
. . . o3x | 3 | 0 3 | * * 60 | 0 0 2 2 | 0 0 1 2 1
----------+----+-------+----------+-------------+-------------
x3o3o . . | 4 | 6 0 | 4 0 0 | 30 * * * | 1 1 0 0 0 tet
x3o . . x | 6 | 6 3 | 2 3 0 | * 60 * * | 0 1 1 0 0 trip
x . . o3x | 6 | 3 6 | 0 3 2 | * * 60 * | 0 0 1 1 0 trip
. . o3o3x | 4 | 0 6 | 0 0 4 | * * * 30 | 0 0 0 1 1 tet
----------+----+-------+----------+-------------+-------------
x3o3o3o . | 5 | 10 0 | 10 0 0 | 5 0 0 0 | 6 * * * * pen
x3o3o . x | 8 | 12 4 | 8 6 0 | 2 4 0 0 | * 15 * * * tepe
x3o . o3x | 9 | 9 9 | 3 9 3 | 0 3 3 0 | * * 20 * * triddip
x . o3o3x | 8 | 4 12 | 0 6 8 | 0 0 4 2 | * * * 15 * tepe
. o3o3o3x | 5 | 0 10 | 0 0 10 | 0 0 0 5 | * * * * 6 pen
or, using additional symmetry:
. . . . . | 30 | 8 | 12 12 | 8 24 | 2 8 6
-------------+----+-----+--------+--------+---------
x . . . . & | 2 | 120 | 3 3 | 3 9 | 1 4 3
-------------+----+-----+--------+--------+---------
x3o . . . & | 3 | 3 | 120 * | 2 2 | 1 2 1
x . . . x | 4 | 4 | * 90 | 0 4 | 0 2 2
-------------+----+-----+--------+--------+---------
x3o3o . . & | 4 | 6 | 4 0 | 60 * | 1 1 0 tet
x3o . . x & | 6 | 9 | 2 3 | * 120 | 0 1 1 trip
-------------+----+-----+--------+--------+---------
x3o3o3o . & | 5 | 10 | 10 0 | 5 0 | 12 * * pen
x3o3o . x & | 8 | 16 | 8 6 | 2 4 | * 30 * tepe
x3o . o3x | 9 | 18 | 6 9 | 0 6 | * * 20 triddip
Polyhedron Dude wrote:... Dibhid - dodecabiprismatohemidodecateron. Dibhid is pronounced like DIV vid. Its facets are 12 pens (red and green), 20 triddips (yellow), and 6 spids (blue).
http://pages.suddenlink.net/hedrondude/dibhid.png ...
Vertex Pattern:
b e f
h
a
d c g
8 | 3 3 | 3 9 | 1 3 3
--+-------+------+------
2 | 12 * | 2 2 | 1 2 1 ab x
2 | * 12 | 0 4 | 0 2 2 ae q
--+-------+------+------
3 | 3 0 | 8 * | 1 1 0 abc xxx verf(tet)
3 | 1 2 | * 24 | 0 1 1 abf xqq verf(trip)
--+-------+------+------
4 | 6 0 | 4 0 | 2 * * abcd tet = verf(pen)
6 | 6 6 | 2 6 | * 4 * abcegh xo3ox&#q = verf(spid)
4 | 2 4 | 0 4 | * * 6 abgh xo ox&#q = verf(triddip)
30 | 8 | 12 12 | 8 24 | 2 4 6
---+-----+--------+--------+--------
2 | 120 | 3 3 | 3 9 | 1 3 3
---+-----+--------+--------+--------
3 | 3 | 120 * | 2 2 | 1 2 1
4 | 4 | * 90 | 0 4 | 0 2 2
---+-----+--------+--------+--------
4 | 6 | 4 0 | 60 * | 1 1 0 (tet)
6 | 9 | 2 3 | * 120 | 0 1 1 (trip)
---+-----+--------+--------+--------
5 | 10 | 10 0 | 5 0 | 12 * * (pen)
20 | 60 | 40 30 | 10 20 | * 6 * (spid)
9 | 18 | 6 9 | 0 6 | * * 20 (triddip)
Users browsing this forum: No registered users and 27 guests