Klitzing wrote:Yes, formerly you provided one field of sections every 2 days (more or less), and now you accellerated to 2 per day! - Wow
Maybe 0,1, 2, or when feeling festive 3!
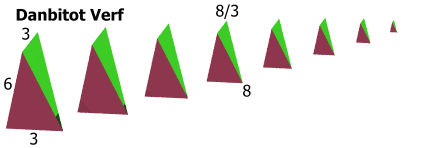
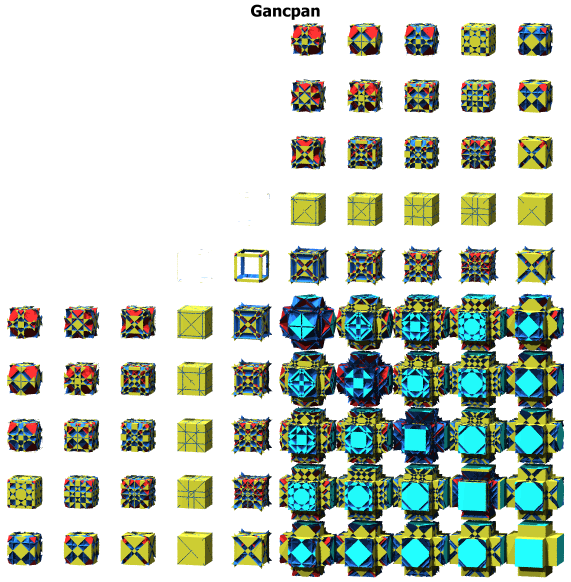
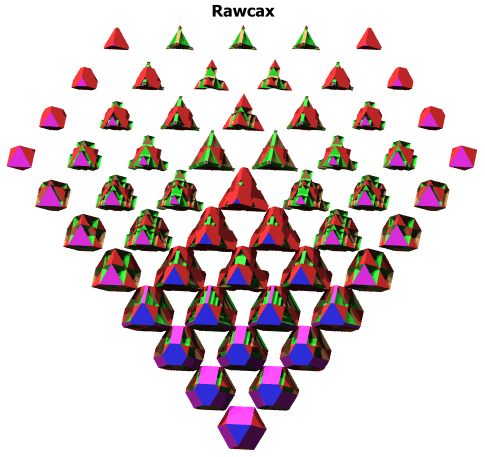
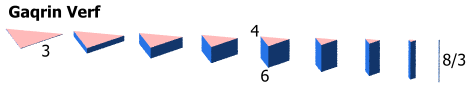
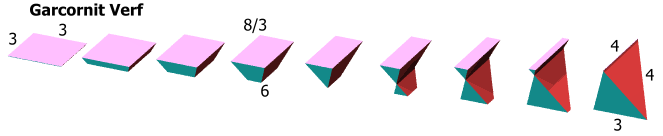
Today there are two. First one is Garcornit - great retrocellirhombated penteracti32. Its symbol is (o'x"(x)o,x) and it belongs to the wacbinant regiment which also contains gadencorn. Its facets are 10 wavitoths (light magenta), 32 rawvtips (blue), 10 giphadoes (cyan), 10 gichadoes (red), and 80 tisdips (wood).
 http://pages.suddenlink.net/hedrondude/garcornit.png
http://pages.suddenlink.net/hedrondude/garcornit.pngThe INC Mat has been provided by Klitzing below.
- Code: Select all
x4/3x4o3*a3o3/2x3*a
. . . . . | 960 | 4 2 2 | 4 2 2 4 1 4 1 | 2 2 4 1 2 2 2 2 | 1 2 2 1 1
--------------------+-----+--------------+-----------------------------+------------------------------+---------------
x . . . . | 2 | 1920 * * | 1 1 1 1 0 0 0 | 1 1 1 1 1 1 0 0 | 1 1 1 1 0
. x . . . | 2 | * 960 * | 2 0 0 0 1 2 0 | 2 1 2 0 0 0 2 1 | 1 2 1 0 1
. . . . x | 2 | * * 960 | 0 0 0 2 0 2 1 | 0 0 2 0 1 2 1 2 | 0 1 2 1 1
--------------------+-----+--------------+-----------------------------+------------------------------+---------------
x4/3x . . . | 8 | 4 4 0 | 480 * * * * * * | 1 1 1 0 0 0 0 0 | 1 1 1 0 0
x . o3*a . . | 3 | 3 0 0 | * 640 * * * * * | 1 0 0 1 1 0 0 0 | 1 1 0 1 0
x . *a3o . | 3 | 3 0 0 | * * 640 * * * * | 0 1 0 1 0 1 0 0 | 1 0 1 1 0
x . . . x3*a | 6 | 3 0 3 | * * * 640 * * * | 0 0 1 0 1 1 0 0 | 0 1 1 1 0
. x4o . . | 4 | 0 4 0 | * * * * 240 * * | 2 0 0 0 0 0 2 0 | 1 2 0 0 1
. x . . x | 4 | 0 2 2 | * * * * * 960 * | 0 0 1 0 0 0 1 1 | 0 1 1 0 1
. . . o3/2x | 3 | 0 0 3 | * * * * * * 320 | 0 0 0 0 0 2 0 2 | 0 0 2 1 1
--------------------+-----+--------------+-----------------------------+------------------------------+---------------
x4/3x4o3*a . . | 24 | 24 24 0 | 6 8 0 0 6 0 0 | 80 * * * * * * * | 1 1 0 0 0 gocco
x4/3x . *a3o . | 24 | 24 12 0 | 6 0 8 0 0 0 0 | * 80 * * * * * * | 1 0 1 0 0 quith
x4/3x . . x3*a | 48 | 24 24 24 | 6 0 0 8 0 12 0 | * * 80 * * * * * | 0 1 1 0 0 quitco
x . o3*a3o . | 6 | 12 0 0 | 0 4 4 0 0 0 0 | * * * 160 * * * * | 1 0 0 1 0 oct
x . o3*a . x3*a | 12 | 12 0 6 | 0 4 0 4 0 0 0 | * * * * 160 * * * | 0 1 0 1 0 tut
x . . *a3o3/2x3*a | 12 | 12 0 12 | 0 0 4 4 0 0 4 | * * * * * 160 * * | 0 0 1 1 0 oho
. x4o . x | 8 | 0 8 4 | 0 0 0 0 2 4 0 | * * * * * * 240 * | 0 1 0 0 1 cube
. x . o3/2x | 6 | 0 3 6 | 0 0 0 0 0 3 2 | * * * * * * * 320 | 0 0 1 0 1 trip
--------------------+-----+--------------+-----------------------------+------------------------------+---------------
x4/3x4o3*a3o . | 96 | 192 96 0 | 48 64 64 0 24 0 0 | 8 8 0 16 0 0 0 0 | 10 * * * * wavitoth
x4/3x4o3*a . x3*a | 192 | 192 192 96 | 48 64 0 64 48 96 0 | 8 0 8 0 16 0 24 0 | * 10 * * * gichado
x4/3x . *a3o3/2x3*a | 192 | 192 96 192 | 48 0 64 64 0 96 64 | 0 8 8 0 0 16 0 32 | * * 10 * * giphado
x . o3*a3o3/2x3*a | 30 | 60 0 30 | 0 20 20 20 0 0 10 | 0 0 0 5 5 5 0 0 | * * * 32 * rawvtip
. x4o o3/2x | 12 | 0 12 12 | 0 0 0 0 3 12 4 | 0 0 0 0 0 0 3 4 | * * * * 80 tisdip
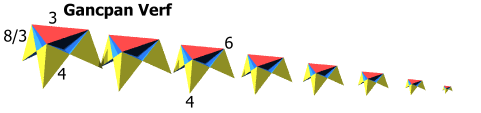
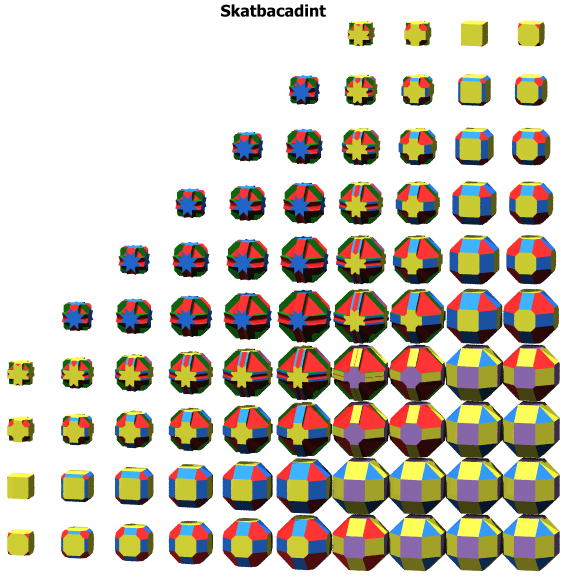
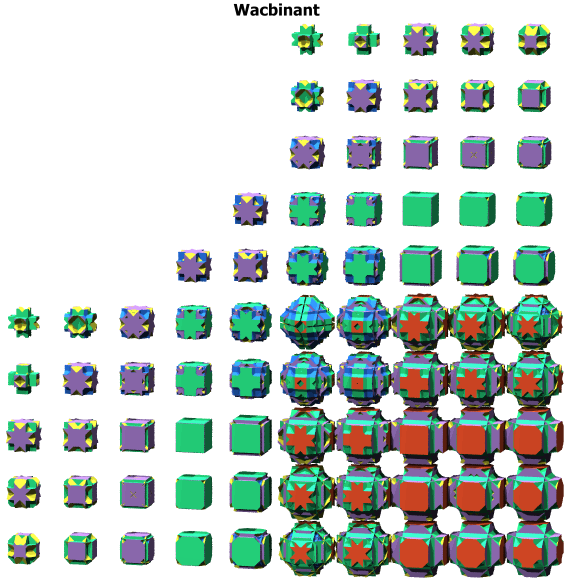
Next polyteron is Wacbinant - sphenary cellibiprismatopenteractipenteracti32. It's symbol is Gox = (o'x"x)ox. Its regiment contains 27 members. Facets are 10 wavitoths (red-orange), 32 srips (yellow), 10 quiprohs (purple), 40 goccopes (aqua), and 80 tisdips (blue).

 http://pages.suddenlink.net/hedrondude/wacbinant.png
http://pages.suddenlink.net/hedrondude/wacbinant.pngWhale Kumtu Dedge Ungol.