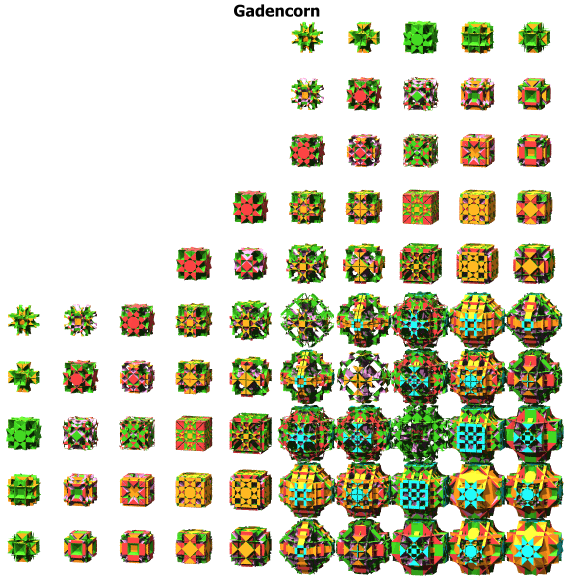
Polyhedron Dude wrote:quickfur wrote:I like spix. It's nice and simple, yet intricate in its own way.

Of course, I'm partial to convex polytopes... but the others are really nice too. I've been busy and haven't been able to work on my projection-based renders recently, but I've still been thinking at the back of my mind about how to deal with rendering projections of non-convex polytopes. Well, in principle I know what needs to be done, but it's just a matter of how to implement it.

I do find the projection method more intuitive (for me, anyway) than sectioning.
I find your renders quite fascinating, they really help bring out the 4-D-ness of the polychora.
Thanks!
Sectioning works well with star polytopes to bring out the intersection details, but you do lose that 4-D effect.
Sectioning does have one advantage over projections: they are not prone to illusions and ambiguity caused by obscuring of elements that overlap in the field of vision. They also let you get "inside" the polytope, esp. a non-convex one, without making it hard or impossible to see where the elements are.
I
am trying to figure out a way of dealing with non-convex polytopes in my renderer, though that's probably not going to happen for a while yet, since I'm currently in the process of rewriting the software for it. The current program I wrote, while it works, has a lot of hacks and limitations, and worst of all, performance problems with large polytopes. My last polytope-of-the-month renders, for example, took excruciatingly long to render, and I'm not even dealing with the most complex 4D polychoron yet. Its smooth-surface handling is also hacky, which means thus far it can only properly deal with a limited number of curvy shapes (duocylinder, and various circle-polygon cartesian products, but anything much beyond that and it starts to produce strange/wrong output). I'd like to fix up this part as well, to make it possible to render, say, your wonderful regular swirlprisms in projection.
All in all, it adds up to a pretty tall order, so I'm not holding my breath for it to be ready anytime soon.

[...]
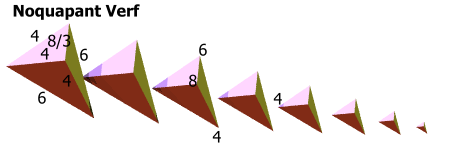
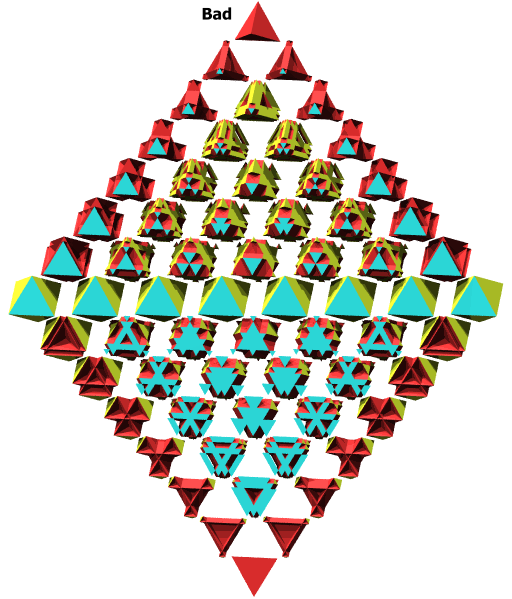
Now for our next polyteron, this one will noqyapants off, its Noquapant. Noquapant is the penteractiquasiprismated penteracti32teron. Its symbol is (x'x"x)xx = Cxx for short. It is a lone operative and is the most amazing looking of the simplex-verfed polytera. Its facets are 10 thaquitpaths (yellow), 10 gaquidpoths (cyan), 32 gippids (green), 80 hodips (red-orange), and 40 cotcopes (lavender).
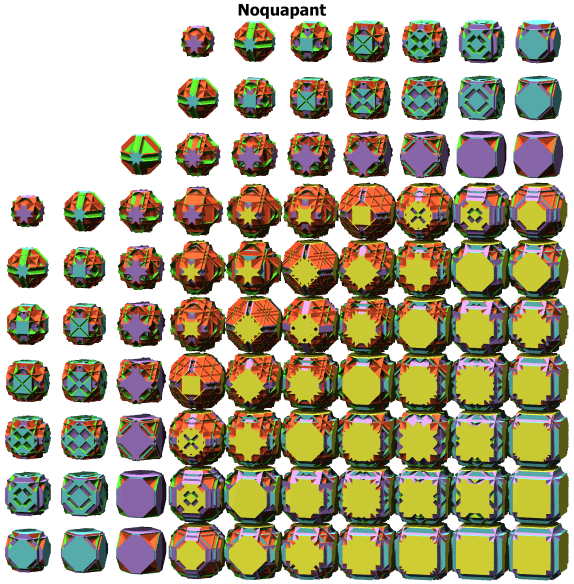 http://pages.suddenlink.net/hedrondude/noquapant.png
http://pages.suddenlink.net/hedrondude/noquapant.png
Whoa. It
is pretty amazing-looking. Some of those sections show incredibly intricate starry patterns where I wouldn't expect it from a 5-cube symmetry! Incredible.
Just out of curiosity, how do you handle coordinates for these polytopes? Do you use full Cartesian coordinates, or just a point and a generating symmetry (via a Wythoff construction perhaps)? Currently, my renderer uses explicit coordinates for vertices, and vertex sets for j-faces. To avoid having to manually specify vertex sets (which is impractical beyond the simplest polychora -- the 24-cell, for example, took me 2 days to write out in full), I use a convex hull algorithm to generate the j-faces. Unfortunately, this means it can't handle non-convex polytopes.
I've been thinking about some kind of automated faceting algorithm for generating non-convex polytopes, though. Is it true that the hyperplanes of all cells in a non-convex uniform polytope always corresponds with (i.e. parallel to)
some element of a
convex uniform polytope? Or are there cases where the hyperplanes are non-parallel to all j-faces of any convex uniform polytope? If the former, I may have an easy way of generating non-convex polytopes; if the latter, then how in general do you construct these things?
(In any case, even if I can generate coordinates for non-convex polytopes, it will still take a while before the renderer can actually handle them correctly, since to produce the correct projection images I'd need full 3D volumetric clipping, and right now I don't have a good way of doing that yet.)

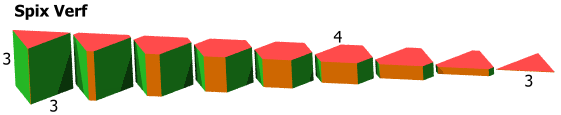
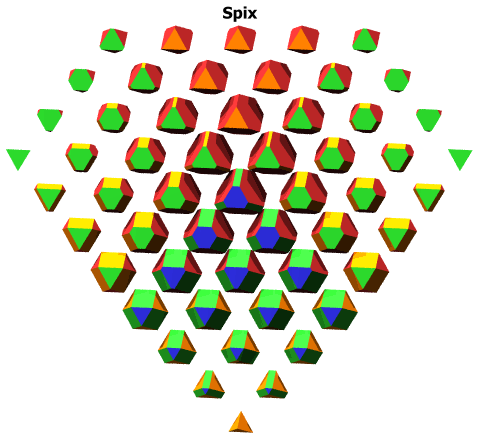 http://pages.suddenlink.net/hedrondude/spix.png
http://pages.suddenlink.net/hedrondude/spix.png


















 Got it!
Got it!