Wireframe spheres [Split from "Quickfur's renders"]

[Secret]

What's a "grided", and what's a hidden surface removed 3-sphere? So far I haven't yet figured out the best way to represent the 3-sphere in a 3D projection, because it is completely smooth and so the current method of rendering ridges only will just produce a 2-sphere, which doesn't help at all in understanding the 3-sphere. The best way I've found is still to examine the various uniform polychora and see how their cells are laid out, because they are all tilings of the 3-sphere.

What I tried to say is this

A wireframe 2 sphere


If applied hidden surface removal, it'll become like this



Can you render a 3 sphere tiled with cubes in a similar fasion as the wireframe thing above, with and without hidden surface removal
-> Sorry but I still find non cubic tiles like those found in the 120 cell and its derivitives confusing

Also can you also render a 3 sphere with a 3D specular point and a 2 sphere with a 2D specular point?

[quickfur]

Ahhh so that's what you meant. OK.

I'm trying to figure out what would be the most obvious subdivision of the 3-sphere's surface. There's the direct analogue, made by great spheres crossing the poles ("longitude spheres") and intersections with horizontal hyperplanes ("latitude spheres"), but the thing is, the longitude great spheres have two degrees of freedom, so it's unclear what's the best way to subdivide the 3-sphere into longitudes.

There's also a more uniform way to subdivide the surface, which is based on the duocylinder (well, the Hopf fibration, really). This one gives two great circles as "poles", with toroidal sheets of varying radii, that subdivide the surface into tori. (Just like what we discussed in the thread on planetary directions.) To these toroidal sheets you'd add a series of great spheres that intersect either of the "great poles" at regular intervals, so as to cut up the tori into cylindrical sections. The result is more uniform, for sure, but will have rather odd-shaped subdivisions.

I guess I might just have to go the direct analogue route, and just randomly pick some subdivision of the longitude spheres. No matter how you pick it, there's gonna be some subdivisions that aren't cubical. There will be some parts that will have to be tetrahedral and/or pyramidal (probably triangular prisms jointed at tetrahedra would be my guess). The problem is that my polytope viewer doesn't really do curved surfaces, so I have to figure out all of this topology before I can generate a polytopic approximation of the 3-sphere based on this kind of subdivision. But I'll try.

[Keiji]

I can imagine the analogue to Secret's second picture quite easily, though I can't really describe it and I'd be hopeless at trying to draw or render it.

I would be more interested though in the duocylinder-style grid. That would be like the 4D planets topic discussed earlier, with independent timezones and climatezones. Trying to imagine this, though, all I ever manage to see is a torus.

[quickfur]

Well then, I definitely should try to do a render of the duocylindrical subdivision of the 3-sphere. For visualization, just imagine the duocylinder where the radius of the two tori are different. Now imagine a whole series of them, starting with the first radius 0 (which gives you one of the circular poles) increasing and the second radius at max decreasing. What you get is, in projection, a series of concentric tori that start out as a single line, expands into a torus, then gets wider, and eventually converges into the complementary circle. This divides the surface of the 3-sphere into toroidal zones, that are essentially torus extrusions of varying major/minor radii.

The keyword is concentric.

[Keiji]

I can see the concentric torii expanding, but I can't picture how it gets from there to the perpendicular circle.

[quickfur]

I can see the concentric torii expanding, but I can't picture how it gets from there to the perpendicular circle.

Just think of the duocylinder; each of its bounding tori has a radius, and they can actually be varied continuously. So start with the first radius 0 (which collapses the duocylinder into a circle), then increase it while decreasing the second radius, until it becomes 0.

[Marek14]

I was thinking about the subdivision of 3-sphere recently.

The way I visualise the 3-sphere is as a solid ball where the border of the ball is "equator" and everything inside forms one half of the 3-sphere. The other half would be actually mapped on the whole rest of 3-space, which can help when visualising the constant coordinates surfaces.

First division is the extension of normal 2-sphere coordinates, based on parametric equations:

x = r cos a cos b cos c
y = r cos a cos b sin c
z = r cos a sin b
w = r sin a

This leads to three kinds of surfaces:

I. a = const.

This surface is a 2-sphere in xyz-oriented hyperplane with a constant w coordinate. In the projection, a=0 sphere would be equator, and the others would be concentric. At the extreme (a = +- pi/2), you'd get two poles, one in the center of projection and the other in infinity.

II. b = const.

For b = 0, this is a 2-sphere in xyw hyperplane. For b = pi/2, this is a circle in zw plane. Points [0,0,0,r] and [0,0,0,-r] lie on all b-constant surfaces. Not sure how the in-between surfaces look in 4D, but in 3D projection, I think they would be cones connecting constant latitude-lines on the surface of the projection sphere with its center. For b = 0, this is the equator plane, for b = pi/2 it's just a single line joining the center with the North Pole.

III. c = const.

Since only x and y use the c parameter, all constant-c surfaces contain the circle in zw plane. All of these surfaces are sphere which lie in zwu hyperplane, where "u" is some direction in xy plane. In the projection, these are meridians on the projection sphere, together with all points below the surface up to the axis.

Second division is the duocylindrical one:

x = r cos a cos b
y = r cos a sin b
z = r sin a cos c
w = r sin a sin c

I. a = const.

For a = 0 this is a circle in xy plane (equator of projection sphere), while for a = pi/2 it's a circle in zw plane (axis of projection sphere). The shapes in-between are duocylinders, and in projection the do indeed look like toruses. How does the transition look? Here we can use the fact that the second half of the 3-sphere is mapped to the whole space outside the projection sphere. As a grows, the outer radius of the toruses grows indefinitely, and so does the inner radius. For high a, you're looking at a huge, fat torus with a comparatively tiny hole - so tiny that the hole starts looking more and more like a tube of constant width. This is why we'll get the axis of the projection sphere in the limit.

II. b = const.

These are spheres in zwu hyperplanes where "u" is a direction in xy plane. It's the exact same definition as constant-c surfaces in first subdivision, and therefore it projects in the same way.

III. c = const.

These are spheres in xyu hyperplanes where "u" is a direction in zw plane. In projection, all of them pass through the equator of projection sphere. For c = 0 we get the projection sphere, and for c = pi/2 we get the equatorial plane. For other values, we get various spheres that are centered on the axis and pass through the equator.

[quickfur]

[...]
The way I visualise the 3-sphere is as a solid ball where the border of the ball is "equator" and everything inside forms one half of the 3-sphere. The other half would be actually mapped on the whole rest of 3-space, which can help when visualising the constant coordinates surfaces.

Or you could visualize it as two such solid balls whose spherical surfaces are attached to each other (but the two interiors are distinct). Each ball would be half of the 3-sphere's surface, and the spherical boundary would be the equator.

As for the rest of your equations, thanks, i'll take a look at them sometime to see if I can generate a polytopic approximation using them, that I can feed to my renderer.

[Marek14]

Yes, but I specifically map the other half on the rest of the space since this helps visualising some of the surfaces (a and c surfaces of the duocylindrical subdivision). Under your projection, they would be harder for imagine for some people.

[quickfur]

Alright folks, here's my first stab at rendering the 3-sphere using a squarish grid:



This is the most direct analogue of the picture that Secret posted. It's basically stacking a bunch of those 2-sphere grids together in 4D, scaled so that they gird the 3-sphere. In the above projection, you can see these 2-sphere grids stacked vertically, with cells formed by extrusion between layers (which also involves some scaling). Some hexahedral cells did come up, which is good, but there is an entire great circle running from north to south where these cells converge into triangular wedges. If you look carefully, you can see that the upper layers are slightly concave downwards (bulging upwards); this is analogous to a perspective projection of the 2-sphere grid when you look straight at the equator; the northern latitude lines curve upwards slightly. Conversely, the lower layers are concave upwards (they curve downwards), due to the same effect.

In terms of actual equations, it so happened that this is actually the most straightforward parametrization of the 3-sphere:

w = r cos A
x = r sin A cos B
y = r sin A sin B cos C
z = r sin A sin C sin C

where A, B, and C are sampled at regular intervals. This particular render was done by doing 16 samples per angle. There are 800 vertices in total, and 1024 cells. Obviously I'm using HSR so only the cells lying on the near side are visible here.

[Keiji]

Hmm... I'm surprised that there aren't square based pyramids all pointing to the centre with cubes radiating out from there in concentric spheres.

Perhaps this is a different projection? Or is there another parameterization?

[quickfur]

And for comparison, here's an analogous projection of the 2-sphere with the analogous set of parameters:



Note that the analogy is not perfect, since in the case of the 3-sphere we applied another layer of gridding to each latitude, whereas here we just use a regular polygon in each layer. But you should be able to see some analogies between these two projections.

[Keiji]

Oh, that answered my question... the "apex" isn't visible in that projection of the 2-sphere.

Could you please render another projection with the 3-sphere rotated around so that the "apex" is visible, say, 1/4 way down?

[quickfur]

Hmm... I'm surprised that there aren't square based pyramids all pointing to the centre with cubes radiating out from there in concentric spheres.

Perhaps this is a different projection? Or is there another parameterization?

There are many parametrizations... this one is the simplest, but unfortunately also the ugliest. :/

The problem is that the 2-sphere cannot be tiled evenly by tetragons, so you're bound to have some kind of point of convergence, which turns into a line of convergence when you extend it to the 3-sphere. I could shift the viewpoint so that a cubical column projects to the center of the image, but you will still see the convergence line somewhere. The duocylindrical grid, however, does not suffer from this due to the Hopf fibration. But then it also introduces toroidal elements which some people may find equally confusing.

[Keiji]

See this post:

Oh, that answered my question... the "apex" isn't visible in that projection of the 2-sphere.

Could you please render another projection with the 3-sphere rotated around so that the "apex" is visible, say, 1/4 way down?

I wanted to see the convergence point.

[Marek14]

Hmm... I'm surprised that there aren't square based pyramids all pointing to the centre with cubes radiating out from there in concentric spheres.

Perhaps this is a different projection? Or is there another parameterization?

There are many parametrizations... this one is the simplest, but unfortunately also the ugliest. :/

The problem is that the 2-sphere cannot be tiled evenly by tetragons, so you're bound to have some kind of point of convergence, which turns into a line of convergence when you extend it to the 3-sphere. I could shift the viewpoint so that a cubical column projects to the center of the image, but you will still see the convergence line somewhere. The duocylindrical grid, however, does not suffer from this due to the Hopf fibration. But then it also introduces toroidal elements which some people may find equally confusing.

Basically, there is a theorem which states that you can't assign every point of 2-sphere a direction in such a way that the directions would vary continuously (or, more colloquially, "you can't comb a hairy ball so it's smooth"). On Earth, no compass direction is universal (having a definite direction at each point).

Torus, on the other hand, can be smoothed in this way, you can have directions corresponding to major circles, minor circles or various spirals, and they will all have perfectly good meaning at each point - one of the reasons why torus geometry is so popular in videogames!

Not sure how it works on 4-sphere. With the duocylindrical parametrization, most of "layers" is between two toroidal-geometry surfaces, and so they can be cut into neat cuboids, but near the two polar circles, the tiles would be still squashed into triangular prisms and no cardinal direction seems to be truly universal (the main direction "ends" on polar circles while the other ones (b and c in parametrization) are defined everywhere except for one or the other polar circle). Maybe an universal direction could be one that would, in a definable way, "morph" between b direction at one polar circle and c direction at the other?

[wendy]

You can easily prove that for any even dimension, it is possible to comb a ball, by this trick.

A sphere of 2N dimensions, can be represented as a set of N complex dimensions, (ie CEn), for which one can take any point, and multiply its coordinates x1..xn, by some w(t) [omega*time, where omega is a unit complex number]. Since this does a single trace around the centre for every point, then the sphere in N dimensions is indeed can be completely combed.

You might note in 4d, this is the clifford-parallels,

Also, in four dimensions, suppose you write w,x, y,z as w+ix, y+iz. Then, any two points in this space, will define a 2-space, which is a clifford-parallel to the base set, and therefore clifford-parallel (ie maintain a constant angle, and have a preset arrow around it). For any given point, the second point is (0,0). The direction can be determined by multiplying by 'i' throughout, ie w+ix, y+iz becomes -x+iw, -z+iy.

[quickfur]

See this post:

Oh, that answered my question... the "apex" isn't visible in that projection of the 2-sphere.

Could you please render another projection with the 3-sphere rotated around so that the "apex" is visible, say, 1/4 way down?

I wanted to see the convergence point.

There is no single convergence point; there is a convergence line all around a great circle. That's the line through the center of the projection that you see above. Like I said, the analogy with the 3D case is not perfect. In 3D, due to the "hairy ball" theorem, there will always be two poles where there is divergence or convergence. In this particular subdivision of the 3-sphere, we are stacking these "hairy balls" along the W axis, so their convergence points line up along a single great circle. That great circle is where everything converges; it is not confined to a single point.

I'm now working on another subdivision of the 3-sphere, which may be more helpful in visualizing its curvature: basically it's the intersection of the 3-sphere with hyperplanes parallel to the coordinate axes. The 3D equivalent of this may be thought of as the rubik's cube subdivision of the 2-sphere. The 2-sphere will have 8 corners, corresponding with the cube's vertices, where these intersection lines would converge; the 3-sphere likewise will have 16 corners where these lines converge - at these convergence points there will be tetrahedral cells; emanating from them will be lines of triangular prisms (corresponding with the edges of the 4-cube). The rest of the surface would have (more or less) cubical subdivisions.

[quickfur]

[...]
There is no single convergence point; there is a convergence line all around a great circle.
[...]

Actually, scratch that. That's wrong. There is a point of convergence because I'm basically doing horizontal slices across the 3-sphere, and applying the grid pattern to each of the spherical slices that I make (the slices are not the same radius; slices near the poles are smaller at the slice at the pole is a point, so the cells surrounding that would be pyramids).

Anyway. Nothing like a real projection from my renderer to prove that I was wrong:



Isn't that pretty? Here, I've shifted the viewpoint to look directly at a pole. That it is a convergence point is indisputably clear. The conical slices are actually spindles; they wrap around the 3quator (the boundary of this projection) and converge onto the opposite pole. The horizontal disk in the middle is actually a sphere; the rest of the conical slices are narrower spindles. The concentric spheres you see here show the cross-sections that the 3-sphere makes with parallel hyperplanes.

[quickfur]

P.S. Actually I like this viewpoint much better that the one I had before. Here you can see several other features of interest:

• If you look carefully, you can see vertical circular sections that rotate around the vertical axis of the projection. These are actually spheres. So this particular subdivision of the 3-sphere can also be constructed by rotating a 2-sphere in the xyz plane around the wx plane (or an equivalent such combination).
• The apparent vertical line around which these circular sections rotate is the same great circle that everything converges at, in the previous projection. This is the vertical line down the center of this projection.
• You can see, by the spacing of the concentric spheres, which is widest in the innermost sphere and closest in the outermost spheres, that around the center region the curvature of the 3-sphere is very close to a flat hyperplane, but as you approach the edges, it starts to "squish" together, that is, it starts to curve away in the 4th direction. So this is actually a not-bad depiction of the curvature of the 3-sphere after all.
• You can also see that the reduction in apparent distance between concentric spheres doesn't decrease linearly; so the curvature is not like a spherical cone, but is a spherical reduction (d = sqrt(x^2+y^2+...)).
• You can actually see pyramidal spikes converging on the center. These pyramidal spikes are actually spindles with a square cross section; they invert on the far side of the 3-sphere and converge into a second apex at the antipodal pole. Each of these things corresponds with the spindle-shaped area on a 2-sphere between two adjacent longitude lines. (Think of what a "gridded" 2-sphere looks like when viewed from the north/south pole: the area between two longitudinal lines appears as a triangular region converging on the pole.)

[quickfur]

You can easily prove that for any even dimension, it is possible to comb a ball, by this trick.
[...]

The way I see it, is that in even dimensions (say 2N dimensions), you have the analogue of the duocylinder: the Cartesian products of N circles. By varying the N radii of the circles while making sure that the resulting points all lie on the 2N-sphere, you obtain a toroidal subdivision of the 2N-sphere's surface, which then lets you "comb" the 2N-sphere without any convergence/divergence points.

[quickfur]

Alright, I now have the 4D analogue to Secret's image:



Here:



Again, the analogy is not perfect, because of the different topological nature of the 3-sphere, but you do see the analogous parts of it. The point where all the pyramids converge to are analogous to the pole where the meridians meet in the 3D case. The spherical shells are the analogues of the latitude lines in the 3D case.

The huge number of edges does make the image quite messy, but at least it shows all these different analogues in a single image. To be honest, I can't say for sure which of the concave spherical shell fragments are the equator, but then, neither can you easily tell in the 3D case. Regardless, you can definitely see the spherical nature of the equator here. (Or rather, the half of the equator visible on the near side; the "top half" lies on the far side of the 3-sphere.)

Unlike the 3D case, where all the meridians are equivalent, the 4D case here has a particular great circle (projected as the line down the middle of this image) where the edges of each of the spherical shells converge, so it is distinguished from the other great circles. This is an artifact of this particular subdivision of the 3-sphere's surface; the 3-sphere on its own, of course, has no such distinguished great circle.

In this projection, also, you see that the conical sections in the previous projection are not really straight cones; they are spindles (here only half of the spindle is visible, as the other half lies on the far side).

[Secret]

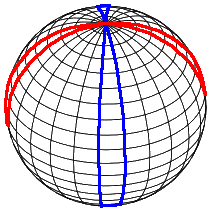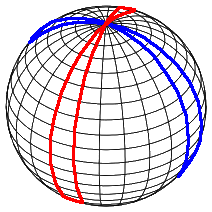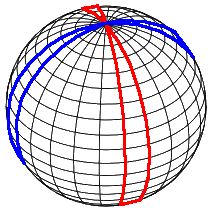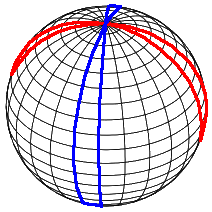
3 Sphere curvature highlighted
Note that the analogy fails for the green bit



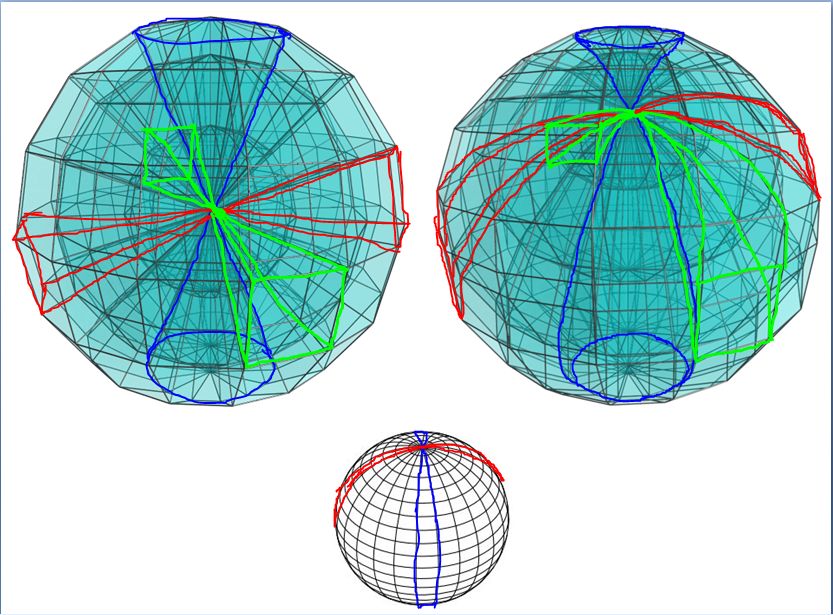
From here, it can be seen that the spindles are 3D objects that lines the rind of the 3 sphere, analogous to how the spindles lines the surface of the 2 sphere

In my perspective:
It seems the moment you tried to highlight the spindles, the spheres become flattened and sew together and become progressively bent towards south as it approaches the boundary sphere/biggest sphere in the projection (the spherical 3quator)

However the green part is still beyond comprehension, other than the fact that I know it is bent, but cannot seemed to fit the view nicely with a bent spherical cloth

####
When switching interpretation A, the thing become hollow and saw the surface become 'paper thin' and the 3D bits bent like pieces of paper and apparently lose their 3D-ness. When switching to another interpretation, the whole thing is puffed up and 3D but then the hollowness feel dissapears and the 3D bits doesn't looked bent
i.e. I still cannot see the two interpretations at the same time


Diagram of interpretation A:

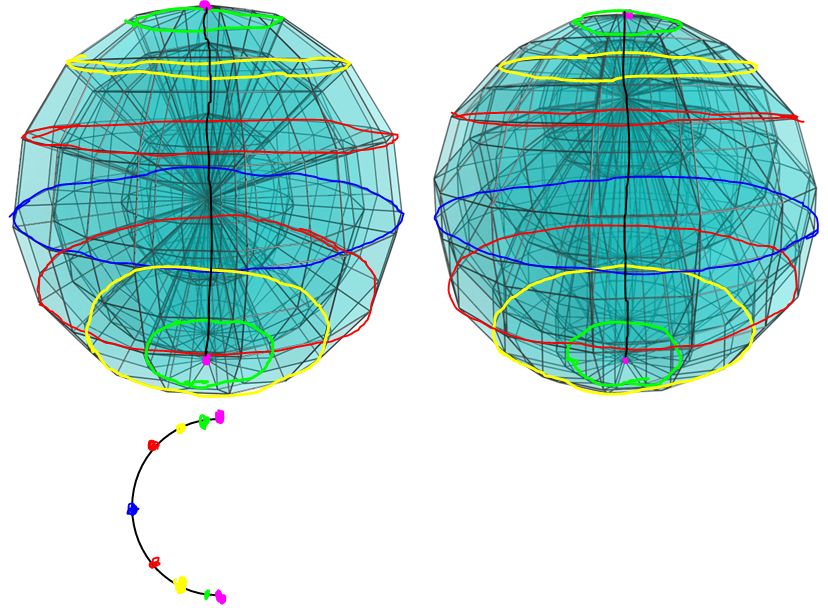
By focusing on the blue circle and with the understanding that the vertical black line is actually something shown the the mini diagram (A semicircle), the whole spherical envelope and volume (in the projection) becomes a huge tubular spindle thing extending from the lower vertex through the north pole to the upper vertex and that the whole thing curve southwards with the smallest sphere in the projection almost 'flat' and the rest of the spheres forming a dome and bend towards the south. The projection now looks like a hemi3 sphere and hollowness is now visible (sort of...)
IMO I think it is easier to see the thing concave northwards rather than convex southwards (do to the 3D shading of the projection)

And this is what I see in intepretation A


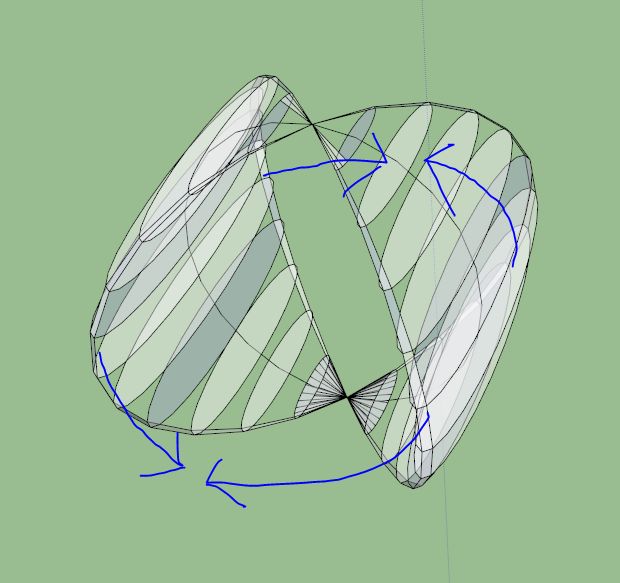
The two spherical spindle halves, folding them together according to the arrows will form a hollow 3 sphere

(However I don't think this is correct cause if this is really the case, then it will be a case where nD stuff embedded in n-1 D space, but not projection)

[quickfur]

3 Sphere curvature highlighted
Note that the analogy fails for the green bit [...]

Actually, the green bits are completely analogous to the red bits. If you rotate the 3D viewpoint a little, you'll see that they're exactly the same.

Of course, they are somewhat different in the sense that there is no 3D analogue to highlighting both the green and red strips simultaneously, because in 3D the sphere only has a 2D area doesn't have that extra degree of freedom, that extra surface area, to fit in both strips at the same time. So whereas the strips emanating from the convergence point in the 2-sphere only wrap around the convergence point in a circle, the analogous strips on the 3-sphere surround the convergence point in a sphere. So that's where the extra dimension fits in.

I'll reply to the rest later... gotta run for now.

[Keiji]

3 Sphere curvature highlighted
Note that the analogy fails for the green bit [...]

Actually, the green bits are completely analogous to the red bits.

And they're both analogous to the blue bits and vice versa. After all, rotating the 2D diagram in 3D will exchange red and blue.

Edit: Here's an animation showing how the red and blue bits are analogous to each other:



This was done manually in the GIMP; it'd be nice if you could get your renderer to output such animations rotating the 3-sphere in the three possible axes (while keeping the actual edges in constant locations, as above), to show how each pair (red/blue, red/green, blue/green) are analogous to each other.

[quickfur]

Hmm, I'll try, but right now the cell selection language is quite low-level, so I have to manually find those cells. It's not as bad as blindly trying all the cells one by one, but it does require some amount of manual typing to find the cells.

Or maybe now's a good time to expand the scripting language to handle looping constructs and variables.

[Keiji]

From here, it can be seen that the spindles are 3D objects that lines the rind of the 3 sphere, analogous to how the spindles lines the surface of the 2 sphere

I like this "rind" term for referring to a 3D boundary of a 4D shape! I've decided to adopt it and added it to the wiki on the Hypercell page.

[quickfur]

From here, it can be seen that the spindles are 3D objects that lines the rind of the 3 sphere, analogous to how the spindles lines the surface of the 2 sphere

I like this "rind" term for referring to a 3D boundary of a 4D shape! I've decided to adopt it and added it to the wiki on the Hypercell page.

I thought Wendy already has a term for it: surchoron.

[quickfur]

Or rather, glomochorix, if you want to be precise (curved 3-manifold).

[Keiji]

We were using "surcell" so far. It doesn't hurt to have some synonyms, though