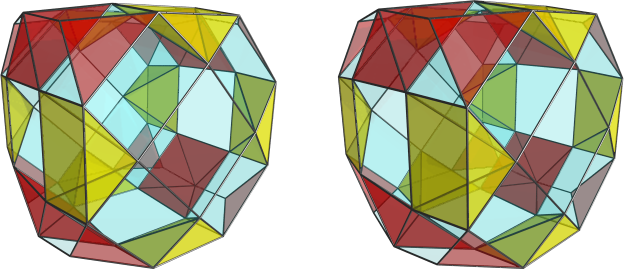
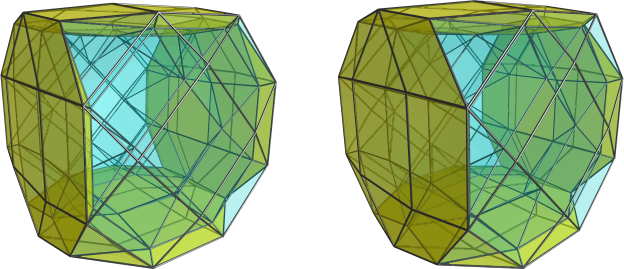
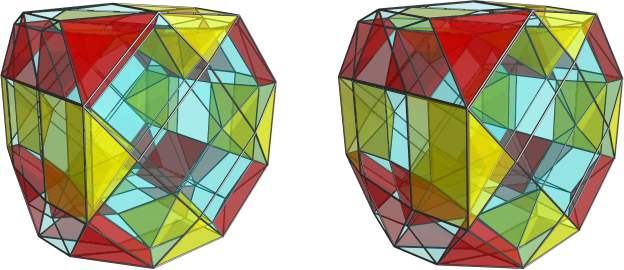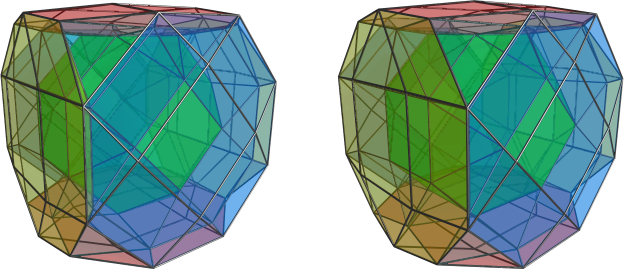Klitzing wrote:[...]
Oh, now I see, were you derive from. You're trying to use para- and meta- in the way Johnson did in naming his solids. But note that there para- does not divide the count! From srid (x3o5x) he derives the para-bi-diminished and the meta-bi-diminished one (resp. -gyrated ones). So you might rather specify your ones as para-8- resp. cyclo-4-.
Well, actually I derived my prefixes by studying the enumeration of all 24-cell diminishings. Maybe using the para-, ortho-, meta- prefixes wasn't a good idea after all; but I wanted some kind of nomenclature that is easy to remember. So I use ortho- for the diminishings that have lots of vertices at 90° from each other, and meta- for the cases where some vertices are ortho to another vertex's antipode, and para for when there are many antipodal points.
Clearly, there is a lot of overlap, and a few ambiguous cases, so I devised a system of numerical prefixes to indicate exactly which vertices are meant. The basic idea was that in any diminishing except the null diminishing (which is uninteresting), there must be at least one vertex, so the numbering of everything else will be relative to this vertex. The second vertex then can only be in 3 distinct positions relative to this vertex, so this stratifies the 24-cell into these cross sections: point -- cube -- octahedron (scaled up by 2) -- cube -- point. By convention, the first vertex is always assigned to the first point, which means that the first cube cannot have any vertices (they are all adjacent to the first point).
Using this stratification, any vertex that lies on the middle octahedron cross-section will be ortho to the first vertex, and any vertex on the second cube will be meta, and the vertex on the last point is para (antipodal). Then to reduce the number of duplicate configurations, I adopt the convention that the canonical prefix is the one that gives the smallest numbers (similar to IUPAC naming for chemical compounds), where the octahedral and cube cross sections are numbered like so:
- Code: Select all
1
| 3'
|/
2---+---2'
/|
3 |
1'
1-----2
/| /|
3-----4 |
| 5---|-6
|/ |/
7-----8
Where 1', 2', 3', are considered to be greater than 1, 2, 3 (I didn't use 4, 5, 6 because I wanted to be able to quickly tell which axis of the octahedron the vertex lies on -- but this scheme can be renamed if it yields a better notation).
The notation then, is made by writing the prefix in the form 1,(1,2,3),(1,2,3),1, where the first number corresponds with the first vertex, the first parentheses list the vertices that lie on the octahedral cross section, the second parentheses list the vertices on the second cube, and the last number is for the antipode (omitted if the antipode is not included in the set). Parentheses are omitted if there's only one vertex from the corresponding cross section. If either of the middle two parentheses are empty, then they are written as 0 instead.
Using this naming system, I enumerated all 24-cell diminishings:
- Code: Select all
- 1-diminished 24-cell ((mono)diminished)
- 1,1-bidiminished 24-cell (orthobidiminished)
- 1,0,1-bidiminished 24-cell (metabidiminished)
- 1,0,0,1-bidiminished 24-cell (parabidiminished)
- 1,(1,2)-tridiminished 24-cell (orthotridiminished)
- 1,(1,1')-tridiminished 24-cell (paratridiminished)
- 1,1,5-tridiminished 24-cell (metatridiminished)
- 1,(1,2,3)-tetradiminished 24-cell (orthotetradiminished)
- 1,(1,2,1')-tetradiminished 24-cell (paratetradiminished)
- 1,(1,2),6-tetradiminished 24-cell (orthometatetradiminished)
- 1,(1,1'),0,1-tetradiminished 24-cell (cyclotetradiminished)
- 1,1,(5,8)-tetradiminished 24-cell (metametatetradiminished)
- 1,(1,2,3,1')-pentadiminished 24-cell (orthopentadiminished)
- 1,(1,2,3),6-pentadiminished 24-cell (metapentadiminished)
- 1,(1,2,1',2')-pentadiminished 24-cell (parapentadiminished)
- 1,(1,2,3,1',2')-hexadiminished 24-cell (orthohexadiminished)
- 1,(1,2,1',2'),0,1-hexadiminished 24-cell (parahexadiminished)
- Heptadiminished 24-cell (augmented tesseract)
- Octadiminished 24-cell (tesseract)
It's arguable whether the names in the parentheses are the best; if you have a better idea, I'd love to hear it. In any case, the simplest improvement of this notation is to elide the first 1, because it's always 1. After that, there may be a way of simplifying the notation to cover all the cases without needing to spell out all the numbers. But the current system is unambiguous, so that's what I've been using up till now.
So far as to the positions of actions. Now to what you are gyrating. You multiply mention some 8-prism||square. So far can't visualize those in srit. Would you come in?
In the mentioned 8 positions there are sirco||tic for cupolae. But those would intersect, if applied at 90° positions. Don't believe that this works in gyration, this most probably would produce some non-CRF cell sections. Isn't it?
Hmm. Did I mix up which polychoron I was applying the gyration to? I was referring to x4o3x3o (or o3x3o4x in your usual way of writing it). It can be decomposed as an 8,8-duoprism augmented with eight 8prism||square's, with 4 in each ring of 8 prisms, each pair separated by an 8-prism. Eight of the 8prisms from the 8,8-duoprism merge with the square cupolas in the augment to form 8 rhombicuboctahedra, and the square pyramids of the augments merge into 16 octahedra.
The result has higher symmetry than the 8,8-duoprism, because of the coincidence of 4pyr + 4pyr = oct, and there are 3 ways to do this, and also 4cup + 8prism + 4cup = rhombicuboctahedron, which has higher symmetry than 4cup and 8prism. So from the x4o3x3o, we are allowed to cut off two 8prism||square as long as the cutting does not cut the same octahedron from two different planes (it will result in a non-CRF). It's OK to cut the same octahedron from both sides if the cutting plane is the same; in this case the entire octahedron is removed from the result, otherwise a square pyramid remains.
Interestingly, not only you can cut off the 8prism||square, but you can also glue it back with the square rotated 45°. The result is that the 4pyrs don't line up, so they don't form octahedra, but remain as 4pyrs. This is what I mean by gyrating. I've posted about the paratetragyrate before, in
this post. It has this image:

If you look at the center part, where the yellow cell and the green cell meet, you can see their common square face, and if you trace the edges outwards by 1 edge length, you can see the outline of an 8-prism. (The triangular prisms + 4pyr are not coplanar so they are not augmented 3prisms or gyrobifastigiums.) This 8-prism is the base of an 8prism||square. If you cut it off, you will get an 8-prism cell here connecting the top part of the yellow cell to the bottom part of the green cell (they will be shortened into elongated square cupola). If you then follow in the same direction along the great circle from the top of the yellow cell to the bottom of the green cell, you can find more 8prism||square augments; you can cut them all off and you will end up with a ring of eight 8prisms.
) Is the bi-24-dim-xoo5x chiral too?








 (@hedrondude)
(@hedrondude)