Marek14 wrote:quickfur wrote:But how would you ensure that the polygons in the net will form convex cells? And how would you guarantee they lie on a single hyperplane? You might get some polygon nets that are non-planar, then you can't make a valid CRF from it.
When adding any single polygon, you could make sure it's planar. As for whether they will form convex cells... if you won't allow coplanar polygons, won't they form convex cells automatically?
What I meant was, how do we know the polygons that surround a cell will lie on a single hyperplane? Each polygon may be planar in itself, but I'm not sure how we can guarantee that putting a bunch of planar polygons together will guarantee cell convexity. From a programmatic point of view, the program wouldn't immediately know that it's not constructing some non-convex polyhedron that has convex faces that are mutually intersecting, or that extends outside of a hyperplane, for example.
[...]
[...] Are the angle values from Stella? Is there any way of getting more digits for them? [...]
[...]
The values are from Stella, and they are, I presume, rounded to six digits. But the exact values are actually not that important -- you can probably get more precise results by building the solids yourself. What's really important is the algebraic relations between different values (I noted this where I could) and situations where multiple solids share the same angle. For example, you notice that all snubs (including snub disphenoid and snub square antiprism) have completely unique values not related to anything else, coronas are also a world of their own, while bilunabirotunda and triangular hebesphenorotunda are actually related to the "more normal" solids.
Good point.
Hmm, I wonder if there's some way to prove that "unique" angles, say for the snub disphenoid, snub square antiprism, etc., cannot possibly be obtained from any dichoral angle between cells that only have the more "normal" angles? Some sort of algebraic independence theorem that we can use, perhaps? I'm thinking about the similarity between proving that square roots of unrelated non-square numbers cannot possibly be a linear combination of each other; in the geometric world, maybe there are analogous theorems that folding two polyhedra with "strange" angles around a face cannot produce dihedral angles around the face that can fit both "normal" and "unique" polyhedra?
The values, however, should definitely be exact enough to allow for decisions which edges are possible.
I guess next step would be to enumerate the edges?
I wonder if it will be better to have the program automatically enumerate these things, because for the algo to work, it needs to have polyhedron face adjacency data (so that after fitting in a new cell it knows which faces to look at next), and each angle for a given polygon-polygon combination in the lookup table needs to be linked to a precise edge/orientation on the polyhedron. Manually constructing these tables would be too tedious and error-prone, I think. Perhaps the best way is to just construct accurate coordinates for the CRF polyhedra, and then run it through a convex-hull algorithm to generate the face lattice for them; then the CRF search program just loads this data and constructs the requisite internal tables.
I imagine that the key part of the generator will be sieve to eliminate all CRF polychora that were already discovered

Yeah, that is a problem that I've been thinking about. It's a tough one. Basically it's the face lattice isomorphism problem, which according to
this paper is generally as hard as the graph isomorphism problem, which is in NP (requires exponential time algo). Fortunately, it seems that if we bound the number of dimensions (in this case d=4), a polynomial time algorithm is possible.
Johnson solids are classified pretty well; I suspect CRF polychora will have two lists: raw list ordered, say by number of vertices -> edges -> faces -> cells, and then "taxonomic" list where we'll try to fit them.
I've actually thought a lot about classification of CRF polychora following the classification of the Johnson solids. I haven't finalized the full classification scheme yet, but basically we can break it down as follows:
I. Monostratic polychora (includes the Klitzing segmentotopes, but generalized to admit stuff that doesn't inscribe a 3-sphere -- note that Klitzing's list doesn't include things like the snub disphenoid prism because it doesn't inscribe a 3-sphere, so there does remain more monostratic CRFs to be discovered).
II. Laminochora (made by stacking monostratic polychora on top of each other)
III. Rotundae (basically cup-shaped objects with a large cell on the bottom and a small cell/face/edge/vertex on the top, that aren't listed in I and II), and their augmentations with monostratic polychora or laminochora. Maybe diminishings as well, if those aren't already covered.
IV. Modified uniform polychora: diminishings and augmentations with I, II, and/or III. This category includes the duoprisms and their modifications. I've recently started to search for maximally-diminished uniforms, and found a few interesting shapes that aren't in categories I-III, derived from the 5-cell and tesseract families. Currently just starting with the 24-cell family, which promises to have a few interesting cases as well.
V. Crown jewels: stuff that can't be directly derived from the above categories.
There may be more simple categories that I missed, that shouldn't be put in the crown jewels category. As far as I know, we don't know any crown jewels yet. I also don't know how to search academic research papers for them, because of the lack of a common keyword for them (we're the only ones who call them crown jewels AFAIK).
Also, recently I realized that the duoprisms can be augmented not just by prism pyramids (which restricts consideration of duoprisms to those with trigonal, square, pentagonal prism cells), but that for each m,n-duoprism augmented with an m-gonal prism pyramid, there is a corresponding augmentation of a 2m,n-duoprism with an m-gonal cupola (i.e., m-gon||2m-prism). This means that in addition to the 1600+ augmentations of 3,n-duoprisms, 4,n-duoprisms, and 5,n-duoprisms, we also have augmentations of 6,n-duoprims, 8,n-duoprisms, and 10,n-duoprisms, which is at least another 1600+ augmentations, probably much more because the m-gonal cupola induce a symmetry-breaking orientation on the 2n,m-duoprism, which means many more unique combinations. Also, there are more unique positions to augment in a 8,n-duoprism than the 4,n-duoprism (choice from 8 positions instead of just 4, to place the augment).
Also, I imagine that the 7- and 9- prisms and antiprisms will actually have a huge part in the program: if our hypothesis that no new CRF polychora that use them exist, apart from infinite families and augmented duoprisms, is correct, then any new CRF that contains one of these will also have a "twin" containing the other, which could show as a hint to new infinite families. And if one is found without a twin, then our hypothesis was wrong

True!
Marek14 wrote:Further note: I think we should start with just a "proof of concept" program with limited selection of shapes, then extend it.
Good idea, I was thinking the same thing. This goes along with what I said above, that we should precompute the face lattice of all the 3D CRFs, and then the program can just load them (for the initial trial run, we can select a limited subset of them), automatically precompute the tables, etc., and then run the search algo. For testing purposes, we can place an upper limit on cell count, so that the program won't spend huge amounts of time cranking out things like 600-cell diminishings -- those can be temporarily rejected by the upper limit, so that the program will discover smaller interesting CRFs first. Later, once we're confident with the algo, we can let it loose on the full set of 3D CRFs and see what turns up.

Edges with more than 3 cells might present a problem because they are not "rigid" -- 3-cell edge has strictly defined dichoral angles, but 4-cell and more do not (like 4- or more- polygon vertices: compare octahedron's, triangular dipyramid's and pentagonal dipyramid's 4-triangle vertices).
Hmm, you're right! In fact, I've used this very fact to understand how the snub disphenoid can be made from conjoining two octahedra: first you cut off a quadrant from each octahedron, then squeeze them so that the skew polygon around the cut becomes identical to itself rotated 90° then flipped; then you can glue the two 3/4 octahedra together and the result is a snub disphenoid. I tried to discover a similar construction in 4D, but cuttings of the 16-cell produce a skew octahedron at the cut, which can't be made equal to itself with the 90° rotation trick, so you can't glue two 3/4 16-cells this way. So no luck in that direction at producing a crown jewel so far.
In any case, this is bad news for the algorithm.

This means it's only feasible when restricted to 3 cells per edge. Non-rigid edges will greatly increase the complexity of the problem, and may even make it incrementally unsolvable because we may not be able to fix any angles until most of the rest of the shape is constructed. Unfortunately, this also appears to be where a lot of crown jewels are likely to be -- look at the snub disphenoid, for example. It has vertices with 4 triangles that are distorted from the octahedral angles. And the various coronas, which have dihedral angles slightly shifted from the "normal" angles in the platonic solids.
I imagine the end product of the search would be a database with a program attached to search through it, for example by specifying cells which you want/don't want to be present.
Well, assuming we fix a way of canonicalizing CRFs (see face lattice isomorphism above), we can simply have a central database to which we can add newly discovered CRFs. The database will then act as a "canonical listing" of CRFs, perhaps with a front-end that we can use to name/classify the various discovered CRFs. Separating the database from the search program also lets us do incremental searches, e.g., search for CRFs constructed from different subsets of 3D CRFs. It also lets us do SETI-like distributed brute force searches.

This is just my hunch, but I think that the number of anomalous CRF polychora (not related to any uniform) will be bigger then in 3D because there's just significantly more shapes that can be reasonably used. I'm not sure if any are known...
Yeah I don't know of any crown jewels so far.
BTW I found this
interesting page that explains how some of the Johnson "crown jewels" are actually members of a series of mainly-nonconvex polyhedra that just happen to be convex. I wonder if some of the 4D crown jewels will turn out to be convex members of similar series, too.
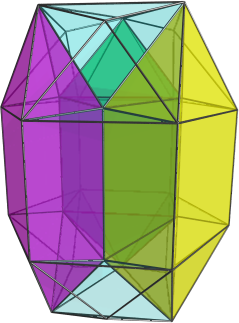



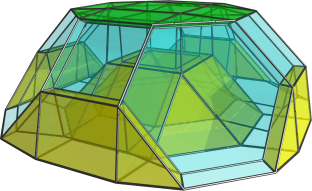
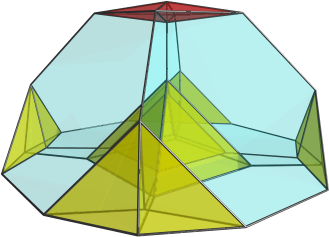

 Well, I hope somebody's reading, 'cos I've discovered a new non-trivial CRF! Here is a projection of it:
Well, I hope somebody's reading, 'cos I've discovered a new non-trivial CRF! Here is a projection of it:
 Oh well. I have nowhere else to post this, so might as well put it here. Maybe someday, somebody will take notice.
Oh well. I have nowhere else to post this, so might as well put it here. Maybe someday, somebody will take notice. 
 Thanks for the off files
Thanks for the off files 

