Johnsonian Polytopes
Johnsonian Polytopes
I've recently been searching for "Johnsonian Polytopes" (only polychora atm)
Defined as:
1) Strictly-Convex from body to cell
(all the elements from body to cell are Strictly-convex: Convex and all it's angles between facets <180 degrees)
2) Non-Vertex-Transitive
(it's not transitive about it's vertices)
3) Regular Faced
(all it's faces are regular polygona)
I've found about 193 so far and was wondering if anyone would be interested in helping me.
(this definition and name is not official)
Defined as:
1) Strictly-Convex from body to cell
(all the elements from body to cell are Strictly-convex: Convex and all it's angles between facets <180 degrees)
2) Non-Vertex-Transitive
(it's not transitive about it's vertices)
3) Regular Faced
(all it's faces are regular polygona)
I've found about 193 so far and was wondering if anyone would be interested in helping me.
(this definition and name is not official)
- wintersolstice
- Trionian
- Posts: 91
- Joined: Sun Aug 16, 2009 11:59 am
Re: Johnsonian Polytopes
What exactly do you mean by strictly convex? If all the angles are <180 degrees then you can't have any lines or planes in your shape. 
I was reading the wikipedia article on vertex transitive graphs and I realised I've forgotten everything I know about group theory, and I never knew much about graph theory .
.
It sounds cool anyway. What sort of shapes have you found so far?

I was reading the wikipedia article on vertex transitive graphs and I realised I've forgotten everything I know about group theory, and I never knew much about graph theory
 .
.It sounds cool anyway. What sort of shapes have you found so far?
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Johnsonian Polytopes
Convex implies that angles are below 180 degrees. "Convex" does not mean "non-self-intersecting".
Sounds like your "Johnsonian Polytopes" are the same shapes FLD can describe.
Sounds like your "Johnsonian Polytopes" are the same shapes FLD can describe.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
PWrong wrote:What exactly do you mean by strictly convex? If all the angles are <180 degrees then you can't have any lines or planes in your shape.
It sounds cool anyway. What sort of shapes have you found so far?
21 pyramids, dipyramids, elongated pyramids and elongated dipyramids of 21 polyhedra
92 prisms of the "Johnson solids" (these shapes are based on them)
augmented tesseracts
and a few more
- wintersolstice
- Trionian
- Posts: 91
- Joined: Sun Aug 16, 2009 11:59 am
Re: Johnsonian Polytopes
wintersolstice wrote:Can I ask a question about your comment?
How can a shape be convex but self-intersecting?
And I thought convex meant the angles were "less than or equal than 180 degrees" (given that all the diagonals lie within the shape)
These shapes are based on the "Johnson solids"
"Johnsonian" was an name suggested by Bowers, I spoke to him about these shapes. And he seemed to understand the definition I created.
thanks (and sorry if I've upset you!)
Oh my, please don't go sending things that are meant to be forum posts in PMs.
A shape can't be both convex and self-intersecting, but it can be neither. Thus merely saying that a shape is non-self-intersecting does not necessarily mean it is convex.
Also I don't see why any convex polytope would have an 180 degree angle anywhere (that wasn't just an arbitrary point inside a facet).
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
I was going by the definition of a strictly convex space. I guess a strictly convex polytope is different.
I still have no idea what vertex transitive means
I still have no idea what vertex transitive means

-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Johnsonian Polytopes
Vertex-transitive means that you can pick any two vertices in the shape, and the facets joined to them will all be equivalent. So a cuboctahedron for example is vertex-transitive because on every vertex there are 2 triangles and 2 squares.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Well I read about "Johnson solids" and they were described as "strictly-convex" and I made a deduction about what it meant
But it's not important.
Anyway they're the 4D analog of Johnson solids if anyone wants to look them up
But it's not important.
Anyway they're the 4D analog of Johnson solids if anyone wants to look them up

- wintersolstice
- Trionian
- Posts: 91
- Joined: Sun Aug 16, 2009 11:59 am
Re: Johnsonian Polytopes
Ok I'm a bit confused. The wiki article says that a square pyramid ad a pentagonal pyramid are Johnson solids, but not a hexagonal pyramid. Surely none of these are vertex transitive?
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Johnsonian Polytopes
A Johnson polyhedron is made of regular polygons, and is convex, but is not elsewhere included in platonic/uniform/etc.
The current thinking of uniform is equal edge + vertex transitive + uniform surtopes.
The hexagonal pyramid, or the hexagonal
Uniform johnson polychora, for example, would be all convex polychora made of regular polygons, except for the sixty-seven regulars, and their classes.
There are of course, the 92 prisms of the three-dimensional ones.
One might here include joys like xo3of3ox, a polytope made of 4 tri-diminished icosahedra, five tetrahedra, and an octahedron, the various diminished 500chora, the various augmented tesseracts (which are indeed convex, giving diminished, or all of the segmentotopes enumerated by Richard Klitzing (eg cube || icosahedron), and various sectionings of the 500ch.
Beside this, there are the figures like point | x-diminished icosa | x-diminished icosa | point, and all various sections thereof, for which gives at least four separate figures.
The current thinking of uniform is equal edge + vertex transitive + uniform surtopes.
The hexagonal pyramid, or the hexagonal
Uniform johnson polychora, for example, would be all convex polychora made of regular polygons, except for the sixty-seven regulars, and their classes.
There are of course, the 92 prisms of the three-dimensional ones.
One might here include joys like xo3of3ox, a polytope made of 4 tri-diminished icosahedra, five tetrahedra, and an octahedron, the various diminished 500chora, the various augmented tesseracts (which are indeed convex, giving diminished, or all of the segmentotopes enumerated by Richard Klitzing (eg cube || icosahedron), and various sectionings of the 500ch.
Beside this, there are the figures like point | x-diminished icosa | x-diminished icosa | point, and all various sections thereof, for which gives at least four separate figures.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Johnsonian Polytopes
Ok I'm a bit confused. The wiki article says that a square pyramid ad a pentagonal pyramid are Johnson solids, but not a hexagonal pyramid. Surely none of these are vertex transitive?
Johnson solids need regular faces, but need not be vertex-transitive. The square and pentagonal pyramids can have regular triangular faces on them, but the hexagonal pyramid cannot because the dihedral angle would be zero, which would make it degenerate. Then it's obvious why n-gonal pyramids with n > 6 are not Johnson solids.
Back to the original point of this topic...
wintersolstice wrote:I've found about 193 so far and was wondering if anyone would be interested in helping me.
Could you list those 193?
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Keijj wrote:Could you list those 193?
I'll have go!
(Elongated)
Tetrahedron, octahedron, icosahedron, cube, triangular prism, pentagonal prism, square antiprism, pentagonal antiprism, snub disphenoid, (bi)(tri) augmented triangular prism, gyroelongated square (di) pyramid, (metabi)(tri) diminished icosahedon, square pyramid, pentagonal (di) pyramid
(di)pyramid
excluding tetrahedron pyramid (regular pentachoron) and octahedron dipyramid (regular hexadecachoron)
82 in total
92 prisms of the Johnson solids
(Parabi) diminished hexacosichoron (2 shapes)(incomplete list)
ortho/gyrobi cube cupola
elongated cube gyrobicupola (gyrate sidpith)
cube cupola
elongated cube cupola (diminished sidpith)
the others are various augmented tesseracts (incomplete list and some don't have names yet)
I hope I've descibed them well enough

- wintersolstice
- Trionian
- Posts: 91
- Joined: Sun Aug 16, 2009 11:59 am
Re: Johnsonian Polytopes
I'll have a go at explaining "Strictly convex" Some shapes have facets that lie in the same subplane but instead of joining them together to make a single facet they're kept as seperate facets. I think you call this "co-planar" some polychora have co-planar facets. A convex shape which is not co-planar is called "strictly convex"
I hope that explains it.
Edit: I've just realised if a 4D+ shape is coplanar then it's facets can be joined and it could still have regular faces so it would still be "strictly convex" so only the cells have to be strictly convex.
I hope that explains it.
Edit: I've just realised if a 4D+ shape is coplanar then it's facets can be joined and it could still have regular faces so it would still be "strictly convex" so only the cells have to be strictly convex.
- wintersolstice
- Trionian
- Posts: 91
- Joined: Sun Aug 16, 2009 11:59 am
Re: Johnsonian Polytopes
I get the idea of strictly convex now, thanks.
It's an impressive list, do you think there are many more? How did you go about counting the ones you've found?
It's an impressive list, do you think there are many more? How did you go about counting the ones you've found?
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Johnsonian Polytopes
A large number of the Johnson polyhedra are laminate: that is, one can build them by placing successive layers like pyramid+prism+pyramid. We (Richard Klitzing and myself), devised a notion for forming notations, that represent more polytopes by means of "layers of dynkin symbols". For example, the general antiprism, might be considered as xPo || oPx (meaning, xPo on top, and oPx), or xoPox, which represents an array, the n_th layer is represented by layer n.
The tri-diminished dodecahedron, then might be x3o || f3o || o3x, which becomes xfo3oox&#t. (See eg Lace towers in my Polygloss). This occurs as a face of a four-dimensional polytope xf3oox3ooo&#t, a figure bounded by four tri-diminished icosahedra, five tetrahedra, and an octahedron.
Google on Klitzing Segmentotopes , and ye will find a number of interesting things that will help you. Klitzing enumerated the segmentotopes, being polytopes of equal edge, for which all vertices lie in two parallel rings of a sphere. The .pdf file corresponds to a paper listing some 184 segmentatopes or so, many of these are Johnson polychora.
One of the more interesting figures by Klitzing is "cube || icosahedron". The axial symmetry here is 3*2, or pyritohedral, it occurs in the {3,3,5}, where the cube is part of the dodecahedral layer, and the icosahedron is the large icosahedron layer below the mid-ring.
The next step is that ye can stack these, to get various laminatopes. A useful place to start is something like the 500ch {3,3,5}. Its layers give a fruitful source of johnsons, eg oxoo3ooox5ooxo, a polytope which comprises of several rings of the {3,3,5}, the face consist being tetrahedra, 12 diminished icosahedra, and one icosadodecahedron.
This has four bands, which must occur, and variations of putting a fifth band in, to cater for any of 1-12 apiculations (the diminished icosahedra can have a pyramid mounted on it, replacing this face with tetrahedra and a pentagonal pyramid.
You can mount any consecutive number of these bands together, with an prism layer ("elongated"), with a reversal to any earlier point.
The tri-diminished dodecahedron, then might be x3o || f3o || o3x, which becomes xfo3oox&#t. (See eg Lace towers in my Polygloss). This occurs as a face of a four-dimensional polytope xf3oox3ooo&#t, a figure bounded by four tri-diminished icosahedra, five tetrahedra, and an octahedron.
Google on Klitzing Segmentotopes , and ye will find a number of interesting things that will help you. Klitzing enumerated the segmentotopes, being polytopes of equal edge, for which all vertices lie in two parallel rings of a sphere. The .pdf file corresponds to a paper listing some 184 segmentatopes or so, many of these are Johnson polychora.
One of the more interesting figures by Klitzing is "cube || icosahedron". The axial symmetry here is 3*2, or pyritohedral, it occurs in the {3,3,5}, where the cube is part of the dodecahedral layer, and the icosahedron is the large icosahedron layer below the mid-ring.
The next step is that ye can stack these, to get various laminatopes. A useful place to start is something like the 500ch {3,3,5}. Its layers give a fruitful source of johnsons, eg oxoo3ooox5ooxo, a polytope which comprises of several rings of the {3,3,5}, the face consist being tetrahedra, 12 diminished icosahedra, and one icosadodecahedron.
This has four bands, which must occur, and variations of putting a fifth band in, to cater for any of 1-12 apiculations (the diminished icosahedra can have a pyramid mounted on it, replacing this face with tetrahedra and a pentagonal pyramid.
You can mount any consecutive number of these bands together, with an prism layer ("elongated"), with a reversal to any earlier point.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Johnsonian Polytopes
Keiji wrote:Vertex-transitive means that you can pick any two vertices in the shape, and the facets joined to them will all be equivalent. So a cuboctahedron for example is vertex-transitive because on every vertex there are 2 triangles and 2 squares.
That is a consequence of transitivity, not the definition; in other words it is a necessary property but not sufficient. The classic counterexample is the pseudorhombicuboctahedron, Johnson #37.
A figure is vertex-transitive if all vertices are equivalent under the figure's isometry group.
- Tamfang
- Dionian
- Posts: 39
- Joined: Sun May 23, 2010 9:06 pm
- Location: Cascadia
Re: Johnsonian Polytopes
As I've derived it, the formation of a 4D cupola is:
|V'| = |V| + Σ∀v∈V[deg(v)]
|E'| = 3|E| + 2Σ∀v∈V[deg(v)]
F' = 2F ∪ (3|E|){4}
C' = Expand*(C) ∪ |V|{3,3} ∪ |E|[{3}×{}] ∪ ⋃∀f∈F[f×{}] ∪ C
Where Expand*(C) is the expanded version of the original polyhedron.
A question: Can any CRF polyhedron (CRF = convex regular-faced; i.e. any Platonic, Archimedean or Johnson solid, or a prism/antiprism), other than the prisms/antiprisms above 5, form a cupola which has regular faces and is therefore Johnsonian?
|V'| = |V| + Σ∀v∈V[deg(v)]
|E'| = 3|E| + 2Σ∀v∈V[deg(v)]
F' = 2F ∪ (3|E|){4}
C' = Expand*(C) ∪ |V|{3,3} ∪ |E|[{3}×{}] ∪ ⋃∀f∈F[f×{}] ∪ C
Where Expand*(C) is the expanded version of the original polyhedron.
A question: Can any CRF polyhedron (CRF = convex regular-faced; i.e. any Platonic, Archimedean or Johnson solid, or a prism/antiprism), other than the prisms/antiprisms above 5, form a cupola which has regular faces and is therefore Johnsonian?
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Two possible CRF ("Johnsonian") polychora:
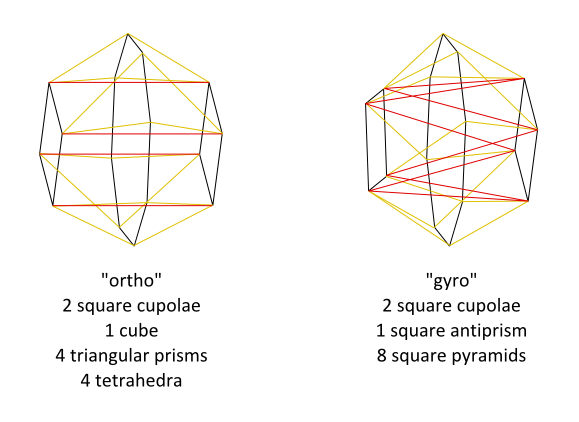
I came up with these while thinking about how a cell could be attached to a rotated copy of itself in 4D.
Both forms have 16 vertices.
The "ortho" form has 36 edges (16 black, 4 red and 16 yellow).
The "gyro" form has 40 edges (16 black, 8 red and 16 yellow).
The "ortho" form has 31 faces (1 octagon, 14 squares and 16 triangles).
The "gyro" form has 35 faces (1 octagon, 10 squares and 24 triangles).
I like how they turned out somewhat like a duoprism (the projections show an "in-out ring" of 2 cupolae and prism/antiprism, and a "round-the-outside ring" of triangular prisms/tetrahedra and square pyramids)
A few questions...
1. are these two shapes indeed CRF polychora? (i.e. can they be built with all their (two-dimensional) faces regular?)
2. do these appear in wintersolstice's list above? IIRC, his list was mainly composed of prismatoid-like forms (3+1) whereas these are more duoprismatic-like forms (2+2)
3. is the "gyro" form the first explicitly constructed polychoron to include the square antiprism as a cell (other than trivial things like the square antiprism prism/pyramid)? if not, what came before it?
4. any name suggestions for these two?
5. could quickfur render them, pretty-please? I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
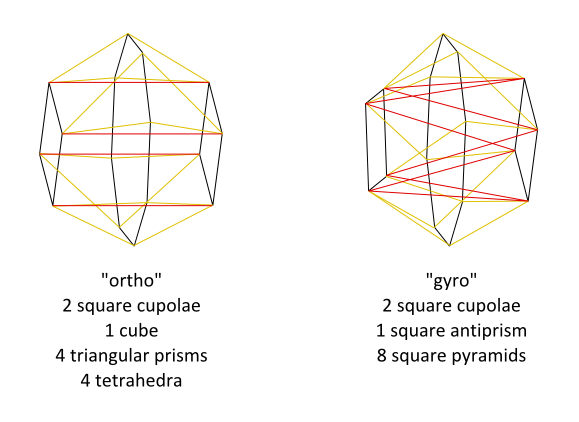
I came up with these while thinking about how a cell could be attached to a rotated copy of itself in 4D.
Both forms have 16 vertices.
The "ortho" form has 36 edges (16 black, 4 red and 16 yellow).
The "gyro" form has 40 edges (16 black, 8 red and 16 yellow).
The "ortho" form has 31 faces (1 octagon, 14 squares and 16 triangles).
The "gyro" form has 35 faces (1 octagon, 10 squares and 24 triangles).
I like how they turned out somewhat like a duoprism (the projections show an "in-out ring" of 2 cupolae and prism/antiprism, and a "round-the-outside ring" of triangular prisms/tetrahedra and square pyramids)
A few questions...
1. are these two shapes indeed CRF polychora? (i.e. can they be built with all their (two-dimensional) faces regular?)
2. do these appear in wintersolstice's list above? IIRC, his list was mainly composed of prismatoid-like forms (3+1) whereas these are more duoprismatic-like forms (2+2)
3. is the "gyro" form the first explicitly constructed polychoron to include the square antiprism as a cell (other than trivial things like the square antiprism prism/pyramid)? if not, what came before it?
4. any name suggestions for these two?

5. could quickfur render them, pretty-please?
 I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Keiji wrote:[...]1. are these two shapes indeed CRF polychora? (i.e. can they be built with all their (two-dimensional) faces regular?)
Yess! And the listed cells are all correct. For the ortho form, basically you take two square cupolae, join them at their octagonal bases, then fold them into 4D and attach a cube at the far end, thus making a triangular circuit of facets. Then the gaps can be filled in with triangular prisms and tetrahedra: all edge lengths are equal so you will have regular ridges.
Similarly for the gyro form, after folding into 4D you use a square antiprism to make the triangular circuit of facets, which will have a different height from the ortho form, but that's OK because the edge lengths are still equal and you'll get square pyramids with equilateral triangles.
2. do these appear in wintersolstice's list above? IIRC, his list was mainly composed of prismatoid-like forms (3+1) whereas these are more duoprismatic-like forms (2+2)
That I don't know.
3. is the "gyro" form the first explicitly constructed polychoron to include the square antiprism as a cell (other than trivial things like the square antiprism prism/pyramid)? if not, what came before it?
I suppose you regard Cartesian products of the square antiprism trivial too?

4. any name suggestions for these two?
That's a hard one. There are so many ways you can attach cells together in 4D, it's hard to think of a name that adequately conveys how this thing is constructed. Are there existing naming conventions for these things, that we can generalize from? (Yes I'm too lazy to actually look it up.
 )
)5. could quickfur render them, pretty-please?
Do you have coordinates for them? I can do it a lot faster if you do.
 Otherwise it may take a while for me to calculate the coordinates.
Otherwise it may take a while for me to calculate the coordinates.I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
Plus you didn't fold the square cupolae enough to make the cube/square antiprism uniform.

But speaking of cupolae... you can actually make native 4D equivalents of cupolae. A year or two ago (or maybe a few more years before that
 ), somebody on Wikipedia had the insight is that the square cupola, for example, can be constructed by starting with a square, then pulling its edges apart radially as you sweep out a 3D volume, until it turns into an octagon. The original square is then the top face of the cupola and the octagon the bottom face, and the original edges sweep out a square while the original vertices are expanded as you drag the shape out, so they form triangles.
), somebody on Wikipedia had the insight is that the square cupola, for example, can be constructed by starting with a square, then pulling its edges apart radially as you sweep out a 3D volume, until it turns into an octagon. The original square is then the top face of the cupola and the octagon the bottom face, and the original edges sweep out a square while the original vertices are expanded as you drag the shape out, so they form triangles.So you can do the same thing for 3D polyhedra: start with a cube, then pull out its faces radially as you sweep it along the 4th direction, until it becomes a rhombicuboctahedron. As you do so, the original square faces trace out cubes, the original edges expand into squares thus forming triangular prisms, and the original vertices form tetrahedra. So you have 1+6=7 cubes, 12 triangular prisms, 8 tetrahedra, and 1 rhombicuboctahedron. This is the cubical cupola.
Doing the same thing to an octahedron gives you a cupola also with a rhombicuboctahedral base, but with slightly different cells: 1 octahedron, 8+12=20 triangular prisms, 6 square pyramids, and 1 rhombicuboctahedron.
And starting with a tetrahedron: 1+4=5 tetrahedra, 4+6=10 triangular prisms, and 1 cuboctahedron. This one is particularly interesting, because if you attach two of these cupolae by their cuboctahedral bases in dual-tetrahedron orientation, you get a runcinated 5-cell. What even more interesting is that this particular cupola belongs to a family of cupola that, when joined by their bases, form n-simplex runcinates (I'm using "runcinate" in the sense of the CD diagrams xoo...oox). Which I have already written about in my runcinated 5-cell page.
Anyway, starting from an icosahedron: 1 icosahedron, 12 pentagonal pyramids, 20+30=50 triangular prisms, and 1 rhombicosidodecahedron.
And starting from a dodecahedron: 1 dodecahedron, 12 pentagonal prisms, 30 triangular prisms, 20 tetrahedra, and 1 rhombicosidodecahedron.
All of these cupola can be attached to another copy of themselves via their bases to form 4D bicupolae; and if you insert a prism of their base in between, you get elongated bicupolae. Not all of them have gyro forms, though; the only one is the tetrahedral cupola (because the cuboctahedron has two different tetrahedral orientations, even though as a cubic truncate it's not self-dual). However, you can attach different cupola with the same base: for example, a cubic cupola can attach to an octahedral cupola to form a cubic-octahedral bicupola, and inserting a rhombicuboctahedral prism gives you a cubic-octahedral elongated bicupola.
Lots of fun to be had with these shapes.

- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
P.S. and all of the cupolae I described can be made to have regular ridges, of course.
- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Coordinates of "ortho" are (±(1+sqrt(2)),±1,0,0), (±1,±(1+sqrt(2)),0,0), (±1,±1,1,±1). For "gyro" it's more difficult, because height of 4-antiprism is a difficult value itself 

- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
quickfur wrote:Keiji wrote:[...]1. are these two shapes indeed CRF polychora? (i.e. can they be built with all their (two-dimensional) faces regular?)
Yess! And the listed cells are all correct.
Hurray!

3. is the "gyro" form the first explicitly constructed polychoron to include the square antiprism as a cell (other than trivial things like the square antiprism prism/pyramid)? if not, what came before it?
I suppose you regard Cartesian products of the square antiprism trivial too?
Of course.
4. any name suggestions for these two?
That's a hard one. There are so many ways you can attach cells together in 4D, it's hard to think of a name that adequately conveys how this thing is constructed. Are there existing naming conventions for these things, that we can generalize from? (Yes I'm too lazy to actually look it up.)
Not that I know of. I do want a name (or series of names, rather) that conveys the duoprismatic and dipyramidal characteristics of these shapes though. There would, of course, be four more of these - triangular ortho, triangular gyro, pentagonal ortho, and pentagonal gyro.
5. could quickfur render them, pretty-please?
Do you have coordinates for them? I can do it a lot faster if you do.Otherwise it may take a while for me to calculate the coordinates.
Sadly not.
You could probably calculate coordinates faster and more accurately than me, though!

(Thank you Mrrl
 You posted those while I was writing my reply.)
You posted those while I was writing my reply.)I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
Plus you didn't fold the square cupolae enough to make the cube/square antiprism uniform.
I wasn't bothered about that one. Stretching the shape is one thing, twisting it is another.
But speaking of cupolae... you can actually make native 4D equivalents of cupolae.
Yep, those are included in wintersolstice's list, and I have read the text on Wikipedia that you mention. These are analogous to the 2->3D cupolae, whereas my objects aren't really cupolae at all, they just include them as facets! To me, the 3->4D cupolae are more basic, like making a prism or pyramid, while these shapes are more interesting, since the operation is done on a polygon to directly build a 4D shape (in the same way that duoprisms and the duocylinder and tiger are more interesting than the prisms, cubinder/spherinder and respective torii).
The reason I asked if my shapes were somehow included in his list are that no matter how many times I read it, I don't see them anywhere, but I can't convince myself 100%, because there have been several instances where I've thought two shapes were different until it was made immediately obvious that they were actually the same. For example, I worked out the alternation of the rhombo-hexagonal dodecahedron earlier by drawing it manually, and it took a stupidly long time before I eventually realized that my diagram was just the triaugmented triangular prism turned on its side! And that's just a 3D shape!
Not all of them have gyro forms, though; the only one is the tetrahedral cupola (because the cuboctahedron has two different tetrahedral orientations, even though as a cubic truncate it's not self-dual). However, you can attach different cupola with the same base: for example, a cubic cupola can attach to an octahedral cupola to form a cubic-octahedral bicupola, and inserting a rhombicuboctahedral prism gives you a cubic-octahedral elongated bicupola.
Indeed, I would call the cube-octahedron and icosahedron-dodecahedron bicupolae gyro forms though, because they are bicupolae of a pair of duals - just like the tetrahedral gyrobicupola is of a pair of duals (two tetrahedra in dual orientations), and so are the n-gonal cupolae.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Keiji wrote:[...]
Indeed, I would call the cube-octahedron and icosahedron-dodecahedron bicupolae gyro forms though, because they are bicupolae of a pair of duals - just like the tetrahedral gyrobicupola is of a pair of duals (two tetrahedra in dual orientations), and so are the n-gonal cupolae.
You're right, perhaps "gyro" is a bit misleading, since you think of merely rotating the base shapes, but what we're doing here is using duals to fit two cupolae together.
On another note, does wintersolstice's list include the polyhedron-dual pseudo-antiprisms? OK i've no idea what they're called, but basically you start with a polyhedron, then truncate it into its dual while sweeping out a 4D volume. The resulting shape has the polyhedron at one end and its dual at the other end, with various pyramids connecting them.
So a cube-octahedron pseudo-antiprism consists of a cube, an octahedron, 6 square pyramids, and 8 tetrahedra.
The tetrahedron-tetrahedron pseudo-antiprism happens to be the same as the 16-cell, interestingly enough.
The icosahedron-dodecahedron pseudo-antiprism consists of an icosahedron, a dodecahedron, 12 pentagonal pyramids and 20 tetrahedra.
On yet another note, here's a slight variation on your new CRF polytopes: start with 2 square cupola as before, but instead of joining them base-to-base, insert an octagonal prism between them, and fold them up so that their top square faces connect. If you insert a cube between the square faces instead, you get the prism of the square cupola, but here we're omitting the cube. So it's sorta like a "reverse" form of your ortho- form.
Unfortunately there is no gyro form since the faces won't line up.
- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Lots of Johnsonian polychora are Richard Klitzing segmentotopes (defined as polychora with regular 2-faces squeezed between two parallel planes). They are good building blocks as well 

- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Looks like there is 12-vertex polychoron with two 4-antiprism cells: you take two 4-antiprisms, one cube and form a tube from them (connecting them by square faces). Then close it with another tube of 4 tetrahedra and 4 square pyramids. So it's a kind of skew {4,3} douprism. All edges may be made equal in this object.
Last edited by Mrrl on Mon Nov 21, 2011 10:55 pm, edited 1 time in total.
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Johnsonian Polytopes
wintersolstice's list contains exhaustively:
* prisms of Johnson solids
* (elongated) (bi)pyramids of CRF polyhedra - four forms per polyhedron, excluding two cases which overlap with uniform polychora
* seven explicitly named shapes:
** cubic cupola
** elongated cubic cupola (diminished sidpith)
** cubic orthobicupola
** cubic gyrobicupola
** elongated cubic gyrobicupola (gyrate sidpith)
** diminished hexacosichoron
** parabidiminished hexacosichoron
* "various augmented tesseracts", whatever they might be.
My question of whether my polychora were included in his list is more a question of whether they "accidentally" happen to overlap with something of a simpler construction which would be in that list, like how the two mentioned cases overlap with particular uniform polychora.
I would imagine that your "pseudo-antiprisms" (which I would just call antiprisms, for the same reason as calling the dual-based bicupolae gyro- even though you're doing more than just rotating them) are not in that list.
Would a "square pyramid antiprism" (note that 2->3D pyramids are self-dual) overlap? I have a feeling it may overlap with something containing an octahedron, but I'm not sure, mainly because I haven't bothered to calculate the facets of such an antiprism (yet).
As for the "reverse ortho" form, I like it Perhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".
Perhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".
* prisms of Johnson solids
* (elongated) (bi)pyramids of CRF polyhedra - four forms per polyhedron, excluding two cases which overlap with uniform polychora
* seven explicitly named shapes:
** cubic cupola
** elongated cubic cupola (diminished sidpith)
** cubic orthobicupola
** cubic gyrobicupola
** elongated cubic gyrobicupola (gyrate sidpith)
** diminished hexacosichoron
** parabidiminished hexacosichoron
* "various augmented tesseracts", whatever they might be.
My question of whether my polychora were included in his list is more a question of whether they "accidentally" happen to overlap with something of a simpler construction which would be in that list, like how the two mentioned cases overlap with particular uniform polychora.
I would imagine that your "pseudo-antiprisms" (which I would just call antiprisms, for the same reason as calling the dual-based bicupolae gyro- even though you're doing more than just rotating them) are not in that list.
Would a "square pyramid antiprism" (note that 2->3D pyramids are self-dual) overlap? I have a feeling it may overlap with something containing an octahedron, but I'm not sure, mainly because I haven't bothered to calculate the facets of such an antiprism (yet).
As for the "reverse ortho" form, I like it
 Perhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".
Perhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Johnsonian Polytopes
Mrrl wrote:Looks like there is 12-vertex polychoron with two 4-antiprism cells: you take two 4-antiprisms, one cube and form a tube from them (connecting them by square faces). Then close it with another tube of 4 tetrahedra and 4 square pyramids. So it's a kind of skew {4,3} douprism. All edges may be made equal in this object.
As far as I know, this is also a valid CRF polychoron. It's possible to make all edges equal length, so all polygonal ridges will be regular.
I just thought of another polychoron with square antiprisms: this one has 4 square antiprisms, so it's non-trivial.
 Basically, take 4 of these antiprisms and join them together by their square faces, then fold them up to form a 4-membered ring in 4D. If I'm not wrong, you should be able to fill in the gaps with tetrahedra and square pyramids. I think all edge lengths should be equal, so this should be a CRF polychoron too. I'm still trying to figure out how many tetrahedra/pyramids are needed to close up the shape.
Basically, take 4 of these antiprisms and join them together by their square faces, then fold them up to form a 4-membered ring in 4D. If I'm not wrong, you should be able to fill in the gaps with tetrahedra and square pyramids. I think all edge lengths should be equal, so this should be a CRF polychoron too. I'm still trying to figure out how many tetrahedra/pyramids are needed to close up the shape.- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Another class of shapes should be doable by cutting vertices from icositetrachoron. You can cut a vertex and replace it by a cube, cutting six octahedra in half so they become square pyramids, right?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Keiji wrote:[...]
* "various augmented tesseracts", whatever they might be.
If the name is anything to go by, I'd imagine it's attaching 1 to 8 cubical pyramids to the tesseract's surface. Attaching 8 pyramids would, of course, turn it into a 24-cell; if any one of them are missing, you'll get a kind of truncated 24-cell (not to be confused with the uniform polychoron called truncated 24-cell, but a 24-cell from which a cubical pyramid has been cut off). And because pyramids on adjacent faces produce regular octahedral facets in addition to square pyramids, you can "pyramidize" any subset of the tesseract's facets and still get a convex CRF shape.
My question of whether my polychora were included in his list is more a question of whether they "accidentally" happen to overlap with something of a simpler construction which would be in that list, like how the two mentioned cases overlap with particular uniform polychora.
I see.
I would imagine that your "pseudo-antiprisms" (which I would just call antiprisms, for the same reason as calling the dual-based bicupolae gyro- even though you're doing more than just rotating them) are not in that list.
I would like to call them antiprisms too, except that due to the multiple derivations of 3D antiprisms, the term is kinda ambiguous. Some people would consider alternated 2n,2n-duoprisms as the 4D analogues of antiprisms, for example, even though most of them are not uniform. Then there's the "grand antiprism" which isn't really an antiprism, though it is somewhat analogous in the sense of having a sheet of tetrahedra between its two rings of antiprisms (analogous to a ring of triangles between two polygons in 3D antiprisms).
Then there's the direct analogue of sweeping out a 3D volume while truncating a polygon to its dual, the only problem being that most people don't think of the 3D antiprisms as being constructed in this way.
Would a "square pyramid antiprism" (note that 2->3D pyramids are self-dual) overlap? I have a feeling it may overlap with something containing an octahedron, but I'm not sure, mainly because I haven't bothered to calculate the facets of such an antiprism (yet).
Hmm, this is an interesting one. A square pyramid antiprism would have 4 square pyramids and 4+4=8 tetrahedra. However, I suspect that these are not regular tetrahedra, because 4 of them arise from truncating the corners of the square pyramid, and the vertex figure there is not equilateral.
As for the "reverse ortho" form, I like itPerhaps it should be called magna-something (in place of ortho/gyro-something), since we are inserting a larger polytope (octahedral prism as opposed to square (anti)prism), and magna is Latin for "great".
Hmm. I'm not sure either way... the name sounds cool but I'm not sure if it will fit well in the grand scheme of things.
But that calls for ... the initiation of the Johnsonian Polychora Project! We need a project to discover all 4D johnsonian polychora and classify them. Do I hear a cheer? I'm guessing we have volunteers here?

- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Marek14 wrote:Another class of shapes should be doable by cutting vertices from icositetrachoron. You can cut a vertex and replace it by a cube, cutting six octahedra in half so they become square pyramids, right?
I would imagine this would be the same as the "augmented tesseracts", if that name means what I think it means.
- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Who is online
Users browsing this forum: No registered users and 34 guests
