
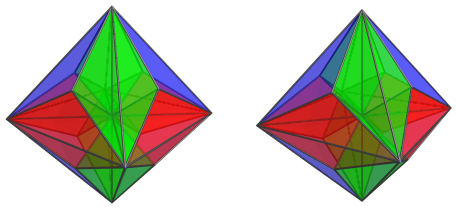
This is what the Polytope Wiki calls the Triangular Antitegmatic Hexacontatetrachoron, the dual of the runcinated tesseract. It's obviously the direct analogue of the deltoidal icositetrahedron, the dual of the rhombicuboctahedron.
Interestingly enough, the projection envelope of this 4D baby is exactly the deltoidal icositetrahedron, having exactly the same proportions. This leads to a conjecture that all duals of x4o...o3x have this projective relationship with each other. I haven't worked out the proof yet, nor have I checked the 5D analogue yet, but I'm fairly confident this is the case. I find this remarkable, because most of the 4D Catalans (that I've checked so far) don't have such direct proportions with their 3D analogues. It seems that x4o...o3x is one of those cases where there's a direct analogy across dimensions -- if this conjecture is true. It's also remarkable that this polychoron has 3 different edge lengths, whereas the deltoidal icositetrahedron has only 2 different edge lengths, yet in the projection the edge length proportions line up nicely. So this projective relationship isn't as trivial as it may seem. In any case, it's an interesting observation.

 I'll get around to it sometime today, hopefully.
I'll get around to it sometime today, hopefully.






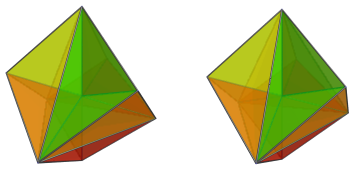








![Pleased :]](./images/smilies/pleased.gif) ), it looks like you're using just one of the colours, not combining them. Specifically, if both chora are visible, then the hedron gets the colour of the one farther from the 3D viewpoint. I think I used this method for some of my images.
), it looks like you're using just one of the colours, not combining them. Specifically, if both chora are visible, then the hedron gets the colour of the one farther from the 3D viewpoint. I think I used this method for some of my images.